Generative Adversarial Networks

敵対的生成ネットワーク(GANs)の導入

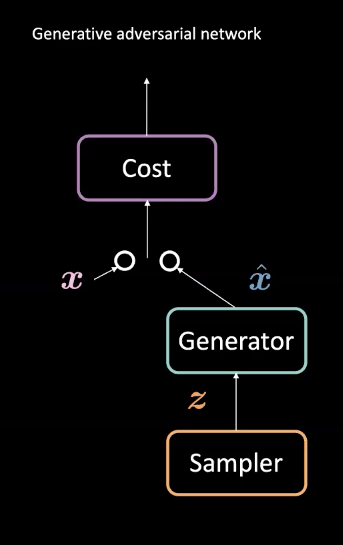
図1: GANのアーキテクチャ

GANは教師なし機械学習に使用されるニューラルネットワークの一種です。GANは2つの敵対的なモジュールで構成されています。generator ネットワークと　cost ネットワークです。cost　ネットワークが偽の例をフィルタリングしようとするのに対し、generator　は現実的な例を作ることでこのフィルタを騙そうとすることで、これらのモジュールは互いに競合します。この競争を通じて、モデルは現実的なデータを生成する生成器を学習します。将来予測や、特定のデータセットで訓練された後の画像生成などのタスクで使用することができます。

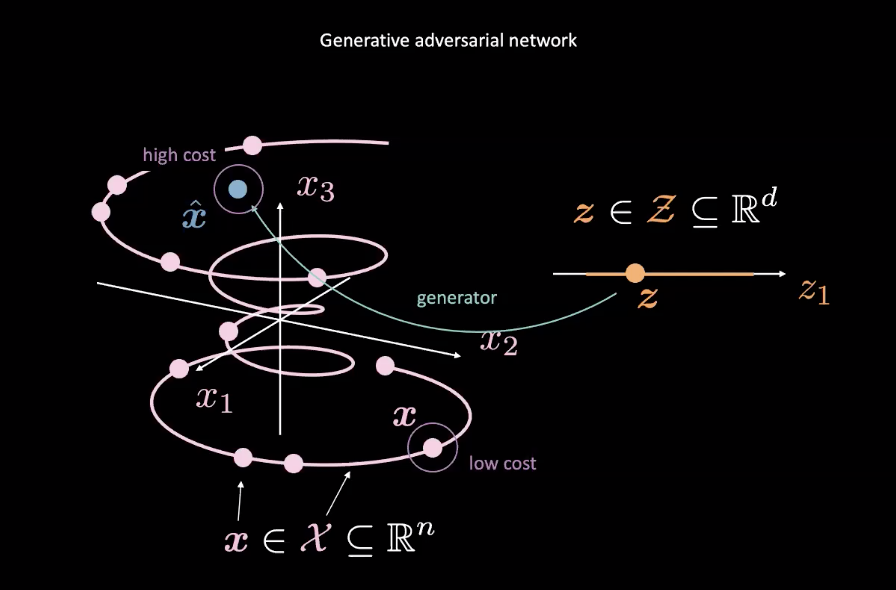
図2: ランダム変数からのGANの写像

GAN はエネルギーベースモデル（EBM）の一例です。したがって、コストネットワークは、図２のピンクの $\vect{x}$ で示される真のデータ分布に近い入力に対して低いコストを出力するように訓練されます。図２の青い $\vect{\hat{x}}$ のような他の分布からのデータは、高いコストを持たなければいけません。コストネットワークの性能を計算するために、一般的に平均二乗誤差（MSE）が使用されます。ここで注目すべきは、コスト関数が、指定された範囲内で正のスカラー値を出力することです（例えば$\text{cost} : \mathbb{R}^n \rightarrow \mathbb{R}^+ \cup {0}$）。これは、離散的な分類結果を出力に用いる通常の識別器とは異なります。

一方、生成器（$\text{generator} : \mathcal{Z} \rightarrow \mathbb{R}^n$）は、ランダムな変数$\vect{z}$から、コストネットワークを騙すための本物のようなデータ$\vect{\hat{x}}$への写像を改善するように、訓練されます。生成器は、コストネットワークの出力について、$\vect{\hat{x}}$のエネルギーを最小にするように学習します。このエネルギーを$C(G(\vect{z}))$と呼びますが、ここでは、$C(\cdot)$がコストネットワーク、$G(\cdot)$が生成ネットワークです。

コストネットワークの訓練は、MSE損失を最小化することを基本とし、生成ネットワークの訓練は、$\vect{\hat{x}}$についての$C(\vect{\hat{x}})$の勾配を用いて、コストネットワークを最小化することで行います。

データ多様体の外側の点に対してはコストが高く、内側の点に対してはコストが低くなるように、コストネットワークの損失関数 $\mathcal{L}{C}$ は、ある正のマージン$m$に対して $C(x)+[m-C(G(\vect{z}))]^+$となります。$\mathcal{L}{C}$を最小化するためには、$C(\vect{x}) \rightarrow 0$であり$C(G(\vect{z})) \rightarrow m$であることが必要です。生成器の損失$\mathcal{L}_{G}$は単純に $C(G(\vect{z}))$ であり、これは生成器が確実に $C(G(\vect{z})) \rightarrow 0$ となるように促します。 しかし、これは $0 \leftarrow C(G(\vect{z})) \rightarrow m$ のように不安定になります。

GANとVAEの違い

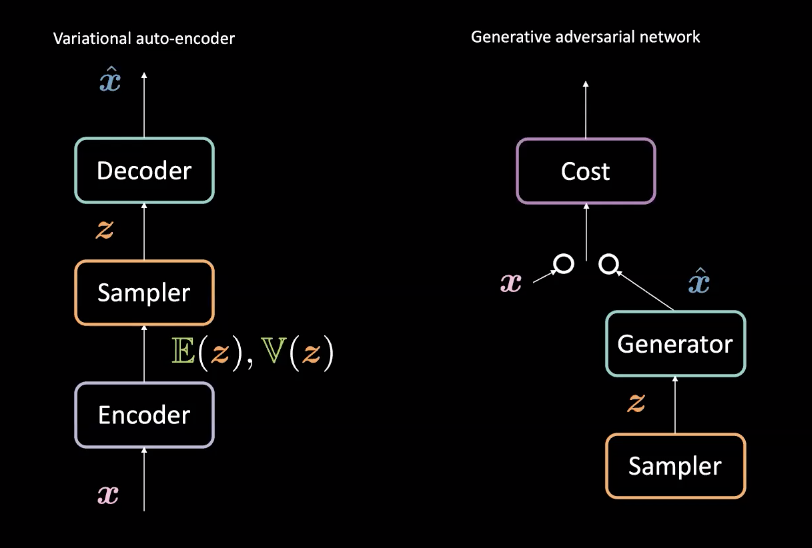
図3: VAE (左) vs. GAN (右) - アーキテクチャのデザイン

第８週の変分オートエンコーダー(VAE)と比較して、GANはジェネレーターの作成方法が少し異なります。VAEは、encoder　で入力$\vect{x}$を潜在空間$\mathcal{Z}$に写像し、　decoder　で$\mathcal{Z}$からデータ空間に写像することで、$\vect{\hat{x}}$を得るのでした。そして、再構成誤差を利用して、$\vect{x}$と$\vect{\hat{x}}$を似たようなものにしていました。一方、GANは、上述したように、生成ネットワークとコストネットワークが競合する敵対的な設定で訓練を行います。これらのネットワークは、勾配に基づいた手法を用いて誤差逆伝播を行いながら学習します。このアーキテクチャの違いを比較すると、図3のようになります。

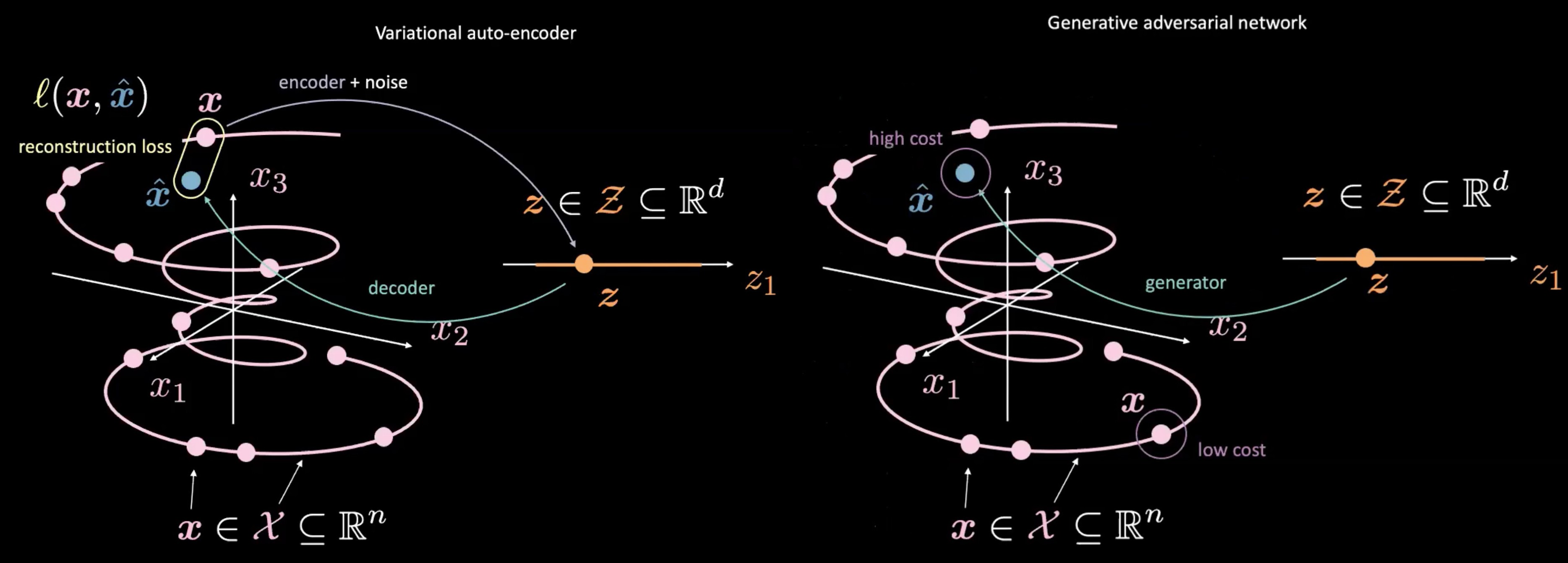
図4: VAE (左) vs GAN (右) - ランダムサンプル $\vect{z}$からの写像

また、どのように生成を行い、どのように$\vect{z}$を使用するかという点で、GANとVAEは異なります。VAEの潜在空間で行われるのと同様に、GANではまず$\vect{z}$をサンプリングします。次に、生成ネットワークを用いて、$\vect{z}$を$\vect{\hat{x}}$に写像します。この$\vect{\hat{x}}$は、それがどれだけ「本物」であるかを評価するために、識別器/コストネットワークに入力されます。VAEとGANの主な違いの一つは、GANでは生成ネットワークの出力と実データとの間の直接的な関係（再構成誤差）を測定する必要がないことです。 その代わりに、我々は、識別器/コストネットワークが本物のデータ$\vectct{x}$と似たようなスコアを生成するように生成器を訓練することで、$\vect{\hat{x}}$が$\vect{x}$と似たようなものになるように強制します。

GANの主な落とし穴

GANは生成器の構築に威力を発揮しますが、いくつかの大きな落とし穴があります。

1. 不安定な収束性

生成器が訓練によって改善されるにつれて、識別器の性能は悪くなります。生成器が完全であれば、本物のデータと偽物のデータの多様体は互いに重なり合い、識別器は多くの誤分類を生み出すことになります。

識別器のフィードバックは時間の経過とともに意味をなさなくなりますが、これは、GANの収束に問題をもたらします。GANが、識別器が完全にランダムなフィードバックを与えている時点を超えて学習を続けると、生成器は質の悪いフィードバックで学習を開始し、その品質が崩壊する可能性があります。GANの学習の収束を参照してください。

この生成器と識別器の間の敵対的な性質の結果として、安定ではなく不安定な平衡点が生じます。

2. 勾配消失

GANにバイナリクロスエントロピー損失を使うことを考えてみましょう。

識別器が自信を持つようになると、$D(\vect{x})$は$1$に近づき、$D(\vect{\hat{x}})$は$0$に近づきます。この自身は、コストネットワークの出力を、勾配が飽和するようなより平坦な領域に移動させます。これらの平坦な領域は、生成ネットワークの学習の妨げとなる、勾配消失を引き起こします。したがって、GANを訓練する際には、自信が高まるにつれてコストが徐々に増加するようにしたいという要請が生まれます。

3. モード崩壊

生成器が、サンプラーからのすべての$\vect{z}$を 単一の 識別器を騙すことができる$\vect{\hat{x}}$に写像することができるならば、生成器はそのような$\vect{\hat{x}}$だけを生成することになります。最終的に、識別器は、この偽の入力の検出に特化した学習をしてしまいます。すると、生成器は、次の最も妥当な$\vect{\hat{x}}$を見つけ、そのサイクルを継続してしまいます。その結果、偽の $\vect{\hat{x}}$ を循環させている間に、識別器は局所解に捕らわれてしまいます。この問題の解決策として、異なる入力が与えられたときに、常に同じ値を出力することに何らかのペナルティを課すことが考えられます。

Deep Convolutional Generative Adversarial Network (DCGAN) source code

この例のソースコードはここから見みることができます。

生成器

1. 生成器は、nn.BatchNorm2d と nn.ReLU で区切られた複数の nn.ConvTranspose2d モジュールを用いて入力をアップサンプリングします。
2. 系列の最後に、ネットワークは nn.Tanh() を用いて出力を $(-1,1)$ の範囲にします。
3. 入力であるランダムベクトルのサイズは$nz$で、出力のサイズは$nc \times 64 \times 64$です。ここで$nc$はチャンネル数を表しています。

class Generator(nn.Module):
    def __init__(self):
        super().__init__()
        self.main = nn.Sequential(
            # input is Z, going into a convolution
            nn.ConvTranspose2d(     nz, ngf * 8, 4, 1, 0, bias=False),
            nn.BatchNorm2d(ngf * 8),
            nn.ReLU(True),
            # state size. (ngf*8) x 4 x 4
            nn.ConvTranspose2d(ngf * 8, ngf * 4, 4, 2, 1, bias=False),
            nn.BatchNorm2d(ngf * 4),
            nn.ReLU(True),
            # state size. (ngf*4) x 8 x 8
            nn.ConvTranspose2d(ngf * 4, ngf * 2, 4, 2, 1, bias=False),
            nn.BatchNorm2d(ngf * 2),
            nn.ReLU(True),
            # state size. (ngf*2) x 16 x 16
            nn.ConvTranspose2d(ngf * 2,     ngf, 4, 2, 1, bias=False),
            nn.BatchNorm2d(ngf),
            nn.ReLU(True),
            # state size. (ngf) x 32 x 32
            nn.ConvTranspose2d(    ngf,      nc, 4, 2, 1, bias=False),
            nn.Tanh()
            # state size. (nc) x 64 x 64
        )

    def forward(self, input):
        output = self.main(input)
        return output

識別器

1. 負の領域の勾配も活用するために、nn.LeakyReLUを活性化関数として使用することが重要です。これらの勾配がなければ、生成器は更新できなくなってしまいます。
2. 識別器は、ネットワークの最後にnn.Sigmoid() を用いて入力を分類します。

class Discriminator(nn.Module):
    def __init__(self):
        super().__init__()
        self.main = nn.Sequential(
            # input is (nc) x 64 x 64
            nn.Conv2d(nc, ndf, 4, 2, 1, bias=False),
            nn.LeakyReLU(0.2, inplace=True),
            # state size. (ndf) x 32 x 32
            nn.Conv2d(ndf, ndf * 2, 4, 2, 1, bias=False),
            nn.BatchNorm2d(ndf * 2),
            nn.LeakyReLU(0.2, inplace=True),
            # state size. (ndf*2) x 16 x 16
            nn.Conv2d(ndf * 2, ndf * 4, 4, 2, 1, bias=False),
            nn.BatchNorm2d(ndf * 4),
            nn.LeakyReLU(0.2, inplace=True),
            # state size. (ndf*4) x 8 x 8
            nn.Conv2d(ndf * 4, ndf * 8, 4, 2, 1, bias=False),
            nn.BatchNorm2d(ndf * 8),
            nn.LeakyReLU(0.2, inplace=True),
            # state size. (ndf*8) x 4 x 4
            nn.Conv2d(ndf * 8, 1, 4, 1, 0, bias=False),
            nn.Sigmoid()
        )

    def forward(self, input):
        output = self.main(input)
        return output.view(-1, 1).squeeze(1)

これら2つのクラスは netG と netD として初期化されます。

GANの損失関数

ターゲットと出力の間のバイナリクロスエントロピーを使います。

criterion = nn.BCELoss()

設定

バッチサイズ opt.batchSize で長さが nz のランダムベクトルを用いて fixed_noise を設定します。また、実データ用のラベルと生成データ用のラベルをそれぞれ real_label と fake_label と呼びます。

fixed_noise = torch.randn(opt.batchSize, nz, 1, 1, device=device)
real_label = 1
fake_label = 0

そして、識別器と生成器のオプティマイザーを設定します。

optimizerD = optim.Adam(netD.parameters(), lr=opt.lr, betas=(opt.beta1, 0.999))
optimizerG = optim.Adam(netG.parameters(), lr=opt.lr, betas=(opt.beta1, 0.999))

訓練

学習の各エポックは2つのステップに分かれています。

ステップ1では、識別器ネットワークを更新します。これは2つの部分で行われます。まず、dataloaders から送られてくる本物のデータを識別器に与え、出力と real_label の間の損失を計算し、誤差逆伝播を用いて勾配を蓄積します。次に、fixed_noise を用いて生成器で生成されたデータを識別器に入力し、fake_label との間の損失を計算し、勾配を蓄積します。最後に、蓄積された勾配を用いて識別ネットワークのパラメータを更新します。

識別器を訓練している間に勾配が生成器に伝搬しないようにするために、偽データを計算グラフから切り離すことに注意してください。

また、最初に一度だけ zero_grad() を呼び出すだけで勾配のキャッシュがクリアされるので、実データと偽データの両方からの勾配が更新に利用できることにも注意してください。2回の .backward() コールはこれらの勾配を蓄積します。最後に、パラメータを更新するために optimizerD.step() を1回呼び出すだけです。

# train with real
netD.zero_grad()
real_cpu = data[0].to(device)
batch_size = real_cpu.size(0)
label = torch.full((batch_size,), real_label, device=device)

output = netD(real_cpu)
errD_real = criterion(output, label)
errD_real.backward()
D_x = output.mean().item()

# train with fake
noise = torch.randn(batch_size, nz, 1, 1, device=device)
fake = netG(noise)
label.fill_(fake_label)
output = netD(fake.detach())
errD_fake = criterion(output, label)
errD_fake.backward()
D_G_z1 = output.mean().item()
errD = errD_real + errD_fake
optimizerD.step()

ステップ2は生成ネットワークを更新することです。今回は、偽のデータを識別器に与えますが、real_labelで損失を計算します! ここでの目的は、本物のような$\vect{\hat{x}}$’sを作るように生成器を訓練することです。

netG.zero_grad()
label.fill_(real_label)  # fake labels are real for generator cost
output = netD(fake)
errG = criterion(output, label)
errG.backward()
D_G_z2 = output.mean().item()
optimizerG.step()