世界モデル(World Model)と敵対的生成ネットワーク(Generative Adversarial Network)

自律制御のための世界モデル

自己教師あり学習の最も重要な用途の一つは、制御のための世界モデル(World Model)を学習することです。人間がタスクを実行するとき、周りがどのように動くのかの内部モデルを心の中に持っています。例えば、9ヶ月目の赤ちゃんは物理学の直感を、ほとんど観察によって得ています。ある意味では、これは自己教師あり学習に似ています。何が起こるかを予測する学習によって、抽象的な原理が得られるのです。更に、内部モデルによって、私たちは世界に対して行動出来るようにもなりました。例えば、学習された物理学の直感と筋肉がどのように動くのかについての理解によって、落ちてくるペンをどうやって掴めるのかを予測し、そして掴むことができるのです。

「世界モデル」とは？

世界モデルとは、4つの大きいモジュールで構成される自律知能システムです（図1）。第一に、認識モジュールは世界を観測し、世界の状態の表現を計算します。この表現は完全ではありません。というのも、1) エージェントが全宇宙を観測してはおらず、2) 観測の精度が限られているためです。フィードフォワードモデルでは、認識モジュールは最初のタイムステップだけに存在することにも注意してください。第二に、Actorモジュール(方策モジュールとも呼ばれる)は、世界の表現に基づいて、何らかの行動をとることを想像します。第三に、モデルモジュールが、与えられた(時には潜在的な特徴を含んだ)世界の表現を基に、行動の結果を予測します。この予測は、次の世界の状態の推測として次のタイムステップに渡され、最初の時間ステップの認識モジュールと同じ役割を担います。図2は、このフィードフォワードの過程の詳細を示しています。最後に、criticモジュールがこの予測を、提案されたアクションを実行するためのコストに変換します。例えば、ペンが落ちている速度がこうで、筋肉をこう動かしたら、どれくらいペンを取り損ねるのか？などです。

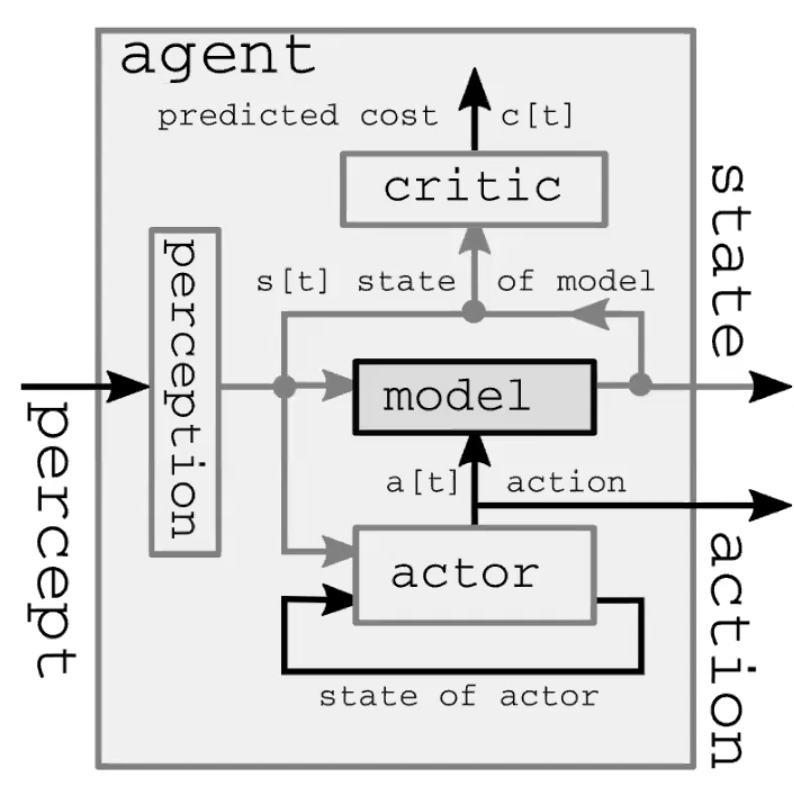
図1：自律知能システムの世界モデルの構造。

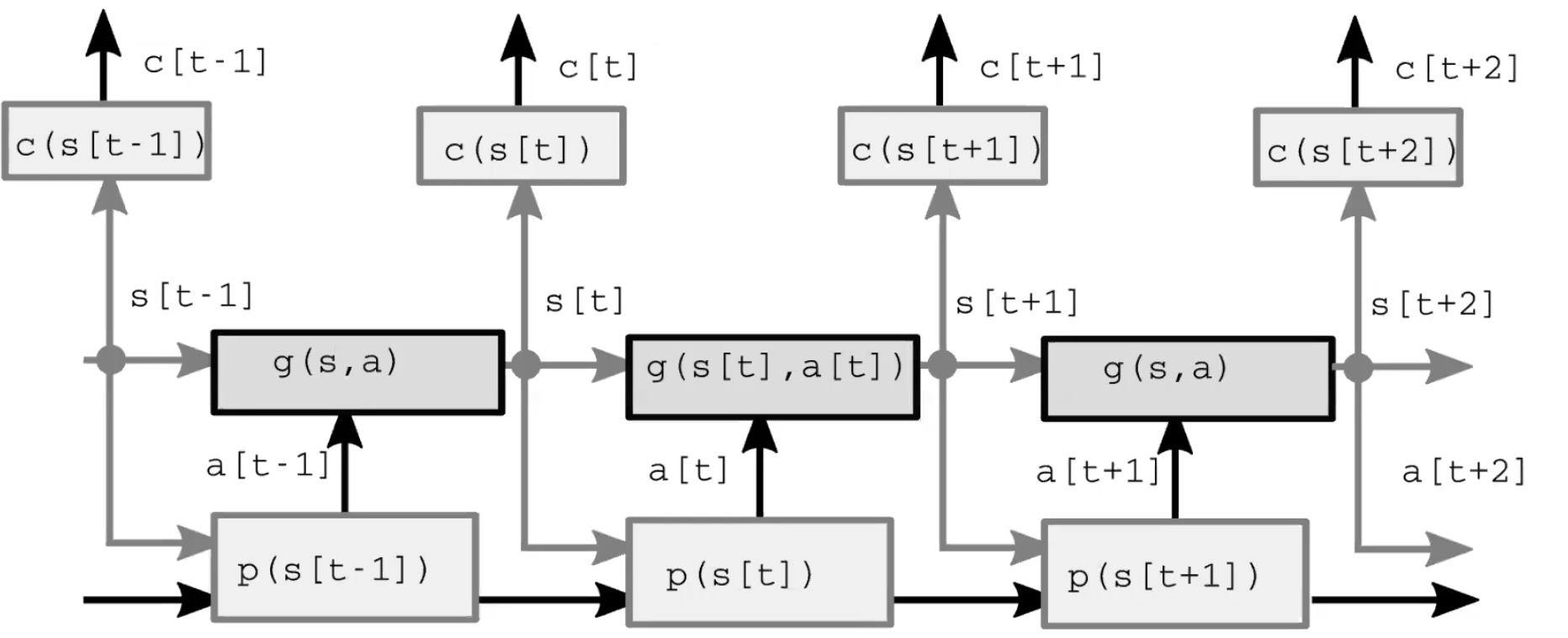
図2：モデルのアーキテクチャ。

古典的な設定

古典的な最適制御では、Actor(方策)モジュールのかわりに行動変数だけが存在します。この定式化はモデル予測制御と呼ばれる、古典的な方法で最適化されており、1960年代にNASAがロケットの軌道を計算するのに使われました。それはNASAが人間のコンピュータ（ほとんどが黒人女性の数学者）から電子コンピュータへの切り替えを行った時でした。このシステムのイメージとしては、非展開RNN、潜在変数としての行動、そして誤差逆伝播と勾配法(離散的行動に動的計画法など他の手法も可能)で、タイムステップごとのコストの合計を最小化する行動系列を推論していると考えられます。

ちなみに、ここで潜在変数を「推論」し、パラメータを「学習」するという言葉遣いになっていますが、これらを最適化する過程は大体似ています。一つ重要な違いは、潜在変数がサンプル毎に値をとるのに対し、パラメータはサンプル間で共有されているということである。

ある改良

行動を計画する毎に複雑な誤差逆伝播を行うのは避けたいので、変分オートエンコーダのスパースコーディングを改善するために使ったのと同じトリックを使います。つまり、世界の表現から直接、最適な行動系列を予測する符号化器を学習します。このために使われる符号化器は、方策ネットワークと呼ばれます。

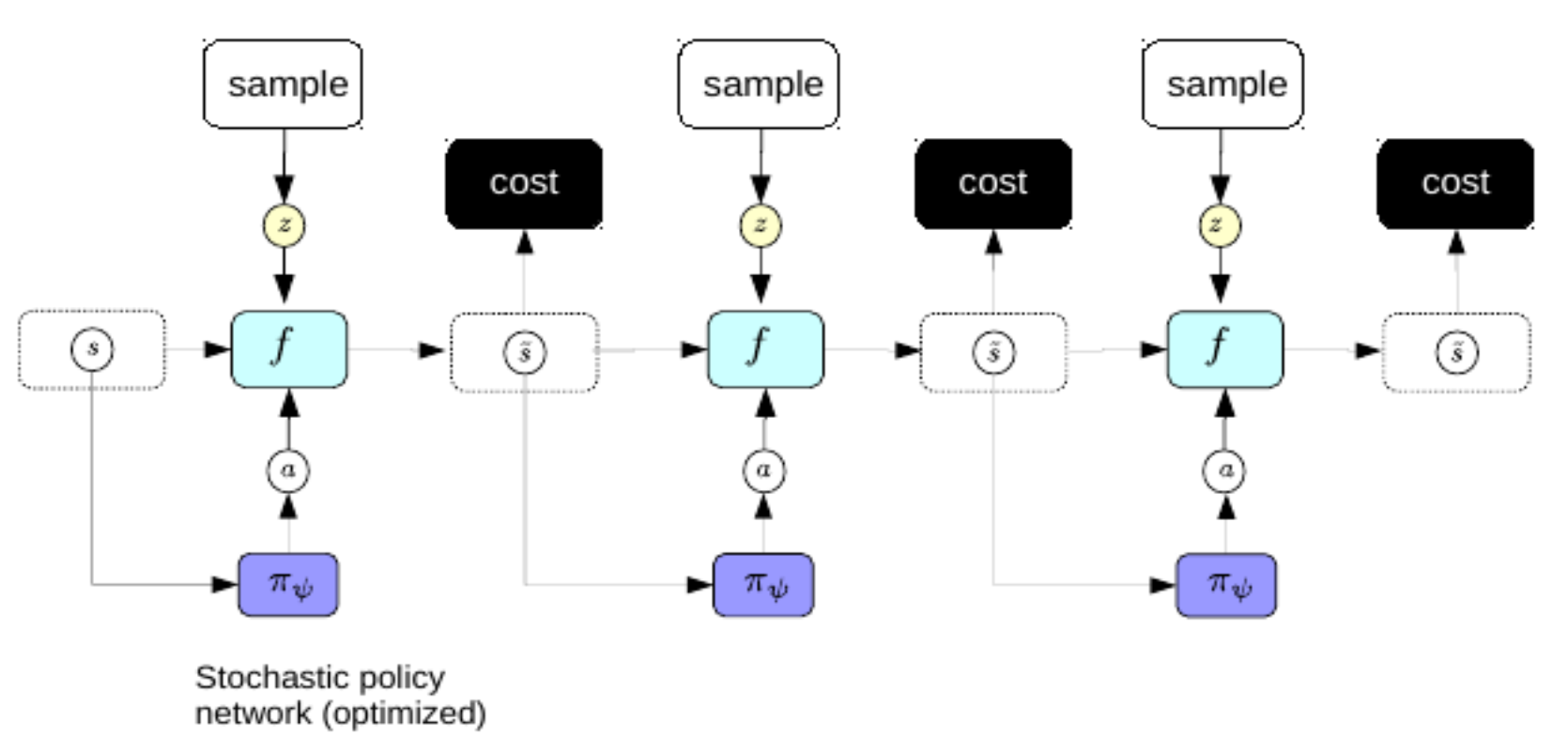
図3: 方策ネットワーク。

学習済みの方策ネットワークを使って、認識した直後に最善の行動系列を予測することができます。

強化学習 (RL)

RLとこれまで学んてきたものとの主な違いは2つあります。

1. 強化学習の環境のコスト関数はブラックボックスです。言い換えれば、エージェントは報酬の仕組みを理解していません。
2. RLの設定では、環境を進めるために世界のモデルを使うのではなく、実世界に行動して、何が起こるかを観測することで学習します。実世界では、完璧に状態を観測することができないため、次の出来事を予測できない場合もあり得ます。

強化学習の主の問題は、コスト関数が微分できないことです。結果的に、試行錯誤によって学習するしかなくなります。そうなると、いかに効率的に状態空間を探索するかが問題になります。これを解決したら次の課題は、探索と利用という基本的な問題です。つまり、環境について最大限に学ぶために行動をとるか、学んだ知識を利用して報酬が最大化出来る行動を優先するかの二択です。

ActorとCriticを両方学習させる、人気のあるActor-Critic系強化学習のアルゴリズムというものがあります。強化学習の手法はだいたい同じく、コスト関数のモデル(critic)を学習させています。Actor-Critic系でのcriticの役割は、価値関数の期待値を学習することです。Criticがニューラルネットだったので、モジュールを通じた勾配逆伝播が可能になります。Actor(「役者」)が環境の中で取るべき行動を提案し、Critic(「批評家」)がコスト関数のモデルを学習します。ActorとCriticの連携で、Criticを使わないよりもっと効率的な学習が可能になります。世界の良いモデルを持っていなければ、学習するのは難しくなります。例えば、崖の隣の車は、崖から落ちることを知らないととてもまずいことになるでしょう。人間や動物はとても良い世界モデルを頭の中に持っているため、RLのエージェントより遥かに早く学習することができます。

「偶然的不確定性」と「認識論的不確定性」といった不確定性のせいで、そもそも未来を予測できない場合もあります。偶然的不確定性の原因は、環境の中の制御・観測不可能な要素が存在することです。そして認識論的不確定性は、モデルに学習データがまだ足りないから、未来を予測できないことを指します。

世界モデルは以下のものを予測します。

ここで$z$は値がわからない潜在変数です。$z$で表すのは、わからないけど予測に影響を与える要素(すなわち偶然的不確定性)です。$z$を正則化するために、スパース性、ノイズ、または符号化器を使うことができます。世界モデルでプランニングを学習できます。このシステムは、復号化器に状態の表現と不確定性$z$を復号化させることで動きます。$\hat s_{t+1}$と実際に観測された$s_{t+1}$の差を最小化するような$z$が最も良い$z$として定義されます。

敵対的生成ネットワーク

敵対的生成ネットワーク(Generative Adversarial Network、GAN)には多くのバリエーションがありますが、ここでは対照法を用いたエネルギーベースモデルの一種として考えます。GANは訓練用のサンプルのエネルギーを押し下げると同時に、対照サンプルのエネルギーを押し上げます。基本的なGANは2つの部分から構成され、対照サンプルを知的に生成する生成器と、識別器（Criticとも）というコスト関数として使われるエネルギーモデルをもちます。生成器と識別器は両方ともニューラルネットです。

GANへ訓練と対照の2種類のサンプルが入力されます。訓練サンプルは識別器に通され、そのエネルギーを下げます。対照サンプルは、何らかの分布から潜在変数をサンプリングし、それをジェネレーターに通して、訓練標本に似たものを生成させ、識別器に通し、そのエネルギーを上げます。識別器のロス関数は次のようなものです。

ここでの$L_d$は、$F(y)$を減らしつつ$F(\bar{y})$を増やせられるものであれば、マージンベースの損失関数(例えば、$F(y) + [m - F(\bar{y})]^+$ or $\log(1 + \exp[F(y)]) + \log(1 + \exp[-F(\bar{y})])$)でも問題はありません。ここの$y$がラベルで、$\bar{y}$は、$y$自身を除いて最もエネルギーを低くする変数です。

生成器のロス関数は少し違います。

ここで$z$は潜在変数で、$G$が生成器のニューラルネットです。生成器は、識別器を騙せるようなエネルギーが低い$\bar{y}$を生成するように重みを調整します。

このタイプのモデルが敵対的生成ネットワークと呼ばれる理由は、2つのお互いに敵対している目的関数持ち、それらを同時に最小化していることである。これらの2つの関数間のナッシュ均衡を見つけようとしていますが、勾配降下法はデフォルトではこれができないので、この問題は勾配降下法で扱える問題ではありません。

真の多様体に近いサンプルを持っている場合は問題があります。無限に薄い多様体があるとします。すると識別器は、多様体の外側では $0$ の確率を、多様体上では無限大の確率を出力する必要があります。これは非常に難しいので、GANはシグモイドを使って、多様体の外側では$0$を出力し、多様体上では$1$を出力させます。しかし、識別器を多様体の外側で$0$を生成するように学習させてしまえば、そのエネルギー関数が全く使えなくなってしまいます。エネルギー関数が滑らさを失い、多様体の外側のエネルギーがすべて無限大になり、内側のエネルギーが$0$になってしまうからです。エネルギー値が小さなステップで $0$ からすぐ無限大になることは望ましくありません。これを解決するため、エネルギー関数を正規化する手法が多く提案されています。改良されたGANの良い例として、識別器の重みの大きさを制限するWasserstein GANがあります。