Discriminative Recurrent Sparse Auto-Encoder and Group Sparsity

識別リカレントスパースオートエンコーダー (DrSAE)

DrSAEのアイデアは、スパース符号化（スパースオートエンコーダー）と識別タスクの訓練を組み合わせることです。

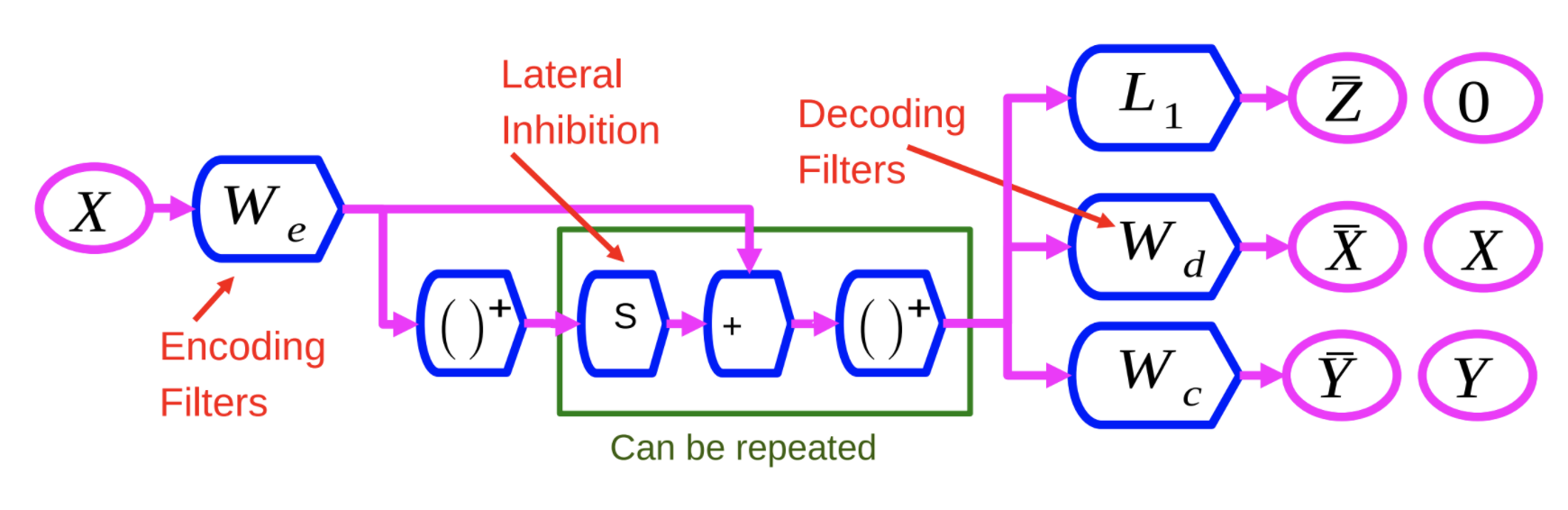
図1: 識別リカレントスパースオートエンコーダー

エンコーダである $W_e$ は、LISTA 法のエンコーダに似ています。変数$X$は、$W_e$ によって線形変換されたあと、非線形変換を施されます。この結果に別の学習済み行列 $S$ を掛け合わせて $W_e$ に加算します。その後、別の非線形変換が適用されます。このプロセスはその一つ一つを層として、何度も繰り返すことができます。

このニューラルネットワークを3つの指標に基づいて訓練します。

1. $L_1$: $L_1$ノルムを用いることで、特徴ベクトル$Z$をスパースにします。
2. $X$の再構成: 入力から出力を再現するデコーディング行列を用いることで、$X$の再構成を行います。これは、図1の$W_d$で示されている二乗誤差を最小化することで行われます。
3. 第3項を追加します。$W_c$で示されるこの第3項は、カテゴリを予測しようとする単純な線形分類器です。

これらの3つの指標のすべてを同時に最小化するように訓練を行います。

これらの指標を考える利点は、入力を再構成できる表現を見つけるように強制することで、基本的には入力に関する情報をできるだけ多く含む特徴を抽出するようなバイアスを持たせられることです。言い換えれば、これらの指標を考えることで、豊かな特徴を書くとすることができるということです。

グループスパース性

ここでのアイデアは、畳み込みで抽出された通常の特徴ではなく、基本的にはプールした後にスパースとなる特徴を作り出すことで、スパースな特徴を生成するというものです。

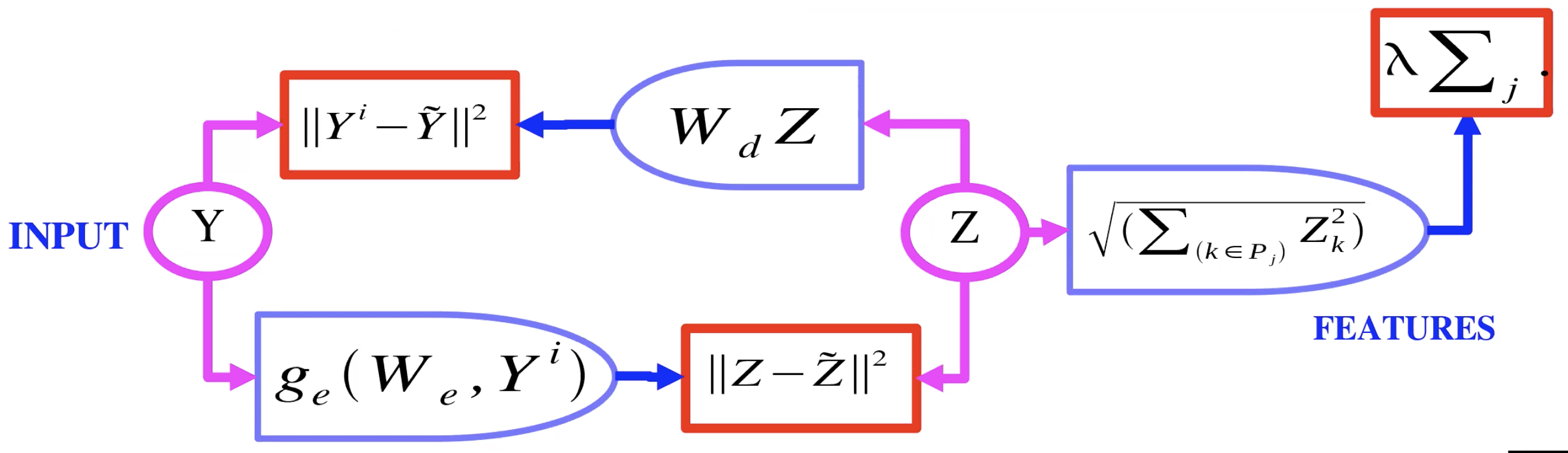
図2: グループスパース性のあるオートエンコーダ

図2は、グループスパース性を持つオートエンコーダーの例を示しています。ここでは、潜在変数$Z$の$L_1$ノルムを計算するのではなく、基本的にはグループ上の$L_2$ノルムを計算します。つまり、$Z$のグループの各成分の $L_2$ ノルムを取り、それらの和を取ります。これが正則化として使用されるので、$Z$のグループをスパースにすることができます。これらのグループ（特徴表現のプール）は、互いに似た特徴をグループ化する傾向があります。

グループスパース性のあるオートエンコーダーについての質問と説明

Q: 最初のスライドで使用されているような分類器と正則化を用いた方法と類似の方法は、VAEに適用できますか？

A: VAEにおいて、ノイズを付加することと、スパース性を強制することはå、潜在変数/コードが持つ情報を減らす2つの方法となっています。これによって恒等写像を学習してしますことを防ぐことができます。

Q:「グループスパース性を用いたオートエンコーダー」というスライドにある、$P_j$とは何ですか？

A: $P$は特徴表現のプールです。ベクトル $z$ に対しては、これは $z$ の値の部分集合になります。

Q: 特徴プールについての説明。

A: (Yann はグループスパース性を持つオートエンコーダーの表現を描く) エンコーダは、プールされた特徴の $L_2$ ノルムを用いて正則化された潜在変数 $z$ を生成します。この $z$ は、デコーダによって画像の再構成に利用されます。

Q: グループ正則化は、類似した特徴をグループ化するのに役立ちますか？

A: 不明です。ここで行われた作業は、計算能力がまだ低く、データが容易に入手できなかった時に行われていたものです。今は役立つかどうかはわかりません。

画像レベルの学習、局所フィルタはあるが重み共有はない場合

役に立つかどうかについての答えは明確ではありません。これに興味がある人は、画像復元に興味があるか、ある種の自己学習に興味があるかのどちらかです。これは、データセットが非常に小さい場合にうまくいくでしょう。畳み込みエンコーダとデコーダを、その複雑型細胞上でグループスパース性を使って学習した場合、事前学習が終わった後に、デコーダを取り除き、エンコーダだけを特徴抽出器として使用します。

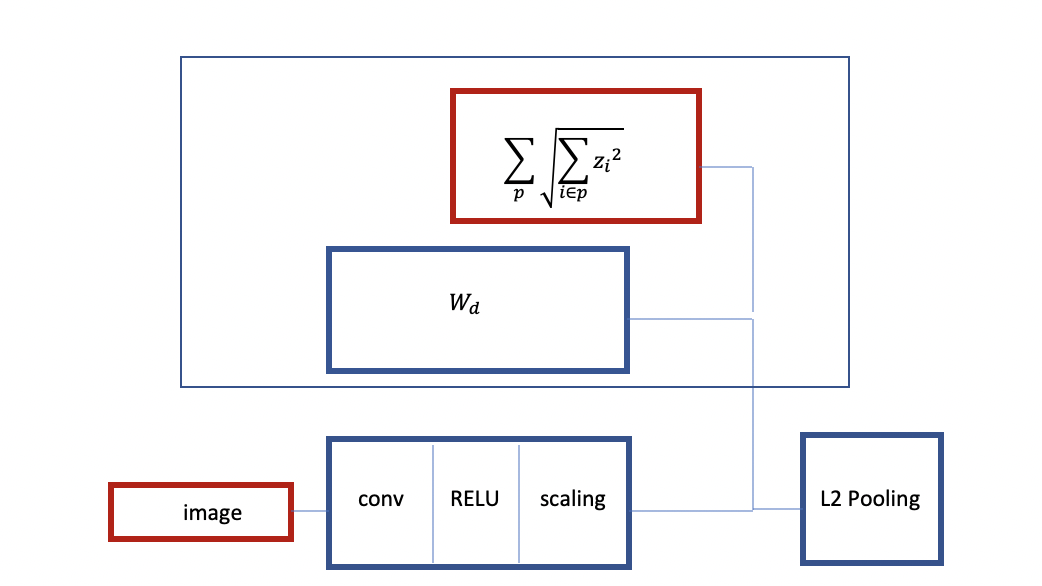
図3：グループスパース性のある畳み込みReLUネットの構造

上で見たように、画像を入力として、基本的には畳み込みReLUネットであるエンコーダがあり、ある種のスケーリング層がその後に続きます。グループスパース性を用いて学習するとします。線形デコーダと1、としてグループされている指標を用いて、グループスパース性によって正則化を行います。これは、グループスパース性に似たアーキテクチャを持つ L2 プーリングのようなものです。

このネットワークの別のインスタンスを学習することもできます。今回は、より多くの層を追加して、L2プーリングとスパース性を測る指標を持つデコーダの出力層のプーリングによって、入力を再構成するように訓練します。これにより、事前に訓練された2層の畳み込みネットが作成されます。これはスタックドオートエンコーダーとも呼ばれます。ここでの主な特徴は、グループスパース性を持つ不変な特徴を生成するように訓練されることです。

Q : ありうるすべての部分木をグループとして使うべきですか？

A : それはあなた次第です。必要以上に大きな木で訓練して、滅多に使わない枝を削除することもできます。

図4: 画像レベルの学習、局所フィルタはあるが重み共有はない

これらはピンホイールパターンと呼ばれています。これは特徴量の整理の仕方の一種です。赤い点の周りを回ると、様々な向きに連続的に変化していきます。私たちがそれらの赤い点の一つを取って、赤い点の周りに少し円を描くと、移動するにつれて抽出器の向きが連続的に変化することに気づくでしょう。脳でも同じような傾向が見られます。

Q : グループスパース性の項は小さな値となるように訓練されるのですか？

グループスパース性の項は正則化項です。ですので項自体は訓練されておらず、固定されています。それは単にグループのL2ノルムなので、グループはあらかじめ決まっていることになります。しかし、それはスパース性の基準ですので、エンコーダとデコーダが何をするか、どのような種類の特徴を抽出するかがこれによって決まります。

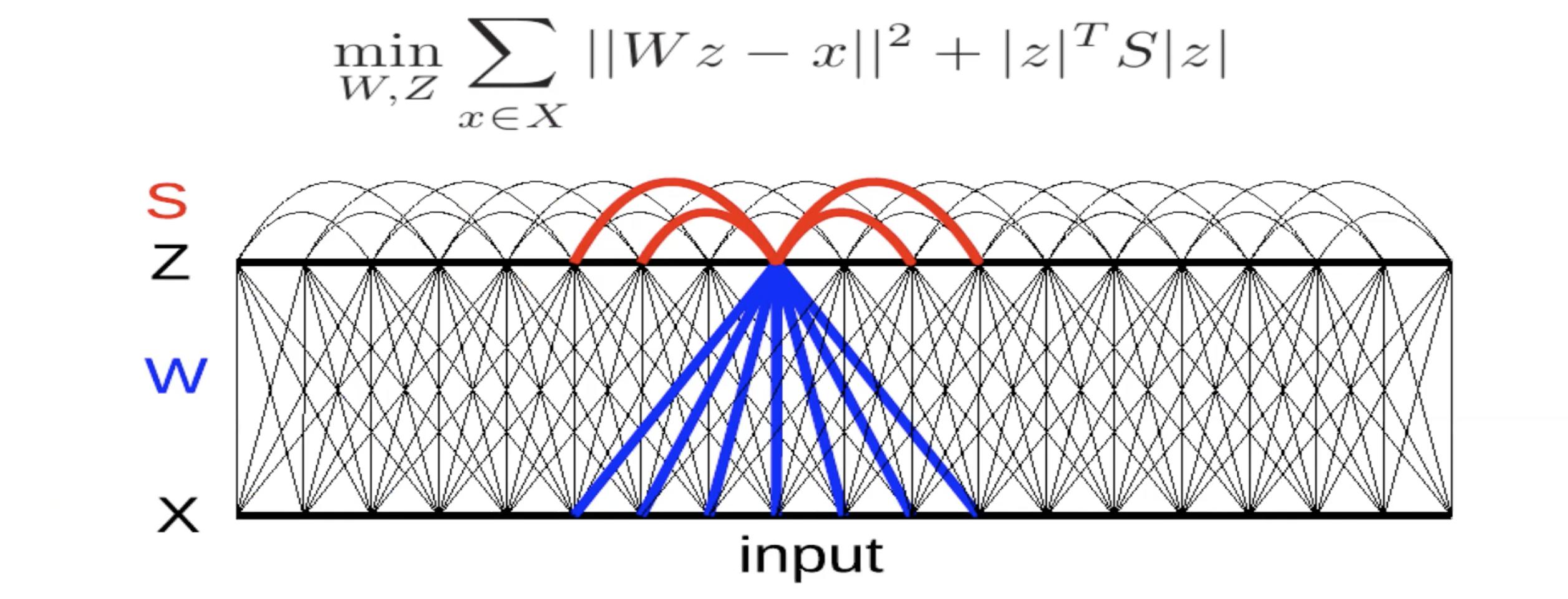
図5: 側方抑制による不変な特徴

ここで、二乗再構成誤差を持つ線形デコーダを考えます。エネルギーにはスパース性の指標となる項があります。行列$S$は、手動で決定されるか、この項が最大になるように学習されます。$S$の項が正で大きい場合は、 $z_i$ と $z_j$ を同時にオンにしたくないということを意味します。したがって、これは一種の相互抑制です（神経科学では自然抑制と呼ばれています）。したがって、できるだけ大きな$S$の値を見つけようということになります。

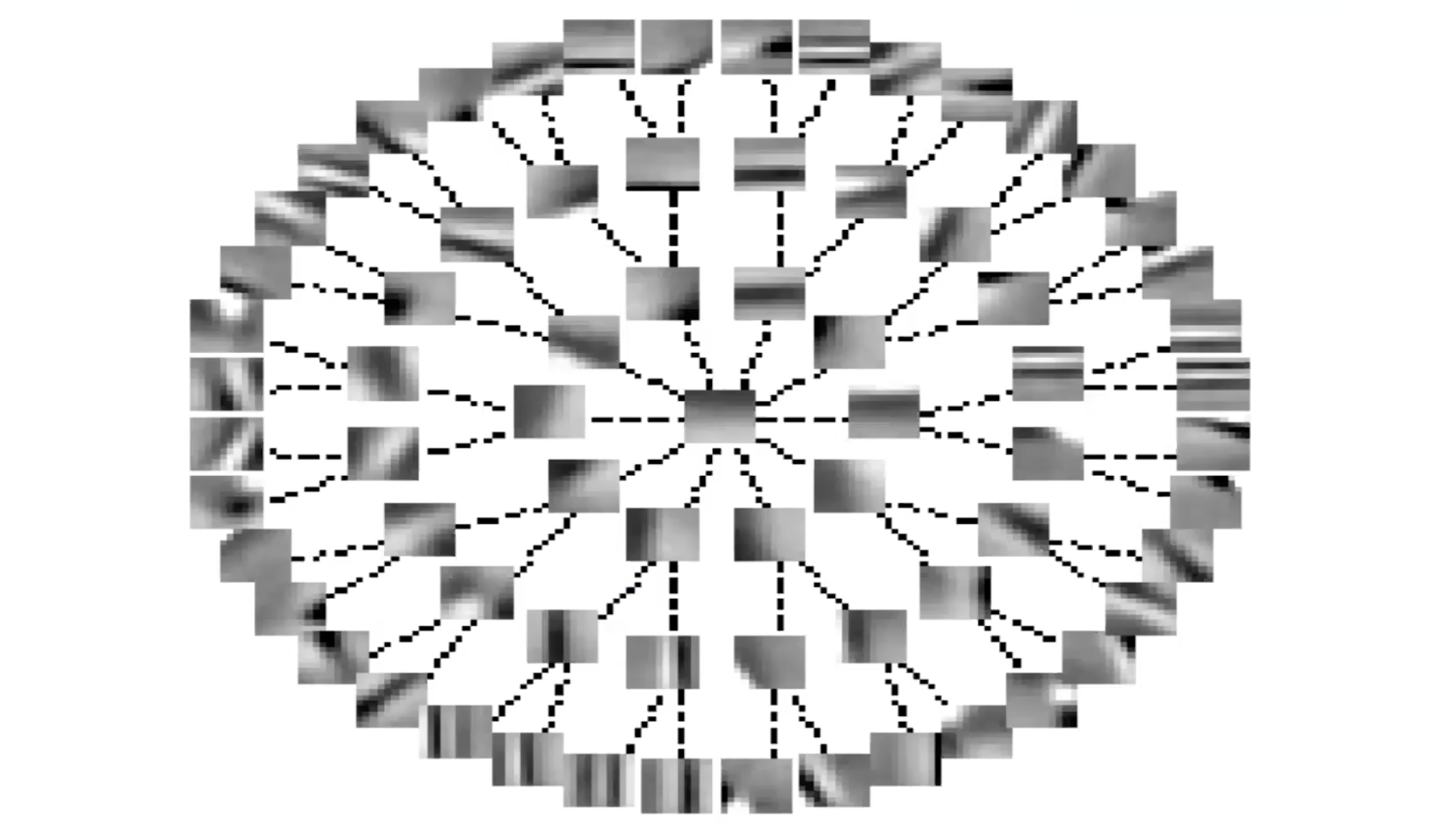
図6: 側方抑制による不変な特徴 (木構造)

$S$を木として整理すると、線は$S$行列のゼロである項を表します。線がないときはいつでも、ゼロではない項があります。つまり、すべての特徴は、木の上にあるものや木の下にあるものを除いて、他のすべての特徴を阻害しているということになります。これは、グループスパース性の逆のようなものです。

システムは多かれ少なかれ連続的に特徴を整理していることがわかります。木の枝に沿った特徴は、選択性のレベルが異なる同じ特徴を表しています。抑制がないので、周辺部に沿った特徴は多かれ少なかれ連続的に変化します。

各イテレーションで $x$ を与え、このエネルギー関数を最小化する $z$ を見つけることでこのシステムを訓練します。勾配降下法を１ステップ行って $W$ を更新し、 $S$ の項を大きくすることもできます。