Generative Models - Variational Autoencoders

復習: オートエンコーダー (AE)

大まかに要約すると、非常にシンプルなオートエンコーダー(AE) は次のとおりです。

• 最初に、オートエンコーダーは入力を受け取り、アフィン変換を介して隠れ状態に写像します$\boldsymbol{h} = f(\boldsymbol{W}_h \boldsymbol{x} + \boldsymbol{b}_h)$。ここで、$f$は（要素ごとの）活性化関数です。 これは エンコーダー のステージです。$\boldsymbol{h}$は　コード　とも呼ばれます。
• 次に、$\hat{\boldsymbol{x}} = g（\boldsymbol {W} _x \boldsymbol {h} + \boldsymbol {b} _x）$です。ここで$g$は活性化関数です。 これはデコーダーステージです。

詳細な説明については、第7週のメモを参照してください。

VAEの背後にある直感と従来のオートエンコーダーとの比較

次に、生成モデルの一種である変分オートエンコーダー（またはVAE）を紹介します。なぜ生成モデルまで気にするのかというと、識別モデルはいくつかの観察を与えられて結果を予測することについて学習しますが、生成モデルはデータ生成プロセスをシミュレーションすることを目的としているからです。 よって、生成モデルは背後の因果関係をよりよく理解することができ、そのおかげでよりよく汎化することができます。

VAEの名前には「オートエンコーダー」（AE）が含まれていますが（オートエンコーダーと構造的またはアーキテクチャ的に類似しているため）、定式化の上では大きく異なります。以下の図1を参照してください。

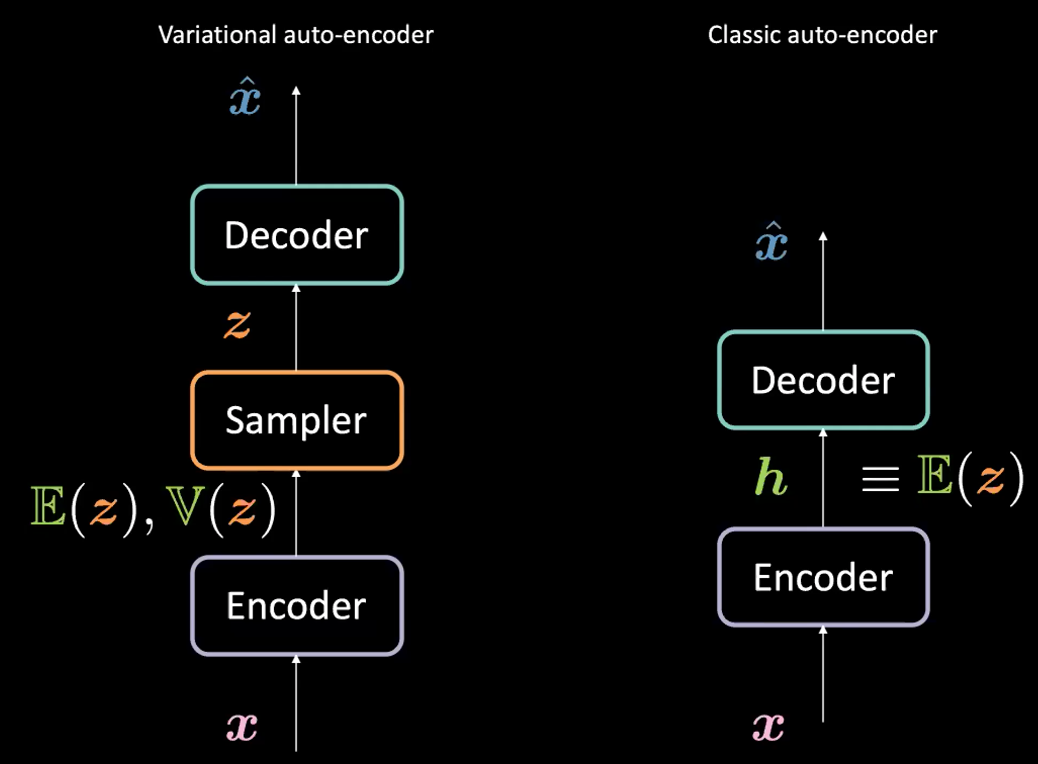
図1: VAE *vs.* 通常の AE

変分オートエンコーダー（VAE）と通常のオートエンコーダー（AE）の違いは何ですか？

VAEの場合：

• 最初に、エンコーダーステージについてです：入力$\boldsymbol{x}$をエンコーダーに渡します。 AEで隠れ表現$\boldsymbol{h}$（コード）を生成する代わりに、VAEのコードは$\mathbb{E}(\boldsymbol{z})$と$\mathbb{V}(\boldsymbol{z})$の２種類があります。ここで、$\boldsymbol{z}$は、平均$\mathbb{E}(\boldsymbol{z})$と分散$\mathbb{V}(\boldsymbol{z})$を持つガウス分布に従う潜在確率変数です。実際には、エンコードされた分布としてはガウス分布ではない分布も使用できます。
• エンコーダーは$\mathcal{X}$から$\mathbb{R}^{2d}$への関数$\boldsymbol{x} \mapsto \boldsymbol{h}$です。ただし、ここでは$\boldsymbol{h}$で、$\mathbb {E}(\boldsymbol {z})$と$\mathbb{V}(\boldsymbol {z})$の連結を表しています。
• 次に、エンコーダーによってパラメトライズされた上記の分布から$\boldsymbol{z}$をサンプリングします。具体的には、$\mathbb{E}(\boldsymbol{z})$と$\mathbb{V}(\boldsymbol {z})$がサンプラーに渡され、潜在変数$\boldsymbol{z}$が生成されます。
• 次に、$\boldsymbol{z}$がデコーダーに渡され、$\hat{\boldsymbol{x}}$が生成されます。
  • デコーダーは$\mathcal{Z}$から$\mathbb{R}^{n}$への関数$\boldsymbol{z} \mapsto \boldsymbol{\hat{x}}$です。

実際、通常のオートエンコーダの場合、$\boldsymbol{h}$はVAEの定式化におけるベクトル$\E(\boldsymbol{z})$とみなすことができます。要するに、VAEとAEの主な違いは、VAEは生成プロセスを可能にする優れた潜在空間を有しているということです。

VAEの目的（損失）関数

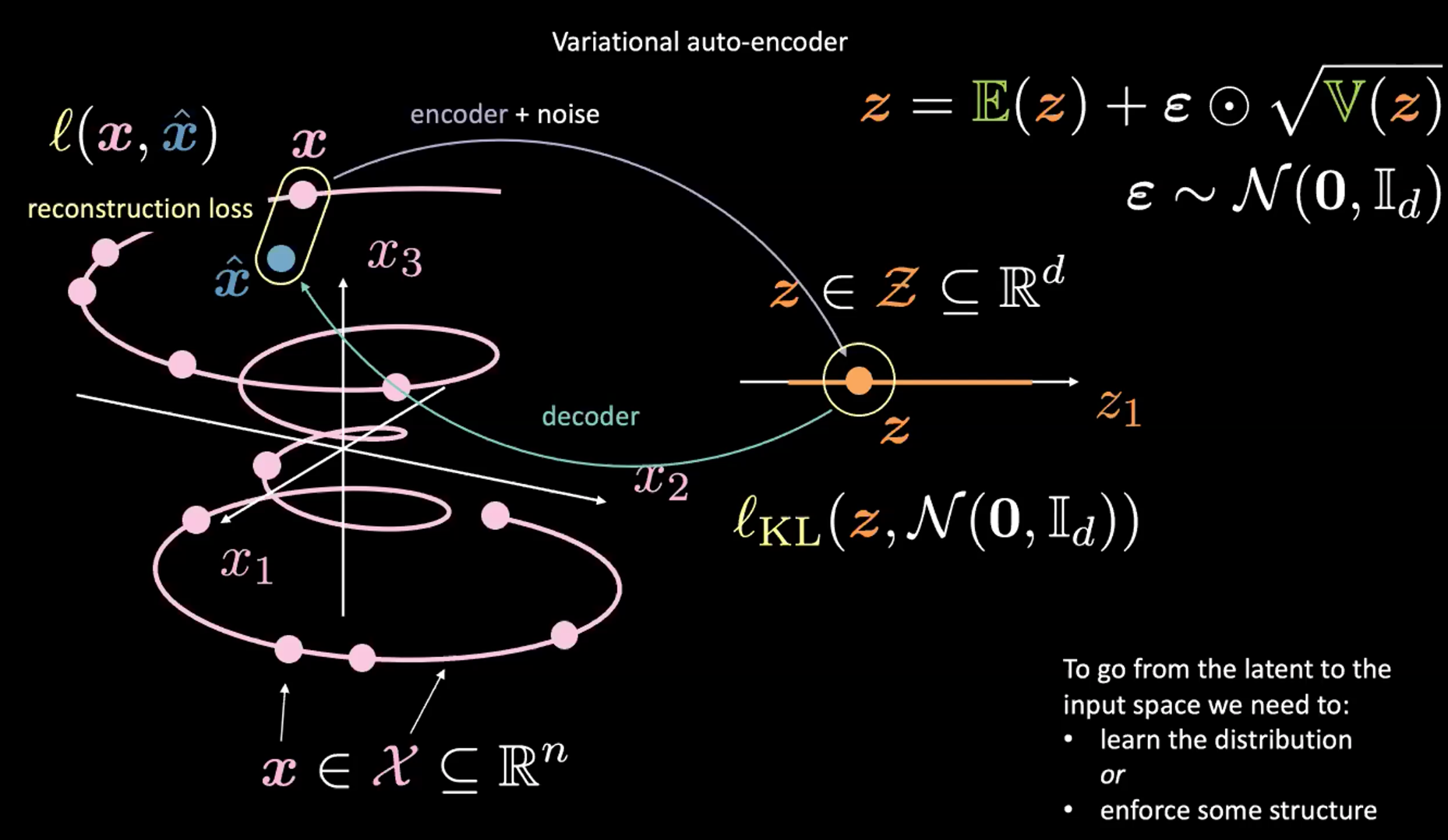
図2: 入力空間から潜在空間への写像

上記の図2を参照してください。とりあえずは右上のもの（次のセクションで説明するreparametrization trick）は無視してください。

まず、エンコーダーとノイズを使用して、入力空間（左）から潜在空間（右）にエンコードします。次に、潜在空間（右）から出力空間（左）にデコードします。潜在空間から入力空間（生成プロセス）に移行するには、（潜在コードの）分布を学習するか、何らかの構造を強制する必要があります。今回の場合、VAEは潜在空間に何らかの構造を強制するようにします。

いつものように、VAEを訓練するために、損失関数を最小化します。損失関数は、再構成項と正則化項で構成されます。

• 再構成項は最終層（図の左側）にあります。これは、図の$l(\boldsymbol{x}, \hat{\boldsymbol{x}})$に対応します。
• 正則化項は潜在層にあり、潜在空間（図の右側）に特定のガウス構造を適用します。これを行うには、ペナルティ項$l_{KL}(\boldsymbol{z}, \mathcal{N}(\boldsymbol{0}, \boldsymbol{I}_d))$を使用します。これがないと、VAEは普通のオートエンコーダーのように機能し、オーバーフィッティングしてしまう可能性があり、私たちが必要としている、生成する能力を得ることができません。

サンプリング$\boldsymbol{z}$に関する議論（reparametrization trick）

VAEのエンコーダーによって返される分布からどうやってサンプリングをするのでしょうか？ 上記によると、$\boldsymbol{z}$は、ガウス分布からサンプリングします。 ただし、VAEモデルを訓練するために勾配降下法をも用いる場合、サンプリング・モジュールを介して逆伝播を実行する方法がわからないため、これは問題になります。

代わりに、reparametrization trickを使用して$\boldsymbol{z}$を「サンプリング」します。$\boldsymbol{z} = \mathbb{E}(\boldsymbol{z}) + \boldsymbol{\epsilon} \odot \sqrt{\mathbb{V}(\boldsymbol{z})}$を使用します。ここで$\epsilon\sim \mathcal{N}(\boldsymbol{0}, \boldsymbol{I}_d)$です。この場合、訓練時に逆伝播をすることが可能です。 具体的には、勾配は上記の式の（要素ごとの）積と和を通過します。

VAEの損失関数の分析

潜在変数の推定値と再構成損失の可視化

上記のように、VAEの損失関数には、再構成項と正則化項の2つの部分が含まれます。 これは次のように書くことができます

損失関数の各項を可視化するために、推定された各$\boldsymbol{z}$の値を、円の中心が$\mathbb{E}(\boldsymbol{z})$で、その周辺の領域が$\mathbb{V}(\boldsymbol{z})$によって定まる$\boldsymbol{z}$のとりうる値であるような、$2$次元空間の円と考えることができます。

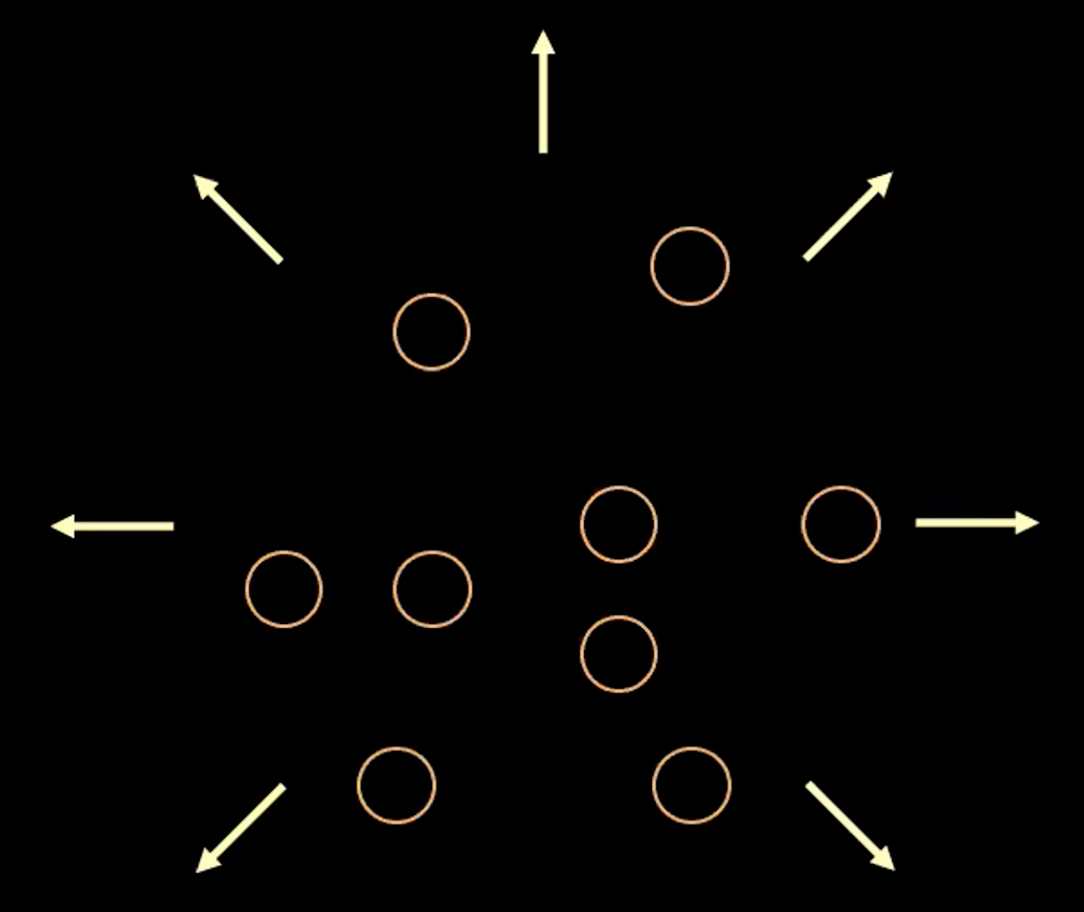
図3: 潜在空間における円としてのベクトル$z$の可視化

上記の図3では、各円は$\boldsymbol{z}$の推定領域を表し、矢印は再構成項が各推定値を他の推定値から遠ざける方法を表しています。これについては以下で詳しく説明します。

$z$の任意の2つの推定値の間に重なりがある場合（視覚的には、2つの円が重なっている場合）、重なっている領域の中の点を両方の元の入力にマッピングできるため、再構成にあいまいさが生じます。 したがって、再構成損失は、点を互いに遠ざけます。

ただし、再構成損失のみを使用すると、推定値は互いに離れたままになり、システムが発散する可能性があります。これがペナルティ項を考える理由です。

注：バイナリ入力の場合、再構成損失は

実数値の入力の場合、再構成損失は

ペナルティ項

2番目の項は、平均$\mathbb{E}(\boldsymbol {z})$、分散$\mathbb{V}(\boldsymbol{z})$のガウス分布に由来する$\boldsymbol{z}$と標準正規分布の間の相対エントロピー（2つの分布の間の距離）です。 この第2項をVAE損失関数で拡張すると、次のようになります。

各式には合計すると4つの項があります。 以下に、図4の最初の3つの項を書き出してグラフ化します。

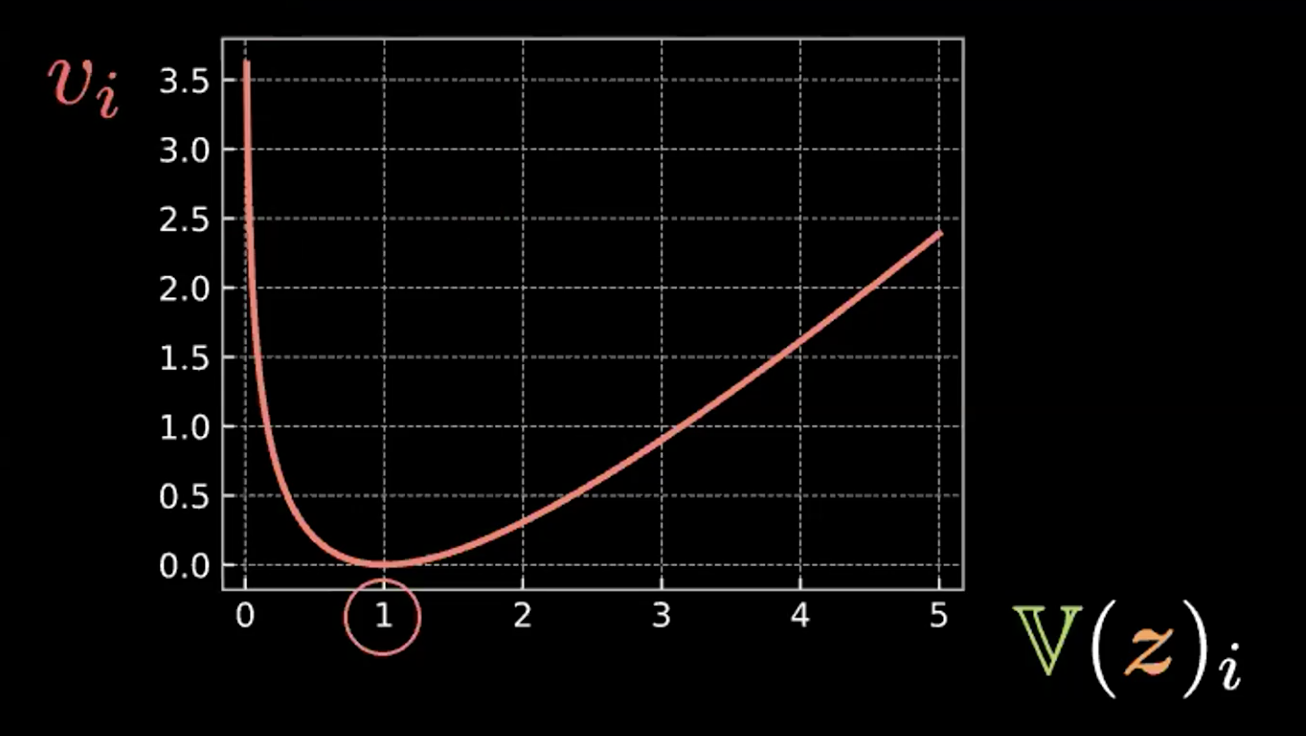
図4: 相対エントロピーがどのようにして円の分散が1となるように強制するかを示したプロット

この計算をみると、$z_i$の分散が1の場合、この式が最小化されることがわかります。したがって、ペナルティ損失により、推定された潜在変数の分散が約1に保たれます。視覚的には、上の「バブル（円）」の半径は約1になります。

最後の項$\mathbb{E}(z_i)^2$は、$z_i$間の距離を最小化するため、再構成項によって促進される発散を防ぎます。

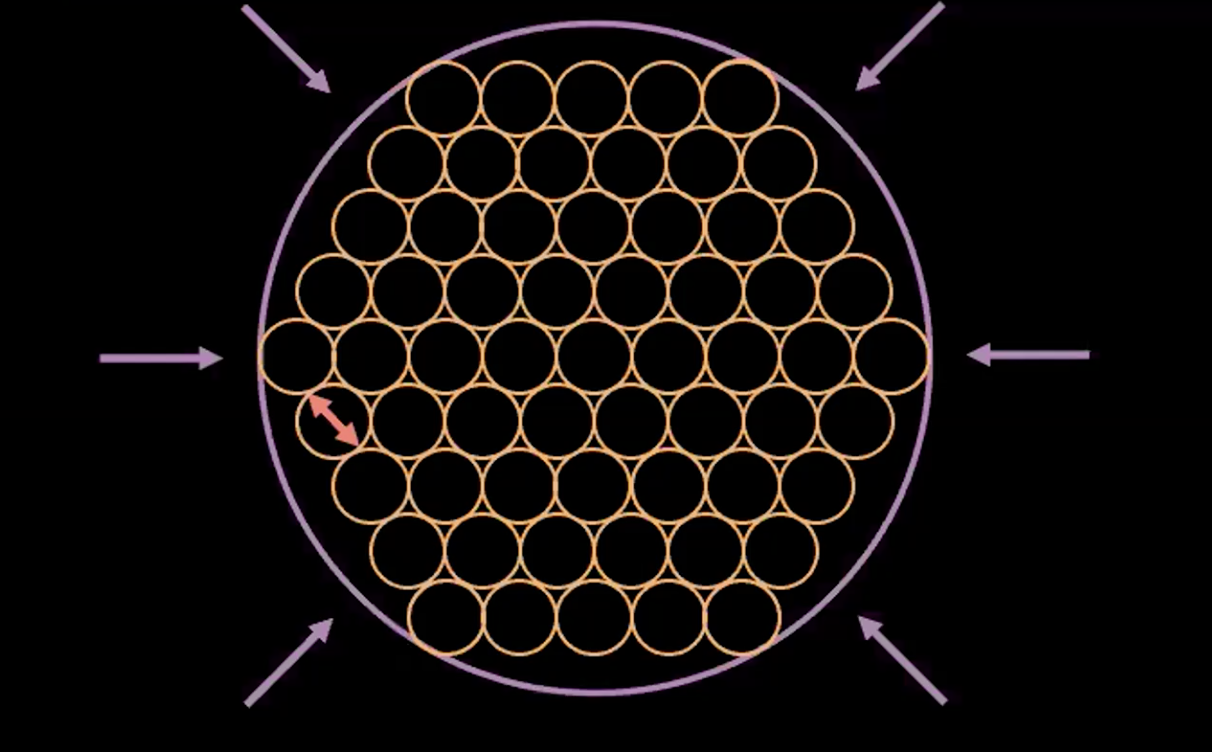
図5: 「バブルのバブル」としてのんVAEの解釈

上の図5は、VAE損失が、どのようにして各点の推定分散を1前後に保ちながら、推定された潜在変数を重なり合わせずにできる限り近づけたかを示しています。

注： VAE損失関数の$\beta$は、再構成項とペナルティの項を重みでバランスするハイパーパラメーターです。

Variational Autoencoder（VAE）の実装

このノートブックでは、VAEを実装し、MNISTデータセットで訓練します。 次に、正規分布から$\boldsymbol{z}$をサンプリングしてデコーダーにフィードし、結果を比較します。 最後に、2次元射影で$\boldsymbol{z}$がどのように変化するかを見ていきます。

注：使用されているMNISTデータセットでは、ピクセル値は$[0、1]$の範囲で正規化されています。

エンコーダーとデコーダー

1. 「VAE」モジュールでエンコーダーとデコーダーを定義します。
2. エンコーダーの最後の線形層について、出力をサイズを$2d$とします。前半の$d$は平均であり、後半の$d$は分散です。前のreparameterisation trickで説明したように、これらの平均と分散を使用して$\boldsymbol{z} \in R^d$をサンプリングします。
3. デコーダーの最後の線形レイヤーでは、入力データと同様に、範囲$[0、1]$で出力できるように、シグモイド活性層を使用します。

class VAE(nn.Module):
    def __init__(self):
        super().__init__()

        self.encoder = nn.Sequential(
            nn.Linear(784, d ** 2),
            nn.ReLU(),
            nn.Linear(d ** 2, d * 2)
        )

        self.decoder = nn.Sequential(
            nn.Linear(d, d ** 2),
            nn.ReLU(),
            nn.Linear(d ** 2, 784),
            nn.Sigmoid(),
        )

###　Reparameterisationと forward関数

reparameterise関数については、モデルを訓練するとき、対数分散（ logvar）から標準偏差（ std）を計算します。分散が負ではないことを保証するために対数分散を使用します。その対数を取ると、分散の全範囲が確保され、訓練がより安定します。

訓練中、reparameterise関数がreparametrization trickを実行するため、逆伝播を実行することができます。講義で説明したように、上記に書いて黄色いバブルの概念に接続するために、この関数が呼び出されるたびに、eps = std.data.new(std.size()).normal_()で点を描画します。 正規分布であるため、100回実行すると100個の点で結成された大きい球が得られ、この線 eps.mul（std）.add_（mu）により、球は muを中心とし、半径はstdになります。

forwardでは、最初にエンコーダーからmu（前半）と logvar（後半）を計算し、次にreparameterise関数を介して$\boldsymbol{z}$を計算します。最後に、デコーダーの出力を返します。

def reparameterise(self, mu, logvar):
    if self.training:
        std = logvar.mul(0.5).exp_()
        eps = std.data.new(std.size()).normal_()
        return eps.mul(std).add_(mu)
    else:
        return mu

def forward(self, x):
    mu_logvar = self.encoder(x.view(-1, 784)).view(-1, 2, d)
    mu = mu_logvar[:, 0, :]
    logvar = mu_logvar[:, 1, :]
    z = self.reparameterise(mu, logvar)
    return self.decoder(z), mu, logvar

VAEの損失関数

ここでは、再構成損失（バイナリ・クロス・エントロピー）と相対エントロピー（KLダイバージェンスペナルティ）を定義します。

def loss_function(x_hat, x, mu, logvar):
    BCE = nn.functional.binary_cross_entropy(
        x_hat, x.view(-1, 784), reduction='sum'
    )
    KLD = 0.5 * torch.sum(logvar.exp() - logvar - 1 + mu.pow(2))

    return BCE + KLD

新しいサンプルの生成

モデルを訓練した後、正規分布からランダムな$z$をサンプリングし、それをデコーダーに供給します。 図6から、一部の結果が良くないことがわかります。それは、デコーダーが潜在空間全体を「カバー」していないためです。より多くのエポックでモデルを訓練すると、これを改善できます。

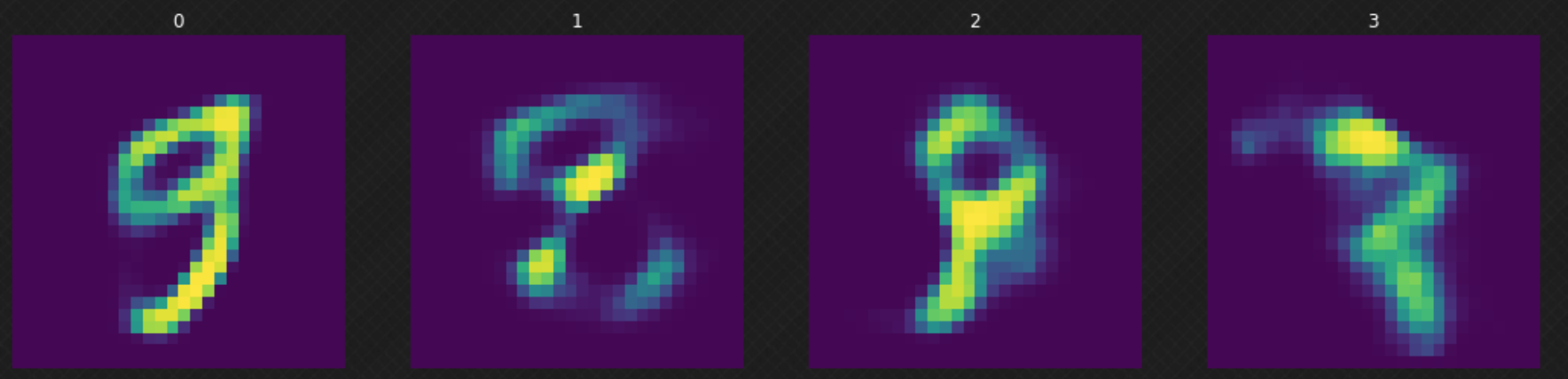
図6: 潜在空間をランダムに移動する

ある数字が別の数字にどのように変化するか（オートエンコーダを使っていたたらこれはできなかったことです）について見てみましょう。潜在空間をみてみると、デコーダーの出力はまだちゃんとしていることがわかります。 以下の図7は、数字$3$を$8$に変換する方法を示しています。

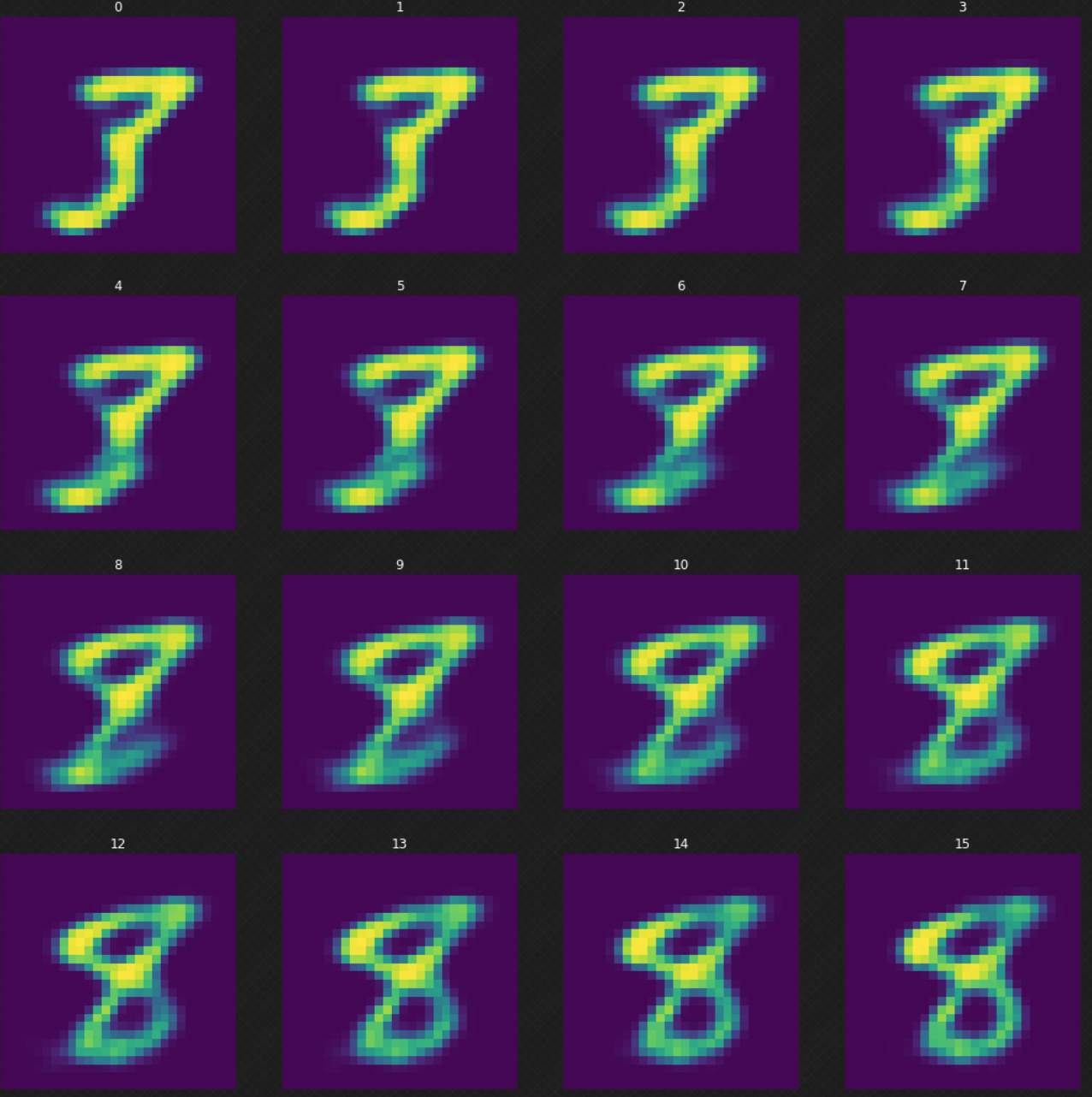
図7: 数字の3を8に変換する

平均の投射

最後に、訓練中/訓練後に潜在空間がどのように変化するかを見てみましょう。 図8の次のグラフは、2次元空間に射影されたエンコーダーの出力からの平均であり、各色は数字を表しています。エポック0では、クラスはほとんど集中せずにばらついていることがわかります。モデルが訓練されると、潜在空間がより明確になり、クラス（数字）がクラスターを形成し始めます。

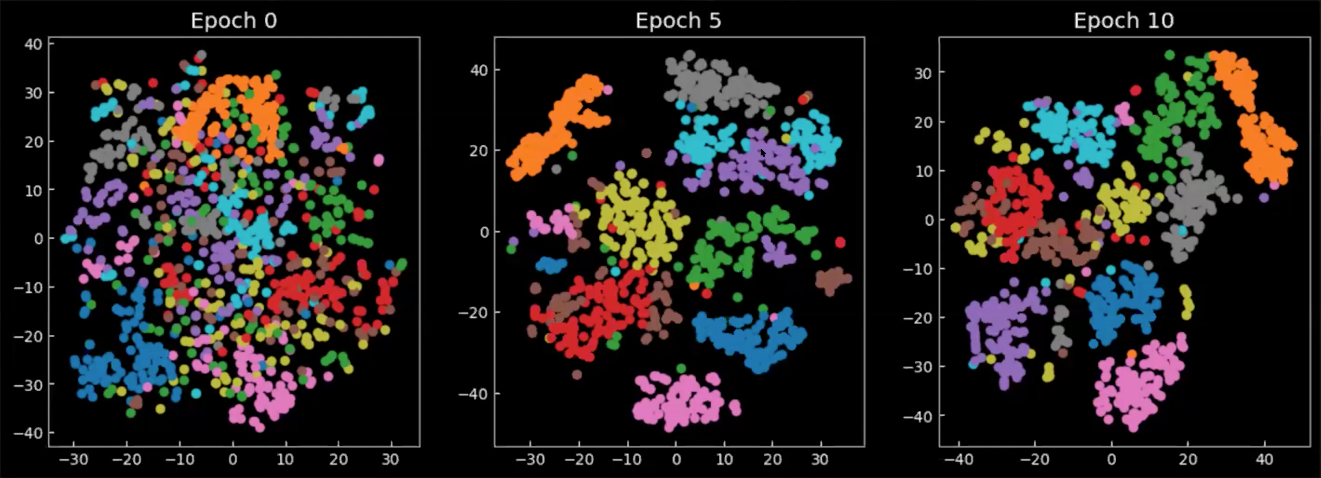
図8: 潜在空間での平均$\E(\vect{z})$の2次元射影