Regularized Latent Variable Energy Based Models
🎙️ Yann LeCun正則化された潜在変数EBM
潜在変数を含んだモデルは、観測された入力$x$と追加の潜在変数 $z$で条件づけられた予測$\overline{y}$の分布を作成できます。エネルギーベースモデル(EBM)には、潜在変数を含めることもできます。
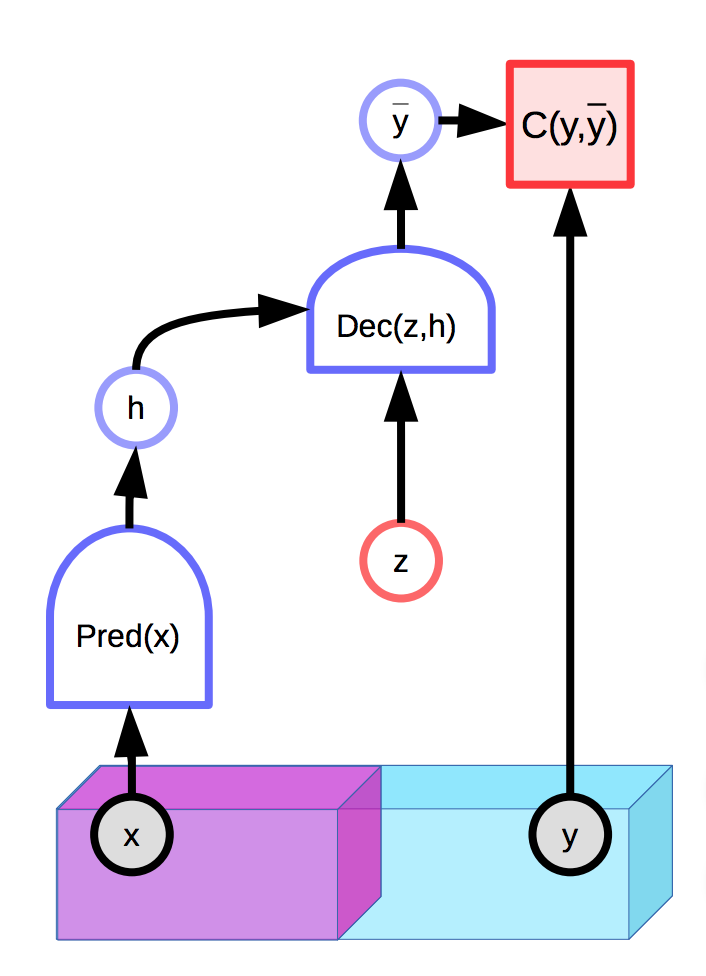
図1: 潜在変数を持つEBMの例
詳細については、前の講義のメモを参照してください。
残念なことに、潜在変数$z$が最終的な予測$\overline{y}$を生成する際に表現力が大きすぎる場合、任意の真の出力$y$は、適切に選択された$z$を使用して入力$x$から完全に再構成されてしまいます。 これは、推論中にエネルギーが$y$と$z$の両方で最適化されるため、エネルギー関数がどこでも0になってしまうということです。
自然な解決策は、潜在変数$z$の情報容量を制限することです。これを行う1つの方法は、潜在変数を正則化することです。
\[E(x,y,z) = C(y, \text{Dec}(\text{Pred}(x), z)) + \lambda R(z)\]この方法では、$z$の空間のボリュームが小さな値で制限され、その値によって、エネルギーの低い$y$の空間が制御されます。 $\lambda$の値は、このトレードオフを制御します。$R$の有用な例は、$L_1$ノルムです。これは、ほとんどどこでも微分可能な有効次元の近似計算と見なすことができます。 $L_2$ノルムを制限しながら$z$にノイズを追加すると、情報の内容(VAE)を制限することもできます。
スパースコーディング
スパースコーディングは、区分的線形関数でデータを近似しようとする無条件の正則化潜在変数EBMの例です。
\[E(z, y) = \Vert y - Wz\Vert^2 + \lambda \Vert z\Vert_{L^1}\]$n$次元ベクトル$z$は、最大数が$m « n$の非ゼロの要素を持つ傾向があります。よって、各$Wz$は、$W$の$m$列が貼る空間の要素になります。 各最適化ステップの後、行列$W$と潜在変数$z$は、$W$の列の$L_2$ノルムの合計によって正規化されます。これにより、$W$と$z$が無限大やゼロに発散しないことが保証されます。
FISTA

図2: FISTAの計算グラフ
FISTA(高速ISTA)は、2つの項$\Vert y - Wz\Vert^2$と$\lambda \Vert z\Vert_{L^1}$を交互に最適化することにより、$z$に関してスパースコーディングされたエネルギー関数$E(y, z)$を最適化するアルゴリズムです。 $Z(0)$を初期化し、次のルールに従って$Z$を繰り返し更新します。
\[z(t + 1) = \text{Shrinkage}_\frac{\lambda}{L}(z(t) - \frac{1}{L}W_d^\top(W_dZ(t) - y))\]この内側の式 $Z(t) - \frac{1}{L}W_d^\top(W_dZ(t) - Y)$は、$\Vert y - Wz\Vert^2$項についての勾配ステップです。次に、$\text{Shrinkage}$関数は、値を0へずらします。これにより、$\lambda \Vert z\Vert_{L_1}$項が最適化されます。
LISTA
FISTAは、高次元データの大規模なセット(例:画像)に適用するにはコストがかかりすぎます。それをより効率的にする1つの方法は、代わりに最適な潜在変数$z$を予測するようにネットワークを訓練することです。
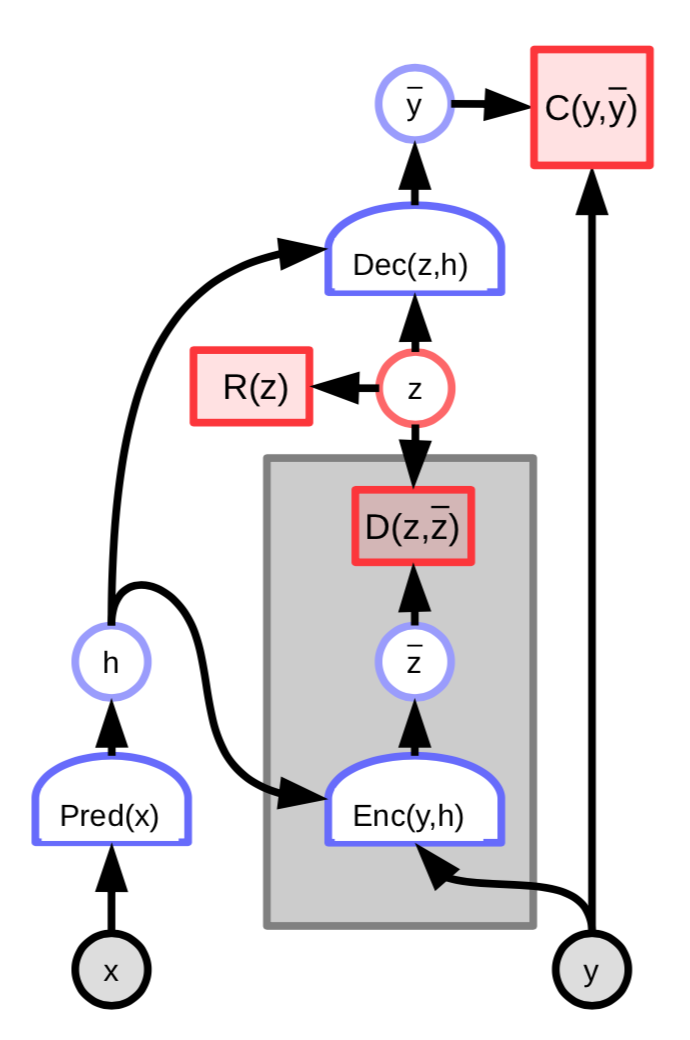
図3: 潜在変数エンコーダーを備えたEBM
このアーキテクチャのエネルギーには、予測された潜在変数$\overline z$と最適な潜在変数$z$の差を測る追加の項が含まれます。
\[C(y, \text{Dec}(z,h)) + D(z, \text{Enc}(y, h)) + \lambda R(z)\]さらに下記のように定義します
\[W_e = \frac{1}{L}W_d\] \[S = I - \frac{1}{L}W_d^\top W_d\]そして
\[z(t+1) = \text{Shrinkage}_{\frac{\lambda}{L}}[W_e^\top y - Sz(t)]\]この更新則はリカレントネットワークとして解釈できます。すなわち、潜在変数$z$を繰り返し決定するパラメーター$W_e$を代わりに学習できるということです。ネットワークは一定数のタイムステップ$K$で実行され、$W_e$の勾配は一般的な通時的誤差逆伝播法(backpropagation-through-time)を使用して計算されます。訓練されたネットワークは、FISTAアルゴリズムよりも少ないイテレーションで適切な$z$を生成します。
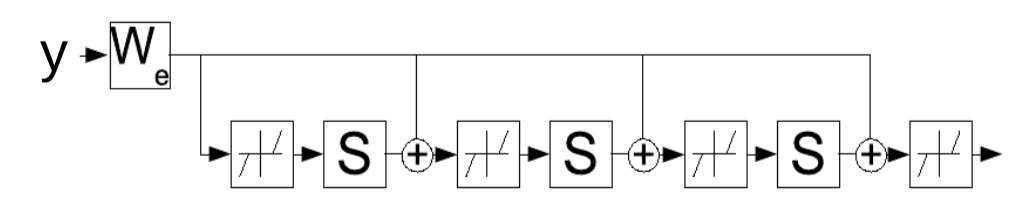
図4: 時間方向に展開されたリカレントネットとしてのLISTA
スパースコーディングの例
256次元の潜在ベクトルを持つスパースコーディングシステムがMNISTの手書き数字データセットに適用されると、システムは、その線形結合で訓練集合全体をほぼ再現できるような256の線の集合を学習します。スパース正則化により、少数の線から再現できるように保証されます。

図5: MNISTのスパースコーディング。各画像は学習され$W$の列。
スパースコーディングシステムが一般な画像をパッチでトレーニングする場合、学習される特徴は、方向付きエッジであるガボールフィルターです。これらの特徴は、動物の視覚系の入力に近い部分で学習された特徴に似ています。
畳み込みスパースコーディング
仮に画像とその画像の特徴マップ($z_1, z_2, \cdots, z_n$)があるとします。すると、各特徴マップをカーネル$K_i$で畳み込む($*$)ことができます。その結果、再構成されたものは次のように計算できます。
\[Y=\sum_{i}K_i*Z_i\]これは、再構築が$Y = \sum_{i} W_iZ_i$として実行されていた元々のスパースコーディングとは違います。通常のスパースコーディングでは、$Z_i$の係数を重みとした列の重み付き和があります。畳み込みスパースコーディングでは、それは同じく線形演算ですが、辞書行列は特徴マップになり、各特徴マップを各カーネルで畳み込んだ結果を合計することになります。
自然画像に応用した畳み込みスパースオートエンコーダ

図6 得られたフィルターと基底関数。線形畳み込みデコーダー
エンコーダーとデコーダーのフィルターは非常によく似ています。エンコーダーは、単純な畳み込みと非線形性マップと対角線レイヤーでスケーリングしたものです。すると、コードの制約にスパース性があります。デコーダーのほうは単純に畳み込み線形デコーダーであり、ここにおける再構成は二乗誤差となっています。
もし、フィルターが1つしかない場合は、中心を囲むタイプのフィルターになります。 2つのフィルターを使用すると、変な形のフィルターをいくつか取得できます。4つのフィルターを使用すると、方向付けエッジフィルター(水平および垂直)とフィルターごとに2つの極性が得られます。8つのフィルターを使用すると、8つの異なる方向で方向付けられたエッジを取得できます。16個のフィルターを使用すると、中心に沿ってより多くの方向性が得られます。フィルター数を増やしていくと、エッジ検出器に加えてより多様なフィルターが得られ、またさまざまな方向、中心としたグレーティング検出器なども得られます。
この現象は、わたしたちの視覚野で観察されていることとよく似ているため、興味深いように思われます。これで、完全に教師なしの方法で本当に優れた特徴を学習できることを示しています。
別の使用法として、これらの特徴を畳み込みネットワークに接続してから何かのトレーニングする場合、とくにイメージネットで最初からトレーニングするよりも必ずしも良い結果が得られないが、パフォーマンスの向上に役立つ場合がすぐできます。たとえば、サンプルの数が十分に多くない場合やラベル・カテゴリが少ない場合、純粋に教師ありの方法でトレーニングすると特徴が完全に解読できなくなります。

図7 カラー画像の畳み込みスパース符号化
上の図は、カラー画像の別の例です。デコードカーネル(右側)のサイズは9 x 9です。このカーネルは、画像ピクセル全体に畳み込みで適用されます。左側の画像は、エンコーダーからのスパースコードです。 $Z$ベクトルは非常に疎な空間であり、白または黒(灰色以外)の要素はほとんどありません。
変分オートエンコーダ
変分オートエンコーダは、スパース性を除いて、正則化潜在変数EBMと類似したアーキテクチャを備えています。その違いは、コードの情報内容が、ノイズを多くすることによって制限されることです。
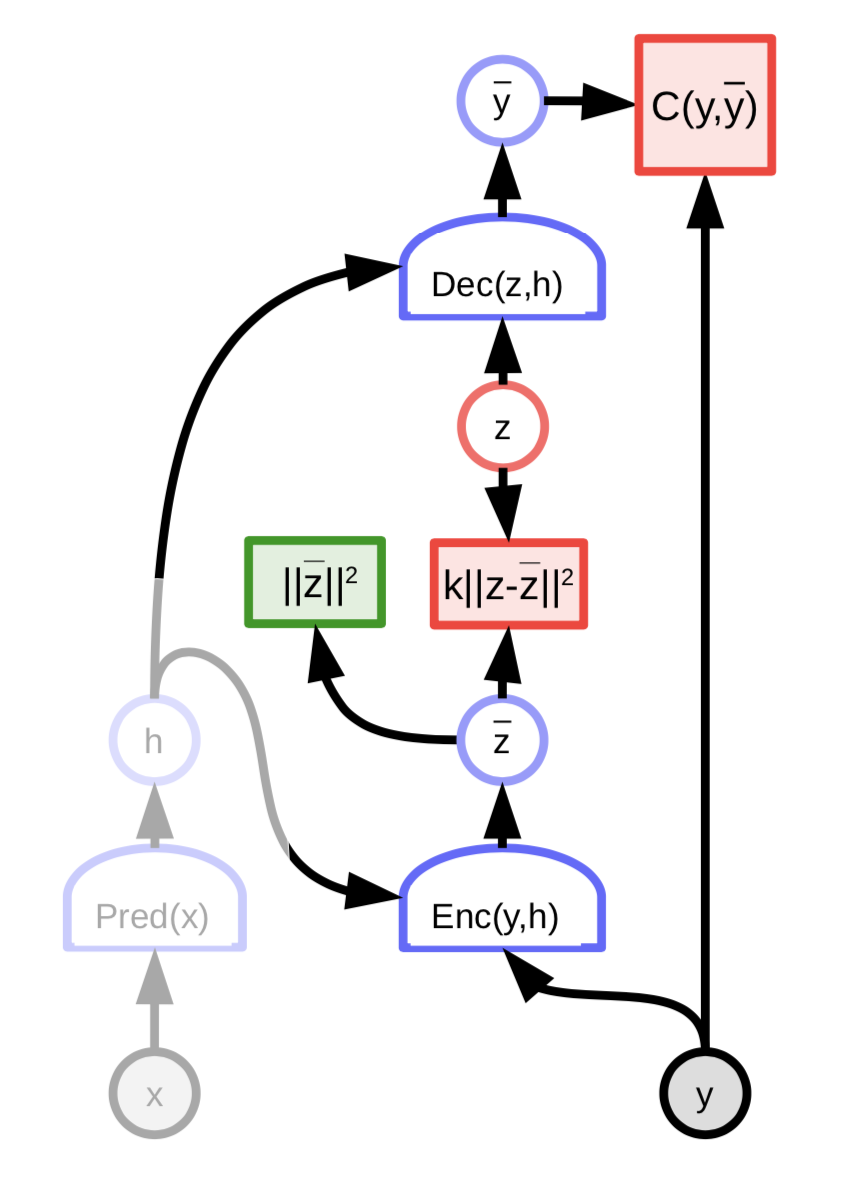
図8: 変分オートエンコーダのアーキテクチャ
潜在変数$z$は、$z$に対してエネルギー関数を最小化することで計算されるのではありません。代わりに、エネルギー関数は、その対数が${\overline z}$とリンクしたコスト関数であるような分布からランダムに$z$をサンプリングすることと見なされます。この分布は、平均が${\overline z}$のガウス分布であり、これによってガウスノイズが${\overline z}$に付加されることになります。
ガウスノイズが追加されたコードベクトルは、図9(a)に示すようにファジーボールとして可視化できます。
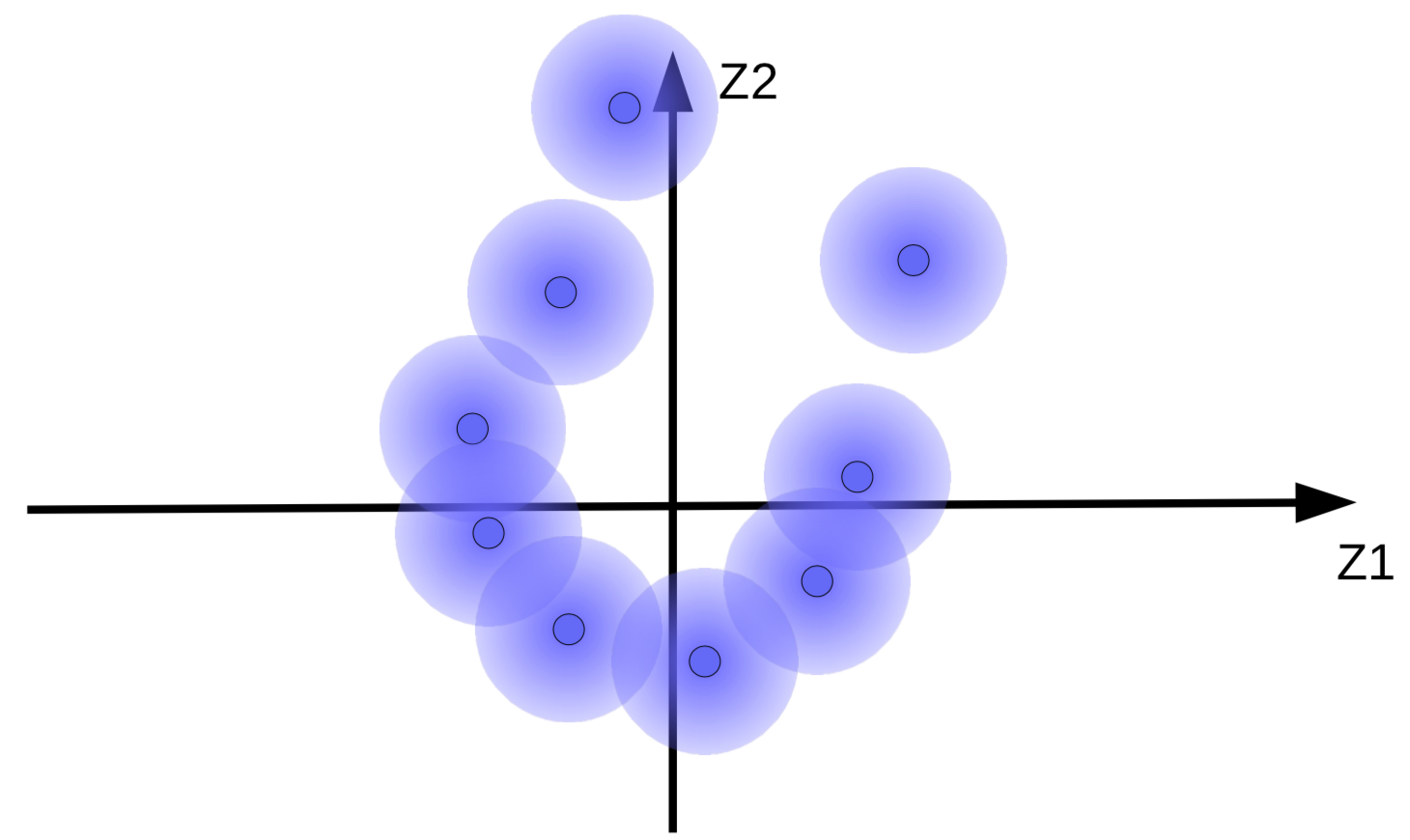 (a) 元のファジーボールの集合 |
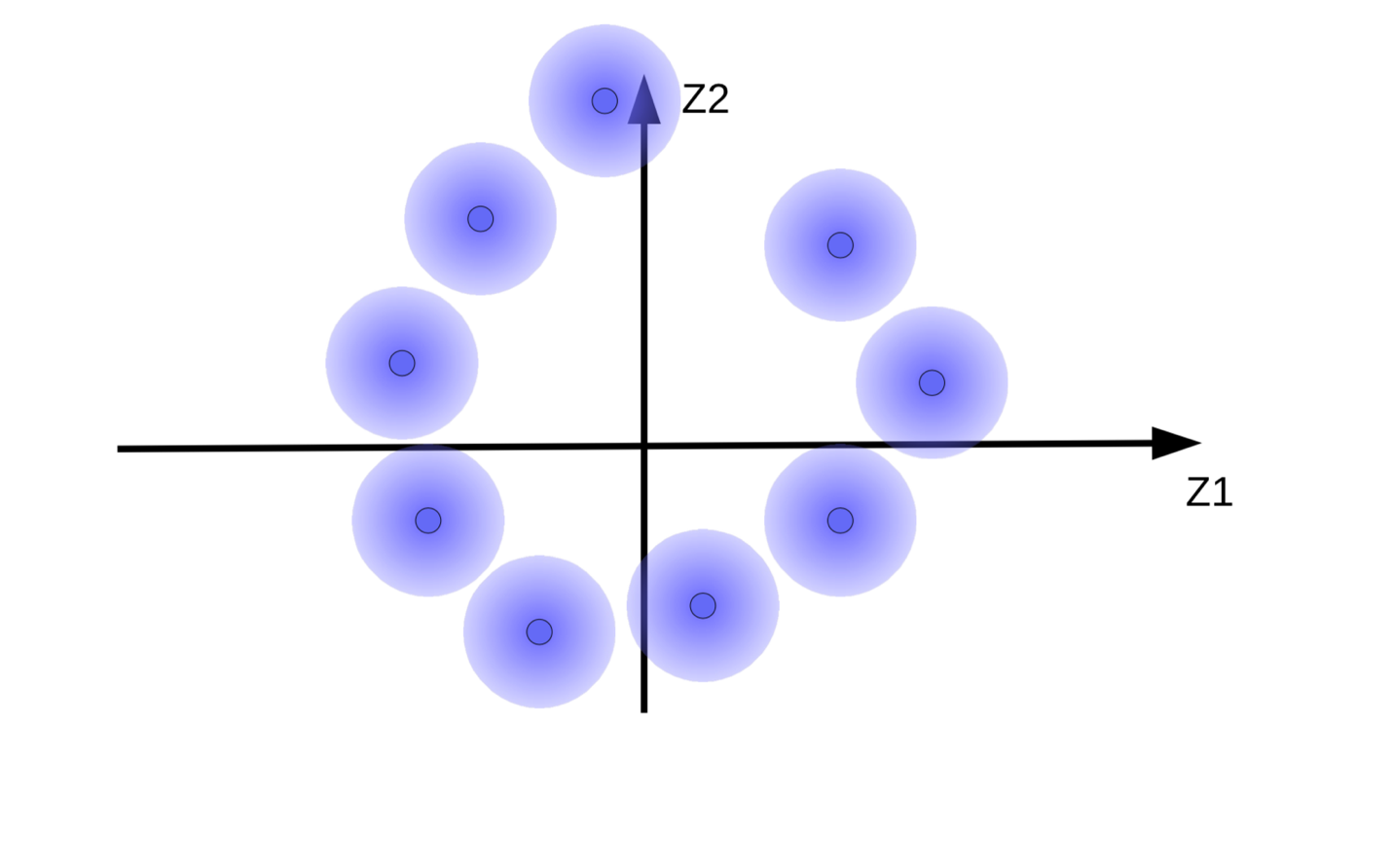 (b)正則化を加えずエネルギーを最小化することによるファジーボールの移動 |
(b)の動き正則化なしのエネルギー最小化によるファジーボール
ファジーボールに対するエネルギー最小化の効果
システムは、コードベクトル${\overline z}$をできるだけ大きくして、$z$(ノイズ)の影響をできるだけ小さくしようとします。これにより、図9(b)に示すように、ファジーボールが原点から離れて浮き上がります。システムがコードベクトルを大きくしようとするもう1つの理由は、ファジーボールのオーバーラップを防ぐためです。オーバーラップは、再構成中にデコーダーが異なるサンプル同士を混同する原因になります。
ただし、ファジーボールが存在する場合は、それがデータ多様体の周りにクラスターを形成している必要があります。したがって、コードベクトルは、平均と分散がゼロに近くなるように正則化されます。これを行うには、図10に示すように、ばねによってそれらを原点にリンクします。
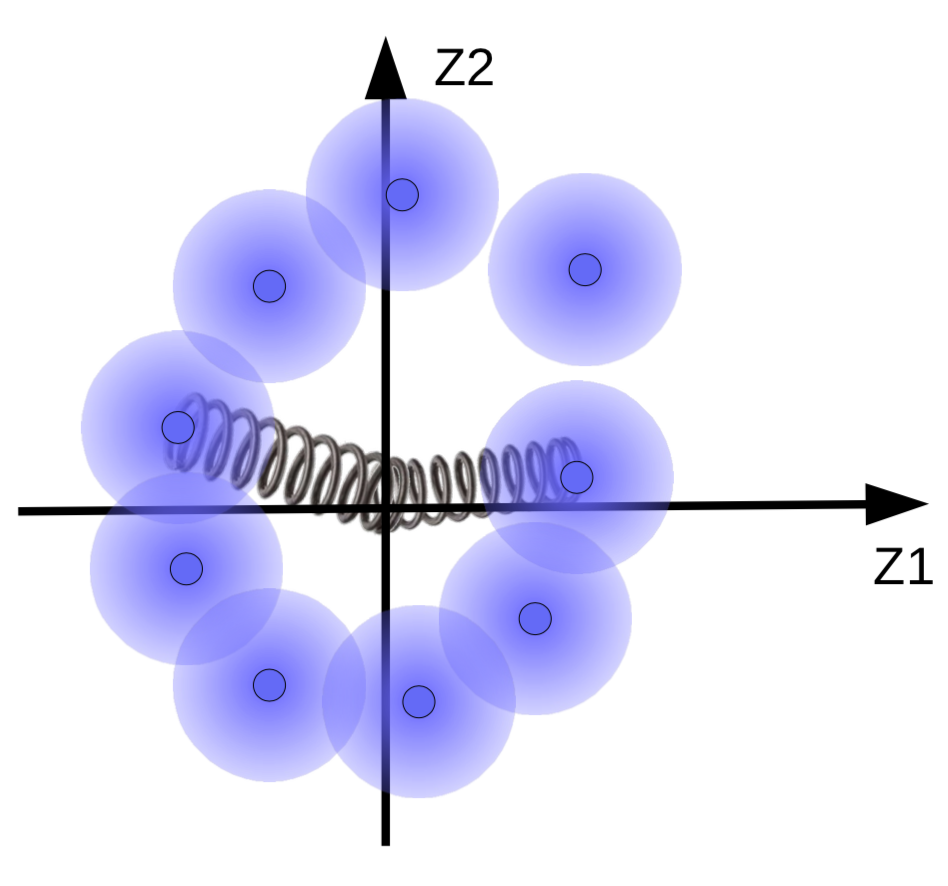
図10: バネの正則化の効果の可視化
バネの強さによって、ファジーボールが原点にどれほど近づくかが決まるようになります。バネが弱すぎると、ファジーボールが原点から飛び出し、代わりに強すぎると、原点にで崩壊し、エネルギーが高くなります。これを防ぐために、システムでは、対応するサンプルが類似している場合のみ円球を重なり合わせることになっています。
ファジーボールのサイズを調整することも可能です。これは、ペナルティ関数(KLダイバージェンス)によって分散値を1に近づけるように制限され、ボールのサイズがちょうどいいぐらいになるように調節しています。
📝 Henry Steinitz, Rutvi Malaviya, Aathira Manoj
Jesmer Wong
23 Mar 2020