Contrastive Methods in Energy-Based Models
🎙️ Yann LeCun要約
LeCun博士は、最初の約15分間で、エネルギーベースモデル(EBM)の振り返りを行いました。これに関する情報、特に対照学習法の概念については、先週の内容(第7週のメモ)を参照してください。
前回の講義で学んだように、学習方法には主に2つのクラスがあります。
- コントラスト法:訓練データ点のエネルギー$F(x_i, y_i)$を押し下げ、他のすべての点におけるエネルギー$F(x_i、y ’)$を押し上げる。
- アーキテクチャ法:正則化を適用することによって低エネルギー領域を最小化/制限するエネルギー関数$F$を構築する。
さまざまな訓練法の特徴を区別するために、LeCun博士は、前述の2つのクラスをさらに7つの訓練戦略に分類します。その1つは、データで点のエネルギーを押し下げ、他のすべてのところのエネルギーを押し上げる、つまり最尤法に似た方法です。
最尤法は、訓練データ点でエネルギーを確率的に押し下げ、他のすべての$y’ \neq y_i$である点のエネルギーを押し上げます。最尤法は、エネルギーの絶対値を「考慮する」のではなく、エネルギー間の差を「考慮する」だけです。確率分布は常に合計で1になるように正規化されているため、任意の2つのデータ点間の比率を比較する方が、単に絶対値を比較するよりも便利です。
Contrastive methods in self-supervised learning
自己教師あり学習のコントラスト的な方法
コントラスト法では、観測された訓練データ点$(x_i, y_i)$のエネルギーを押し下げ、訓練データ多様体以外の点のエネルギーを押し上げます。
自己教師あり学習では、入力の一部を使用して他の部分を予測します。自己教師あり学習によって学習されたモデルは、教師あり学習によって獲得された特徴表現に匹敵するような、コンピュータビジョンのための良い表現を生み出すことが期待されます。
研究者たちは、コントラスティブな埋め込み方法を自己教師あり学習モデルに適用すると、教師ありモデルに匹敵する優れたパフォーマンスが得られることを実験的に発見しました。これらの方法とその結果を以下で説明します。
コントラスティブな埋め込み
画像$x$と、$x$の内容を保持できるような変換(回転、倍率、トリミングなど)$y$のペア($x$、$y$)について考えてみましょう。これはポジティブペアと呼びます。

図1: ポジティブペア
概念的には、コントラスティブな埋め込み法は畳み込みネットワークを使用し、$x$と$y$を入力してこのネットワークを介して$h$と$h’$の2つの特徴ベクトルを取得します。$x$と$y$の内容は同じであるため(つまりポジティブペア)、それらの特徴ベクトルをできるだけ類似させたいと考えます。 その結果、類似度の指標(コサイン類似度など)と$h$と$h’$の間の類似度を最大化するような損失関数を選択します。これで、訓練データ多様体上の画像のエネルギーを押し下げることができます。

図2: ネガティブペア
ただし、この多様体以外の点のエネルギーも押し上げる必要があります。そのため、ネガティブサンプル ($x_{\text {neg}}$, $y_{\text{neg}}$)、異なったコンテンツ(異なるクラスラベルなど)の画像も生成します。これらを上記のネットワークに入力し、特徴ベクトル$h$と$h ‘$を取得して、それらの間の類似性を最小限に抑えようとします。
この方法では、類似したペアのエネルギーを押し下げながら、異なるペアのエネルギーを押し上げることができます。
最近の結果(ImageNetについての結果)は、この方法が、教師ありで学習した特徴に匹敵する、オブジェクト認識に適した特徴を生成できることを示しています。
自己教師ありの結果(MoCo、PIRL、SimCLR)
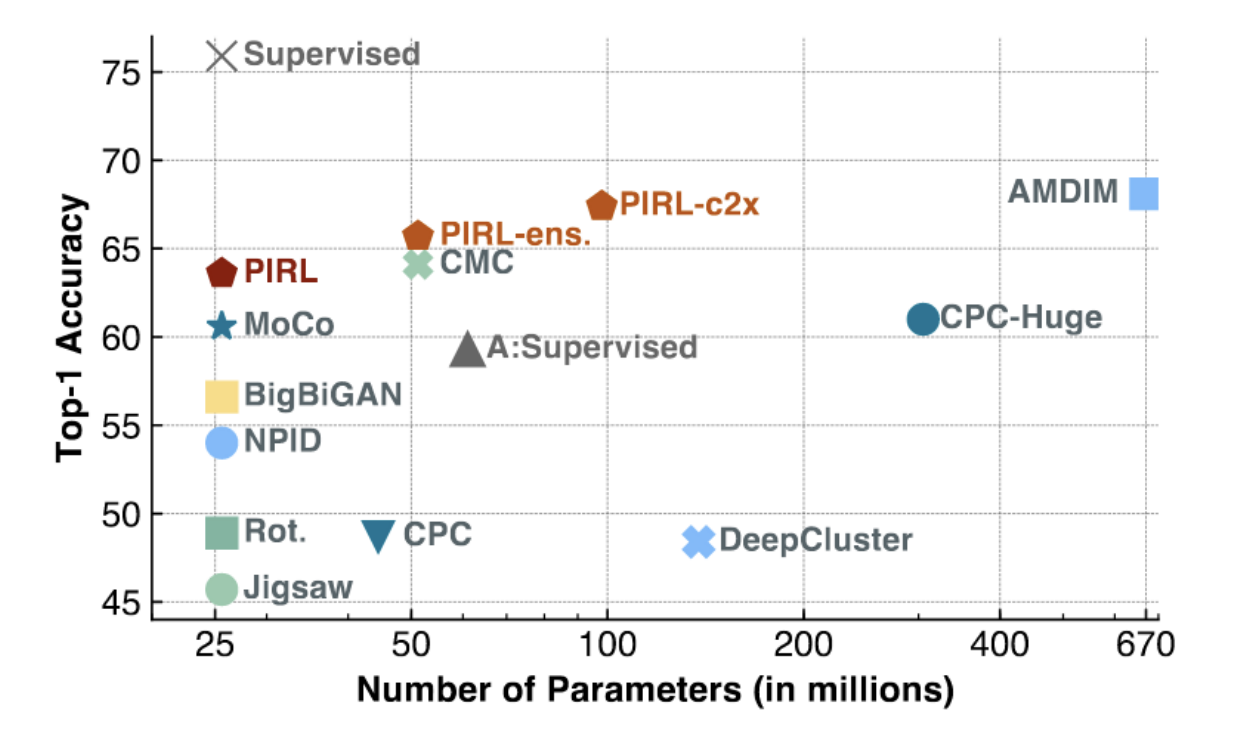
図3: ImageNetに対するPIRLとMoCo
上の図に示されているように、MoCoとPIRLはSOTAの結果を達成します(特に、パラメーターの数が少ないスケールが小さいモデルで使う場合)。 PIRLは、教師ありで学習したベースラインの上位1の線形精度(〜75%)に近づき始めています。
PIRLは、その目的関数を見ることで理解することができます。損失関数であるNCE(ノイズコントラスティブ推定量)は次のように定義されます。
\[h(v_I,v_{I^t})=\frac{\exp\big[\frac{1}{\tau}s(v_I,v_{I^t})\big]}{\exp\big[\frac{1}{\tau}s(v_I,v_{I^t})\big]+\sum_{I'\in D_{N}}\exp\big[\frac{1}{\tau}s(v_{I^t},v_{I'})\big]}\] \[L_{\text{NCE}}(I,I^t)=-\log\Big[h\Big(f(v_I),g(v_{I^t})\Big)\Big]-\sum_{I'\in D_N}\log\Big[1-h\Big(g(v_{I^t}),f(v_{I'})\Big)\Big]\]ここでは、2つの特徴マップ/ベクトル間の類似度の指標を、コサイン類似度で定義しています。
PIRLが通常の学習と異なる点は、畳み込み抽出抽出器の出力を直接は使用しないことです。代わりに、異なる heads $f$と$g$を定義します。これらは、畳み込み特徴抽出器の上にある独立な層だと考えることができます。
すべてをまとめると、PIRLのNCE目的関数は次のように機能します。ミニバッチでは、1つのポジティブ(類似した)ペアと多くのネガティブ(異なる)ペアがあります。次に、ミニバッチ内の変換された画像の特徴ベクトル($I^t$)と残りの特徴ベクトル(1つは正、残りは負)の間の類似度を計算します。次に、ポジティブペアのソフトマックスのような関数のスコアを計算します。ソフトマックススコアを最大化することは、残りのスコアを最小化することと同じであり、これはエネルギーベースモデルに必要なことです。したがって、最終的に得られた損失関数によって、類似したペアでエネルギーを押し下げ、異なるペアでエネルギーを押し上げるモデルを構築することができます。
LeCun博士は、これを機能させるには、多数のネガティブサンプルが必要であると述べています。 SGDでは、ミニバッチからこれらのネガティブサンプルを一貫して維持することが難しい場合があります。したがって、PIRLはキャッシュされたメモリバンクも使用します。
質問: なぜL2-ノルムよりコサイン類似度を使用するのですか? 回答:L2ノルムは、ベクトル間の部分差の2乗の合計にすぎないため、2つのベクトルを「短く」(中心に近く)することで類似させることや、2つのベクトルを非常に「長く」(中心から遠く)することで類似させないようにすることが非常に簡単にできてしまいます。したがって、コサイン類似度を使用することで、システム上、ベクトルを短くしたり長くしたりするといった「ずる」をせずに適切な解を見つけることができます。
SimCLR
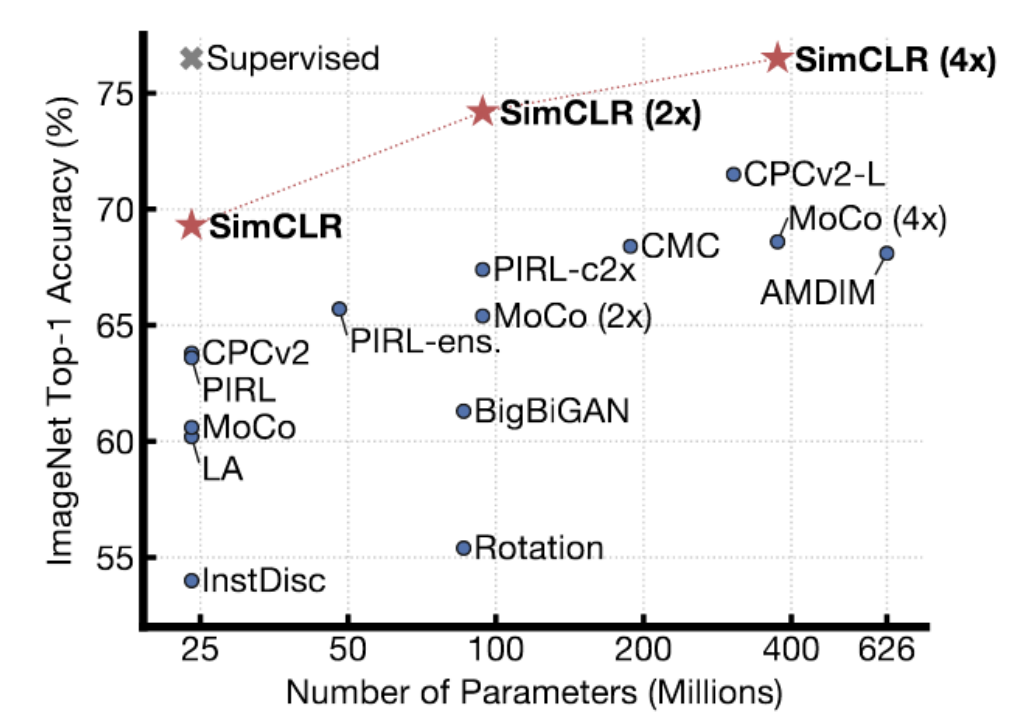
図4: ImageNetについてのSimCLRの結果
SimCLRは、上記の方法よりも優れた結果が達成できます。これは、ImageNetについて教師あり学習方法を用いた時のパフォーマンスに達し、ImageNetの線形精度はトップ1になります。この手法では、高度なデータ拡張方法を使用して類似したペアを生成し、TPUで長時間(非常に大きなバッチサイズで)訓練を行います。
LeCun博士は、SimCLRがある程度コントラスティブな方法の限界を示している、と信じています。高次元空間には、データ多様体よりも実際に確実にエネルギーが高くなるようにエネルギーを押し上げる必要がある多くの領域があります。また、表現の次元を増やせば増やすほど、多様体上にない場所でエネルギーが高くなるようにするため、多くのネガティブサンプルが必要になります。
デノイジングオートエンコーダー
先週の講義で、デノイジングオートエンコーダーについて説明しました。このモデルは、破損した入力から元の入力を再構成することにより、データの表現を学習する傾向があります。特に、破損したデータがデータ多様体から離れるにつれて二次関数的に増加するようなエネルギー関数を生成するようにそのシステムを訓練します。
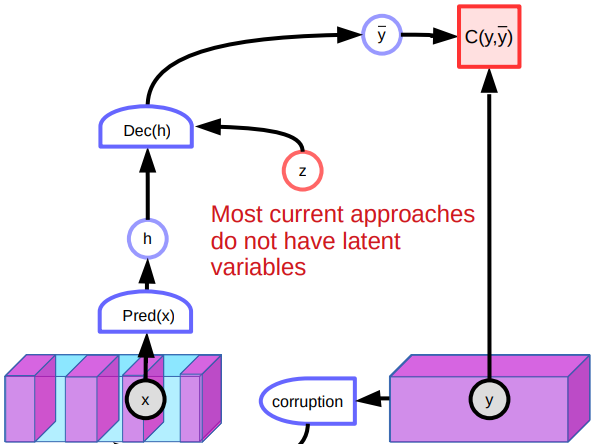
図5: デノイジングオートエンコーダーのアーキテクチャ
問題
ただし、デノイジングオートエンコーダーにはいくつかの問題があります。 1つの問題は、高次元の連続空間では、データの一部を破損する無数の方法があることです。したがって、さまざまな場所を押し上げるだけではエネルギー関数を形成できるという保証はありません。
もう1つの問題は、潜在変数がない画像を処理するときにパフォーマンスが低下することです。画像を再構成する方法はたくさんあるので、システムはさまざまな予測を生成し、特に優れた特徴を学習しません。
さらに、多様体の中央にある破損した点は、両側に再構成できます。これにより、エネルギー関数に平坦な場所が生み出され、全体的なパフォーマンスに影響します。
他のコントラスティブな方法
コントラスティブダイバージェンス法、比率マッチング、Noise-Contrastive Estimation、minimum probability flow法など、他のコントラスティブ法があります。ここでコントラスティブダイバージェンス法の基本的な考え方について簡単に説明します。
コントラスティブダイバージェンス法
コントラスティブダイバージェンス法(CD法)は、入力サンプルをうまく破損することによって表現を学習する別のモデルです。連続空間では、最初に訓練サンプル$y$を選択し、そのエネルギーを下げます。そのサンプルでは、ある種の勾配ベースのプロセスを使用して、ノイズとともにエネルギーを押し下げます。入力空間が離散的である場合、代わりに訓練サンプルをランダムに摂動させてエネルギーを変更できます。得るエネルギーが低ければ維持して、そうでなければ、ある程度の確率で破棄します。
これをやり続けると、最終的に$y$のエネルギーを低下することができます。次に、$y$と対照的なサンプル$\bar y$をある損失関数で比較することにより、エネルギー関数のパラメーターを更新することができます。
持続的なコントラスティブダイバージェンス法
コントラスティブダイバージェンス法(CD法)を改良したものの一つとして、持続的なコントラスティブダイバージェンス法があります。システムは一連の「粒子」を使用し、それらの位置を記憶します。これらの粒子は、通常のCD法で行ったのと同じように、エネルギー面を下に移動します。最終的に、この粒子らはエネルギー面で低エネルギーの場所を見つけ、それらを押し上げさせます。ただし、システムは次元の増加に対して適切にスケールしません。
📝 Vishwaesh Rajiv, Wenjun Qu, Xulai Jiang, Shuya Zhao
Jesmer Wong
23 Mar 2020