オートエンコーダーの紹介

オートエンコーダーの応用

画像の生成

図1でどちらの顔が偽物かわかりますか？実は、どちらもStyleGan2のジェネレーターによって生成されています。顔の細部は非常にリアルですが、背景が不気味に見えます（左：ぼやけている、右：形が崩れている）。これは、ニューラルネットワークが顔のサンプルで訓練されているためです。そのため、背景のばらつきが大きくなります。ここでは、データ多様体は、顔画像の自由度に相当する約50の次元を持っています。

図. 1: StyleGan2で生成された顔画像

ピクセル空間と潜在空間における補間の違い

図2: 犬と鳥

犬画像（図２）と鳥画像（図２）をピクセル空間で線形補間すると、図３のように２つの画像が半透明になり重なり合ったような画像が得られます。左上から右下に向かって、犬画像の重さが減少し、鳥画像の重さが増加していることがわかります。

図3: 補完した結果

2つの潜在空間での表現を補間してデコーダに与えると、図4のような犬から鳥への変換が得られます。

Fig. 4:デコーダーに入力した結果

明らかに、画像の構造を捉えるには、潜在空間の方が優れていることがわかります。

変換の例

図5: 拡大

図6: 平行移動

図7: 明度

図8: 回転 (回転は3次元になる可能性があることに注意してください。)

画像の超解像

このモデルは、画像をアップスケールして元の顔を再構成することを目的としています。図9の左から右へ、最初の列は16x16の入力画像、2番目の列は標準的な二重曲線補間から得られるもの、3番目はニューラルネットによって生成された出力、そして右は実際の画像です(https://github.com/david-gpu/srez)。

図9: 元の顔の再構成

出力画像を見ると、学習データに偏りがあり、それが再構成された顔を不正確なものにしていることがわかります。例えば、左上のアジア人男性の顔は、学習画像のバランスが悪いため、出力画像ではヨーロッパ人に見えてしまいます。左下の女性の再構成された顔は、訓練データにこのような変な角度からの画像がないために不気味に見えてしまいます。

画像の修復

図10: 灰色のパッチを顔に当てる

図10のように顔に灰色のパッチを当てることで、訓練データの多様体から画像を遠ざけることができます。図11の顔の再構成は、エネルギー関数の最小化を介して、訓練データの多様体上で最も近いサンプル画像を見つけることによって行われます。

図11: 再構成された図10の画像

画像のキャプション

図12: 画像の例へのキャプション

図12のテキストによる記述から画像への変換は、重要な視覚の情報に関連付けられたテキストの特徴表現を抽出し、それを画像にデコードすることで実現されます。

オートエンコーダーとは？

オートエンコーダーは、教師なしで訓練されるニューラルネットワークであり、最初にデータの符号化された表現を学習し、学習した符号化された表現から入力データを（可能な限り忠実に）生成することを目的としています。したがって、オートエンコーダーの出力は入力に対する予測です。

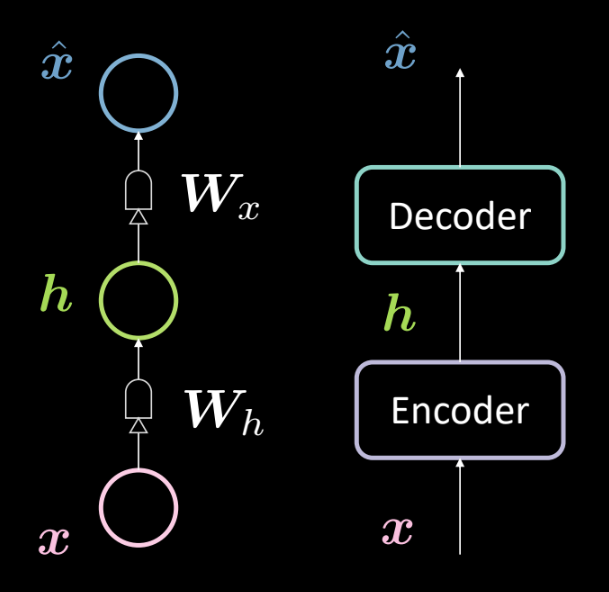
図13: 基本的なオートエンコーダーのアーキテクチャ

図 13 に基本的なオートエンコーダーのアーキテクチャを示します。先ほどと同じように、下層から入力された $\boldsymbol{x}$ をエンコーダ（$\boldsymbol{W_h}$ で定義されたアフィン変換とその後のsquashing関数）にかけます。これにより、中間の隠れ層 $B\boldsymbol{h}$ が得られます。これをデコーダ($\boldsymbol{W_x}$で定義された別のアフィン変換と別のsquashing関数)にかけます。これが出力 $\boldsymbol{\hat{x}}$ であり，これが入力の予測/再構成です。私たちの慣例では、これは３層のニューラルネットワークであると言います。

このネットワークは数学的には次のように表現されます。

また、以下のように次元を指定します。

注: PCAを表現するためには、タイトウエイト（またはタイドウエイト）を $\boldsymbol{W_x}\ \dot{=}\ \boldsymbol{W_h}^\top$で定義します。

なぜオートエンコーダーを使うのか？

この時点で、入力を予測することに何の意味があるのか、オートエンコーダーの用途は何かと疑問に思うかもしれません。

オートエンコーダーの主な用途は、異常検知や画像のノイズ除去です。オートエンコーダーのタスクは、多様体上に存在するデータを再構成することであることを見てきました。つまり、データ多様体が与えられている場合、オートエンコーダーにはその多様体に存在する入力のみを再構成できるようにしてほしいと考えています。このようにして、モデルは訓練中に観察されたものを再構成するように制約され、それによって新しい入力に存在する摂動に対して頑健になるので、そのような変動は除去されます。

オートエンコーダーのもう1つの用途は、画像圧縮です。入力の次元数 $n$ よりも低い中間次元数 $d$ があれば、エンコーダは圧縮機として使用でき、潜在表現（符号化された表現）は、より少ないスペースで特定の入力に含まれる情報のすべて（または大部分）を扱うことができます。

再構成誤差

ここで、一般的に使われる再構成損失を見てみましょう。データセットの全体的な損失は、サンプルあたりの損失の平均、で与えられます。すなわち

入力がカテゴリカルな場合、クロスエントロピー損失を使用して、次式で与えられるサンプルあたりの損失を計算することができます。

また、入力が実数値である場合、次式で与えられる平均二乗誤差損失を使用したい場合があります。

アンダーコンプリート/オーバーコンプリートな隠れ層

隠れ層の次元数 $d$ が入力の次元数 $n$ よりも小さいときは、アンダーコンプリートな隠れ層と呼ぶことにします。また、同様に、 $d>n$ の場合は、オーバーコンプリートな隠れ層と呼ぶことにします。図14は、左がアンダーコンプリートな隠れ層、右がオーバーコンプリートな隠れ層を示しています。

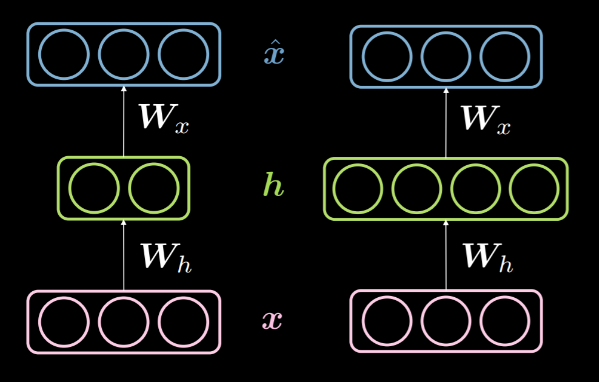
図14: アンダーコンプリートな隠れ層 vs オーバーコンプリートな隠れ層

上述したように，アンダーコンプリートな隠れ層は入力からの情報をより少ない次元で符号化しているため、情報の圧縮に用いることができます。一方で、オーバーコンプリートな隠れ層では、入力よりも高い次元での符号化を行います。これにより、最適化が容易になります。

入力を再構成しようとしているので、モデルは入力の特徴をすべて隠れ層にコピーして出力として渡す傾向があり、本質的には恒等写像のように振る舞うことになります。これは、モデルが何も学習していないことを意味するので、避ける必要があります。したがって、information bottleneckを適用して、追加の制約を適用する必要があります。これは、隠れ層がとりうる表現を、学習中に見られるものだけに制限することによって行います。これにより、選択的な再構成（入力空間の部分空間に限定されます）が可能になり、モデルは多様体に無いすべての入力に対して反応しづらくなります。

アンダーコンプリートな隠れ層は入力をコピーするのに十分な次元を持たないため、恒等写像として振る舞うことができないことに注意する必要があります。したがって、アンダーコンプリートな隠れ層は、オーバーコンプリートな隠れ層に比べて過学習する可能性が低くはなりますが、それでもまだ過学習する可能性があります。例えば、強力なエンコーダとデコーダが与えられた場合、モデルは各データポイントに1つの数値を単純に関連付け、その写像を学習することができます。過学習を回避する方法は、正則化法、アーキテクチャ法などいくつかあります。

デノイジングオートエンコーダー

図15は、デノイジングオートエンコーダーの多様体とそれがどのように機能するかを直観的に示した図です。

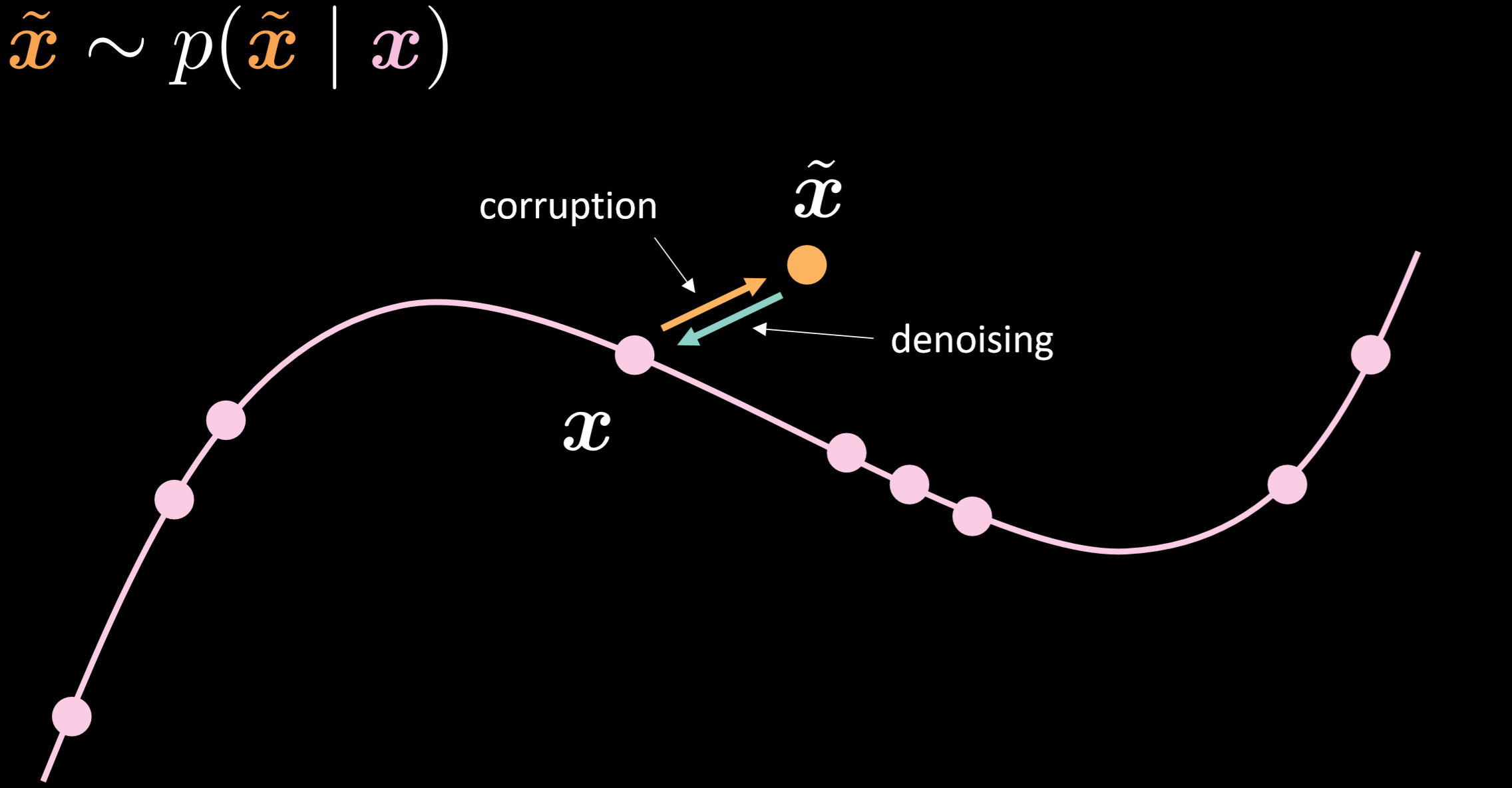
図15: デノイジングオートエンコーダー

このモデルでは、現実に観測されるようなノイズの多い分布を入力していると仮定して、そこからロバストにデータを復元する方法を学習します。 入力データと出力データを比較すると、既に多様体上にある点は動かず、多様体から離れた点は大きく動いていることがわかります。

図16は、入力データと出力データの関係を示したものです。

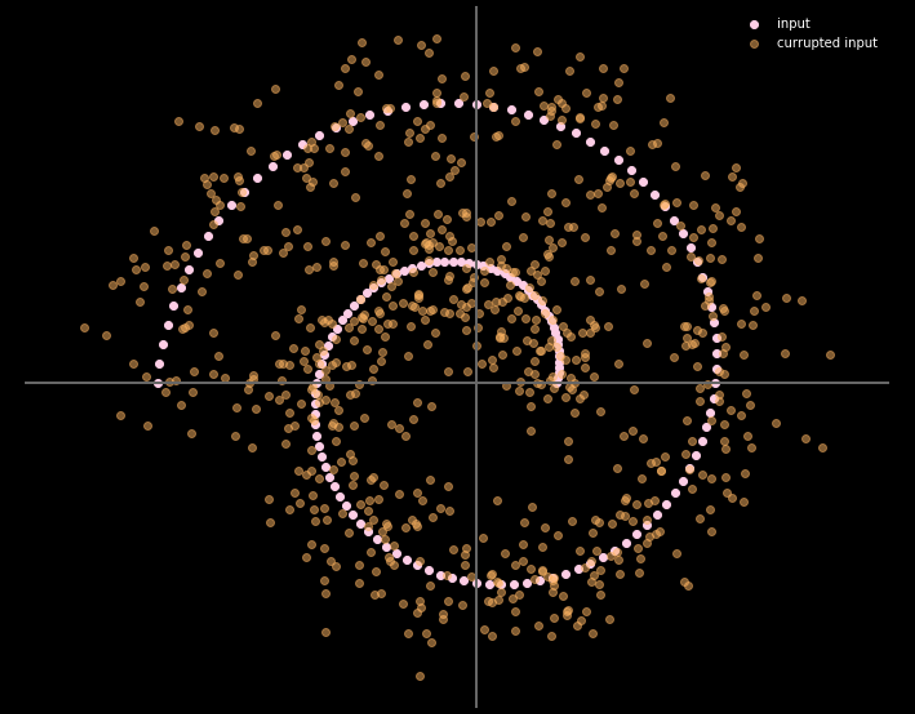
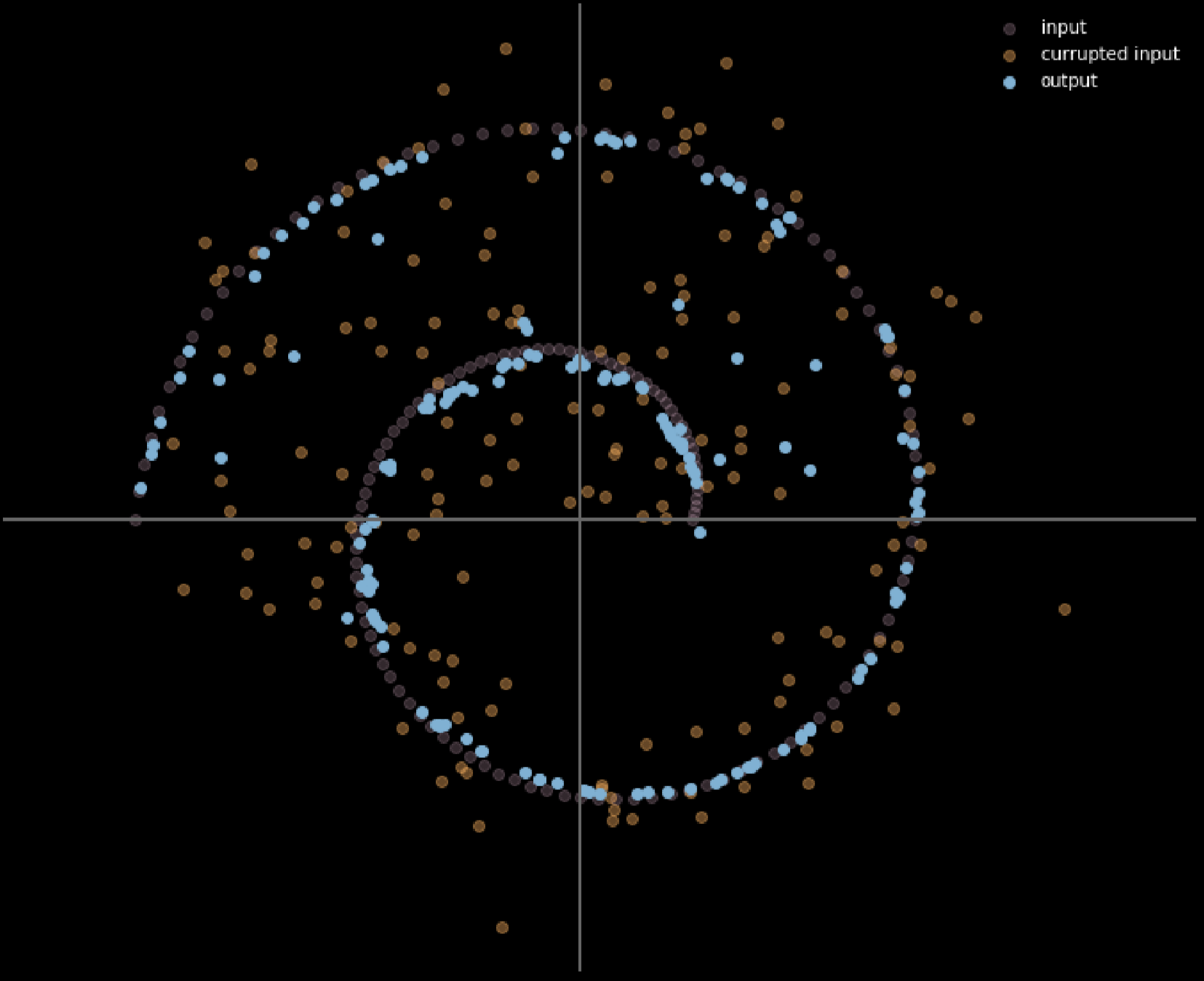
図16: デノイジングオートエンコーダーの入力と出力

また、各入力点の移動距離を表すために異なる色を使用することも可能であり、図17はそれを図示したものです。

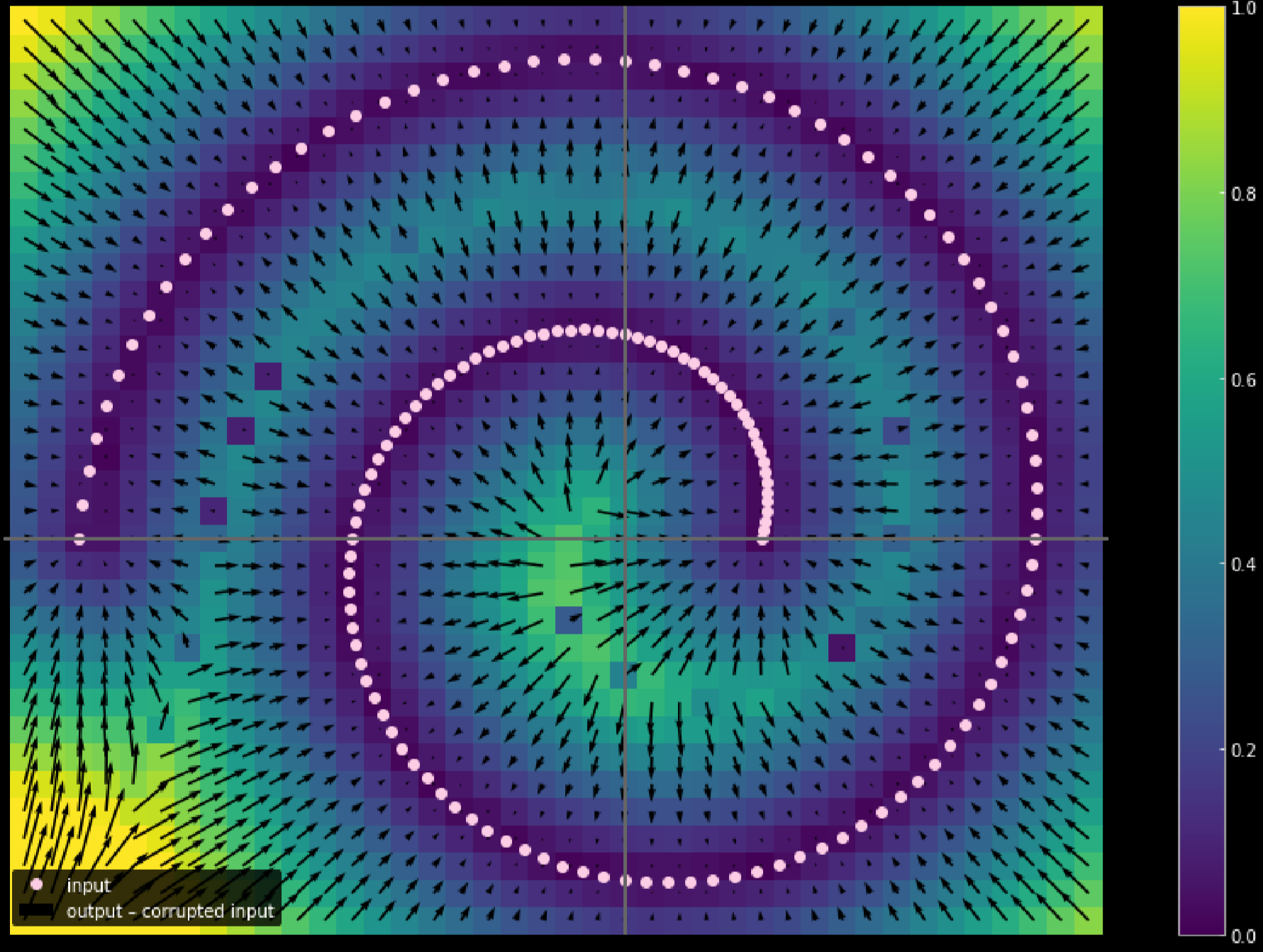
図17: 入力データが移動した距離を測ったもの

色が薄いほど移動距離が長いことを示しています。この図から、角にある点大体1単位分の距離を移動しているのに対し、2本の枝の中にある点は上と下の枝に学習中に引き込まれてしまって全く移動していないことがわかります。

縮小オートエンコーダー

図18は、縮小オートエンコーダーの損失関数とその多様体を示した図です。

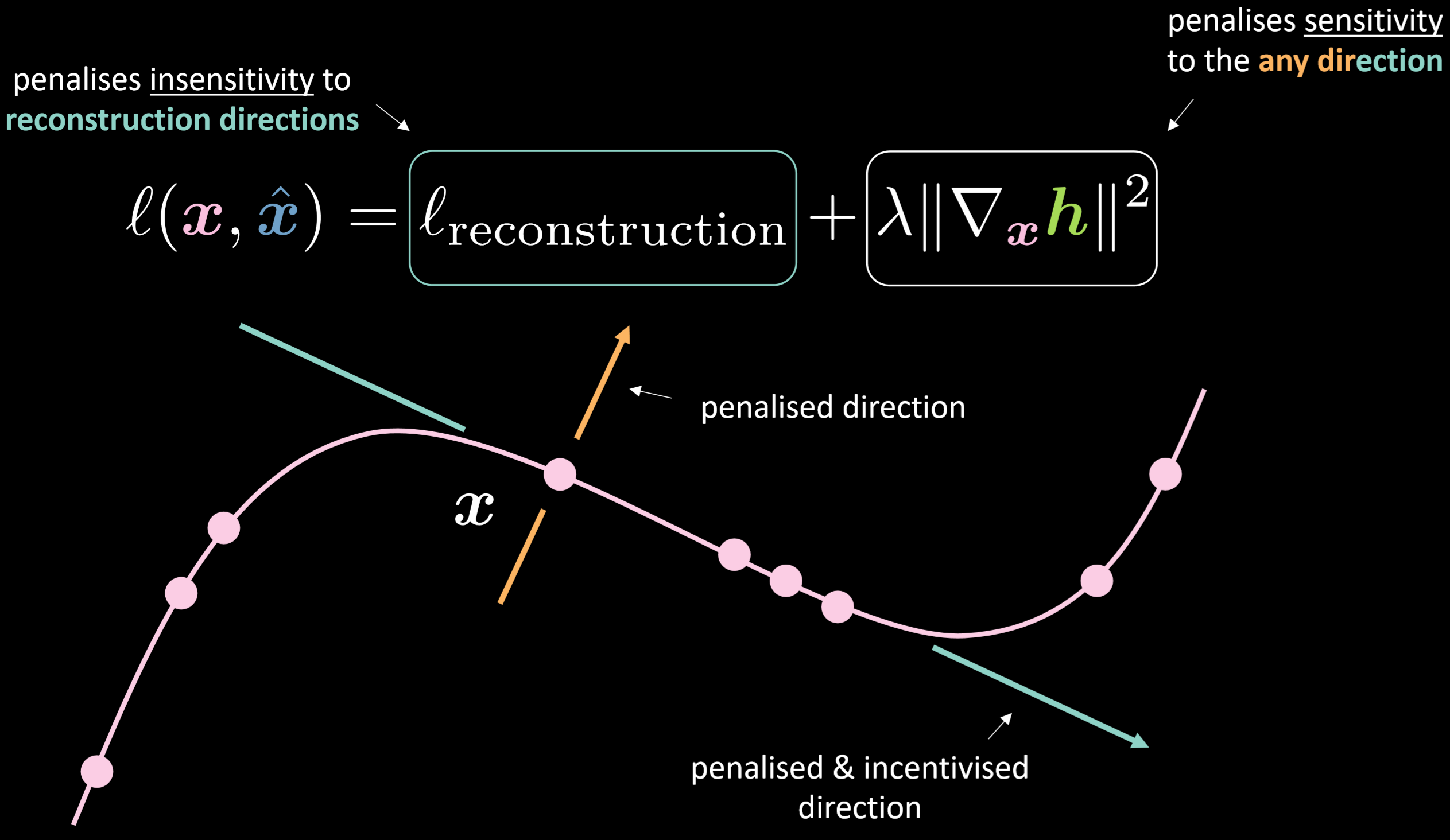
図18: 縮小オートエンコーダー

損失関数は，再構成項に入力に対する潜在表現の勾配のノルムの2乗を加えたものです。したがって、全体の損失は、入力の変動が与えられた場合の隠れ層の変動を最小化します。その利点としては、モデルが再構成に敏感になる一方で、他の可能性のある方向には鈍感になることが挙げられます。

図19は、これらのオートエンコーダーが一般的にどのように動作するかを示しています。

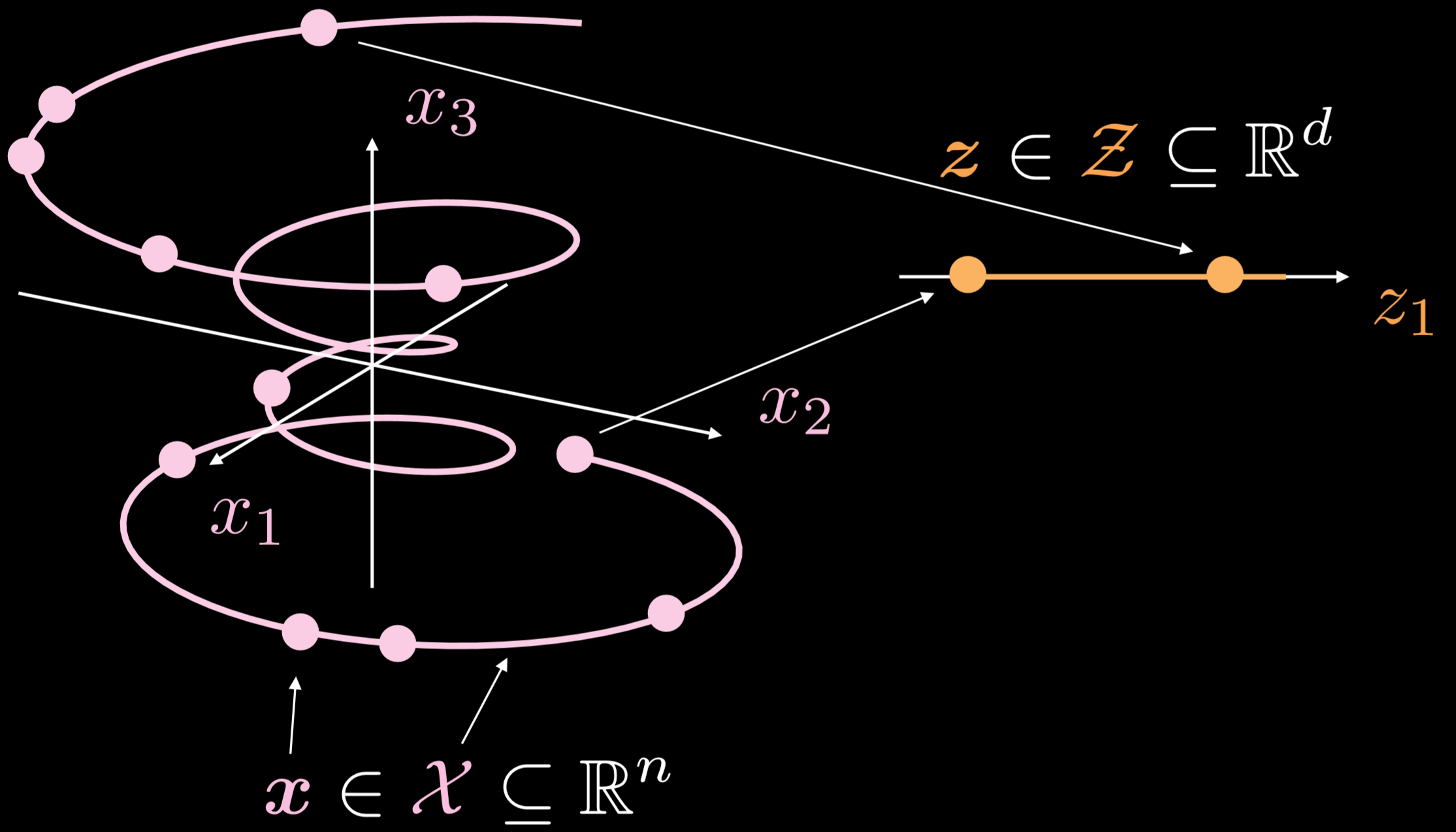
図19: 基本的なオートエンコーダー

訓練データのなす多様体は、三次元中に伸びる一次元の物体です。$\boldsymbol{x}\in \boldsymbol{X}\subseteq\mathbb{R}^{n}$であるとき、オートエンコーダーの目的は、この巻き上がった線を一方向に引き伸ばすことです。ただし、$\boldsymbol{z}\in \boldsymbol{Z}\subseteq\mathbb{R}^{d}$です。その結果、入力層の点は、隠れ層の点に変換されます。これで、入力空間上の点と潜在空間上の点の対応関係はわかりましたが、入力空間の領域と潜在空間の領域の対応関係はわかりません。その後、デコーダを利用して隠れ層の点を変換することで、意味のある出力層を生成します。

オートエンコーダーの実装 - Notebook

Jupyter Notebook はここにあります。

このnotebookでは、標準的なオートエンコーダーとデノイジングオートエンコーダーを実装して、その出力を比較します。

オートエンコーダーのアーキテクチャと再構成誤差の定義

$28 \times 28$の画像と 30次元の隠れ層を使うと 全体の変換は、$784\to30\to784$という変換になります。エンコーダとデコーダにtanh関数を適用することで、出力範囲を$(-1, 1)$に制限することができます。このモデルの損失関数には、平均二乗誤差(MSE)損失を使用します。

class Autoencoder(nn.Module):
    def __init__(self):
        super().__init__()
        self.encoder = nn.Sequential(
            nn.Linear(n, d),
            nn.Tanh(),
        )
        self.decoder = nn.Sequential(
            nn.Linear(d, n),
            nn.Tanh(),
        )

    def forward(self, x):
        x = self.encoder(x)
        x = self.decoder(x)
        return x

model = Autoencoder().to(device)
criterion = nn.MSELoss()

標準的なオートエンコーダーの学習

PyTorchで標準的なオートエンコーダーを学習するためには、次の5つの方法を訓練のループに入れる必要があります。

フォワード処理:

1) output = model(img)を呼ぶことで、入力画像をモデル内で順伝播させます
2) 次のコードで損失を計算します: criterion(output, img.data)

バックワード処理:

3) 勾配の値を溜め込まないように勾配を消去します: optimizer.zero_grad()
4) 誤差逆伝播: loss.backward()
5) 重みの更新: optimizer.step()

図20は、標準的なオートエンコーダーの出力を示した図です。

図20: 標準的なオートエンコーダの出力

デノイジングオートエンコーダーの学習

デノイジングオートエンコーダーについては，次のステップを加える必要があります:
1) nn.Dropout()でランダムにニューロンを落とす。
2) ノイズのマスクを作る: do(torch.ones(img.shape))
3) 二値マスクに良い画像を掛け合わせて悪い画像を作成する: img_bad = (img * noise).to(device).

図21はデノイジングオートエンコーダーの出力を表しています。

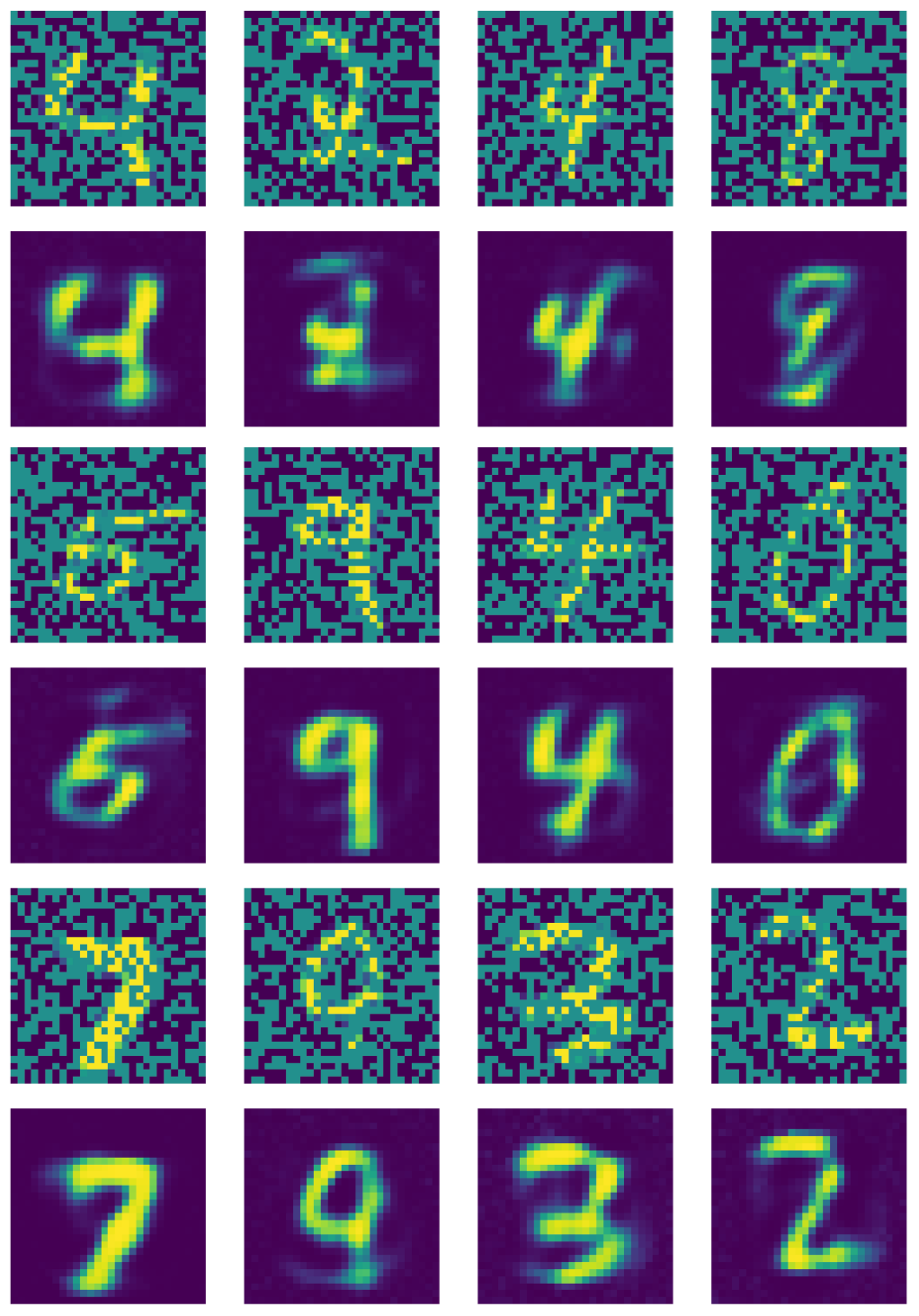
図21: デノイジングオートエンコーダーの出力

カーネルの比較

入力層の次元が $28 \times 28 = 784$ であるという事実にもかかわらず、次元が 500 の隠れ層は、画像中の黒いピクセルの数のせいで、まだオーバーコンプリートな隠れ層であることに注意することが重要です。 以下に、訓練されたアンダーコンプリートな標準的なオートエンコーダーで使用されたカーネルの例を示します。明らかに、数字が存在する領域のピクセルは何らかのパターンの検出を示しており、この領域外のピクセルは基本的にランダムです。これは、標準的なオートエンコーダーが、数字が存在する領域の外側のピクセルを気にしていないことを示しています。

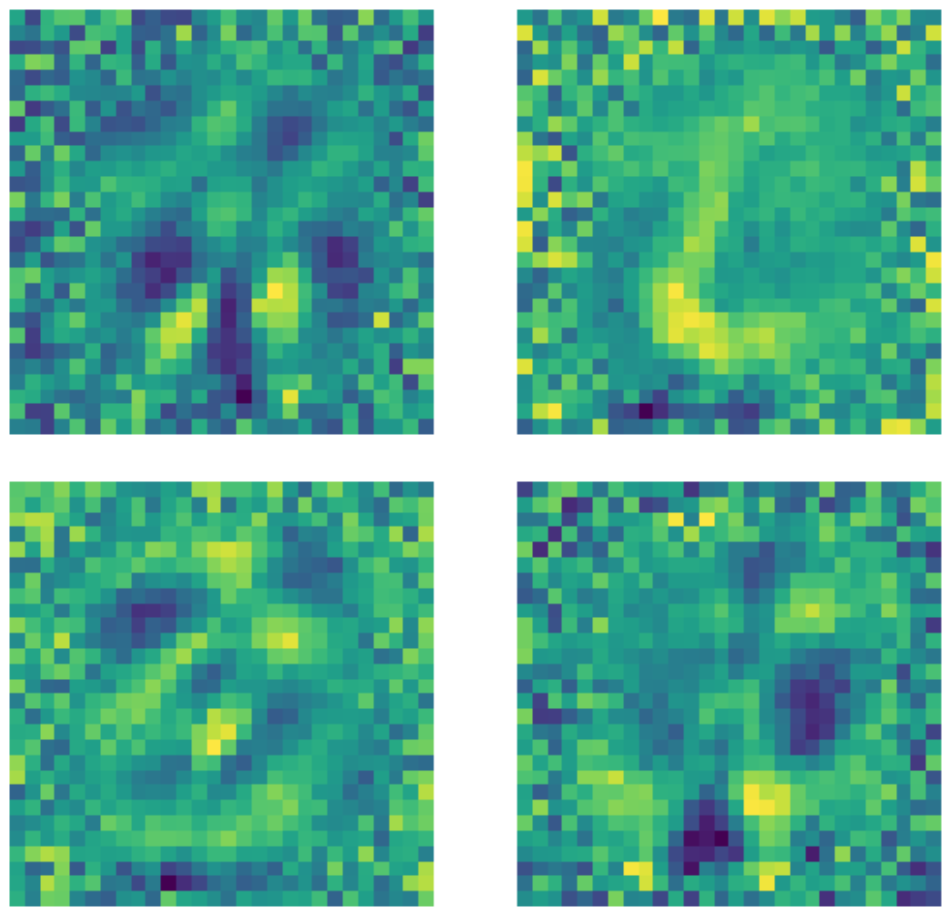
図22: 標準的な　AE のカーネル.

一方、同じデータを、モデルを学習する前に各画像にドロップアウトマスクが適用されるデノイジングオートエンコーダーに与えると、何か異なることが起こります。パターンを学習するすべてのカーネルは、数字が存在する領域の外側のピクセルをある一定の値に設定します。ドロップアウトマスクが画像に適用されるので、モデルは数字の領域の外側のピクセルを気にするようになりました。

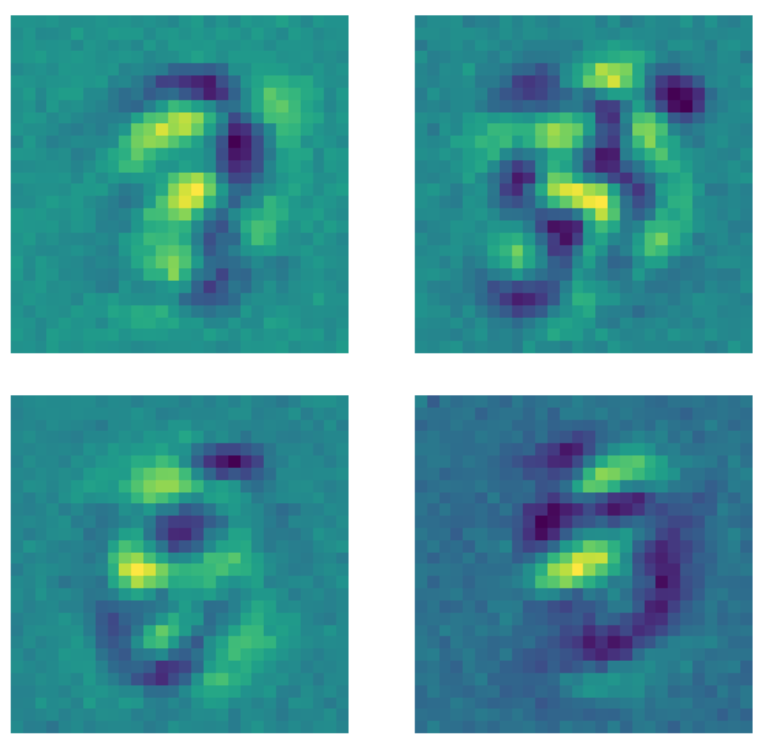
図23: デノイジングオートエンコーダーのカーネル

state-of-the-artの結果と比較しても、実際にこのオートエンコーダーの性能は優れています！結果は以下の通りです。

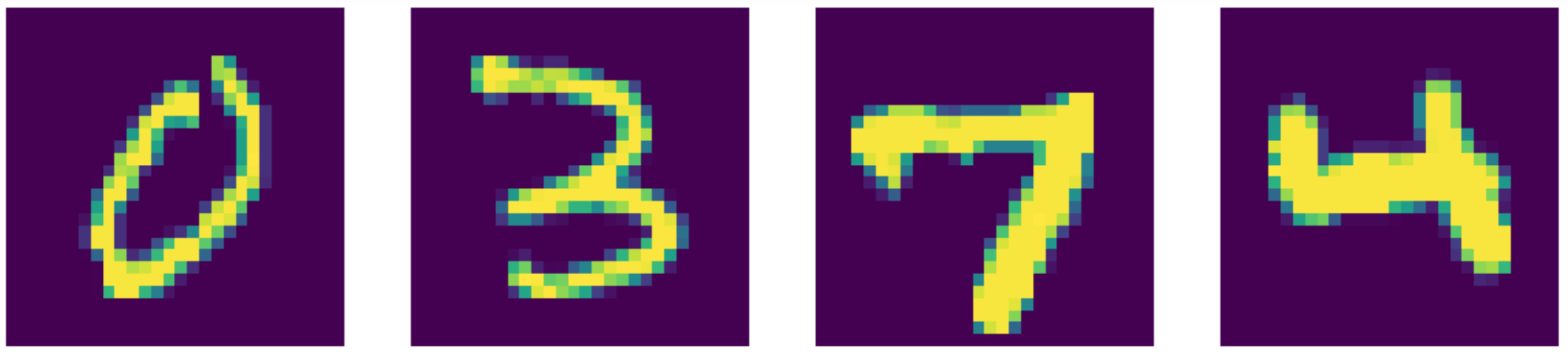
図24: 入力データ (MNIST)

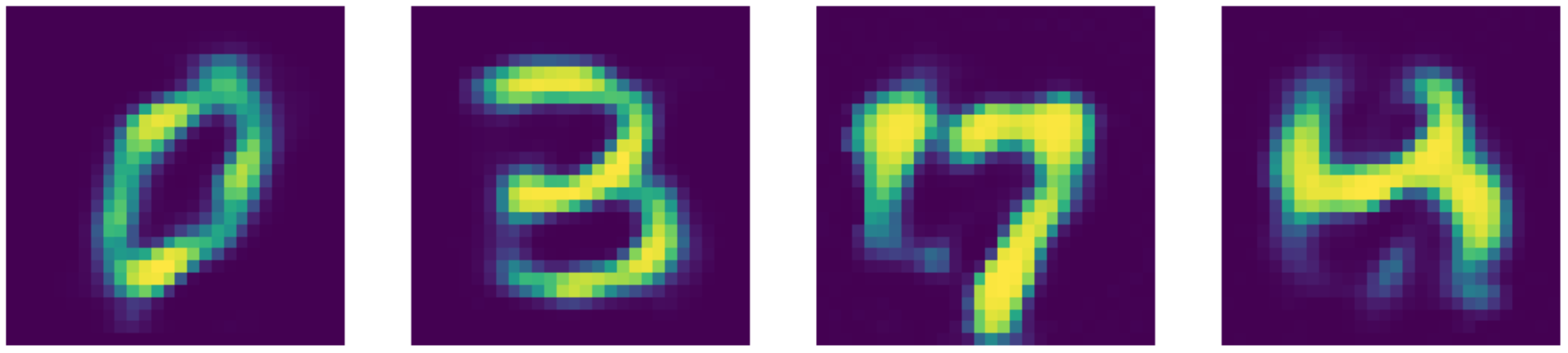
図25: デノイジングオートエンコーダーの再構成結果

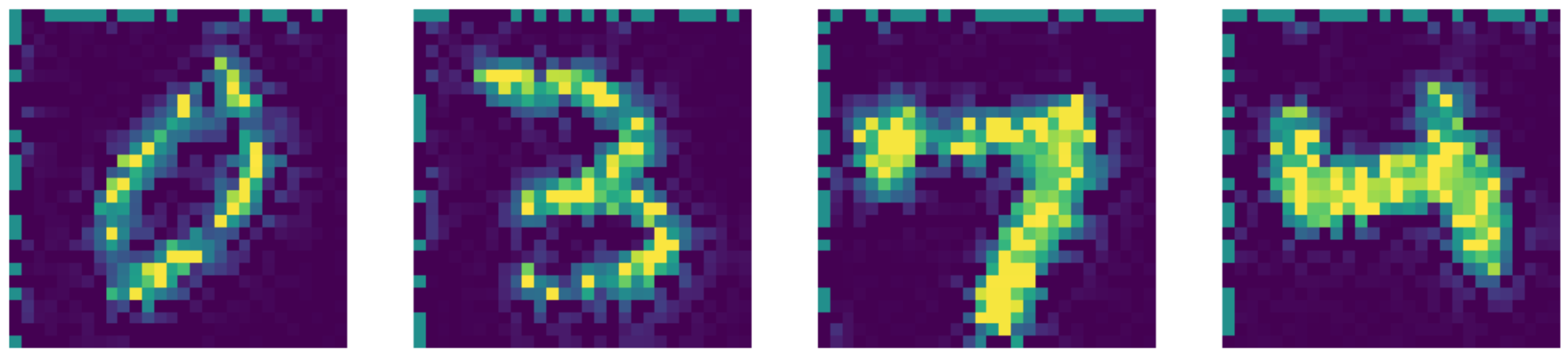
図26: Telea 2004によって提案されたアルゴリズムを用いた画像修復の結果

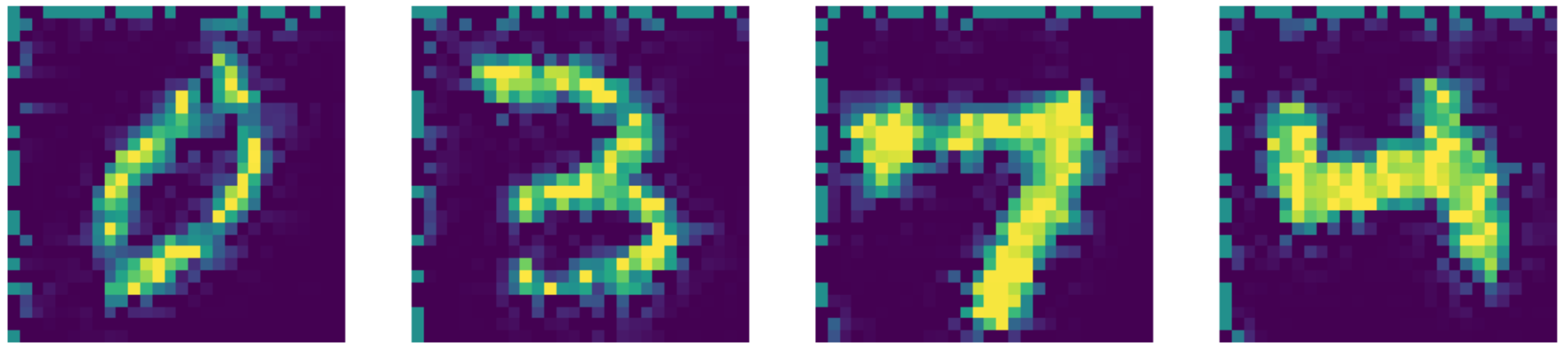
Figure 27: Bertalmio et al 2001によって提案されたNavier-Stokes方程式に基づくアルゴリズムを用いた画像修復の結果