SSL、EBMの詳細と例

自己教師あり学習

自己教師あり学習(SSL)は教師あり学習と教師なし学習の両方を含んでいます。SSLのpretextタスク（本来解きたいタスクの前に解く補助的なタスクのこと）の目的は、入力の良い表現を学習して、その後の教師ありタスクに使用できるようにすることです。SSLでは、データのある部分が与えられた時、モデルはその他の部分を予測するように訓練されます。例えば、BERTはSSLの技術を用いて訓練され、デノイジイングオートエンコーダー(DAE)は特に自然言語処理(NLP)において最先端の（state-of-the-artの、SOTAの）結果を示しています。

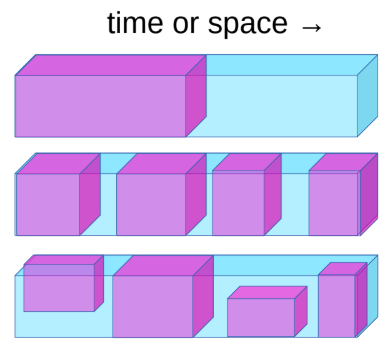
図1: 自己教師あり学習

自己教師あり学習タスクは、以下のように定義することができます。

• 過去から未来を予測する。
• 目に見えるものからマスクされたものを予測する。
• すべての利用可能な部分から任意の遮蔽された部分を予測する。

例えば、カメラが移動したときに次のフレームを予測するようにシステムが訓練されている場合、システムは暗黙のうちに奥行きと視差を学習します。これにより、システムは、視界から遮られた物体が消えるのではなく存在し続けることや、生身の物体、無生物、背景の区別を学習することを余儀なくされます。また、重力のような直観物理学を学習してしまうこともあります。

最先端のNLPシステム（BERT）は、SSLタスクで巨大なニューラルネットワークを事前に訓練します。文中の単語の一部を削除して、欠けている単語をシステムに予測させるのですが、これは非常にうまくいっています。同様のアイデアは、コンピュータビジョンの分野でも試されました。下の画像のように、画像を撮影して、画像の一部を削除して、欠落している部分を予測するモデルを訓練することができます。

図2: コンピュータビジョンにおける対応する結果

これらのモデルは足りていなかった部分を補うことはできますが、NLPシステムと同じレベルの成功を収めたとはいえません。これらのモデルによって生成された内部表現をコンピュータビジョンシステムに入力しても、ImageNet上で教師ありの方法で事前に訓練されたモデルに勝つことはできません。ここでの違いは、NLPが離散的であるのに対し、画像は連続的であるということです。成否を分けた点は、離散領域では不確実性の表現方法を知っているため、可能な出力に対して大きなソフトマックスを使うことができますが、連続領域ではそうではないという点です。

知的システム（AIエージェント）が知的な意思決定を行うためには、周囲や自分自身の行動の結果を予測する能力が必要です。世界は完全に決定論的というわけではなく、機械/人間の脳にはあらゆる可能性を説明するのに十分な計算能力があるわけではないので、不確実性の伴う高次元空間の中で予測することを、AIシステムに教える必要があります。そのためには、エネルギーベースモデル（EBM）が非常に有用です。

ビデオの次のフレームを予測するために最小二乗法を使用して訓練されたニューラルネットワークは、正確に未来を予測することができません。実際、損失を減らすために訓練データから次のフレームのすべての可能性を平均化することを学習するため、画像がぼやけてしまいます（ぼやけた画像を学習してしまいます）。

次のフレームの予測を行うための解決策としての潜在変数つきエネルギーベースモデル

線形回帰とは異なり、潜在変数つきエネルギーベースモデルは、世界について知っていることと、現実に起こったことについての情報を与えてくれる潜在変数とを、利用します。これら2つの情報を組み合わせて、実際に起こったことに近い予測を行うことができます。

これらのモデルは、システムのエネルギーを最小にする潜在変数を使った予測によって、入力$x$と実際の出力$y$の間の適合性を評価するシステムと考えることができます。入力$x$を観測し、入力$x$と潜在変数$z$の異なる組み合わせに対して可能な予測$\bar{y}$を生成し、システムの予測誤差であるエネルギーを最小化するものを選択するのです。

潜在変数に応じて、私たちはすべてのありうる予測に行き着くことができます。潜在変数は、入力 $x$ には存在しない出力 $y$ に関する重要な情報の一部と考えることができるのです。

スカラー値のエネルギー関数には2つのバージョンがあります。

1. 条件付き$F(x, y)$：$x$ と $y$ の間の適合度を測る。
2. 条件なし$F(y)$：$y$ の成分間の適合度を測る。

エネルギーベースモデルの学習

$F(x, y)$をパラメトライズするようにエネルギーベースモデルを訓練するための学習モデルには、2つのクラスがあります。

1. コントラスティブ法: $F(x[i], y[i])$を押し下げ、他の点 $F(x[i], y’)$を押し上げます。
2. アーキテクチャ法： 正則化によって低エネルギー領域の体積を制限するように、あるいは最小化するように$F(x, y)$を構築します。

エネルギー関数を構成するためには7つの戦略があります。コントラスティブ法は、押し上げるポイントの選び方によって異なる方法が存在します。一方でアーキテクチャ法は、コードの情報容量をどのように制限するかという点で異なる方法が存在します。

コントラスティブ法の例としては、最尤法による学習があります。エネルギーは正規化されていない負の対数密度と解釈できることを説明しました。このエネルギーを用いたギブス分布は、 $x$ が与えられたときの $y$ の尤度を与えてくれます。これは次のように定式化できます。

最尤法は、分子を大きく、分母を小さくして尤度を最大化しようとします。これは、以下の $L(Y, W) = -log(P(Y \mid W))$ を最小化することと等価です。

1つのサンプル$Y$に対する負の対数尤度損失の勾配は次のようになります。

上記の勾配におけるデータ点 $Y$ での勾配の第一項と、勾配の第二項は、すべての $Y$ に渡るエネルギーの勾配の期待値を与えてくれます。したがって、勾配降下法を実行するときには、最初の項はデータ点 $Y$ に与えられるエネルギーを減らそうとし、2番目の項は他のすべての $Y$ に与えられるエネルギーを増やそうとします。

エネルギー関数の勾配は一般的に非常に複雑であるため、この積分を推定したり、近似したりすることは、ほとんどの場合で難解であり、非常に興味深いケースです。

潜在変数つきエネルギーベースモデル

潜在変数モデルの主な利点は、潜在変数を通して複数の予測を可能にすることです。$z$ が集合上で変化するので、$y$ はありうる予測がなす多様体の上で変化します。いくつかの例があります。

1. K平均法
2. スパースモデリング
3. GLO

これらには2つのタイプがあります：

1. $y$が$x$に依存する条件付きモデル
   1. \[F(x,y) = \text{min}_{z} E(x,y,z)\]
   2. \[F_\beta(x,y) = -\frac{1}{\beta}\log\int_z e^{-\beta E(x,y,z)}\]
2. スカラー値のエネルギー関数 $F(y)$ を持つ条件なしモデル（これは$y$の成分間の適合度を測ります）
   1. \[F(y) = \text{min}_{z} E(y,z)\]
   2. \[F_\beta(y) = -\frac{1}{\beta}\log\int_z e^{-\beta E(y,z)}\]

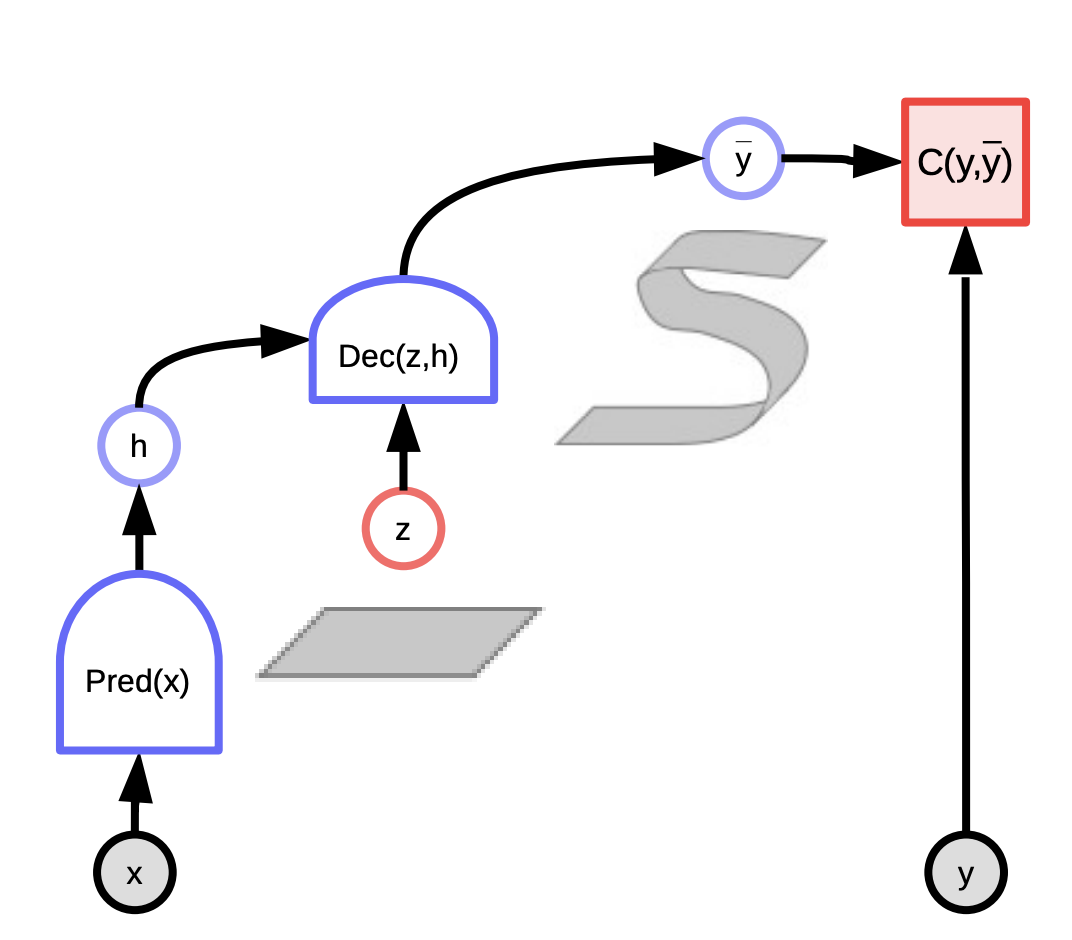
図3: 潜在変数つきEBM

潜在変数つきEBMの例: $K$平均法

K平均法は単純なクラスタリングアルゴリズムですが、$y$についての分布を考えることでエネルギーベースモデルとして考えることもできます。エネルギー関数は $E(y,z) = \Vert y-Wz \Vert^2$ で、ここでは$z$はone-hotベクトルです。

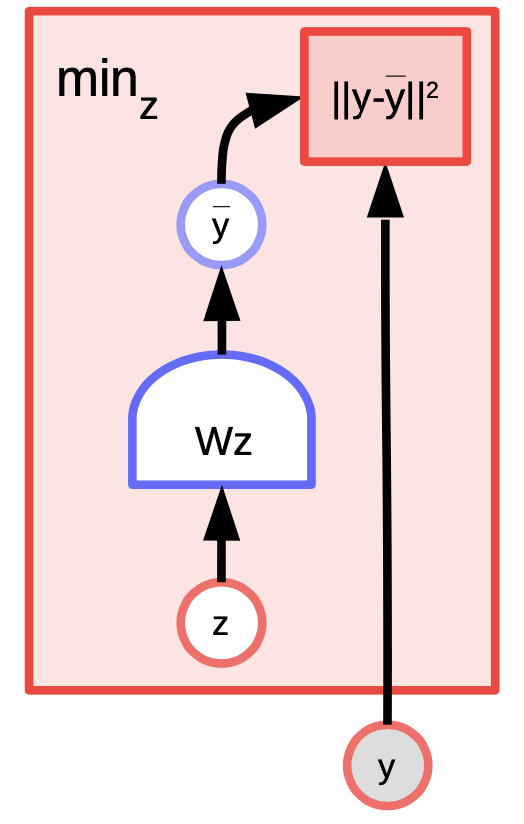
図4: K平均法の例

$y$ と $k$ の値が与えられると、 $k$ 個のありうる $W$ の列のうち、どの列が再構成誤差、またはエネルギー関数を最小化するかを求めることで推論を行うことができます。このアルゴリズムを訓練するには、 $y$ に最も近い $W$ の列を選択するように $z$ を求め、その後、勾配法を行ってさらに近づけようとし、その処理を繰り返すというアプローチを採用することができます。しかし、実際には座標降下法の方がうまくいくいきますし、学習も速くなります。

下のプロットでは、ピンクの螺旋に沿ったデータ点を見ることができます。この線を囲む黒い塊は、 $W$ の各プロトタイプの周りの二次元の井戸のようなものに対応しています。

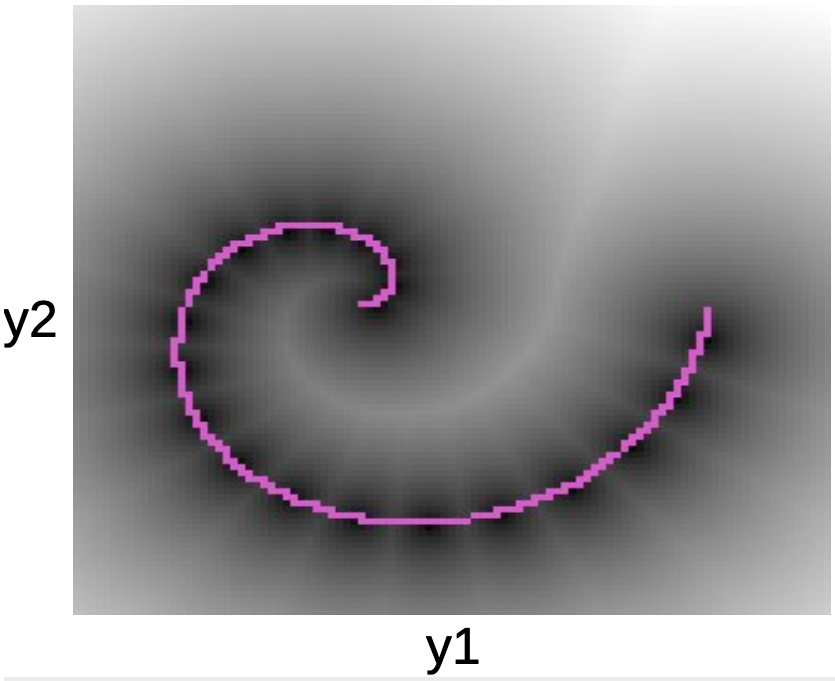
図5: 螺旋のプロット

エネルギー関数を学習すると、次のような問いに答えることができるようになります。

1. ある点 $y_1$ が与えられたとき、 $y_2$ を予測できるか？
2. $y$ が与えられたとき、データ多様体上で最も近い点を見つけることができるか？

K平均法は（コントラスティブ法とは対照的に）アーキテクチャ法に属します。したがって、エネルギーをどこかに押し上げるのではなく、特定の領域でエネルギーを押し下げるだけです。欠点としては、いったん $k$ の値が決まると、エネルギーが $0$ の $k$個の点しか存在しなくなり、それ以外の点はすべてエネルギーが高くなり、遠ざかるほどそのエネルギーが二次関数的に大きくなるという点あります。

コントラスティブ法

Yann LeCun博士によると、誰もがいつかはアーキテクチャ法を使うようになるでしょうが、現時点では、画像に対してはコントラスティブ法が有効だとのことです。エネルギー面の輪郭とデータ点とを示した下の図について考えます。エネルギー面はデータの多様体上で最も低いエネルギーであることが理想です。したがって、訓練データサンプルの周辺のエネルギー（すなわち、$F(x,y)$の値）を低くしたいのですが、これだけでは十分ではないかもしれません。そこで、本来ならエネルギーが高いはずなのにエネルギーが低くなっている領域にある$y$のエネルギーも上げることにします。

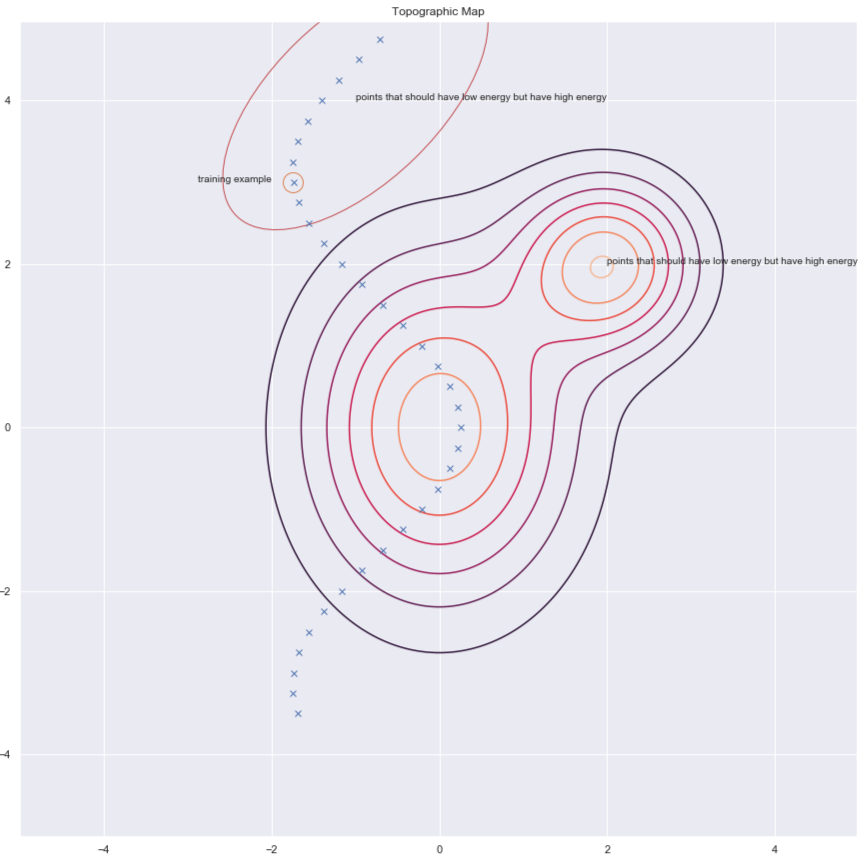
図6: コントラスティブ法

エネルギーを大きくしたい$y$の候補を見つける方法はいくつかあります。そのうちのいくつかの例として、

1. デノイジング・オートエンコーダー
2. コントラスティブダイバージェンス法
3. モンテカルロ法
4. マルコフ連鎖モンテカルロ法
5. ハミルトニアンモンテカルロ法

があります。

ここでは、デノイジング・オートエンコーダーとコントラストダイバージェンス法について簡単に説明します。

デノイジング・オートエンコーダー (DAE)

エネルギーを増やすために$y$を見つける方法の一つは、下のプロットの緑の矢印で示されているように、訓練データサンプルにランダムに摂動を加えることです。

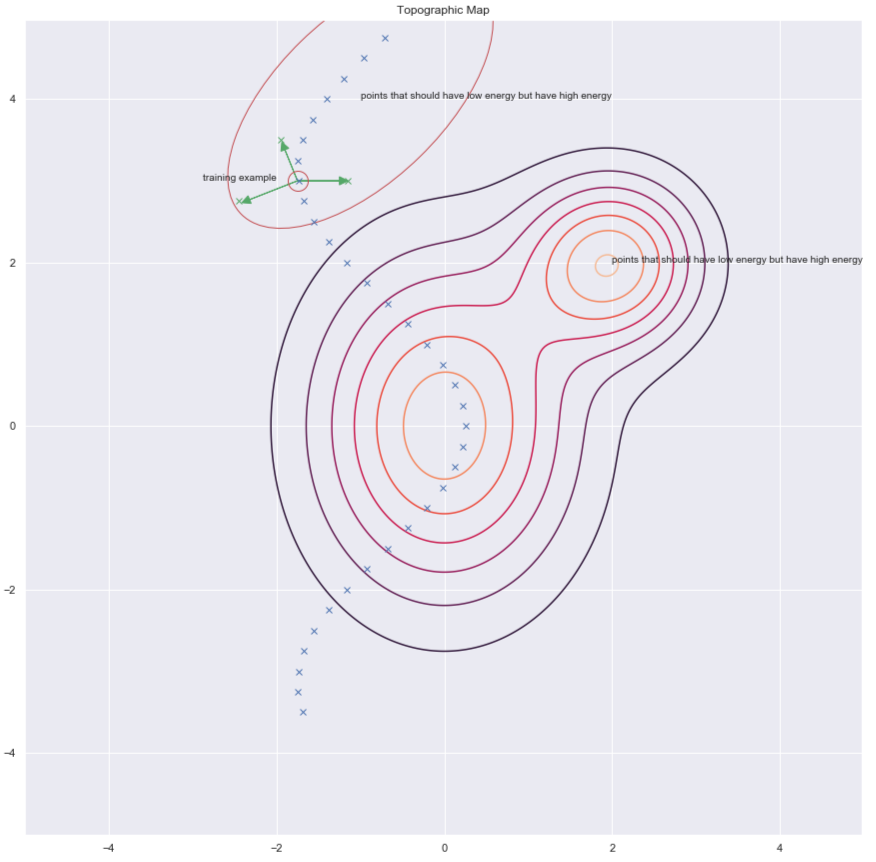
図7: 等エネルギー線図

破損したデータ点（摂動が加えられたデータ点）があれば、ここでエネルギーを押し上げることができます。すべてのデータ点についてこれを十分に何度も行うと、エネルギーサンプルは訓練データサンプルの周りで丸くなります。次のプロットは、訓練がどのように行われるかを示しています。

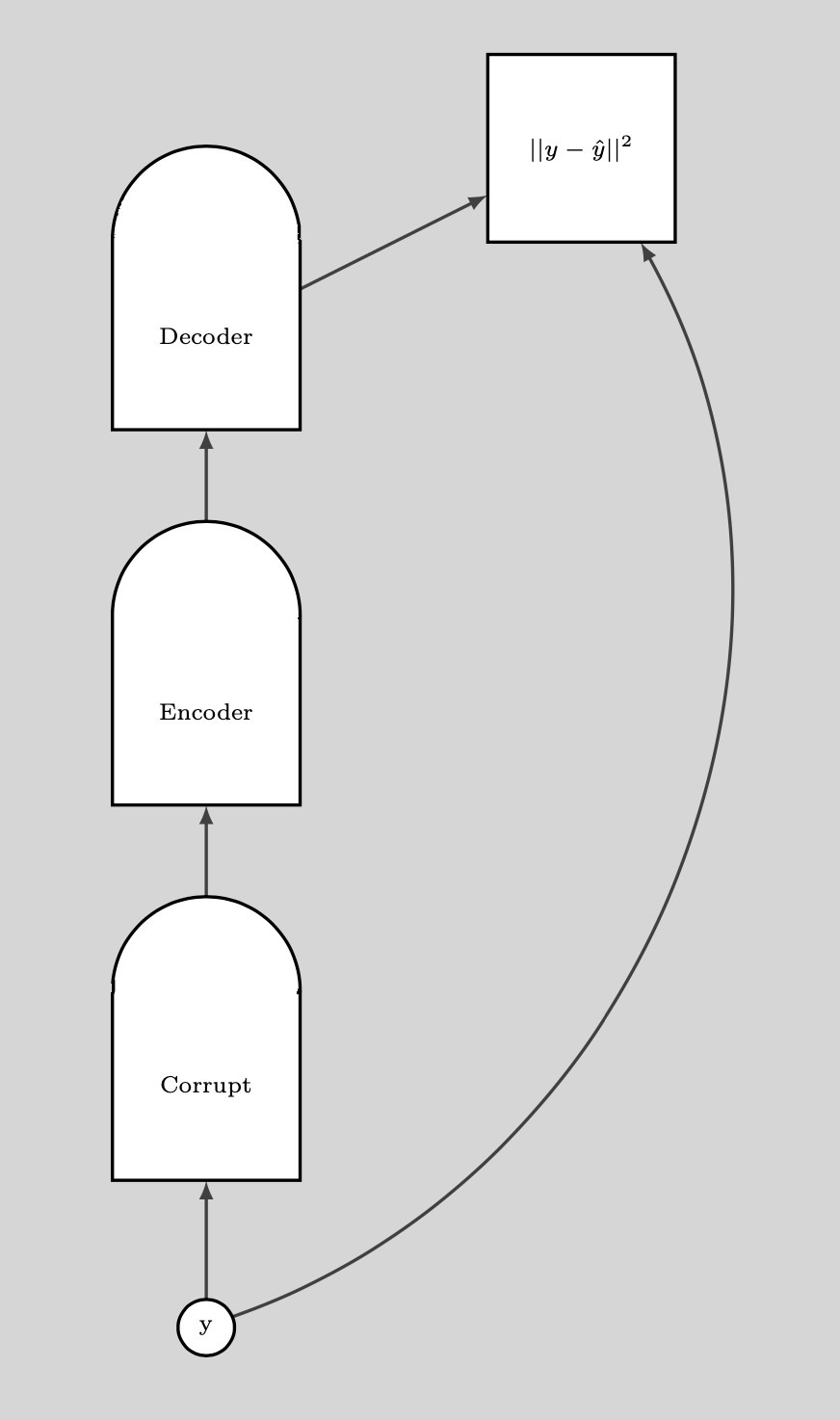
図8: 訓練

訓練のステップ

1. 点 $y$ を取って、それを破損させる
2. エンコーダとデコーダを訓練して、この破損したデータ点から元のデータ点を再構成します。

DAEが適切に訓練されている場合、データ多様性から遠ざかるにつれて、エネルギーは2次関数的に増加します。

次のプロットは、どのようにDAEを使うかを示しています。

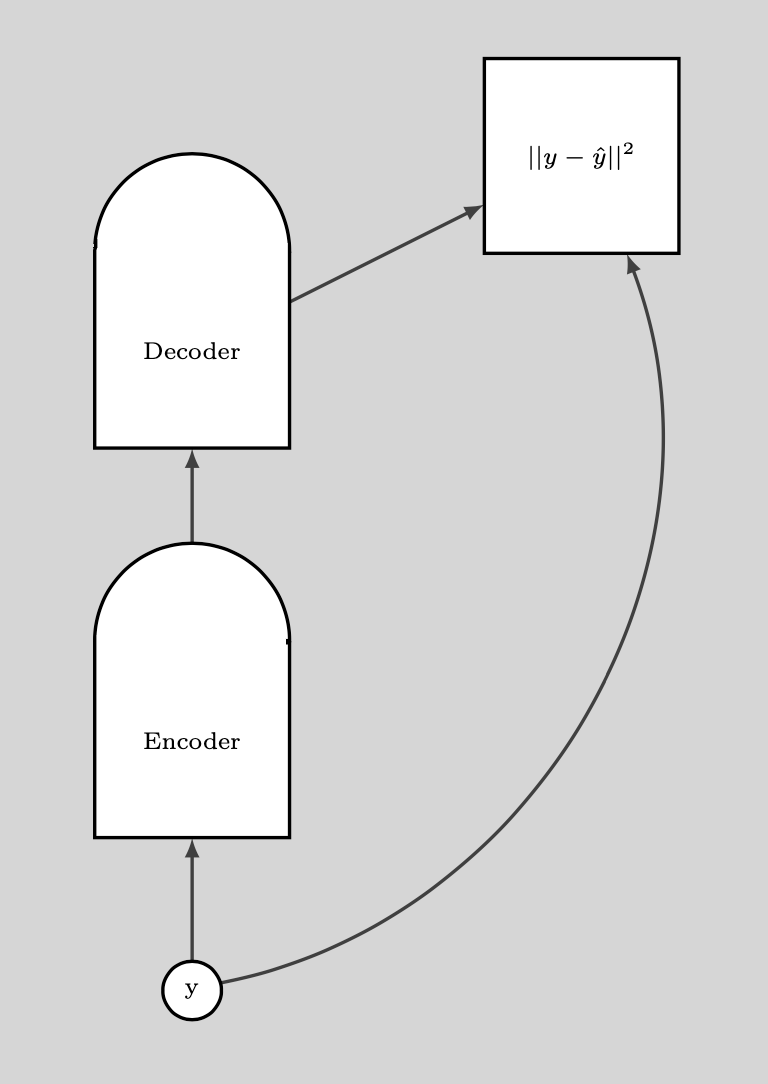
図9: どのように DAE を使うか

BERT

BERT は、テキストを扱っているので空間が離散的ですが、それを除けば同じように訓練されます。いくつかの単語をマスキングすることでデータを破損させ、これらの単語を予測しようとすることで再構成を行います。したがって、これはマスク付きオートエンコーダーとも呼ばれています。

コントラスティブ法

コントラスティブダイバージェンス法は、エネルギーを押し上げたい$y$の点を見つけるためのより賢い方法を提供してくれます。訓練点にランダムな摂動を与えて、勾配降下法を使ってエネルギー関数の上を下降させることができます。軌道の最後に、着地した点のエネルギーを押し上げます。これを緑の線で示したのが下のプロットです。

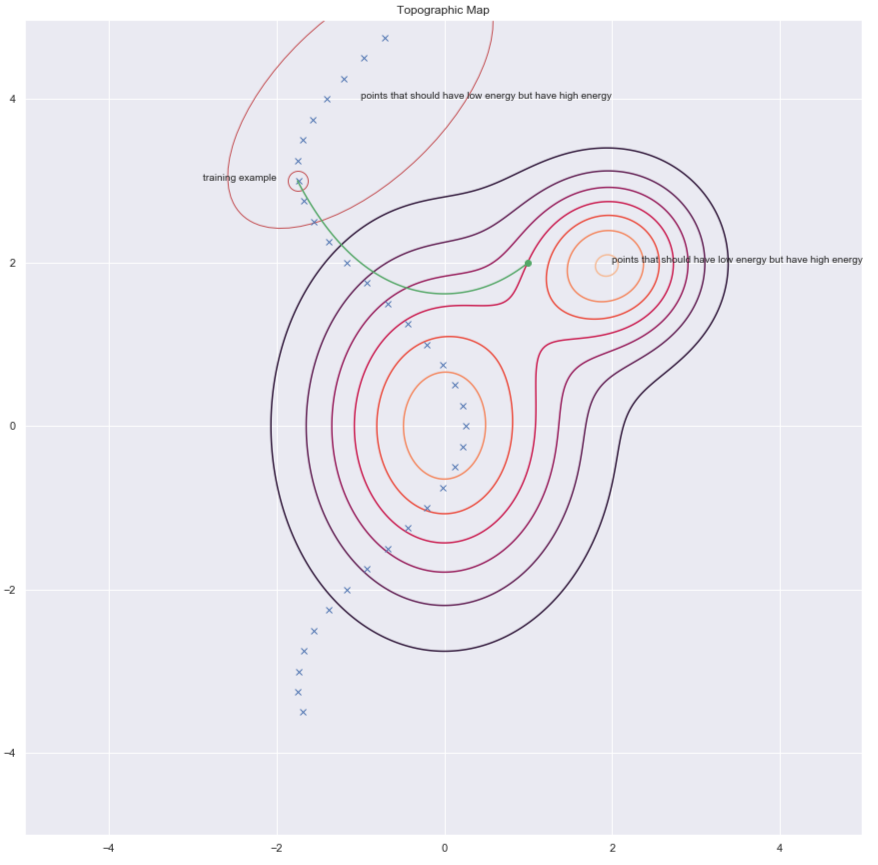
図10: コントラスティブダイバージェンス法