Architecture of RNN and LSTM Model

概要

RNNは、シーケンスデータを扱うために使用できるアーキテクチャの1つのタイプです。シーケンスとは何でしょうか？CNNのレッスンでは、信号はドメインによって1次元、2次元、3次元のいずれかになることを学びました。ドメインは、何から何にマッピングしているのか、によって定義されます。シーケンシャルデータを扱うのは、ドメインが時間軸なので、基本的には1次元データを扱うことになります。とはいえ、2つの方向がある2次元データを扱う場合もRNNを使うこともできます。

通常のニューラルネットワーク vs. リカレントニューラルネットワーク

図1は3層のバニラニューラルネットワークの図です。「バニラ」とは、アメリカの言葉で無地を意味します（つまりバニラニューラルネットワークは、通常のニューラルネットワークのことを指します）。ピンクの点が入力ベクトル$x$、中央の緑が隠れ層、最後の青の層が出力です。右のデジタル回路の例は、現在の出力が現在の入力にしか依存しない組合せ論理のようなものです。

図1: バニラアーキテクチャ

バニラニューラルネットワークとは異なり、リカレントニューラルネットワークでは、図2に示すように、電流出力は現在の入力だけでなく、システムの状態にも依存します。これは、デジタル回路の順序論理のようなもので、出力は「フリップフロップ」（デジタル回路の基本的な記憶装置）にも依存します。したがって、ここでの主な違いは、バニラニューラルネットワークの出力が現在の入力にのみ依存するのに対し、RNNの出力はシステムの状態にも依存するということです。

図2: RNNのアーキテクチャ

図3: 基本的なNNのアーキテクチャ

Yannの図は、あるテンソルと別のテンソル(あるベクトルから別のベクトル)との間のマッピングを表すために、ニューロン間にこれらの形状を追加します。例えば、図3では、入力ベクトルxは、この追加項目を介して隠れ表現hにマッピングされます。その後、別の変換を経て、隠れ層から最終的な出力に到達します。同様に、RNNの図では、ニューロン間で同じ追加項目を持つことができます。

図4: Yannの RNNのアーキテクチャ

４種類のRNNのアーキテクチャとその例

最初の例はベクトルからシーケンスへの変換です。入力は1つの点であり、緑色の点としてアノテーションされているのはシステムの内部状態の状態更新です。システムの状態が更新されると、各時間ステップで1つの特定の出力が発生します。

図5: Vec to Seq

このタイプのアーキテクチャの例としては、入力が１つの画像であり、出力が入力画像の英語の記述を表す単語のシーケンスとなるようなものが挙げられます。図6を用いて説明すると、ここでは、青い点それぞれが英単語の辞書のインデックスとなっています。例えば、出力が「This is a yellow school bus」という文であるとしましょう。まず、「This」という単語のインデックスを取得し、次に 「is」という単語のインデックスを取得します。このネットワークの結果の一部を以下に示します。例えば、1列目の最後の画像に関する記述は、「A herd of elephants walking across a dry grass field.」となっており、非常に洗練されています。そして2番目の列では、最初の画像は 「Two dogs play in the grass.」と出力されていますが、実際には3匹の犬です。最後の列は、「A yellow school bus parked in a parking lot.」のように、より間違った例です。一般的に、これらの結果は、このネットワークがかなり大幅に失敗することもあれば、うまくいくこともあることを示しています。これは、画像の表現である1つの入力ベクトルから、例えば英語の文章を構成する文字や単語である記号の列へと変化する場合です。このようなアーキテクチャを自己回帰型のネットワークと呼びます。自己回帰型のネットワークとは、前の出力を入力として与えられた下で、出力をするネットワークのことです。

図6: vec2seqの例: 画像から文章へ

2番目のタイプは、シーケンスから最終的にベクトルを返すものです。このネットワークはシンボルのシーケンスを与え続け、最後にのみ最終的な出力を与えます。これの応用として、Pythonを解釈するためにネットワークを使用することができます。例えば、入力はPythonプログラムの以下の行です。

図 7: Seq to Vec

図 8: Pythonコードの入力列

そうすると、ネットワークはこのプログラムの正解を出力することができるようになります。もう一つ、このようなもっと複雑なプログラムがあります。

図9: より複雑な場合のPython Codesの入力列

すると、出力は12184になるはずです。これら2つの例は、この種の操作を行うためにニューラルネットワークを訓練できることを示しています。記号のシーケンスを与えて、最終的な出力が特定の値になるように強制するだけです。

3つ目は、図10に示すように、シーケンスからベクトルへ変換し、そこからまたシーケンスへ変換を行うものです。このアーキテクチャは、かつて言語翻訳を実行するための標準的な方法でした。ここでは、ピンク色で示されている一連のシンボルから始まります。そして、すべてのものがこの最終的な$h$に凝縮されます。これは概念を表しているといえます。例えば、入力として文章を持っていて、それを一時的にベクトルに圧縮することができます。そして、どのような表現であれこの意味を獲得した後、ネットワークはそれを別の言語に展開します。例えば、英語の単語列の中の「Today I’m very happy」は、イタリア語や中国語に翻訳することができます。一般的に、ネットワークは入力として何らかのエンコーディングを取得し、それを圧縮表現に変換します。最後に、この圧縮された表現を与えられた下でデコーディングを行います。最近では、次の講義で紹介するTransformerのようなネットワークが、言語翻訳のタスクでこの方法を上回るパフォーマンスを発揮しています。このタイプのアーキテクチャは、約2年前(2018年)に最先端として使われていました。

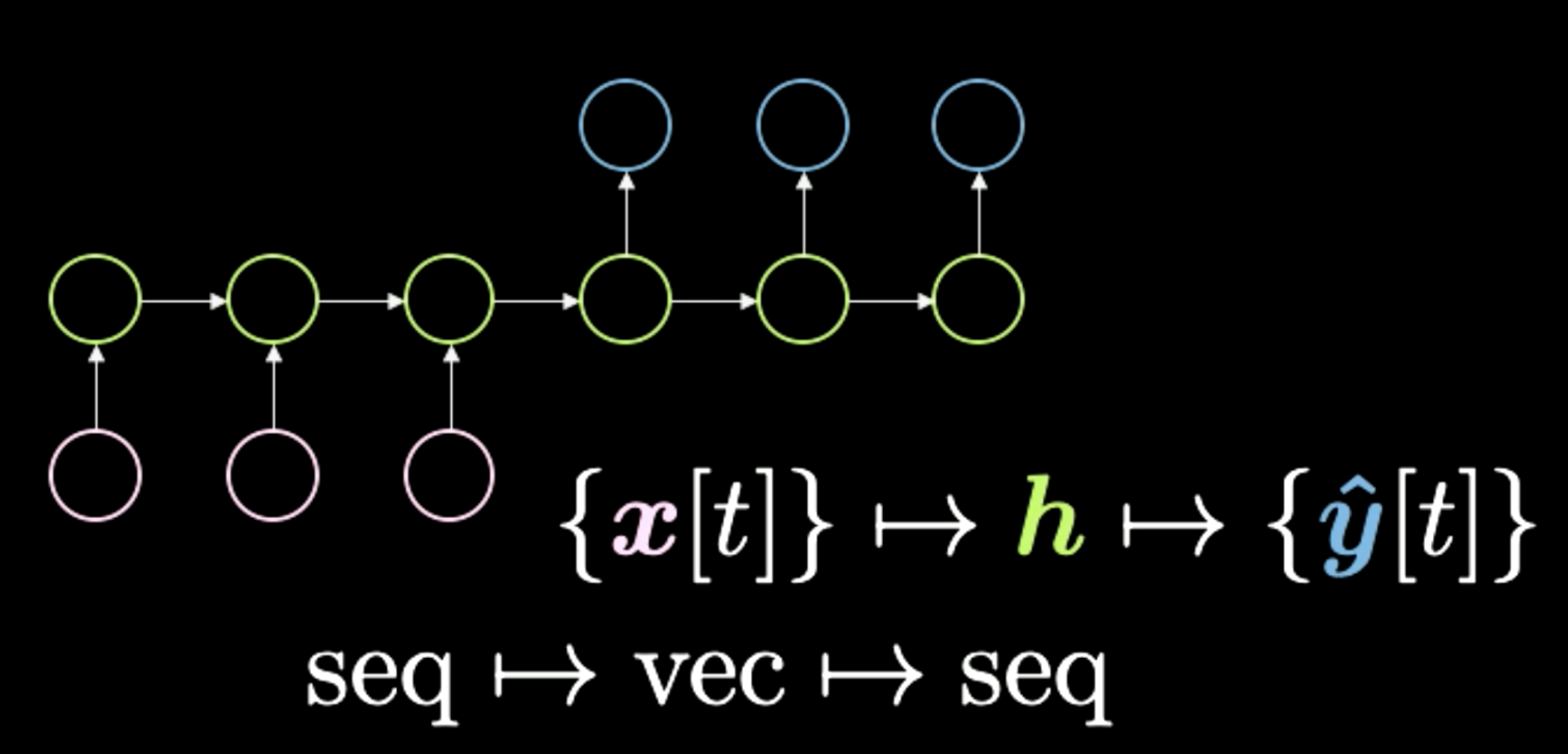
図10: Seq to Vec to Seq

潜在空間に対してPCAを行うと、このグラフのように意味でグループわけされた単語が得られます。

図11: PCAの後に意味でグループわけされた単語

詳しく見てみると、同じ場所に1月と11月のようにすべての月があることがわかります。

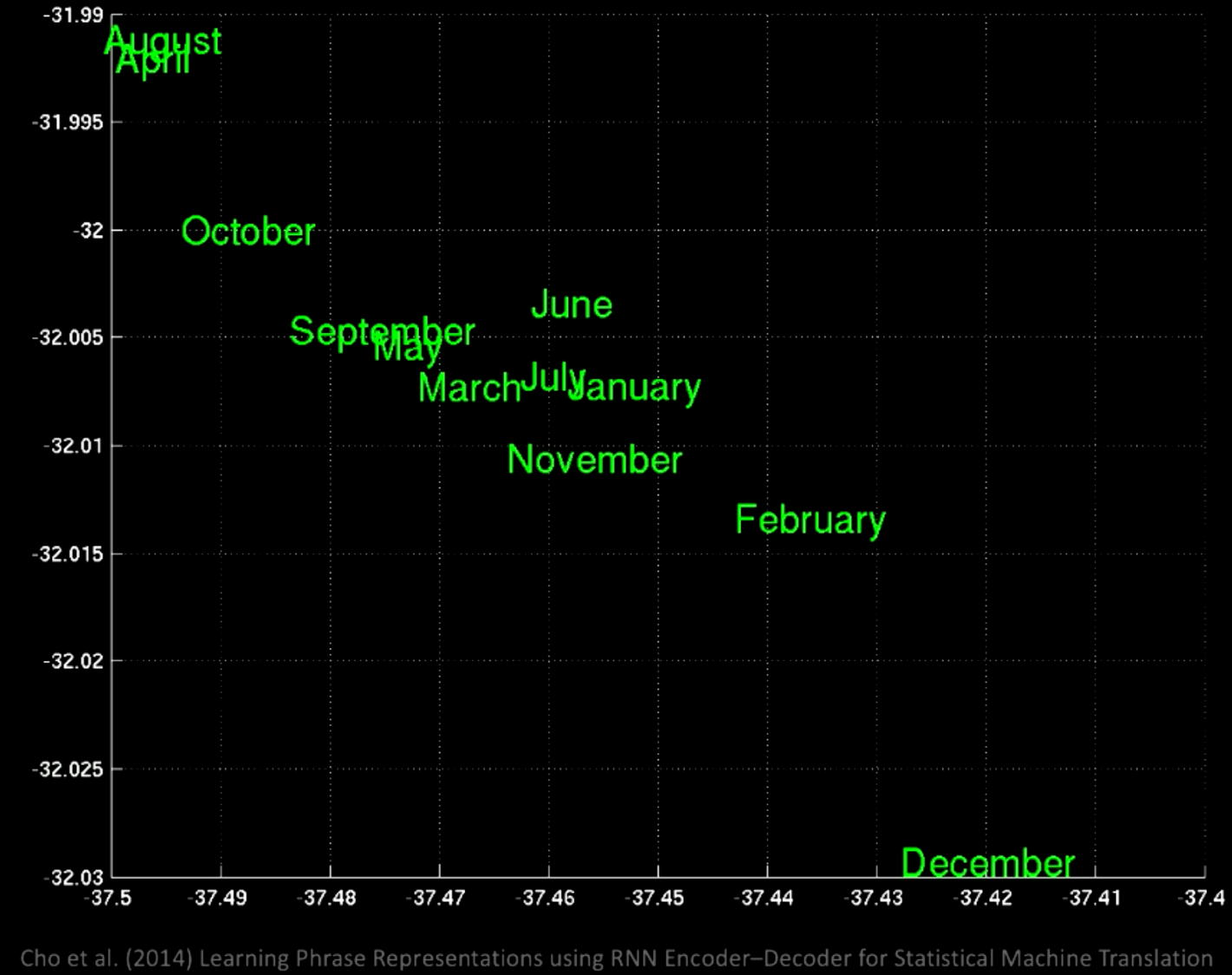
図12: 単語グループを拡大する

別の場所に焦点を当てると、「数日前」「数ヶ月後」などのフレーズが出てきます。

図13: 他の場所の単語のグループ

これらの例から、異なる場所が特定の共通の意味を持っていることがわかります。

図14は、この種のネットワークを学習することで、どのように意味論的な特徴を拾っていくかを示しています。この例では、男性と女性を結ぶベクトルと、王様と王妃を結ぶベクトルがあることがわかります。この埋め込み空間では、男性と女性のようなケースに適用しても、同じ距離が得られます。もう一つの例は、「歩いている」が「歩いた」になり、「泳いでいる」が「泳いだ」になります。常にこの種の特定の線形変換を、ある単語から別の単語へ、または国から首都へ行うことができます。

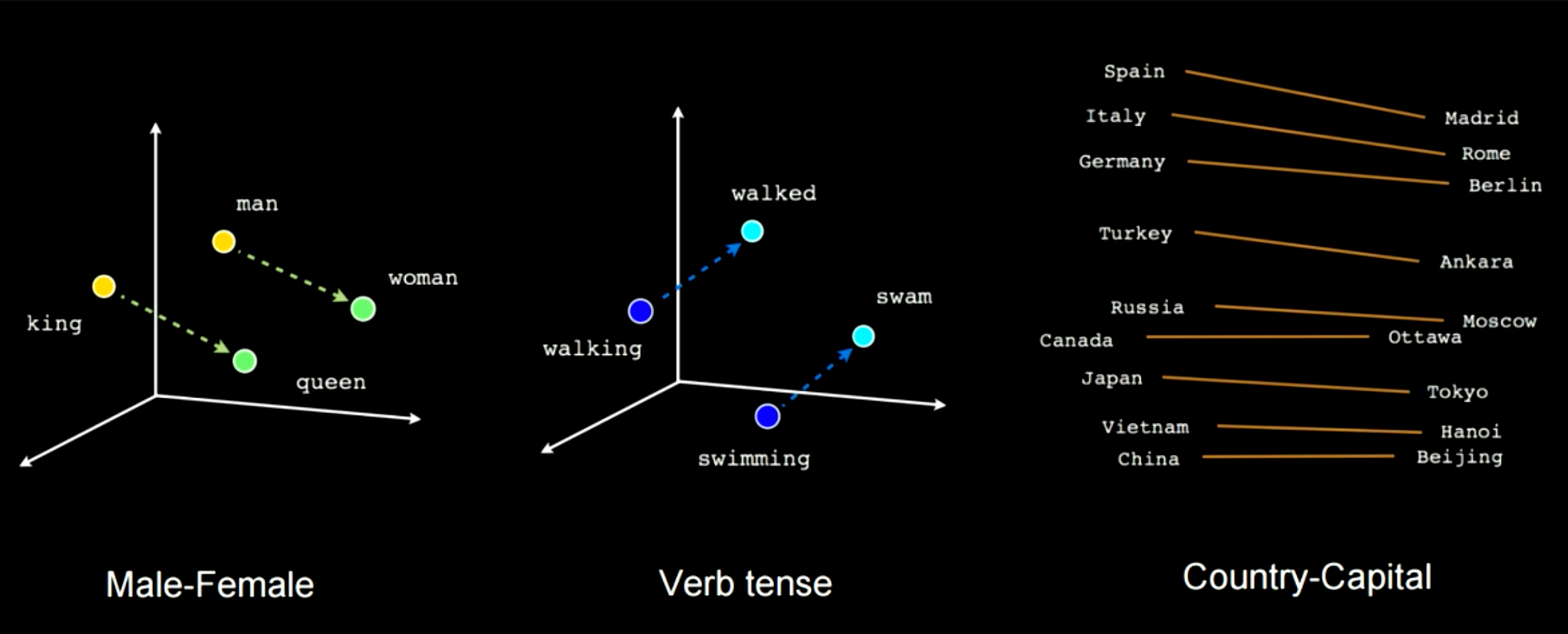
図4: 学習中に選ばれた意味的な特徴表現

最後となる4番目のケースは、シーケンスからシーケンスへの変換です。このネットワークでは、入力を受け取ると、出力を生成し始めます。このタイプのアーキテクチャの例としては、T9が挙げられます。他の例としては、キャプションへの音声変換があります。良い例としては、このRNN-writerがあります。「the rings of Saturn glittered while」と入力し始めると、次のような「two men looked at each other」を提案してくれます。このネットワークはいくつかのSF小説で訓練されたもので、何かを入力するだけで、本を書くのに役立つ提案をしてくれるようになっています。もう一つの例を図16に示します。一番上のプロンプトを入力すると、このネットワークは残りの部分を完成させようとします。

図5: Seq to Seq

図16: Seq to Seq による文書入力自動補完モデル

Back Propagation through time

モデルアーキテクチャ

RNNを学習するためには、backpropagation through time(BPTT)を用いる必要があります。RNNのモデルアーキテクチャを下図に示します。左の図はループ表現を用いたもので、右の図はループを時間の経過とともに1行に展開したものです。

図17: Back Propagation through time

隠れ表現は次のように表現されます

最初の式は、スタックされた入力の回転に非線形関数を適用したもので、隠れ層の前の設定が付加されています。式を簡単にするために、$W_h$は、$\left[ W_{hx}\ W_{hh}\right]$の2つの行列として書くことができるので、以下のように書くことができます。

これは入力のスタックされた表現に一致します。

$y[t]$は最終的な回転操作のところで計算され、その後、連鎖律を使用して、誤差を前回の時間ステップに逆伝播することができます。

言語モデリングをバッチ化する

記号のシーケンスを扱う場合、テキストを異なるサイズにバッチ化して処理することができます。例えば、次の図のようなシーケンスを扱う場合、時間領域が垂直方向に保存されているところでは、最初の部分をバッチ化することができます。この場合、バッチサイズは4に設定されます。

図18: バッチ化

BPTT期間$T$を3とすると、RNNの最初の入力$x[1:T]$と出力$y[1:T]$は次のように決定されます。

最初のバッチでRNNを用いる場合、まず、$x[1] = [a\ g\ m\ s]$をRNNに与え、$y[1] = [b\ h\ n\ t]$となるように出力を強制します。隠れ表現$h[1]$を次の時間ステップに送り、RNNが$x[2]$から$y[2]$を予測するのを助けます。$x[T]$と$y[T]$の最終集合に$h[T-1]$を送り込んだ後、$h[T]$と$h[0]$の両方の勾配を伝搬する処理をカットして、勾配が無限に伝搬しないようにします(.detach() in Pytorch)。全体の処理を下図に示します。

図19: バッチ化

勾配消失と勾配爆発

問題

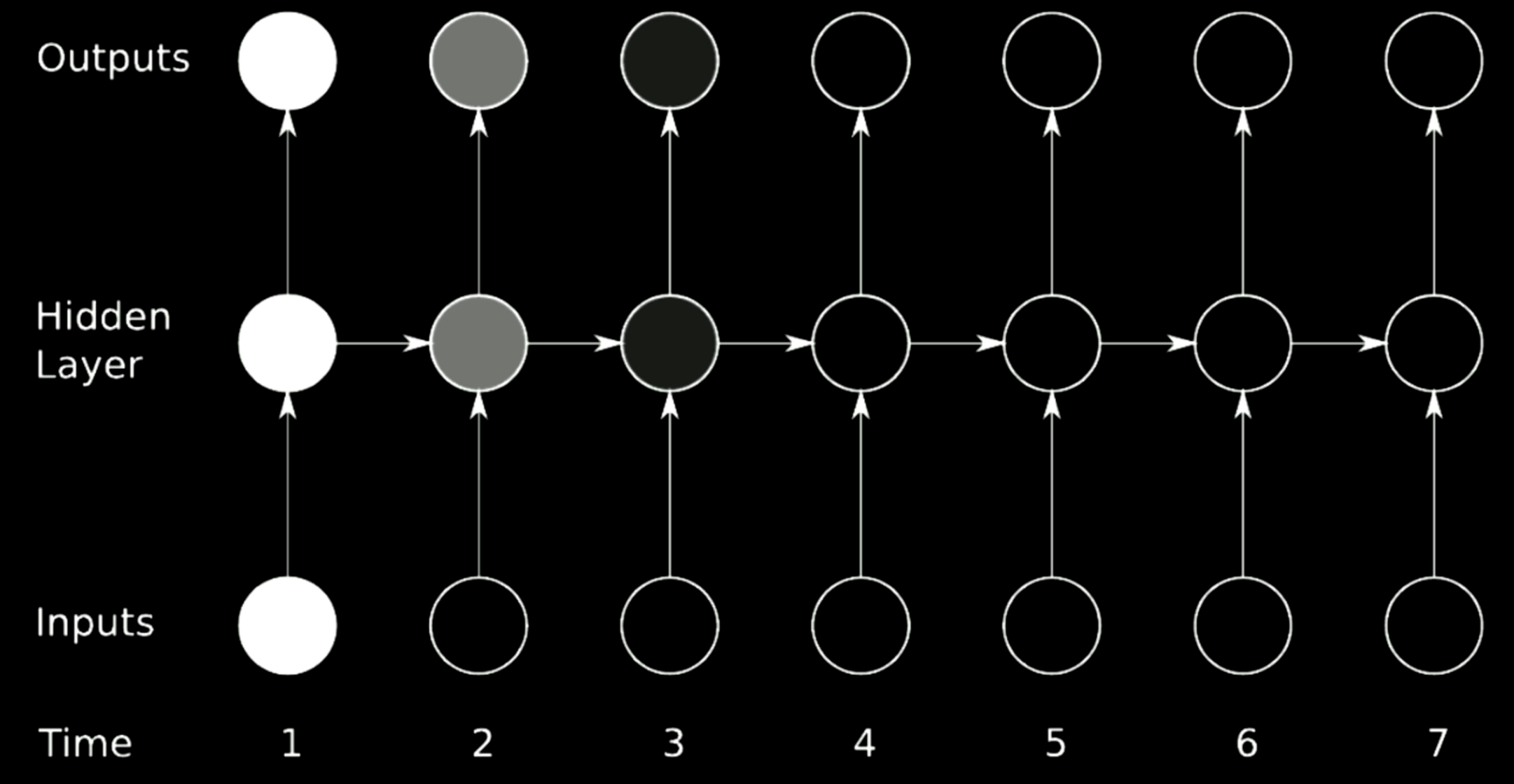
図20: 勾配消失

上の図は典型的なRNNのアーキテクチャです。RNNで前のステップの回転を行うために、上のモデルでは横向きの矢印と見なすことができる行列を使っています。行列は出力の大きさを変えることができるので、選択する行列式が1よりも大きいと、時間の経過とともに勾配が膨らみ、勾配爆発を起こしてしまいます。対照的に、選択する固有値が0を挟んで小さい場合には、伝播過程は勾配を収縮させ、勾配消失につながります。

典型的なRNNでは、勾配はすべての可能な経路を通って伝搬されることで、勾配が消失または爆発する可能性を増加させます。例えば、時刻1の勾配は大きく、明るい色で示されています。それが1回転すると、勾配は大きく縮小し、時刻3では消滅してしまいます。

解

勾配爆発や消失を防ぐための理想的な方法は、接続をスキップすることです。これを実現するために、乗算ネットワークを使用することができます。

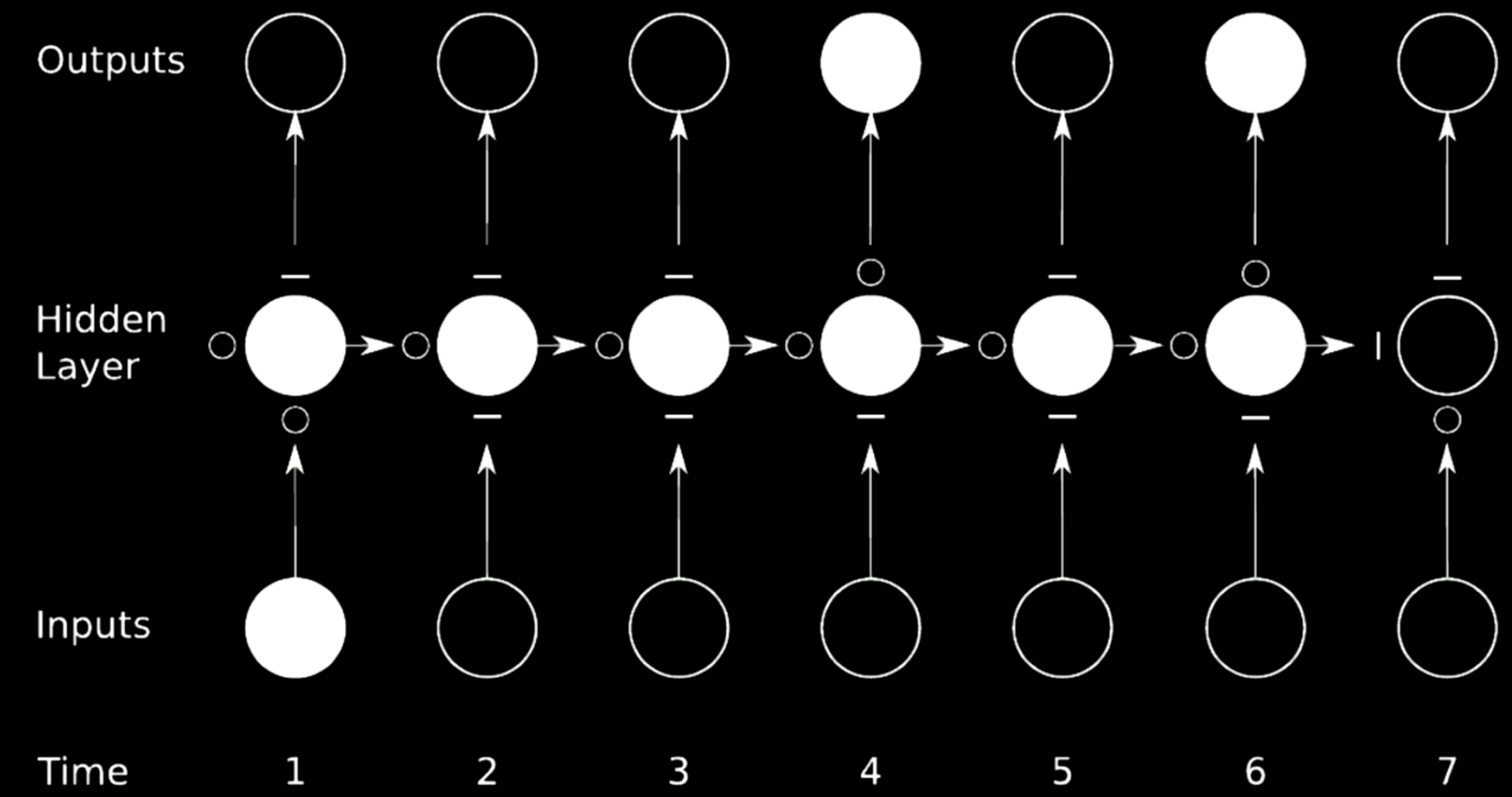
図21: スキップ接続

上記の場合、元のネットワークを4つのネットワークに分割します。最初のネットワークを例に考えてみましょう。このネットワークは、時刻１に入力から値を取り込んで、その出力を隠れ層の最初の中間状態に送ります。この状態には、他に3つのネットワークがあります。ここでは、$-$が伝搬を阻止し、$\circ$が勾配を通過させます。このような手法をゲート付きリカレントネットワークと呼びます。

LSTMはゲート付きリカレントネットワークの一つですが、以下の節で詳しく紹介します。

Long Short-Term Memory

モデルアーキテクチャ

以下はLSTMを表す式です。入力ゲートは黄色のボックスで強調されていますが、これはアフィン変換になります。この入力変換は $c[t]$ を乗算したもので、これが候補ゲートとなります。

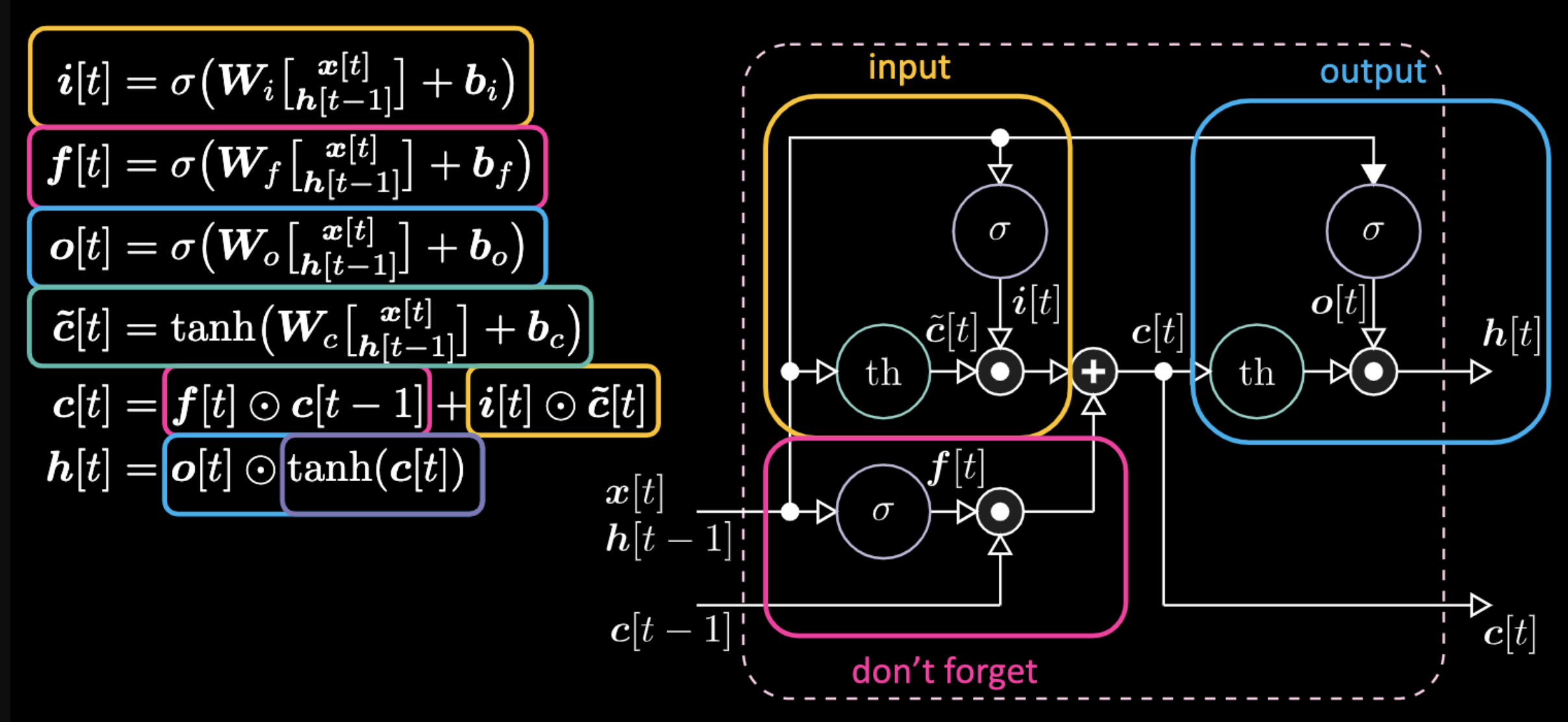
図22: LSTMのアーキテクチャ

忘却ゲートは、セルメモリの前の値$c[t-1]$に乗算されます。セルの合計値 $c[t]$ は、忘却ゲート + 入力ゲートです。最終的な隠れ表現は、出力ゲート$o[t]$とセルのtanhである$c[t]$との間の要素毎の掛け算です。最後に、候補ゲート $\tilde{c}[t]$ は、単純にリカレントネットです。つまり、出力を変調するための $o[t]$、忘れないようにするための $f[t]$、入力ゲートを変調するための $i[t]$があります。これらのメモリとゲートの間の相互作用は、すべて乗算的な相互作用です。$i[t]$, $f[t]$, $o[t]$は、すべてシグモイドですので、0から1の範囲におさまります。したがって、ゼロをかけると、閉じたゲートになりますし、1をかけると開いたゲートになります。

出力をオフにするにはどうすれば良いでしょうか？紫色の内部表現 $th$ を持ち、出力ゲートにゼロを入れたとします。そうすると、出力は何かかけるゼロになります。出力ゲートに1を入れると、紫色の内部表現と同じ値が得られます。

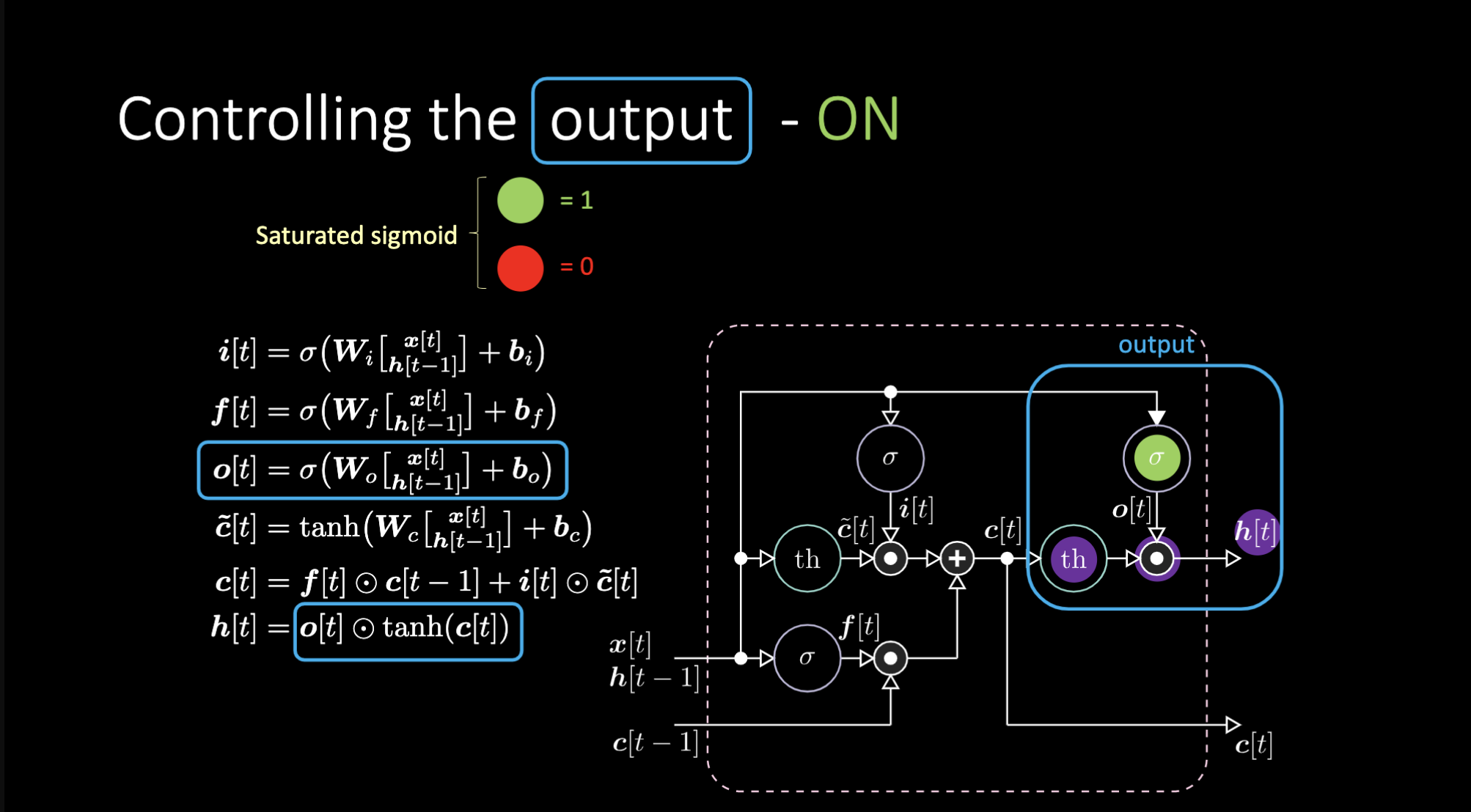
図23: LSTMのアーキテクチャ - 出力オン

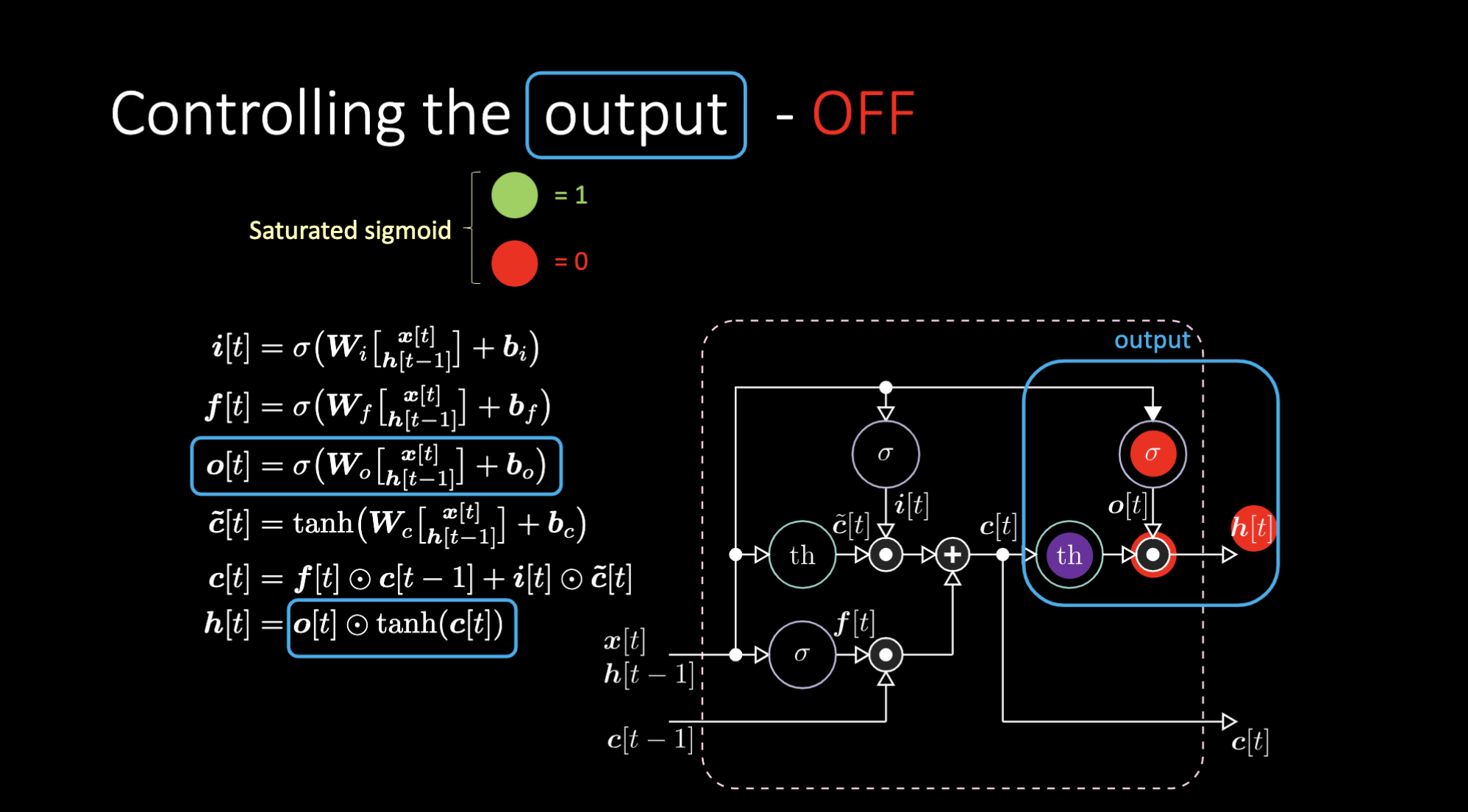
図24: LSTMのアーキテクチャ - 出力オフ

同様に、メモリを制御することもできます。例えば、$f[t]$と$i[t]$をゼロにすることで、メモリをリセットすることができます。乗算と和の後、メモリの中にゼロが入ります。そうでなければ、内部表現 $th$ をゼロにしたまま、$f[t]$ の中に 1 を入れておくことで、メモリを保持することができます。したがって、和は $c[t-1]$ を得て、それを送り出し続けます。最後に、入力ゲートで1を取得し、乗算が紫色になり、忘却ゲートで0を設定して、実際に忘れてしまうように書くことができます。

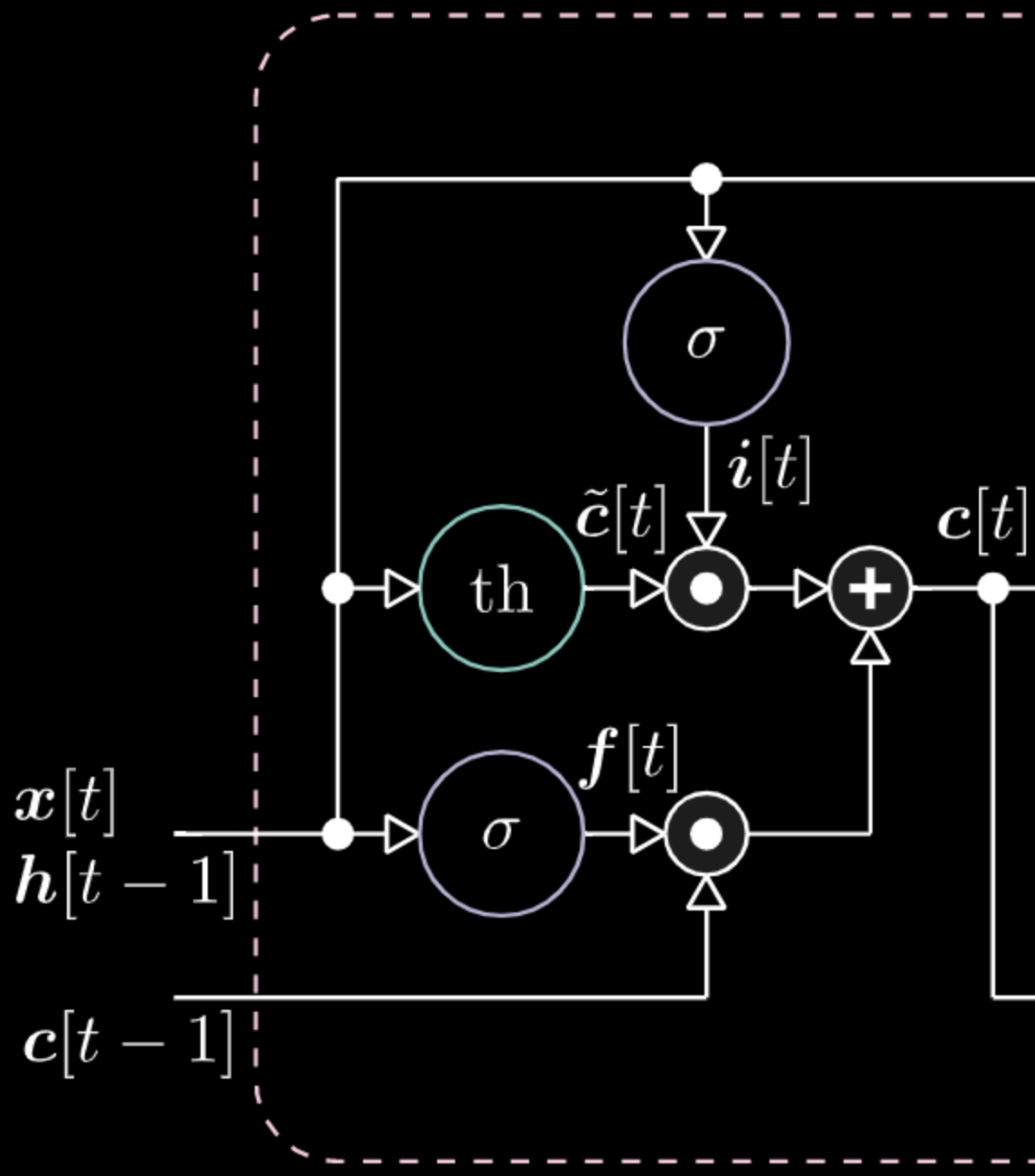
図25: メモリセルの可視化

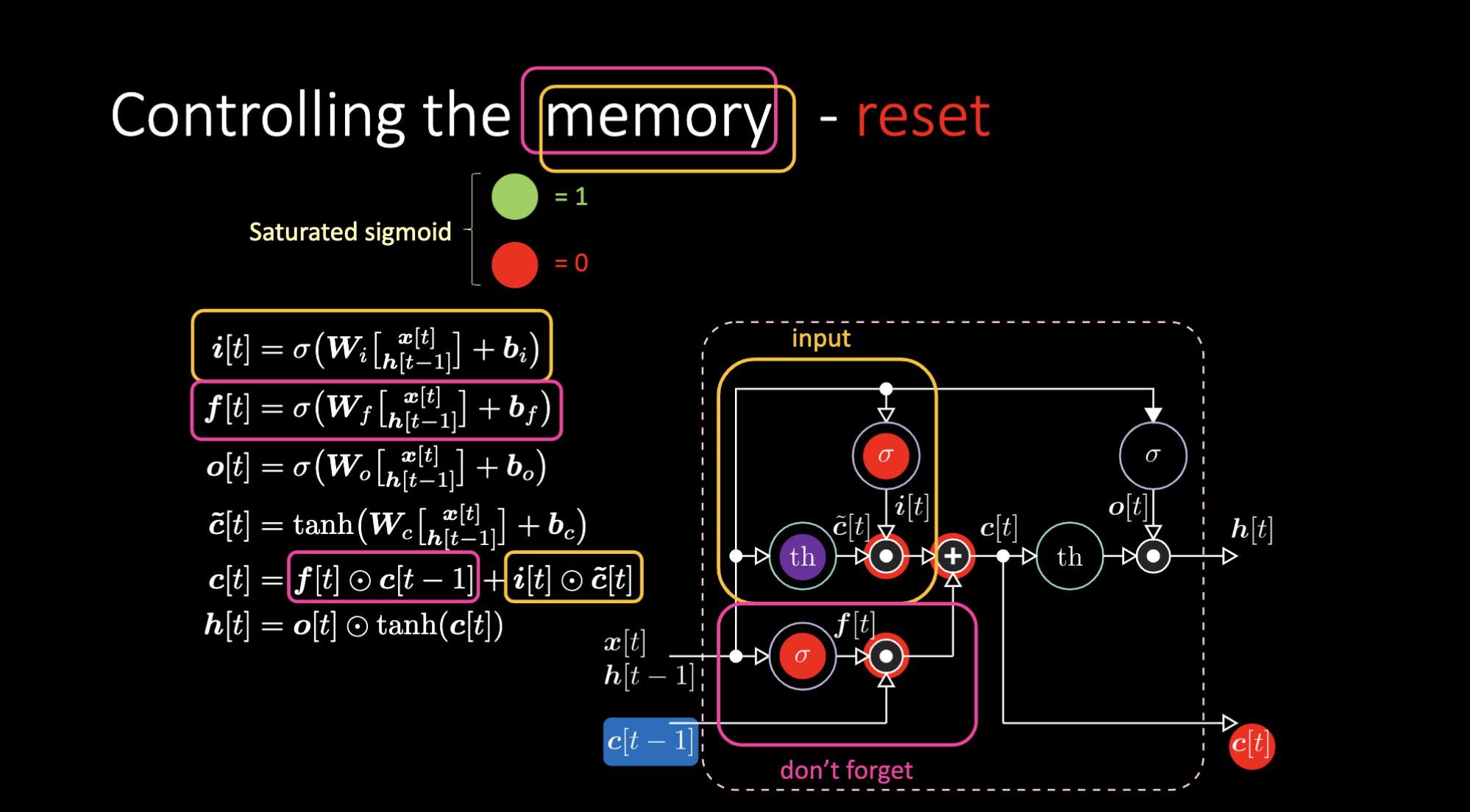
図26: LSTMのアーキテクチャ - メモリのリセット

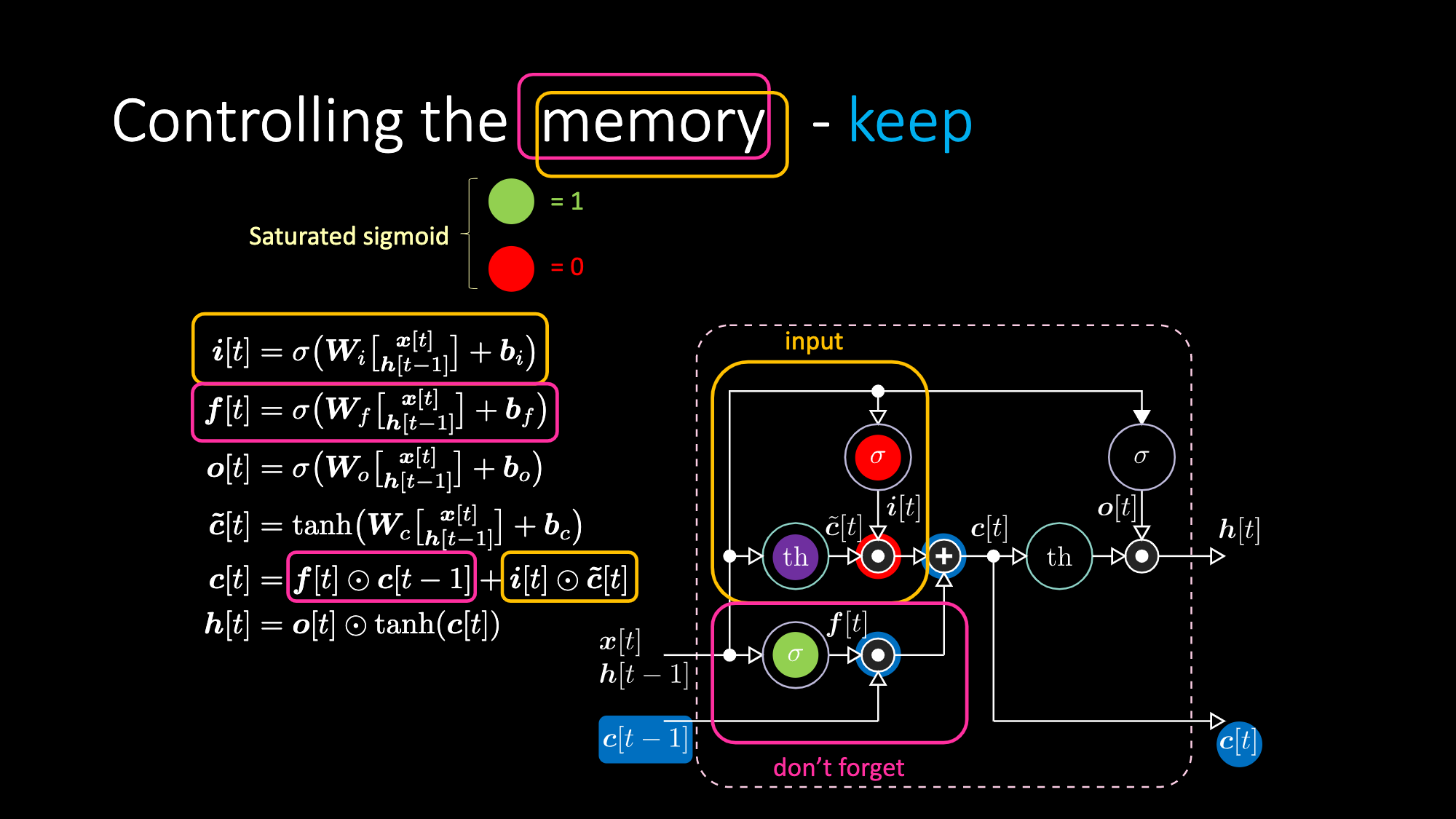
図27: LSTMのアーキテクチャ - メモリの保持

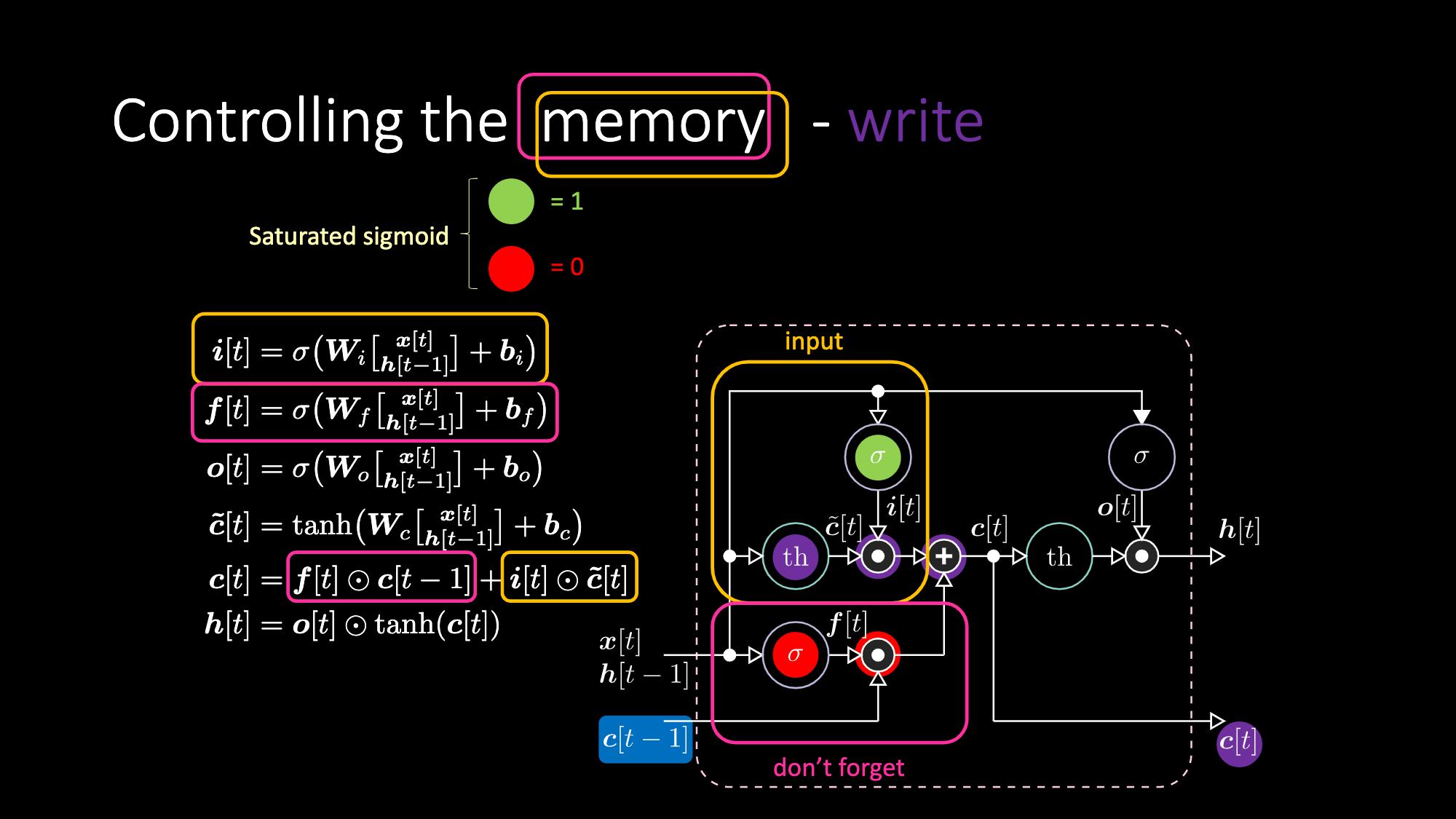
図28: LSTMのアーキテクチャ - メモリの書き込み

Notebookの例

シーケンスの分類

目的は，シーケンスを分類することです。要素とターゲットは、局所的に表現されます（0 以外のビットが 1 つだけの入力ベクトル）。シーケンスは、はBで始まり，E（「トリガーシンボル」）で終わります。それ以外の場合は、$t_1$と$t_2$の１の要素を除いた、集合 {a, b, c, d} の中からランダムに選ばれたシンボルで構成されます。DifficultyLevel.HARD の場合、配列の長さは100〜110の間でランダムに選ばれ、$t_1$ は10〜20の間でランダムに選ばれ、$t_2$ は50〜60の間でランダムに選ばれます。配列には、Q, R, S, U の4つのクラスがあり、これはX, Y の時間的順序に依存します。次のようなルールです。：X, X -> Q; X, Y -> R; Y, X -> S; Y, Y -> U

1). データセット探索

データ生成器からの戻り値の型は、長さ2のタプルです。 タプルの最初の項目は、$(32, 9, 8)$の形をしたシーケンスのバッチです。これがネットワークに投入されるデータです。各行には8つの異なるシンボル(X, Y, a, b, c, d, B, E)があります。各行はone-hotベクトルです。行のシーケンスはシンボルのシーケンスを表します。最初の全ての要素がゼロの行はパディングです。シーケンスの長さがバッチの最大長よりも短い場合にパディングを使用します。 タプルの2番目の項目は、4つのクラス（Q, R, S, U）があるので、シェイプが$(32, 4)$の対応するクラスラベルのバッチです。最初のシーケンスは BbXcXcbE です。すると、そのデコードされたクラスラベルは $[1, 0, 0, 0]$ であり、Qに対応します。

図29: 入力ベクトルの例

2). モデルの定義と訓練

単純なリカレントネットワーク、LSTMを作成し、10エポック訓練してみましょう。訓練のループでは、常に5つのステップを行います。

• モデルの順伝播を実行する
• 損失を計算する
• 勾配のキャッシュをゼロにする
• 誤差逆伝播によってパラメータに関しての損失の偏微分を計算する
• 勾配の反対方向にステップを踏む

図30: 単純なRNN vs LSTM - 10エポック

10エポック後に、簡単なタスクでは、RNNは50%の精度を得るのに対し、LSTMは100%の精度を得ることができます。しかし、LSTMはRNNの4倍の重みを持っており、2つの隠れ層を持っているので、公平な比較ではありません。100エポック後のRNNの精度も100%となりますが、LSTMよりも学習に時間がかかります。

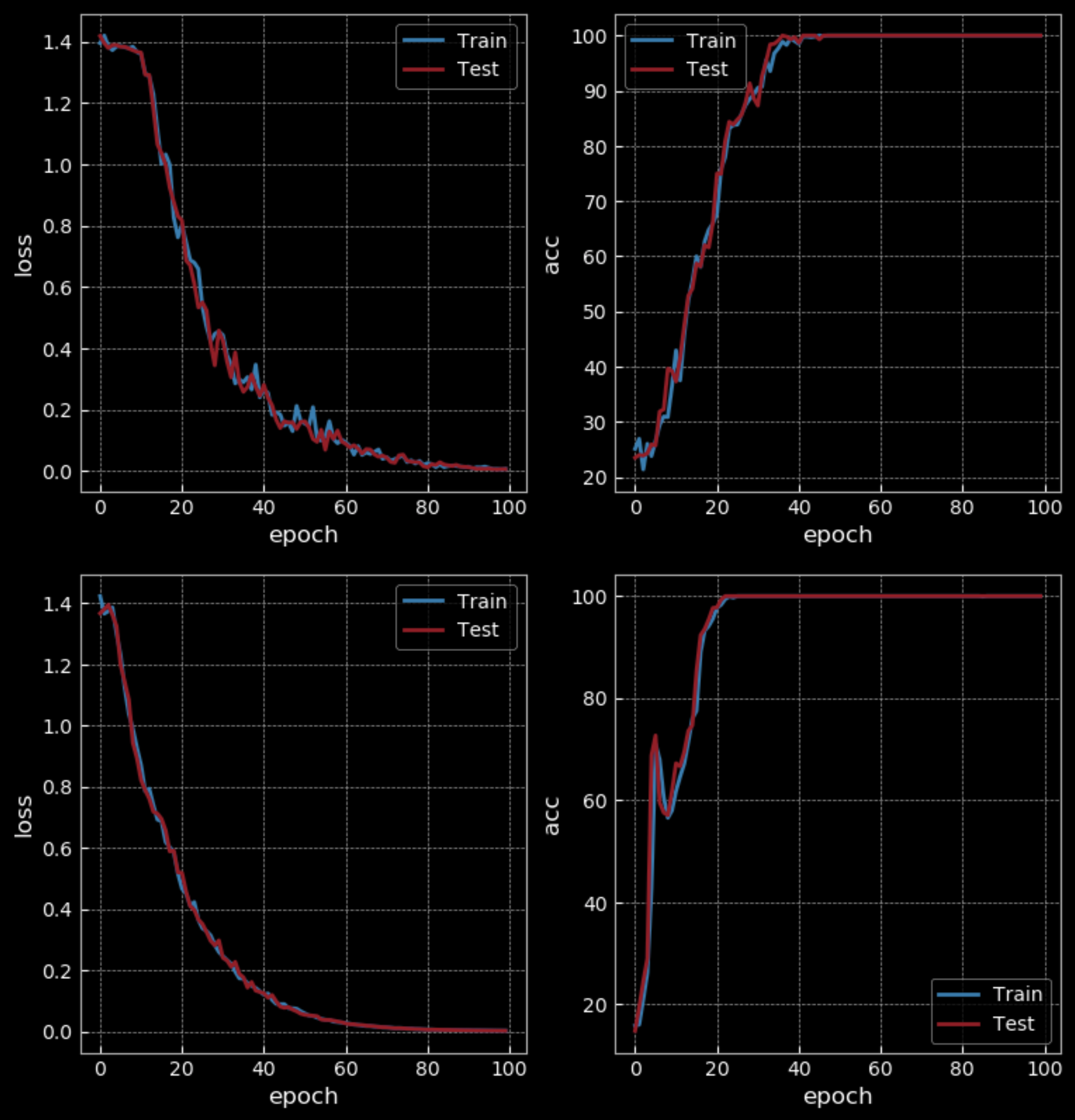
図31: 単純なRNN vs LSTM - 100エポック

タスクの難易度を上げる（長いシーケンスを使う）と、LSTMが学習し続けている間にRNNが失敗することがわかります。

図32: 隠れ状態の値の可視化

上の可視化は、LSTMにおける隠れ状態の時間変化を描いたものです。入力が$-2.5$以下であれば$-1$に、$2.5$以上であれば$1$にマップされるように、tanhを通して入力を送ります。つまり、この場合、特定の隠れ層が X (図の5行目) にピックされて、もう1つの X を得るまで赤くなっていることがわかります。つまり、セルの5番目の隠れユニットは、Xを観察すると活性化し、他のXを見た後は静かになるということです。これにより、シーケンスのクラスを識別することができます。

信号のエコー

信号のnステップのエコー処理は、同期化された多対多のタスクの一例です。例えば、第1入力シーケンスは "1 1 0 0 1 0 1 1 0 0 0 0 0 0 0 0 1 1 1 1 ..." であり、第1ターゲットシーケンスは "0 0 0 1 1 0 0 1 0 1 1 0 0 0 0 0 0 0 0 1 ..." です。この場合、出力は3ステップ後になります。つまり、情報を保持するためには短時間のワーキングメモリが必要となります。一方、言語モデルでは、まだ言われていないことを言っています。

シーケンス全体をネットワークに送り、最終的なターゲットを何かに強制する前に、長いシーケンスを小さなチャンクにカットする必要があります。新しいチャンクを送りながら、隠れ状態を追跡し、次の新しいチャンクを追加するときに内部状態への入力として送る必要があります。LSTMでは、十分な容量があれば長時間メモリを保持することができます。RNNでは、一定の長さに達すると過去のことを忘れ始めます。