RNNs, GRUs, LSTMs, Attention, Seq2Seq, and Memory Networks

深層学習のアーキテクチャ

深層学習では、異なる機能を実現するための異なるモジュールが存在します。深層学習の専門知識は、特定のタスクを行うためのアーキテクチャを設計することを含みます。 初期のコンピュータに指示を与えるためのアルゴリズムでプログラムを書くのと同様に、深層学習では複雑な機能を機能モジュールのグラフ（動的な場合もある）に還元し、その機能は学習によって最終的に決定されます。

畳み込みニューラルネットワークで見たものと同様に、ネットワークアーキテクチャが重要です。

リカレントニューラルネットワーク(RNN)

畳み込みニューラルネットワークでは、モジュール間のグラフや相互接続にループを持つことはできません。出力を計算するときに入力が利用できるように、モジュール間には少なくとも部分的な順序が存在します。

図1に示すように、リカレントニューラルネットワークにはループがあります。

図1 ループを持つリカレントニューラルネットワーク

• $x(t)$ : 時間を通じた入力
• $\text{Enc}(x(t))$: 入力の表現を生成するエンコーダー
• $h(t)$: 入力の表現
• $w$: 学習可能パラメータ
• $z(t-1)$: 前の時間ステップの出力に対応する、前の時間の隠れ状態
• $z(t)$: 現在の隠れ状態
• $g$: 複雑なニューラルネットワークになりうる関数。入力の一つは $z(t-1)$ であり、これは前の時間ステップの出力。
• $\text{Dec}(z(t))$: 出力を生成するデコーター

リカレントニューラルネットワーク：ループを展開する

ループを時間方向に展開します。入力は系列$x_1, x_2, \cdots, x_T$です。

"
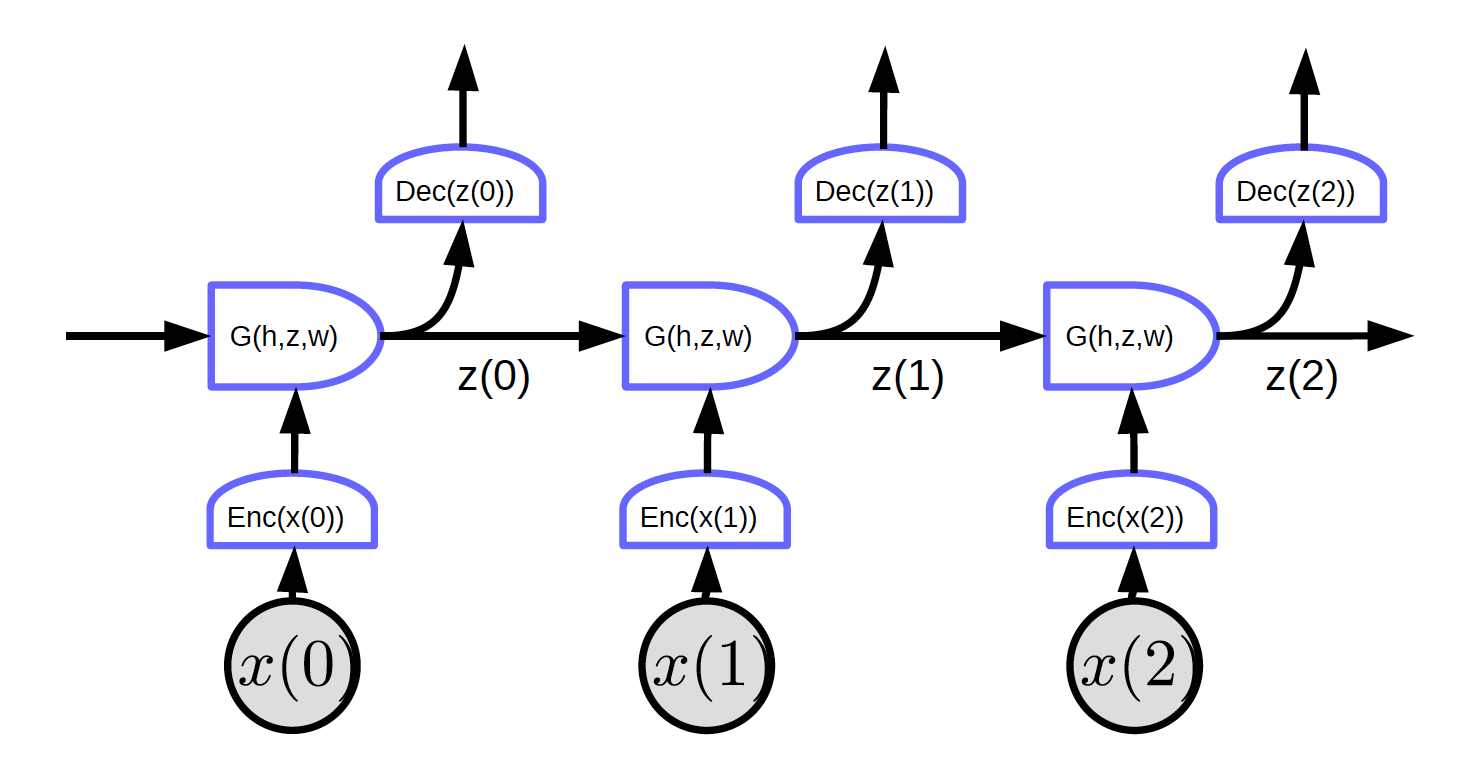
図2：ループが展開されたリカレントニューラルネット

図2において、入力は$x_1, x_2, x_3$です。

時刻$t=0$のとき、入力$x(0)$をエンコーダに渡し、表現$h(x(0)) = \text{Enc}(x(0))$を生成し、それを$G$に渡して隠れ状態$z(0) = G(h_0, z’, w)$を生成します。$t = 0$のとき、$G$の$z’$は、$0$として初期化してもいいですし、ランダムに初期化してもいいです。z(0)$はデコーダに渡されて出力が生成され、次の時間ステップにも渡されます。

このネットワークにはループがないので、誤差逆伝播を実装することができます。

図2は、1つの特殊な特徴を持つ通常のネットワークを示しています：すべてのブロックが同じ重みを共有しています。3つのエンコーダ、デコーダ、G関数はそれぞれ異なる時間ステップで同じ重みを持っています。

BPTT（Backprop through time）: 時間方向まで含めた誤差逆伝播のことです。残念ながら、ナイーブな形式のRNNでは、BPTTはあまりうまく機能しません。

RNNの問題点

1. 勾配消失
   • 長いシーケンスでは、勾配は時間ステップごとに重み行列（の転置）に乗算されます。重み行列の値が小さい場合、勾配のノルムは指数関数的に小さくなります。
2. 勾配爆発
   • 大きな重み行列があり、リカレント層の非線形関数の出力が飽和していない場合、勾配は爆発的に増大します。これによって更新時に重みが発散します。勾配降下法が機能するためには、小さな学習率を使用しなければならないかもしれません。

RNNを使う理由の一つに、過去の情報を記憶できるという利点があります。しかし、仕掛けのない単純なRNNでは、かなり前の情報を記憶するのには失敗する可能性があります。

勾配消失がある例

入力はCプログラムの文字です。システムはそれが構文的に正しいプログラムであるかどうかを判断します。構文的に正しいプログラムは、有効な数の中括弧と括弧を持っていなければなりません。したがって、ネットワークは、チェックすべき開いている括弧と中括弧の数を覚えていて、それらが最終的にすべて閉じているかどうかを確認しなければなりません。ネットワークはそのような情報をカウンターのような隠れた状態で記憶しなければなりません。 しかし長いプログラムでは、勾配消失のために、そのような情報を保存することに失敗してしまいます。

RNNのコツ

• 勾配クリッピング (勾配爆発を避ける)： 勾配が大きくなりすぎた場合には勾配を潰します。
• 初期化 (うまく初期状態を定めると、爆発や消失を避けることができます)： ある程度ノルムを維持するような、重み行列の初期化をします。例えば、直交初期化では、重み行列をランダムな直交行列として初期化します。

乗算モジュール

乗算モジュールでは、入力の加重和だけを計算するのではなく、入力の積を計算し、その積の加重和を計算します。

$x \in {R}^{n\times1}$, $W \in {R}^{m \times n}$, $U \in {R}^{m \times n \times d}$ そして $z \in {R}^{d\times1}$とします。 ここで U はテンソルです。

ただし$s_i = w_{i}^\top x = \sum_j w_{ij}x_j$です。

システムの出力は、入力と重みの古典的な加重和です。重み自体もまた、入力と重みの加重和です。

ハイパーネットワークアーキテクチャ：重みは別のネットワークによって計算されます。

Attention

$x_1$ と $x_2$ はベクトル、 $w_1$ と $w_2$ は softmax 後のスカラーで、 $w_1 + w_2 = 1$、 $w_1$ と $w_2$ は 0 から 1 の間の値です。

$w_1x_1 + w_2x_2$ は、 $x_1$ と $x_2$ を係数 $w_1$ と $w_2$ で加重したものです。

$w_1$と$w_2$の相対的な大きさを変えることで、$w_1x_1 + w_2x_2$の出力を、$x_1$または$x_2$、または$x_1$と$x_2$のいくつかの線形の組み合わせに切り替えることができます。

入力は、複数の $x$ ベクトル（$x_1$ と $x_2$ 以上）を持つことができます。attentionメカニズムは、ニューラルネットワークが特定の入力にattentionを向けさせ、他の入力を無視することを可能にします。

Attentionは、transformerアーキテクチャや他のタイプのattentionを使用する NLP システムでますます重要になってきています。

z はデータに依存しないので、重みはデータに依存しません。

Gated Recurrent Units (GRU)

上述したように、RNNは勾配消失/爆発に苦しみ、あまり長く状態を記憶することができません。GRUsCho, 2014、は、これらの問題を解決しようとする乗算モジュールの応用です。これはメモリ付きリカレントニューラルネットの一例です（別のものとしてLSTMがあります）。GRUユニットの構造は以下の通りです。

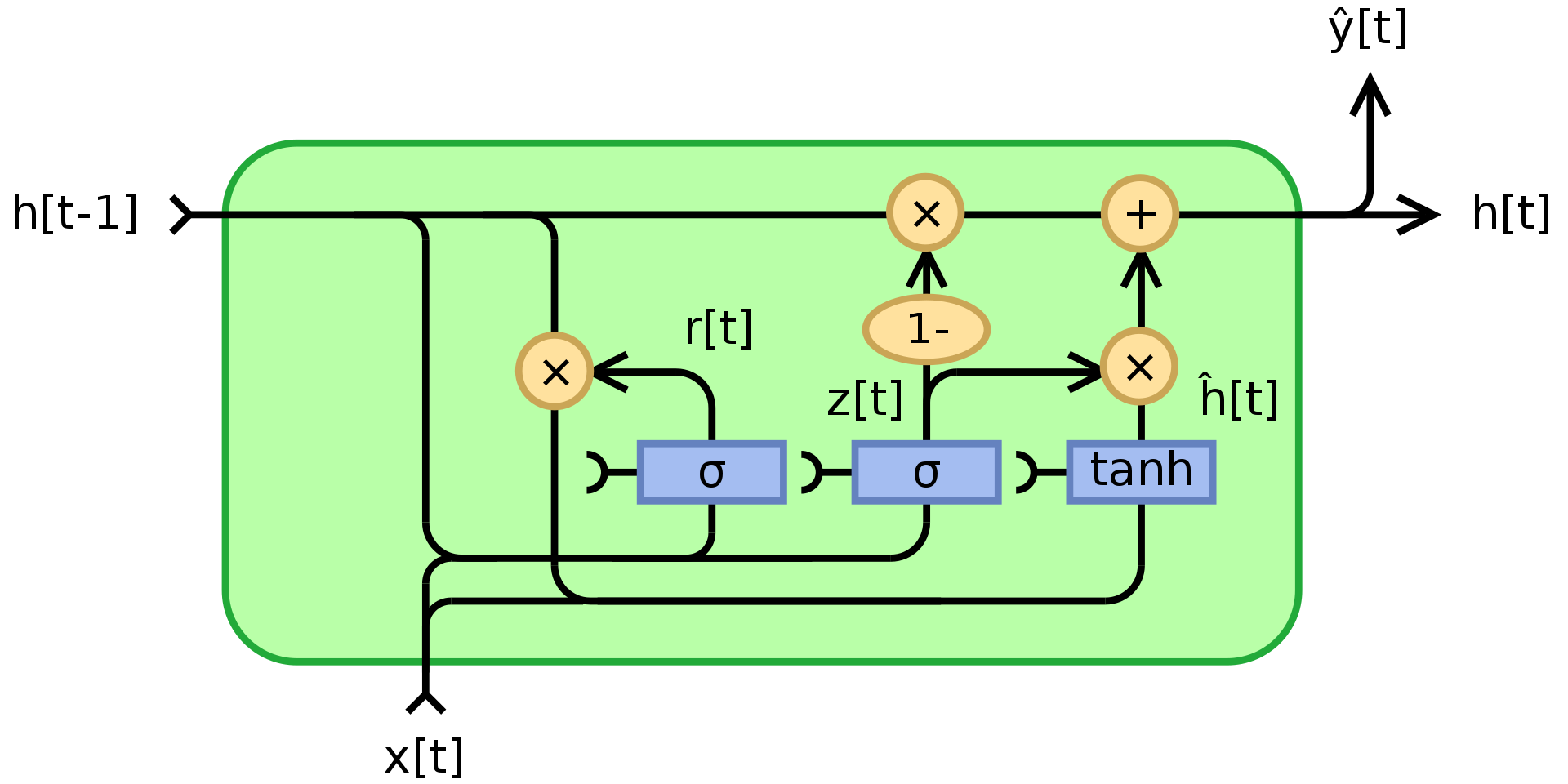
図3　Gated リカレントユニット

ここで、$\odot$は要素毎の乗算(アダマール積)、$x_t$は入力ベクトル、$h_t$は出力ベクトル、$z_t$は更新ゲートベクトル、$r_t$はリセットゲートベクトル、$\phi_h$はtanh、$W$,$U$,$b$は学習可能なパラメータです。

具体的には、$z_t$は、過去の情報を未来にどれだけ渡すべきかを決めるゲーティングベクトルです。これは、入力$x_t$と前の状態$h_{t-1}$に対する2つの線形層とバイアスの和にシグモイド関数を適用したものです。 $z_t$には、シグモイドを適用した結果として0と1の間の係数が含まれています。最終的な出力状態$h_t$は、$h_{t-1}$と$z_t$を介した$\phi_h(W_hx_t + U_h(r_t\odot h_{t-1}) + b_h)$の凸の組み合わせです。係数が1の場合、現在の出力は前の状態のコピーに過ぎず、入力を無視します(これがデフォルトの動作です)。係数が1より小さい場合は、入力からの新しい情報を考慮に入れます。

リセットゲート $r_t$ は、過去の情報をどれだけ忘れるかを決めるために使用されます。新しい記憶内容 $\phi_h(W_hx_t + U_h(r_t\odot h_{t-1}) + b_h)$において、$r_t$の係数が0であれば、過去の情報は何も記憶しません。同時に$z_t$が0ならば、$h_t$は入力を見ているだけなので、システムは完全にリセットされます。

LSTM (Long Short-Term Memory)

GRUは実はもっと前に出てきたLSTMの簡略版ですHochreiter, Schmidhuber, 1997。LSTMは、過去の情報を保存するためのメモリセルを構築することで、RNNの長期記憶喪失の問題を解決することも目的としています。LSTMの構造を以下に示します。

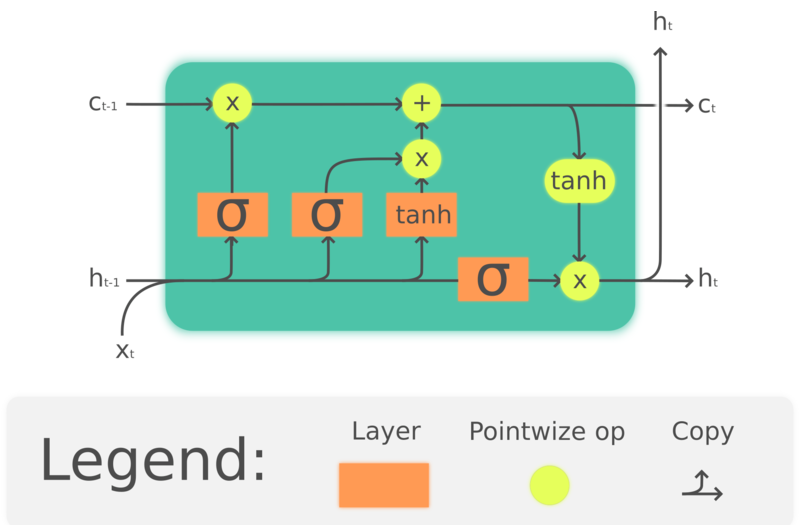
図4. LSTM

ここで、$\odot$は、要素毎の積、$x_t\in\mathbb{R}^a$は、LSTMユニットへの入力ベクトル、$f_t\in\mathbb{R}^h$は、忘却ゲートの活性ベクトル、$i_t\in\mathbb{R}^h$は、入力/更新ゲートの活性ベクトルです。また、$o_t\in\mathbb{R}^h$は、出力ゲートの活性ベクトル、$h_t\in\mathbb{R}^h$ は、隠れ状態ベクトル（出力としても知られている）、$c_t\in\mathbb{R}^h$ は、セルの状態ベクトルです。

LSTMユニットは、セルの状態$c_t$を使用して、ユニットを介して情報を伝達します。ゲートと呼ばれる構造を通して、セルの状態から情報をどのように保存したり削除したりするかを調節しています。忘却ゲート $f_t$ は、現在の入力と前の隠れ状態を見て、前のセルの状態 $c_{t-1}$ からどれだけの情報を残すかを決め、0から1の間の数を $c_{t-1}$ の係数として生成します。 そして、$\tanh(W_cx_t + U_ch_{t-1} + b_c)$は、セルの状態を更新するための新しい候補を計算し、忘却ゲートと同様に、入力ゲート$i_t$は、どの程度の更新を適用するかを決定します。最後に、出力$h_t$は、セルの状態$c_t$に基づいていますが、$\tanh$を通過し出力ゲート$o_t$によってフィルタリングされます。

LSTMは、NLPでは広く使われていますが、その人気は低下しています。例えば、音声認識では時間的なCNN、NLPではtransformerを使う方向に進んでいます。

Sequence to Sequence Model

Sutskever NIPS 2014によって提案されたアプローチは、古典的なアプローチに匹敵する性能を持った初めてのニューラル機械翻訳システムでした。これは、エンコーダとデコーダの両方が多層LSTMであるエンコーダ/デコーダアーキテクチャを使用しています。

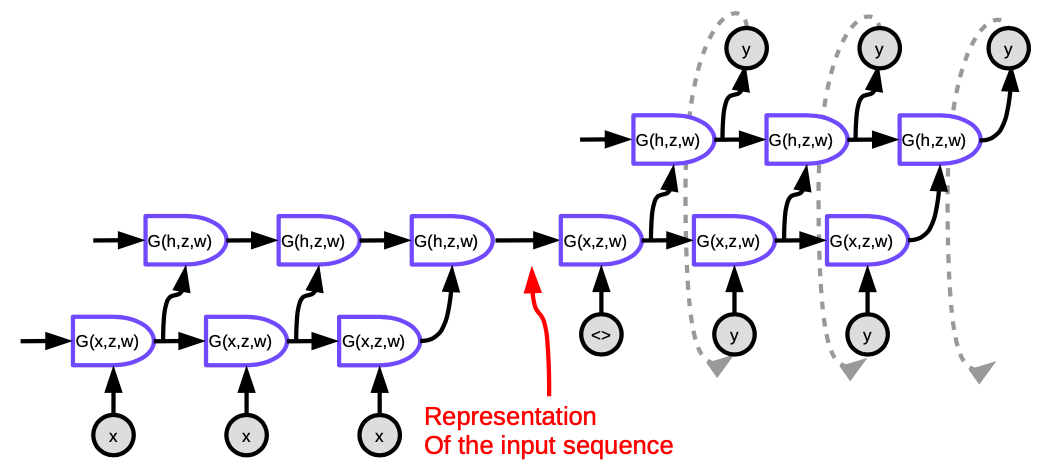
図5. Seq2Seq

図中の各セルはLSTMです。エンコーダ（左の部分）の場合、時間ステップ数は翻訳する文の長さに等しくなります。各ステップでは、前のLSTMの隠れ状態が次のLSTMにフィードされるLSTMのスタック（紙面では4層）があります。最後の時間ステップの最後の層では、文全体の意味を表すベクトルが出力され、それが別の多層LSTM（デコーダ）に送り込まれ、目的言語の単語が生成されます。デコーダでは、テキストは逐次的に生成されます。各ステップでは1つの単語が生成され、それが次の時間ステップへの入力として供給されます。

このアーキテクチャは、２つの点で満足できるものではありません。第一に、文全体の意味がエンコーダとデコーダの間の隠れた状態に押し込められなければなりません。第２に、LSTMは実際には約20語以上の情報を保持できません。これらの問題を解決する方法は、Bi-LSTMと呼ばれるもので、これは2つのLSTMを逆方向に実行するものです。 Bi-LSTMでは、意味は2つのベクトルで符号化され、1つは左から右にLSTMを実行して生成され、もう1つは右から左に実行されます。 これにより、あまり多くの情報を失うことなく、文の長さを2倍にすることができます。

AttentionつきSeq2seq

上記のアプローチの成功は短命でした。Bahdanau, Cho, Bengioによる別の論文では、文全体の意味を一つのベクトルに押し込むような巨大なネットワークを持つよりも、各時間ステップで、原語の中の同等の意味を持つ関連する場所だけに注意を集中させた方が、より意味があると提案しています（例えばattentionn機構を使うなどして）。

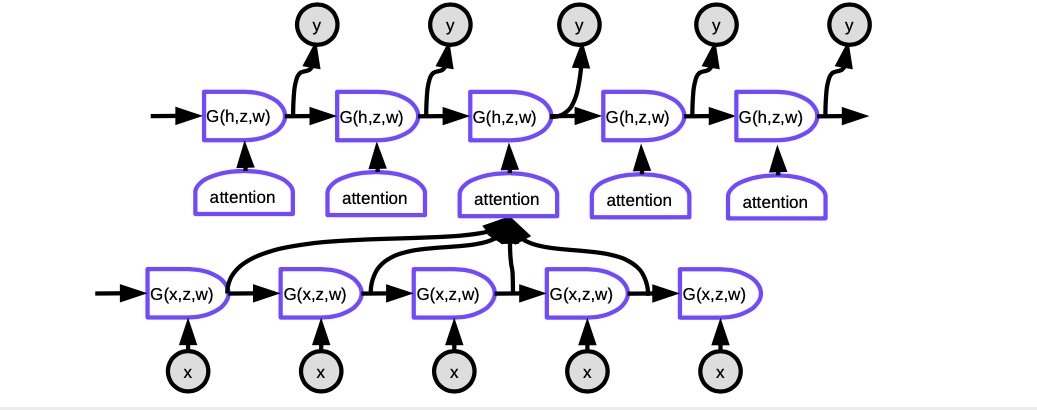
図6 AttentionつきSeq2seq

Attentionでは、各時間ステップで現在の単語を生成するために、まず、入力文中のどの単語の隠れ表現に注目するかを決定する必要があります。本質的には、ネットワークは、各エンコードされた入力がデコーダの現在の出力とどれだけ一致しているかをスコア化することを学習します。これらのスコアはソフトマックスで正規化され、係数は、異なる時間ステップでのエンコーダの隠れ状態の重み付けされた合計を計算するために使用されます。重みを調整することで、システムは焦点を当てる入力の領域を調整することができます。このメカニズムのすごいところは、係数を計算するために使用されるネットワークが誤差逆伝播によって学習できることです。手作業で構築する必要はありません!

Attention機構は、ニューラル機械翻訳を完全に変貌させました。その後、Googleは論文Attention Is All You Needを発表し、ニューロンの各層やグループがattentionを実装しているtransformerを発表しました。

Memory network

Memory networkは、2014年にAntoine Bordesと2015年にSainbayar Sukhbaatarによって開始されたFacebookでの研究に由来しています。

Memory networkのアイデアは、脳には2つの重要な部分があるということです。一つは長期記憶を司どる大脳皮質であり、もう一つは大脳皮質のほぼすべての場所にワイヤーを送っている海馬と呼ばれるニューロンの別の塊です。海馬は短期記憶に使われると考えられており、比較的短い期間の記憶をしています。海馬の容量が限られているため、睡眠時には長期記憶に固めるために海馬から大脳皮質に多くの情報が転送されているというのが定説です。

Memory networkには、ネットワークへの入力$x$(メモリのアドレスと考えてください)があり、この$x$とベクトル$k_1, k_2, k_3, \cdots$(キー)をドット積で比較します。それらをソフトマックスにかけると、要素の総和が1となる配列が得られます。 これらのベクトルにsoftmaxで得たスカラーを掛けて、これらのベクトルを合計すると (attention機構に似ていることに注意してください) 結果が得られます。

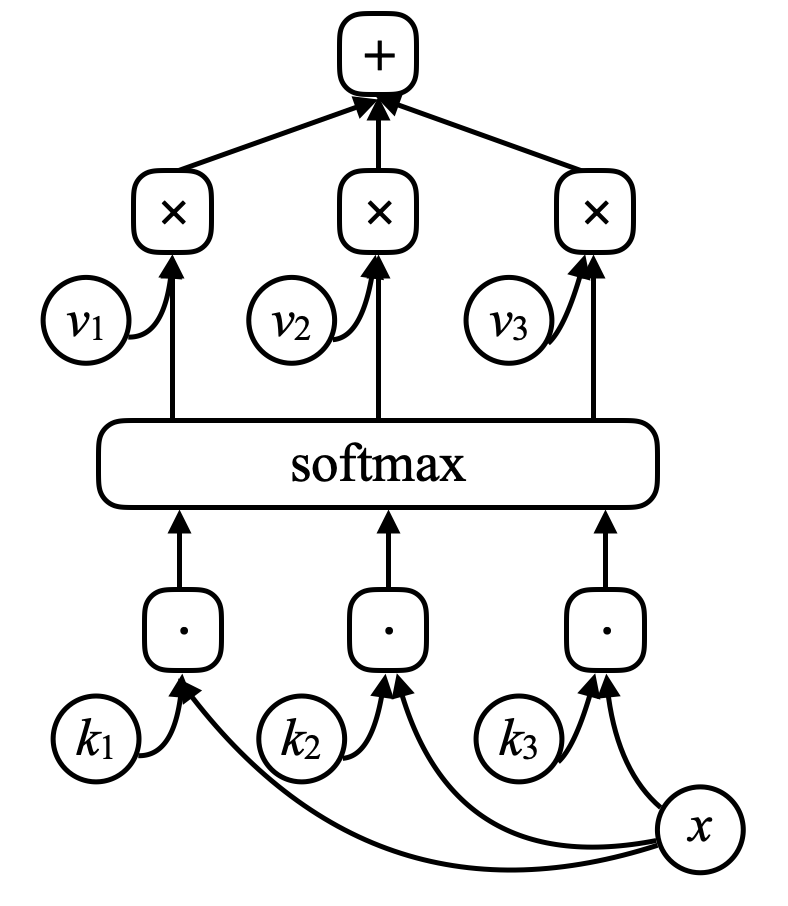
図7 Memory Network

キーの1つ(例えば $k_i$)が $x$ と完全に一致する場合、このキーに関連する係数は1に非常に近いものになります。したがって、システムの出力は本質的に $v_i$ となります。

これが アドレス指定可能な連想記憶 です。連想記憶とは、入力があるキーにマッチした場合、その値を取得することです。そして、これはそれの微分可能なバージョンにすぎず、誤差逆伝播したり、勾配降下法によってベクトルを変化させたりすることができます。

著者らが行ったことは、システムに一連の文章を与えることで、システムに文の内容を伝えることでした。文章は、事前に訓練されていないニューラルネットを通過することで、ベクトルにエンコードされ、記憶になります。システムに質問をすると、その質問をエンコードしてニューラルネットの入力として入れることで、ニューラルネットはメモリに対して$x$を生成し、メモリは値を返します。

この値は、ネットワークの前の状態と一緒に、メモリに再アクセスするために使用されます。そして、このネットワーク全体を訓練して、質問に対する答えを生成します。大規模な訓練の後、このモデルは実際に文の内容を記憶して質問に答えるように学習します。

Memory networkでは、入力を受けてメモリのアドレスを生成し、その値をネットワークに返してもらいます。そしてそれに続いて、最終的には出力を出すニューラルネットがあります。読み書きするためのCPUと外部メモリがあるので、これはコンピュータと非常によく似ています。

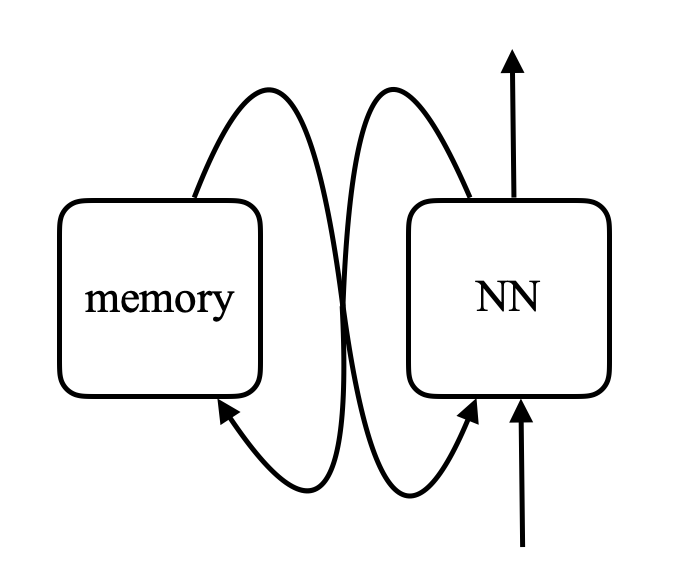
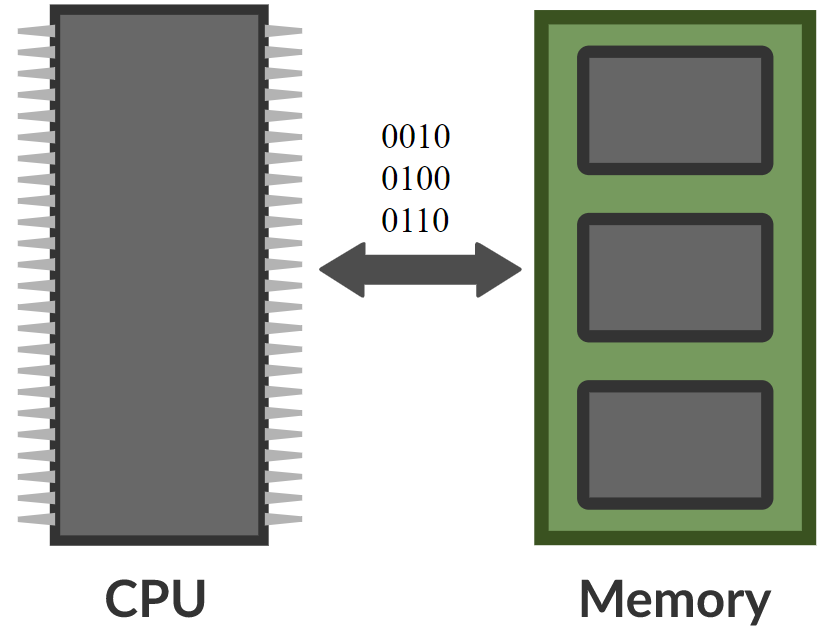
図8. memory networkとコンピュータの比較 (Photo by Khan Acadamy)

これを使って、実際に微分可能なコンピュータを作れるのではないかと想像している人たちがいます。その一例がDeepMindのNeural Turing Machineで、Facebookの論文がarXivで公開された3日後に公開されました。

入力をキーと比較し、係数を生成し、バリューを生成するというもので、transformerがやっていることは基本的にこれと同じです。 Transformerとは、ニューロンのすべてのグループがこれらのネットワークの1つであるようなニューラルネットワークのことです。