最適化テクニックII
🎙️ Aaron Defazioアダプティブ(適応的な)方法
モメンタムつき確率的勾配降下法(SGD)は、現在、多くの機械学習の問題に対する最先端の最適化手法のやりかたです。しかし、長年にわたって考え出され一般に適応的な方法と呼ばれる他の方法があって、これは悪条件の問題(SGDがうまくいかない場合)に対して特に役立ちます。
SGDでは、ネットワーク内のすべての重みは、同じ学習率(グローバル$\gamma$)を用いた式で更新されます。ここで、適応的な方法というのは、各重みの学習率を個別に適応させる方法のことをいいます。このために、各重みの勾配の情報も使用されます。
実応用上よく使用されるネットワークは、異なる部分に異なる構造を持っています。たとえば、CNNの入力層は大きな画像の非常に浅い畳み込み層であり、ネットワークの後半では、小さな画像の多数のチャネルの畳み込みで実現するようになっています。上記の操作は両方とも非常に異なっているため、前半の層に適用した学習率は、ネットワークの後半の層では必ずしも適用できない場合もあります。したがって、層ごとに適応的に学習率を微調整すると役立つ可能性があります。
ネットワークの後半部分(下の図1の4096)の重みは、出力を直接決定し、非常に強い影響を及ぼします。よって、それらにはより小さな学習率が必要です。対して、それより浅い層の重みは、特にランダムに初期化された場合、出力に対する個々の影響が小さくなります。
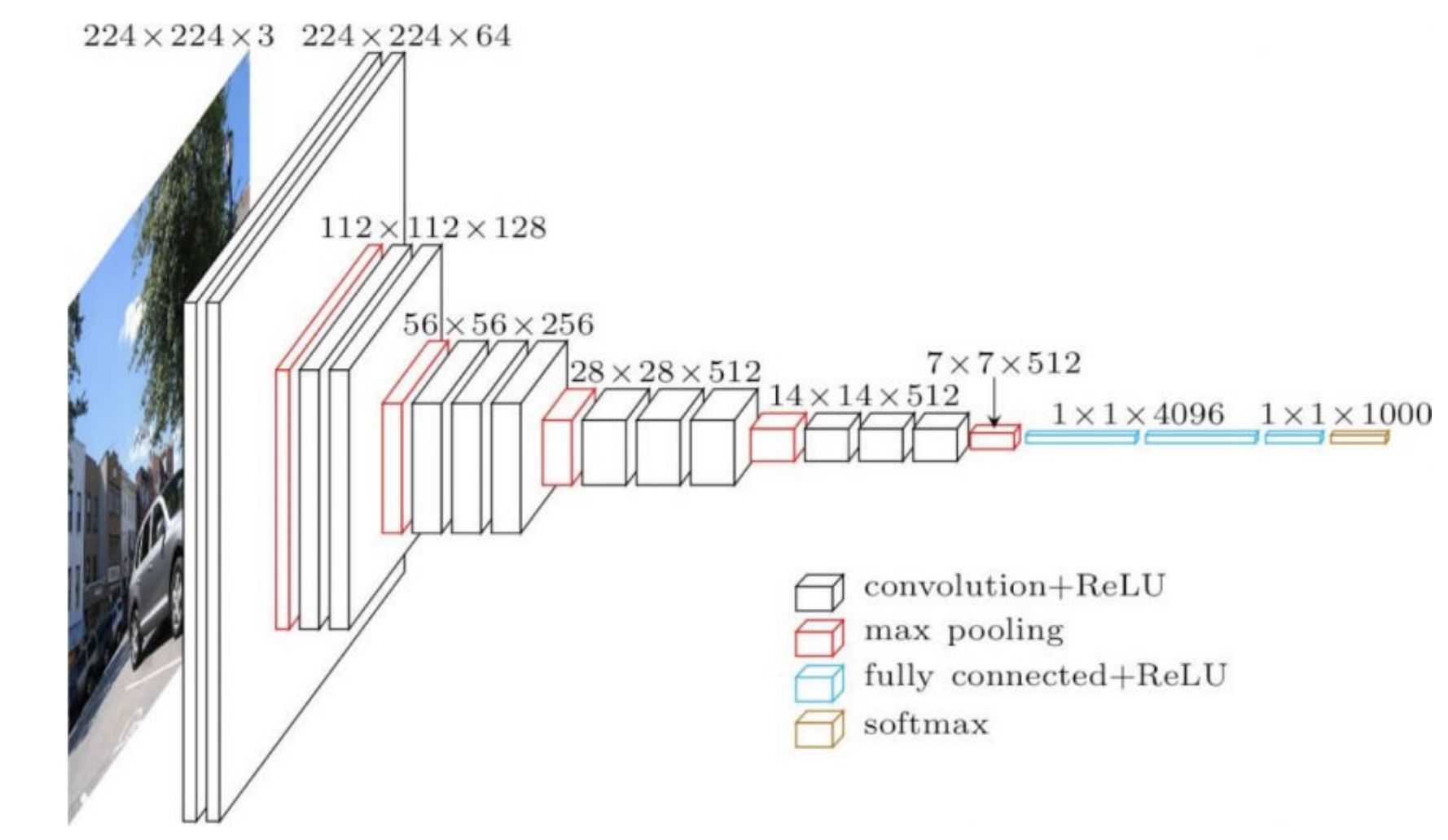
図1: VGG16
RMSprop
Root Mean Square Propagation(RMSProp,二乗平均平方根伝播) の重要なアイデアは、勾配が二乗平均平方根で正規化されることです。
以下の式で、勾配を2乗することは、ベクトルの各座標値を個別に2乗するということです。
\[\begin{aligned} v_{t+1} &= {\alpha}v_t + (1 - \alpha) \nabla f_i(w_t)^2 \\ w_{t+1} &= w_t - \gamma \frac {\nabla f_i(w_t)}{ \sqrt{v_{t+1}} + \epsilon} \end{aligned}\]ここで、$\gamma$はグローバルな学習率であり、 $\epsilon$はゼロ除算を回避するためにゼロに近い値($10^{-7}$または$10^{-8}$のオーダー)で設定され、 $v_{t + 1}$は2次モーメントの推定値です。
$v$を更新して、指数移動平均(時間とともに変化するある量を平均的に維持する標準的な方法)を介してこのノイズの量を推定します。新しい値はより多くの情報を提供しますので、より大きな重みを付ける必要があります。一つのやりかたは、古い値を指数衰減させることです。非常に古い$v$の値は、0から1の間の定数$\alpha$で各ステップで衰減させます。これにより、指数減衰させた古い値は、もう移動平均の計算に重要な部分ではなくなります。
元の方法では、中心化されていない2次モーメントで指数移動平均が保持されるため、ここでは平均を減算しません。 2次モーメントは、勾配を座標値ごとに正規化するために使用されます。つまり、勾配のすべての要素が2次モーメント推定値の平方根で除算されます。勾配の期待値が小さい場合、このプロセスは勾配を標準偏差で除算するのとほぼ同じです。
分母に小さな$\epsilon$を使用しても、$v$が非常に小さい場合、モメンタムも非常に小さいため、発散しません。
ADAM
ADAM、もしくはAdaptive Moment Estimation、適応的モーメント推定は、RMSpropにモメンタムをあわせる手法であり、より一般的に用いられています。 モメンタムの更新は指数移動平均に変換され、$\beta$を処理するときに一緒に学習率を変更する必要はありません。RMSpropの場合と同じく、ここでは勾配の2乗の指数移動平均を取ります。
\[\begin{aligned} m_{t+1} &= {\beta}m_t + (1 - \beta) \nabla f_i(w_t) \\ v_{t+1} &= {\alpha}v_t + (1 - \alpha) \nabla f_i(w_t)^2 \\ w_{t+1} &= w_t - \gamma \frac {m_{t}}{ \sqrt{v_{t+1}} + \epsilon} \end{aligned}\]ここの$m_{t+1}$はモーメントの指数移動平均です。
初期の反復計算時に移動平均を維持するためのバイアス補正は、ここには示されていません。
実際的な側面
ニューラルネットワークを訓練する場合、SGDは訓練プロセスの早期に間違った方向に進むことがよくありますが、RMSpropは正しい方向に向かうように補正をさせます。 ただし、RMSpropは通常のSGDと同じくノイズの影響を受けるため、極小値に近づくと、この極小値の周りで大幅に跳ね返ります。 SGDにモメンタムをつけるのと同じように、ADAMでも同じような改善が見られます。 ノイズの少ない最小値にたどり着けられるため、ADAMは一般的にRMSpropよりも推奨されます
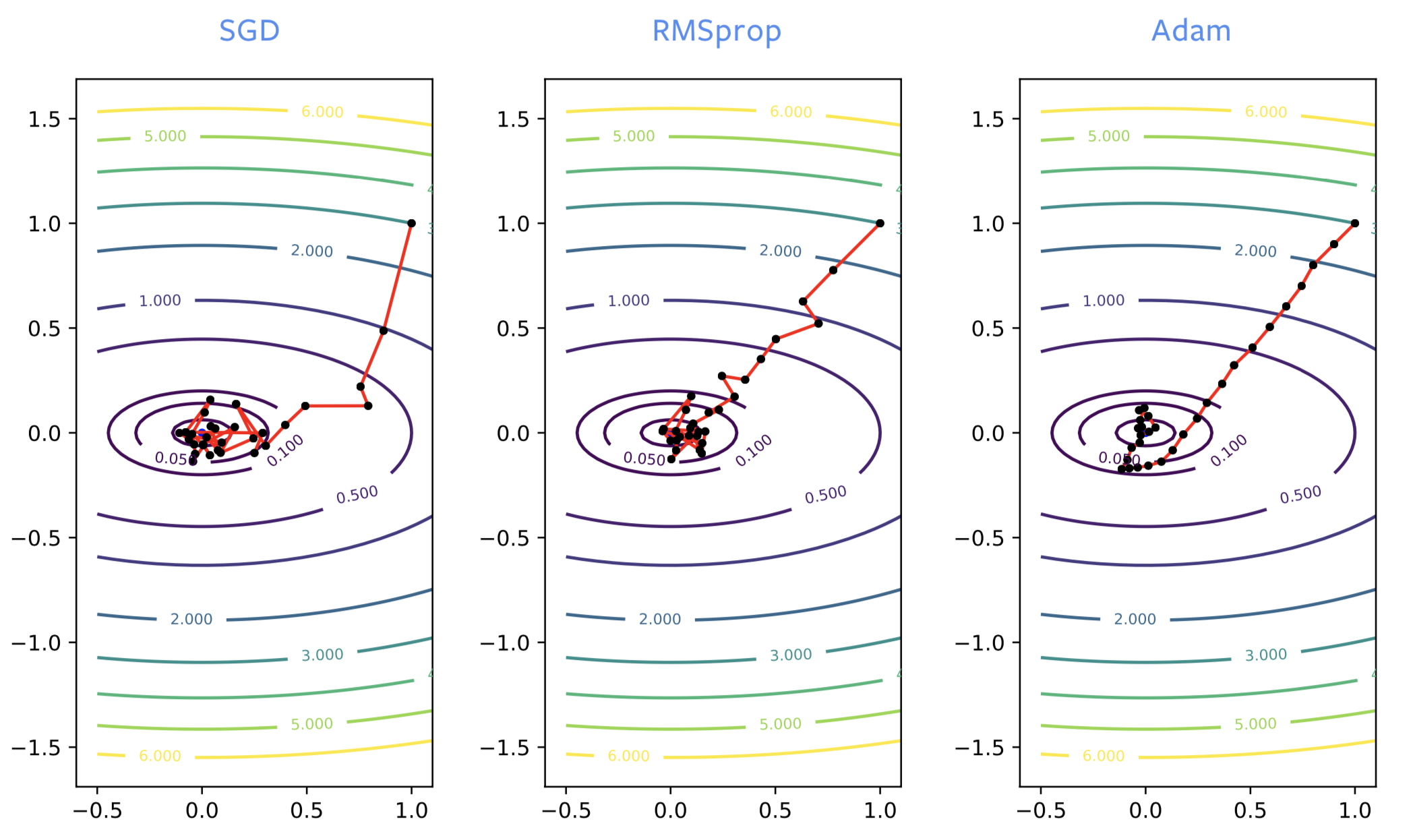
図2: SGD vs. RMSprop vs. ADAM
ADAMは、ニューラルネットを自然言語処理モデルとして用いるために訓練する上で、必要です。ニューラルネットワークを最適化するには、一般的にモーメント付きのSGDまたはADAMが推奨されます。ただし、論文に説明されたADAMの理論は十分に理解されておらず、いくつかの欠点もあります。
- 非常に単純なテスト問題で、収束しないこともあります。
- 汎化誤差を与えるとよく言われています。ニューラルネットワークが訓練用データに対して誤差を達成した場合、まだみたことない他のデータ点で訓練された損失はゼロになりません。特に画像の問題で、SGDを使用した場合よりも汎化誤差が悪化することがよくあります。より悪化する要因としては、ADAMが最も近い極小値を見つけること、ノイズの減少、またはその構造などが可能性として挙げられます。
- ADAMでは3つのバッファーを維持する必要がありますが、SGDでは2つのバッファーが必要です。数GBのサイズのモデルを訓練しない限り、これは実応用上は問題がありません。かえって、モデルはメモリに収まらない可能性があります。
- 1つではなく2つのモメンタムパラメータを調整する必要があります。
正規化層
最適化アルゴリズムを改善するより、正規化層はネットワーク構造自体も改善できます。 これらは、既存の層の間に追加される層です。 目標は、最適化と汎化のパフォーマンスを向上させることです。
ニューラルネットワークでは、通常、線性演算と非線性演算を交互に計算します。 非線形演算は、ReLUなどの活性化関数としてもよく知られています。 正規化層は、線形層の前、または活性化関数の後に配置できます。 最もよく行われる方法は、次の図のように、線形層と活性化関数の間に正規化層を配置することです。
|
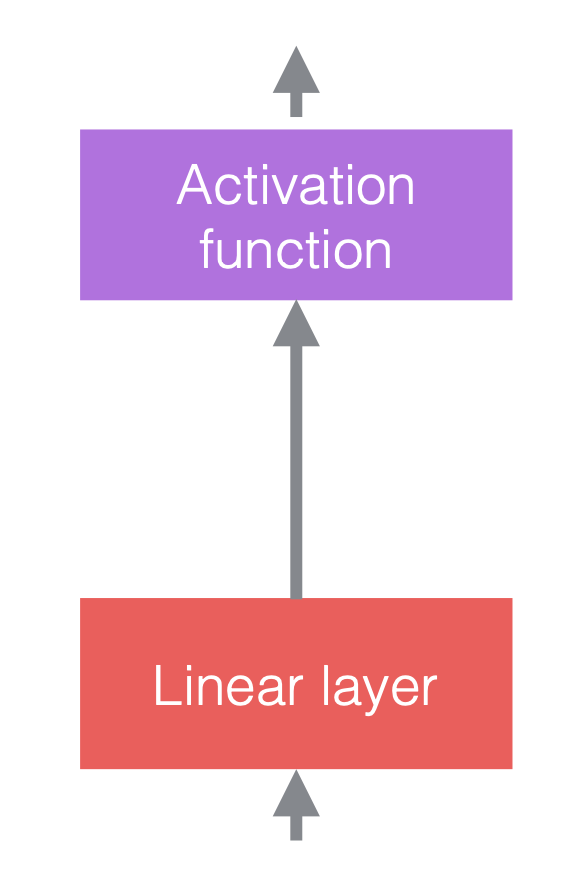
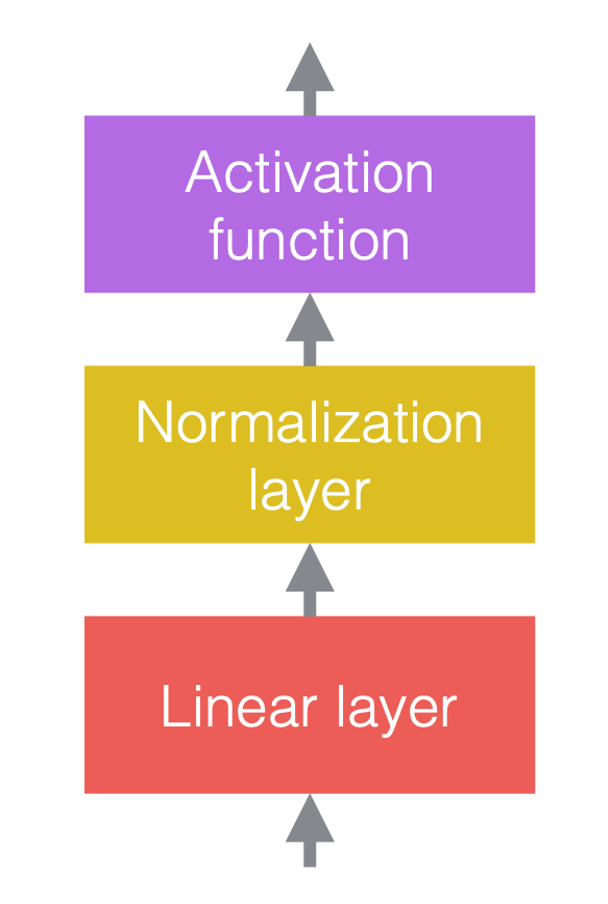
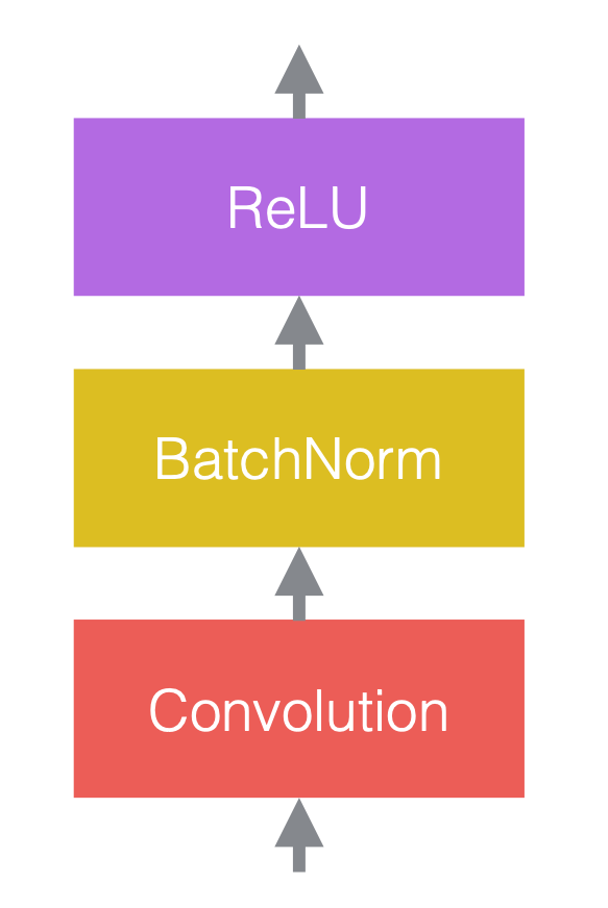
図3(c)では、畳み込みは線形層であり、その後にバッチ正規化がつながり、その後にReLUが続きます。
正規化層はネットワークを流れるデータに影響を与えますが、重みを適切に設定していれば、正規化されていないネットワークでも正規化されたネットワークと同じ出力を依然として出すことができるという意味で、正規化はネットワークの表現力を変化させることはありません。
ここで、$x$は入力ベクトル、$y$は出力ベクトル、$\mu$は$x$の平均の推定値、$\sigma$は$x$の標準偏差(std)の推定値です。 、$a$は学習可能なスケーリング係数であり、$b$は学習可能なバイアス項です。
学習可能パラメーターである$a$と$b$がない場合、出力ベクトル$y$の分布は平均0標準偏差値1に固定されます。スケーリング係数$a$とバイアス項$b$は、ネットワークの表現力は維持できます。つまり、出力値は特定の範囲を超える可能性があります。$a$と$b$は学習可能なパラメーターであり、$\mu$と$\sigma$よりもはるかに安定しているため、正規化を逆算できないことを注意してください。
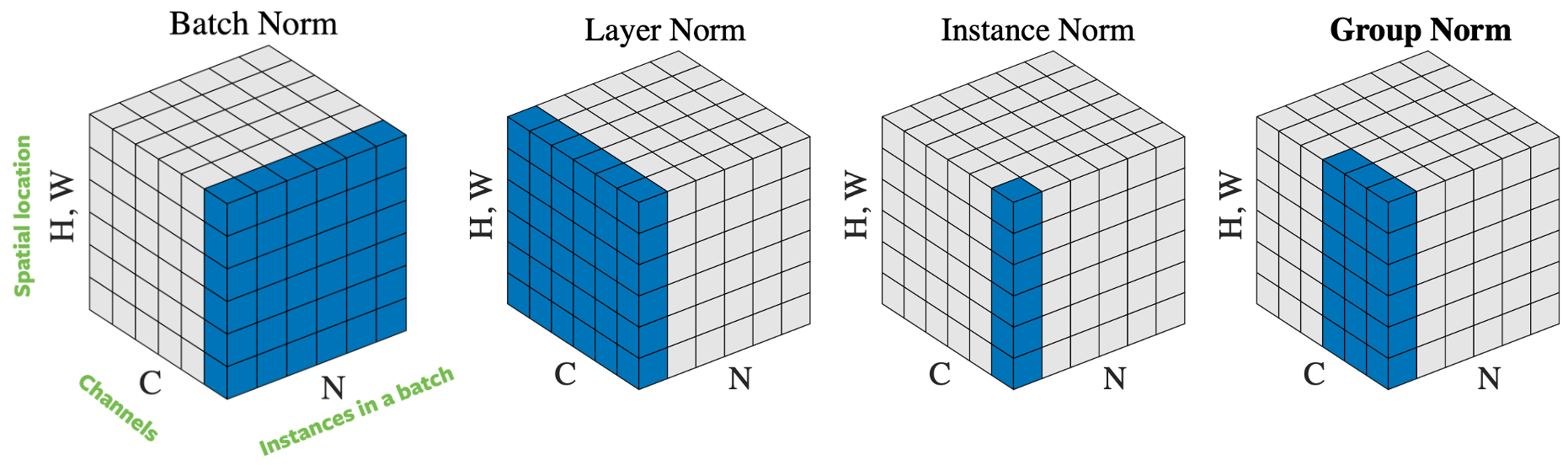
図4: 正規化の操作の詳細
正規化をしようとするサンプルの選択方法に基づいて、入力ベクトルを正規化する方法はいくつかあります。 図4は、高さ$H$と幅さ$W$でチャネル数の$C$ミニバッチ数$N$の画像の4つの異なる正規化アプローチを示しています。
- バッチ正規化:正規化が入力の1つのチャネルにのみ適用されます。これは最初に提案されたよく知られているアプローチです。詳細はResNet 7の訓練方法:バッチノルムを読んでください。
- レイヤー正規化:正規化がすべてのチャネルの1つの画像内に適用されます。
- インスタンス正規化:正規化が1つの画像と1つのチャネルにのみ適用されます。
- グループ正規化:正規化が1つの画像の多数のチャネルに適用されます。たとえば、チャネル0〜9はひとまとまりのグループであり、チャネル10〜19は別のグループです。実応用上は、グループサイズは32によく設定されます。これは、実際には優れたパフォーマンスを発揮し、SGDと競合しないため、Aaron Defazioが推奨するアプローチです。
実際には、バッチ正規化とグループ正規化はコンピュータビジョンの問題によく使われ、レイヤー正規化とインスタンス正規化は言語の問題によく使用されます。
正規化が役立つのはなぜですか?
正規化は実際にはうまく機能しますが、その有効性があるかどうかについてはまだ議論があります。もともとは、正規化は「内部共変量シフト」を減らすための提案でしたが、一部の学者は実験でそれが間違っていることを証明しました。にもかかわらず、正規化では明らかに次のいくつの要素が組み合わされています。
- 正規化層を備えたネットワークは最適化がより容易になり、より大きな学習率を使用できます。これによって、ニューラルネットワークの訓練を高速化する最適化効果があります。
- バッチ内のサンプルのランダム性のため、平均/標準推定値にノイズがあります。この余分な「ノイズ」により、場合によってはモデル汎化性能がよくなります。正規化には正則化効果があります。
- 正規化により、重みの初期化に対する感知度が低下します。
その結果、正規化により、もっと「注意深くならなくてよく」なります。つまり、条件がいかに悪いかを考慮せずとも ほとんどすべてのニューラルネットワークのビルディングブロックスが組み合わせて高い訓練性を得ることができるのです。
実用上考慮すべき点
正規化の適用に加えて、平均と標準偏差計算した上でバックプロパゲーションを行うというのが重要です。そうしなければ、訓練が発散してしまうからです。バックプロパゲーションの計算はかなり難しく、エラーが発生しやすくなりますが、PyTorchは自動的に計算できるため、非常に役立ちます。 PyTorchの2つの正規化層クラスを以下に示します。
torch.nn.BatchNorm2d(num_features、...)
torch.nn.GroupNorm(num_groups、num_channels、...)
バッチ正規化は最初に開発された方法であり、最もよく知られていますが、Aaron Defazio(講師)は、代わりにグループ正規化を使用することをお勧めします。より安定していて、理論的には単純で、よく効くといわれています。グループサイズ32が適切な初期値でよいでしょう。
バッチ正規化とインスタンス正規化の場合、複数の訓練サンプルを正規化するため、訓練したあと使用される平均/標準偏差はネットワークが評価されるたびに再計算されるのではなく定数となります。それに対して、グループ正規化とレイヤー正規化は単一サンプルで正規化されるため必要ありません。
[最適化の死](https://www.youtube.com/watch?v=-NZb480zlg&t=4817s)
時々、自分が何も知らない業界に入り込んで、そこ現在やっていることを改善することができます。そのような例の1つは、磁気共鳴画像法(MRI)の画像の再構成を加速するためのディープニューラルネットワークの使用です。

図5: うまくいくことがある!
磁気共鳴画像(MRI)再構成
従来のMRI再構成問題では、生データがMRI装置から取得され、単純なパイプライン/アルゴリズムを使用して画像が再構成されます。 MRI装置は、1行または1列を数ミリ秒ごとに2次元フーリエドメインでデータを取得します。この生データは周波数と位相チャネルにある各自のサイン波の幅から構成されています。簡単に言えば、それは実数と虚数のチャネルを同時に持つ複素数の画像のことです。この入力に逆フーリエ変換を適用すると、つまり、サイン波の値の重みを合計すると、元の解剖学的画像を取得することができます。
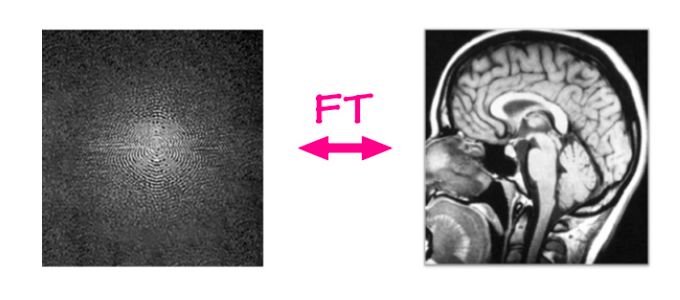
図6: MRIの再構成
現在、画像の大きさを問わず、フーリエ領域から画像領域に移動するための線形写像が存在しますが、これは非常に効率的です。文字通り数ミリ秒以内で行われます。しかし、これはより速く生成できるのか問題です。
生成加速化MRI
解決する問題は加速MRIです。加速というのは、MRI再構成プロセスをどうやって高速化にするのかです。マシンをより高速に運行し、それでもほぼ同じ品質の画像を生成できるようにしたいと考えています。1つの方法であり、またこれまで最も成功した方法は、MRIスキャンからすべての列をキャプチャしないという考えでした。そこでは、画像のいくつかのランダムにスキップすのですが、画像の真ん中に多くの情報が含まれているため、これは実用上は役に立ちます。しかしそうすると、問題として、線形写像で画像を再構築するのはできなくなってしまいます。図7の右端の画像は、サブサンプリングされたフーリエ空間に適用された線形写像の出力を示しています。ここからわかるように、この方法ではあまり有用な出力量が得られません。明らかにもう少し賢くやって改善する余地がありそうです。

図7: サブサンプルされたフーリエ空間上の線形写像
圧縮センシング
理論数学における最大の進歩の1つは、圧縮センシングでした。 Candes et al。この論文は、理論的には、サブサンプリングされたフーリエドメインの画像から完全な再構成を取得できることを示しています。言い換えると、再構成しようとしている画像がスパースまたはスパースな構造である場合、より少ない数値で完全に再構築することが可能であるということです。しかし、これが効くためいくつかの実用上の制約があります。具体的には、ランダムサンプリングする必要はなく、まとまってないようにサンプリングする必要があります。実際には、ランダムにサンプリングされている場合が多いですが。さらに、列の全体ををサンプリングする時間はその列の半分と同じくらいかかるので、実際には列全体もサンプリングします。
もう1つの条件は、画像にスパース性が必要であるということです。スパース性とは、画像内に多数のゼロの値または黒いピクセルがあることを意味します。波長分解を行うと、生の入力はスパースに表現できるようになります。しかし、この分解でも、正確にきっちりとしたスパースな画像ではなく、ほぼスパースなものになります。したがって、このアプローチでは、図8に示すように、完全に再構成されないもののかなり良い程度の再構成が得られます。ただし、波長ドメインに見えた入力データが非常にスパースであるなら、間違いなく完全な再構成画像が得られます。
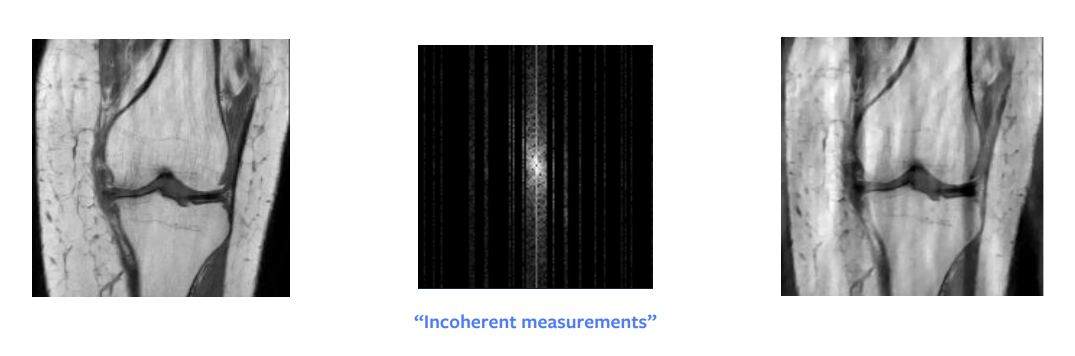
図8: 圧縮センシング
圧縮センシングの原理は、最適化の理論に基づいた方法です。 この再構成を取得する方法は、正則化項が追加された小さな最適化問題を解くことです。
\[\hat{x} = \arg\min_x \frac{1}{2} \Vert M (\mathcal{F}(x)) - y \Vert^2 + \lambda TV(x)\]ここで、$M$はサンプリングされていないデータを排除するマスク関数、$\mathcal{F}$はフーリエ変換、$y$はフーリエで変換されたデータ、$\lambda$は正則化ペナルティ係数、 $V$は正則化関数です。
よってこの最適化問題は、MRIスキャンのタイムステップごとに、または各「スライス」されたタイムごとに対して解かれなければなりません。これは、MRI自体のスキャンタイムより長い時間がかかることになります。この制約が、より良い方法を見つける理由になっています。
最適化はいつ必要なんですか?
各タイムステップで小さな最適化問題を解く代わりに、大きなニューラルネットワークを使用して解決するほうがいいんじゃないですか?という質問がわいてくるかもしれません。各タイムステップで最適化問題を解くことより十分な複雑さでニューラルネットワークを訓練して最適化問題を1つのステップで本質的に解決できるのは得だからです。
\[\hat{x} = B(y)\]ここで、$B$は深層学習モデルであり、$y$はフーリエ変換されたデータです。
15年前は、このアプローチは困難でしたが、現在では、これを導入する方が簡単になります。 図9は、この問題に対する深層学習アプローチの結果を示しています。出力は圧縮センシングアプローチよりとても優れており、実際のスキャンと非常によく似ていることがわかります。
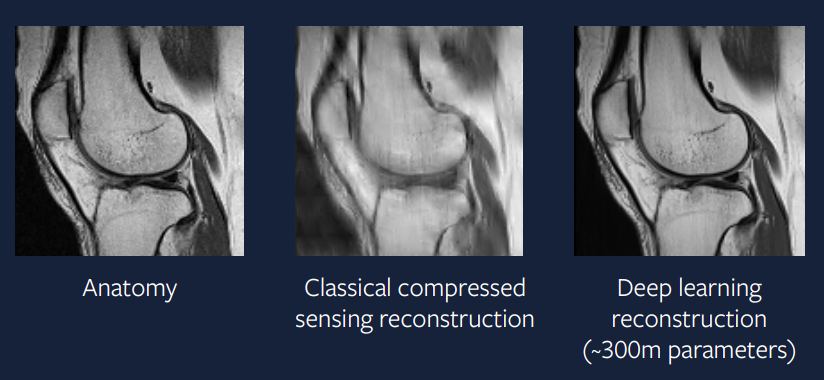
図9: 深層学習のアプローチ
この再構成の生成に使用されるモデルは、ADAMオプティマイザー、グループ正規化層、およびU-Netベースの畳み込みニューラルネットワークの組み合わせです。このようなアプローチは実際の応用の環境に非常に近く、このような加速されたMRIスキャンが数年以内に臨床診療で行われることを期待しています。
📝 Guido Petri, Haoyue Ping, Chinmay Singhal, Divya Juneja
Jesmer Wong
24 Feb 2020