最適化テクニックI
🎙️ Aaron Defazio勾配降下法
いろんな方法がありますが、その中で最も基本的だけれど最悪の(下記に説明する)方法である勾配降下法から、最適化手法の勉強を始めたいと思います。
問題
\[\min_w f(w)\]反復解法:
\[w_{k+1} = w_k - \gamma_k \nabla f(w_k)\]上記の
- $w_{k+1}$は $k$-回の繰り返しで更新された値、
- $w_k$は $k$-回の更新する前の初期値、
- $\gamma_k$はステップサイズ、
- $\nabla f(w_k)$は$f$の勾配。
ここでの前提は、関数$f$が連続的で微分可能であることです。 目的は、最適化関数の最低点(谷)を見つけることです。 ただし、この谷への実際の方向は不明です。 局所的に探ることしかできないため、負の勾配が私達が手に入れられる最適な情報です。 その方向に小さいステップサイズで進んで、近づいていくだけです。 小さな一歩を踏み出してから、再び新しい勾配を計算し、谷に到達するまでその方向に少しだけ移動します。 すると、本質的に勾配降下法が行っているのは、最も急な降下(負の勾配)の方向に向かうことだけです。
反復更新におけるこのパラメーター$\gamma$は、ステップサイズと呼ばれます。 最適なステップサイズの値は一般にわかりませんので、いろんな値を試す必要があります。 標準的な方法は、対数スケールで一連の値を試してから、最適な値を採用することです。
いくつかのシナリオが発生する可能性があります。上の画像は、パラメータが1次元の2次関数でのこれらのシナリオを示しています。 学習率が低すぎる場合、確実に最小値に進めますが、訓練時間が予想よりかなりかかる場合があります。
一般に、直接最小値に到達するステップサイズを選択することは非常に困難(または不可能)です。 このステップサイズという値は、最適値より少し大きいにするのが理想的です。 そうすると、実応用上は最も速く収束することができます。 逆に、学習率が大きすぎると、反復更新によって最小値から遠ざかり、発散してしまいます。 よって、学習率は発散するよりも少し小さいもの選択します。
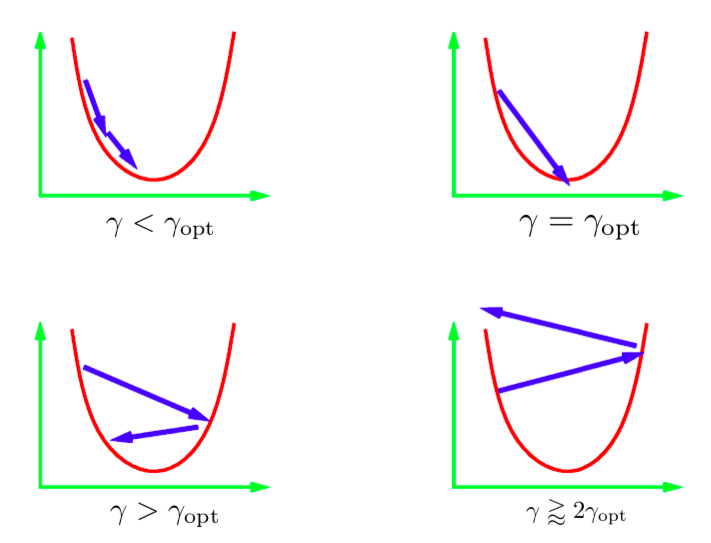
図1: 1次元の2次関数に対するステップサイズ
確率的勾配降下法
確率的勾配降下法では、実際の勾配ベクトルより確率的に推定された勾配ベクトルで計算します。 特にニューラルネットワークの場合、確率的推定とは、単一のデータ点(単一のインスタンス)での損失の勾配のことです。
$f_i$はニューラルネットワークの第$i$個のインスタンスの損失関数のことで、
\[f_i = l(x_i, y_i, w)\]最終的に最小化したい関数は、全てのインスタンスについての全体の損失である$f$です。
\[f = \frac{1}{n}\sum_i^n f_i\]確率的勾配降下法(SGD)では、$f_i$の勾配によって重みを更新します(総損失$f$の勾配で更新することではありません。)
\[\begin{aligned} w_{k+1} &= w_k - \gamma_k \nabla f_i(w_k) & \quad\text{(i は一様にランダムに選ばれる)} \end{aligned}\]$i$がランダムに選択された場合、$f_i$はノイズが多いものの、$f$の不偏推定量となります。これは数学的に次のように記述されます。
\[\mathbb{E}[\nabla f_i(w_k)] = \nabla f(w_k)\]これで、SGDの第$k$番目のステップの期待値は、フル勾配降下法の$k$番目のステップと同じになります。
\[\mathbb{E}[w_{k+1}] = w_k - \gamma_k \mathbb{E}[\nabla f_i(w_k)] = w_k - \gamma_k \nabla f(w_k)\]よって、SGDの更新は、フルバッチ更新と期待値の意味で同じです。 ただし、SGDは、単なるノイズを伴う勾配降下法ではありません。 SGDは高速であるだけでなく、フルバッチ勾配降下法よりも優れた結果を得ることができます。 SGDのノイズの部分は、浅い極小値を回避し、より良い(より深い)グローバルな最小値を見つけるのに役立ちます。 この現象はアニーリングと呼ばれます。
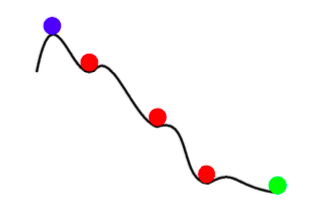
図2: SGDによるアニーリング
要約すると、確率的勾配降下法(SGD)の利点は次のとおりです。
- インスタンス間に多くの冗長な情報があります。 SGDは、これらの冗長な計算の多くを防ぎます。
- 初期段階では、勾配の情報と比較してノイズは小さいです。 したがって、SGDステップの降り方は普通の勾配降下法(GD)のステップとほぼ同じです。
- アニーリング: SGD更新のノイズにより、(浅い)グローバルではない極小値への収束が妨げられる可能性があります。
- 確率的勾配降下法は、計算量を大幅に削減できます(すべてのデータ点で計算しないため)。
ミニバッチ処理
ミニバッチ処理では、1つのインスタンスだけで計算するのではなく、ランダムに選択された複数のインスタンスでの損失を考慮します。 これにより、ステップ更新に伴うノイズが減少します。
\[w_{k+1} = w_k - \gamma_k \frac{1}{|B_i|} \sum_{j \in B_i}\nabla f_j(w_k)\]単一のインスタンスの代わりにミニバッチを使用することで、多くの場合ハードウェアをより有効活用できます。 たとえば、単一のインスタンスで訓練する場合、GPUを十分に活用することができません。 分散ネットワークで訓練するという技術では、マシンの大きなクラスターの間に大きなミニバッチを分割し、結果の勾配を集計します。 Facebookは最近、分散学習を使用して、1時間以内にImageNetデータでネットワークを訓練しました。
勾配降下法をフルバッチで使用してはならないことに注意することが重要です。 フルバッチサイズで訓練する場合は、LBFGSと呼ばれる最適化手法がおすすめです。 PyTorchとSciPyはどちらも、この手法の実装を提供しています。
モメンタム
モメンタムでは、更新パラメータは1個ではなく2個($p$と$w$)あります。 更新式は次のとおりです。
\[\begin{aligned} p_{k+1} &= \hat{\beta_k}p_k + \nabla f_i(w_k) \\ w_{k+1} &= w_k - \gamma_kp_{k+1} \\ \end{aligned}\]$p$はSGDモメンタムと呼ばれます。 各更新ステップで、係数$\beta$(0から1の間の値)によって衰減させてから、確率的勾配を古いモメンタムに追加します。 $p$は、勾配の移動平均値と考えることができるでしょう。 最後に、$w$を新しいモメンタム$p$の方向に移動します。
代替形式:確率的ヘビーボール法
\[\begin{aligned} w_{k+1} &= w_k - \gamma_k\nabla f_i(w_k) + \beta_k(w_k - w_{k-1}) & 0 \leq \beta < 1 \end{aligned}\]この形式は、前の形式と数学的に等価です。 ここで、次のステップは、前のステップの方向($w_k - w_{k-1}$)と新しい負の勾配の組み合わせです。
直観
SGDのモメンタムは、物理学におけるモメンタムの概念に似ています。 最適化プロセスは、重いボールを丘に転がすことと似ています。 モメンタムは、ボールがすでに移動しているのと同じ方向に移動し続けるようにしています。勾配は、ボールを他の方向に押す力と考えることもできるでしょう。

図3: モメンタムの効果
ソース: distill.pub
(左の図のように)進行方向を激しく変更するのではなく、モメンタムは適度に変更を行います。 モメンタムは、SGDのみを使用する場合に一般に生じる振動を衰減させます。
パラメーター$\beta$は衰減量と呼ばれます。 $\beta$はゼロより大きくなければなりません。ゼロの場合は、GDと同じだからです。 また、1未満である必要があります。そうでない場合、すべてが発散してしまいます。 $\beta$の値が小さいほど、方向の変更が速くなります。 値が大きいほど、ターンするのに時間がかかります。
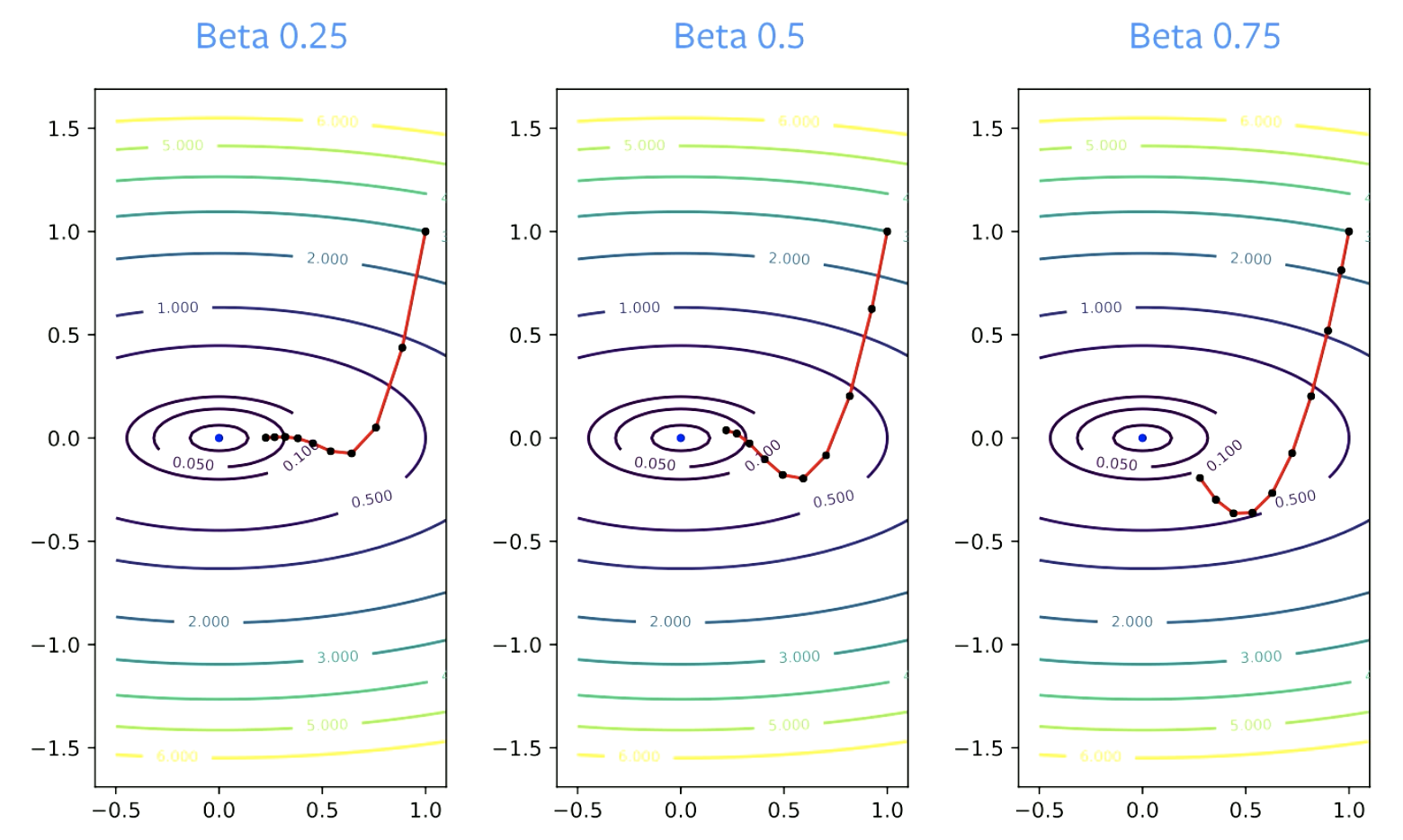
図4: βが収束に与える影響
実用上のガイドライン
モメンタムは、確率的勾配降下法で常に使用する必要があります。 $\beta$ = 0.9または0.99はほとんどの場合うまくいきます。
収束を維持するため、モメンタムパラメータを増やす一方、ステップサイズパラメータを減らす必要があります。 $\beta$が0.9から0.99に変更された場合、学習率を10分の1に減らす必要があります。
なぜモメンタムはうまくいくのか
加速度
以下は、ネステロフのモメンタムの更新則です。
\[p_{k+1} = \hat{\beta_k}p_k + \nabla f_i(w_k) \\ w_{k+1} = w_k - \gamma_k(\nabla f_i(w_k) +\hat{\beta_k}p_{k+1})\]ネステロフのモメンタムは,定数を慎重に選択すると、収束を加速できます。 ただし、これは凸最適化問題にのみ適用され、ニューラルネットワークには適用されません。
通常のモメンタムも加速された方法と言われていますが、実際には、二次関数に対して加速されるのみです。 また、SGDにはノイズがあり、加速はノイズではうまく機能しないため、加速はSGDではうまく機能しません。 したがって、モメンタムSGDには多少の加速がありますが、それだけでは、この手法の高性能を説明するのに適していません。
おそらく、より実際的でありうるあるモメンタムがうまくいく理由は、ノイズ平滑化です。
モメンタムは勾配を平均します。 これは、各ステップの更新に使用する勾配の移動平均です。
理論的には、SGDをうまく動かすには、すべてのステップの更新を平均する必要があります。
\[\bar w_k = \frac{1}{K} \sum_{k=1}^K w_k\]モメンタムを用いたSGDの優れている点は、この平均化が不要になったことです。 モメンタムは、最適化プロセスに平滑化を追加します。これにより、各更新が解の適切な近似になります。 SGDを使用すると、一連の更新を平均して、その方向に一歩踏み出すことができます。
加速とノイズ平滑化のおかげでモメンタムは高性能になっています。
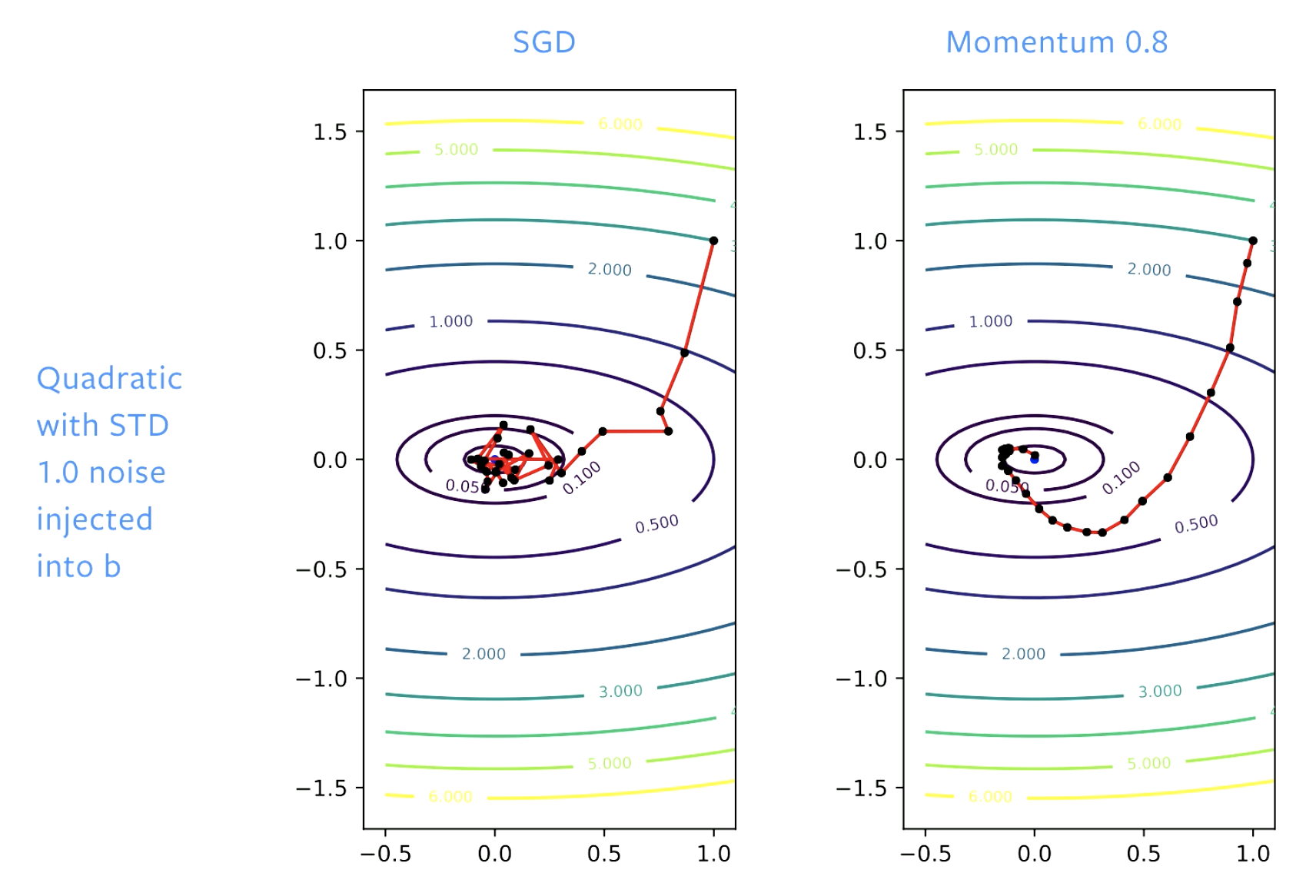
Figure 5: SGD vs. Momentum
SGDの場合、最初は解に向かって順調に進むのですが、ボウル(谷底)に到達すると、この床を跳ね回るようになります。学習率を調整すれば、跳ね回る速度は遅くすることができます。モメンタムを使えば、ステップを滑らかにすることで、跳ね回り自体をなくすことができます。
📝 Vaibhav Gupta, Himani Shah, Gowri Addepalli, Lakshmi Addepalli
Jesmer Wong
24 Feb 2020