Properties of natural signals

自然界の信号の性質

すべての信号は、ベクトルとして考えることができます。例えば、音声信号は1次元の信号$\boldsymbol{x} = [x_1, x_2, \cdots, x_T]$です。ただし、各$x_t$は時刻$t$での波形の振幅を表しています。誰かが何を話しているのかを理解するために、蝸牛はまず気圧の振動を信号に変換し、脳は言語モデルを使ってこの信号を言語に変換します。音楽の場合、信号は立体音響で、音が複数の方向から聞こえているように錯覚させるために2つ以上のチャンネルを持っています。2つのチャンネルを持っていても、時間だけが信号の変化に沿って変化しているので、1次元の信号であることに変わりはありません。

画像は、情報が空間的に描かれているので、２次元信号です。各点はそれ自体がベクトルであることに注意してください。つまり、画像の中に $d$ チャンネルがある場合、画像の各空間的な点は $d$ 次元のベクトルであることを意味します。カラー画像はRGBの平面を持っているので、 $d = 3$ ということになります。任意の点 $x_{i,j}$ について、これはそれぞれ赤、緑、青の色の強度に対応します。

上記の論理で言語を表現することもできます。各単語は、私たちの語彙の中で発生する位置に1を持ち、それ以外の場所では0を持つone-hotベクトルに対応しています。これは、各単語が語彙の大きさのベクトルであることを意味します。

自然データの信号は、以下の特性に従います。

1. 定常性：　特定のモチーフが信号全体に渡って繰り返されます。音声信号では、時間領域にわたって同じタイプのパターンが何度も何度も観察されます。画像では、同じような視覚的パターンが次元を超えて繰り返されることを意味します。
2. 局所性：　近くの点は遠くの点よりも相関が高くなります。1次元信号の場合、ある点 $t_i$ でピークを観測した場合、 $t_i$ の周りの小さな窓の中の点は $t_i$ と同じような値を持つと予想されますが、 $t_i$ から離れた点 $t_j$ では、 $x_{t_i}$ は $x_{t_j}$ との関係が非常に薄いことを意味しています。より正式には、信号と反転した信号の畳み込みは、信号が反転した信号と完全に重なったときにピークを迎えます。2つの1次元信号間の畳み込み(相互相関)は、2つのベクトルがどれだけ似ているか、あるいは近いかの指標である、互いのドット積以外の何ものでもありません。このように、情報は信号の特定の部分に含まれています。画像の場合、これは、画像内の2つの点の間の相関が、点を遠ざけるにつれて減少することを意味します。$x_{0,0}$ の画素が青である場合、次の画素($x_{1,0},x_{0,1}$)も青である確率はかなり高いですが、画像の反対側の端($x_{-1,-1}$)に移動するにつれて、この画素の値は $x_{0,0}$ の画素の値とは独立になります。
3. 構成性；　自然界に存在するすべてのものは、全体の部分のまた部分の・・・というように構成されています。例として、文字は文字列を形成して単語を形成し、それがさらに文を形成します。文は組み合わせて文書を形成することができます。構成性は世界を説明可能にします。

もしデータが定常性、局所性、構成性を示すならば、スパース性、重み共有、層の積み重ねを利用したネットワークでそれらを利用することができます。

不変性と等価性を生み出すために自然の信号の性質を活用する

局所性 $Rightarrow$ スパース性

図1は、5層の全結合ネットワークを示しています。各矢印は、入力に乗算される重みを表しています。見ての通り、このネットワークは非常に計算量が多いです。

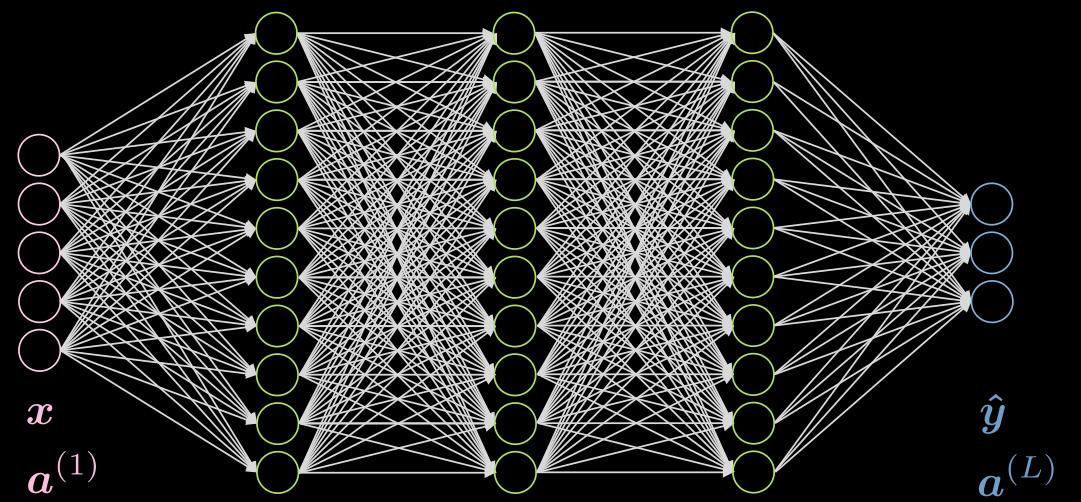
図1: 全結合ネットワーク

私たちのデータが局所性を示す場合、各ニューロンは、前の層の少数の局所ニューロンに接続する必要があります。そのため、図２に示すように、いくつかの接続を削除することができます。図2(a)は全結合ネットワークです。データの局所性を利用して、図2(b)では遠く離れたニューロン間の接続を落としています。図2(b)の隠れ層のニューロン(緑)は入力全体をカバーしているわけではありませんが、全体のアーキテクチャはすべての入力ニューロンをカバーすることができます。受容野（RF）は、特定の層の各ニューロンが見ることができる、あるいは考慮に入れた、前の層のニューロンの数です。したがって、隠れ層の出力層のRFは3、入力層のRFは3ですが、出力層のRFは5となります。

図2(a): スパース性を適用する前	図2(b): スパース性を適用した後

定常性　\Rightarrow$ パラメータ共有

データが定常性を示す場合には、ネットワークアーキテクチャー全体で小さなパラメータのセットを複数回使用することができます。例えば、図3(a)のスパースネットワークでは、3つの共有パラメータ（黄色、オレンジ、赤）のセットを使用することができます。そうすると、パラメータの数は9個から3個に減ってしまいます。新しいアーキテクチャは、これらの特定の重みを訓練するためのデータがより多くあるので、より良く機能するかもしれません。 スパース性とパラメータ共有を適用した後の重みは、畳み込みカーネルと呼ばれます。

図3(a): パラメータ共有適用前	図3(b): パラメータ共有適用後

以下は、スパース性とパラメータ共有を使用することの利点です。

• パラメータ共有
  • より速い収束
  • より良い汎化
  • 入力サイズに拘束されない
  • カーネルの独立性 $\Rightarrow$ 並列化
• 接続のばらつき
  • 計算量の削減

図４は、１次元データ上のカーネルの例を示しており、カーネルサイズは、２（カーネル数）×７（前の層の厚さ）×３（ユニークな接続の数／重さ）です。

カーネルサイズの選択は経験的なものです。3 * 3 の畳み込みが空間データの最小サイズであるように思われます。サイズ1の畳み込みは、より大きな入力画像に適用できる最終層を得るために使用することができます。偶数のカーネルサイズはデータの品質を低下させる可能性があるので、奇数のカーネルサイズ、通常は3や5を使用します。

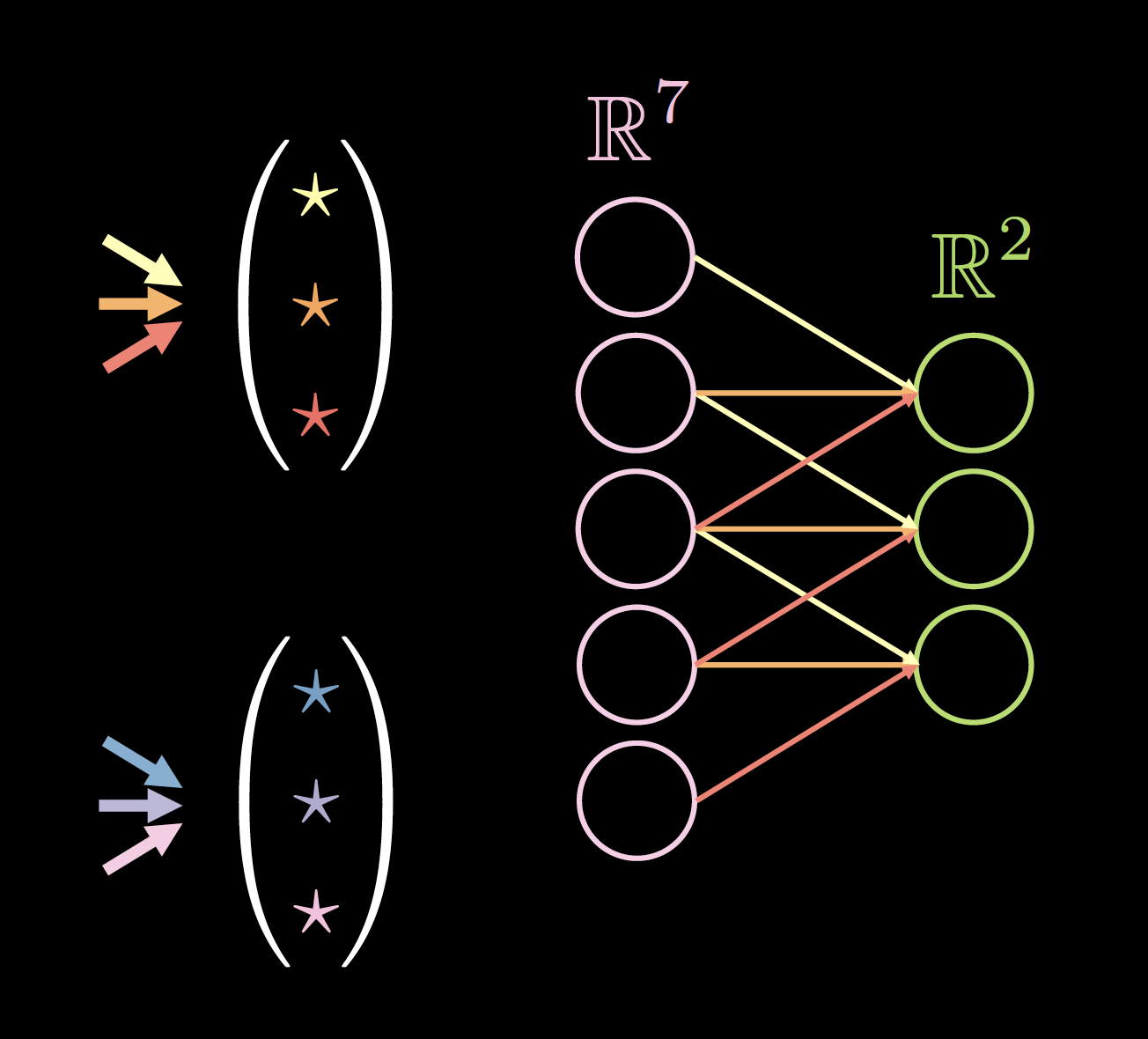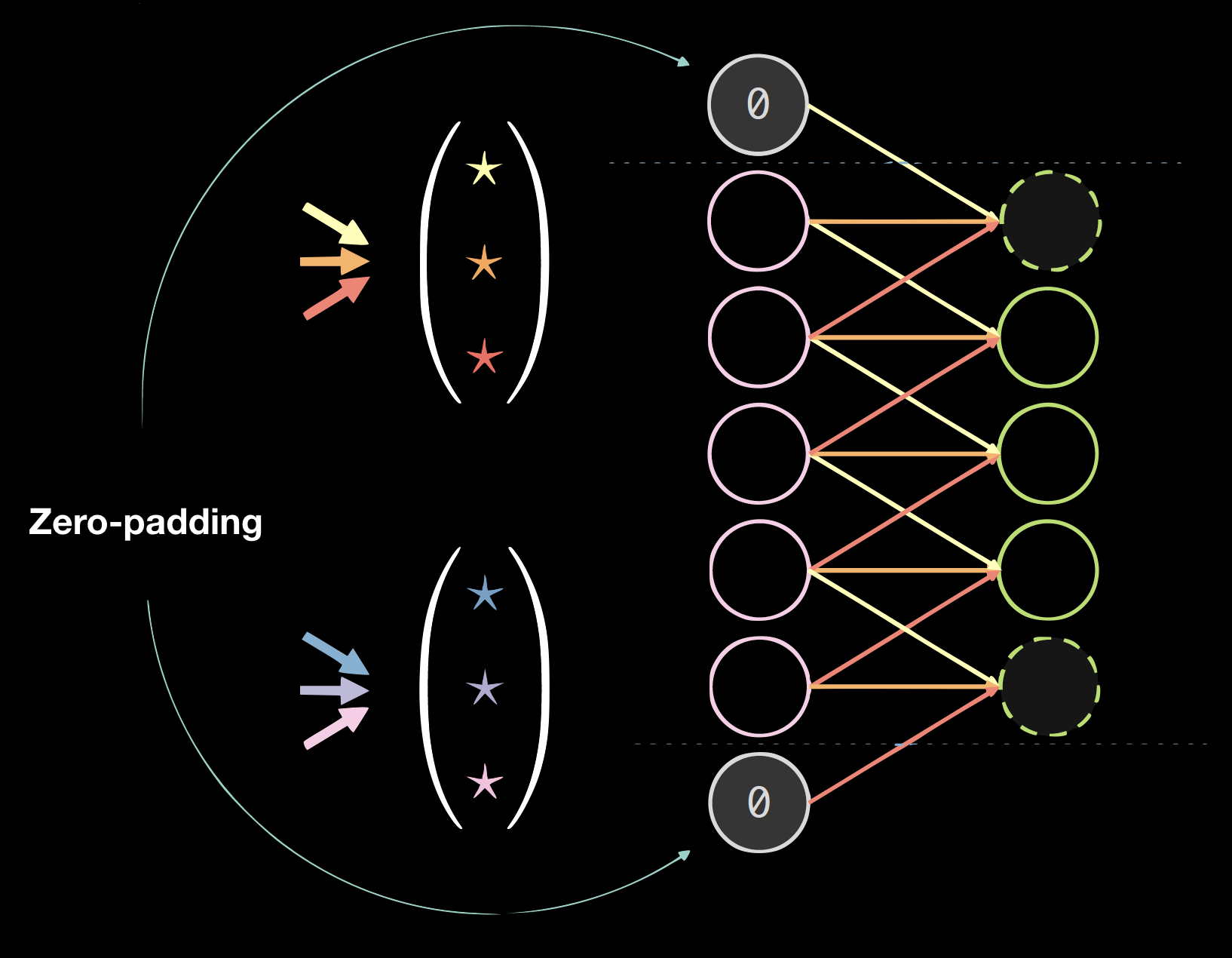図4(a): １次元データに対するカーネル	図4(b): ゼロパディングのデータ

パディング

パディングは一般的に最終的な結果に悪影響を与えますが、プログラム的には便利です。通常はゼロパディングを使用します。サイズ = (カーネルサイズ - 1)/2のようにします

標準的な空間的CNN

標準的な空間的CNNには以下の特性があります。

• 複数の層
  • 畳み込み
  • 非線形性(ReLUとLeaky ReLU)
  • プーリング
  • バッチ正規化
• Residual connection

バッチ正規化とresidual connectionは、ネットワークをうまく訓練するのに非常に役立ちます。 Residual connectionを介した追加の接続は、下から上へのパスと上から下への勾配のパスを保証します。

図5では、入力画像には2次元の空間情報がほとんど含まれていますが（各ピクセルの色である特徴情報は別として）、出力層は厚いです。途中で、空間情報と特徴情報の間にトレードオフが生じ、表現が密になります。したがって、階層が上がるにつれて、空間情報が失われ、表現が密になります。

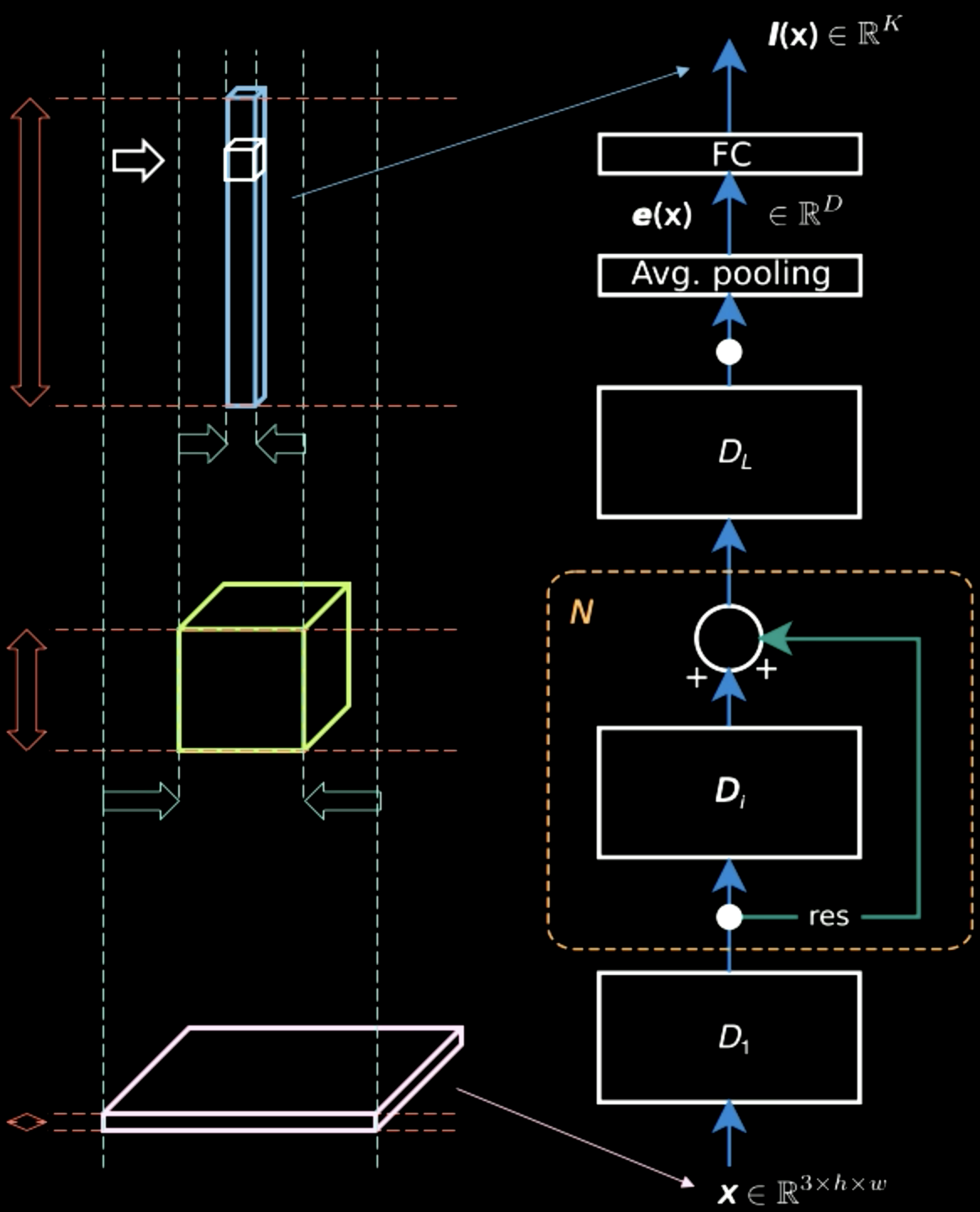
図5: 階層を移動する情報表現

プーリング

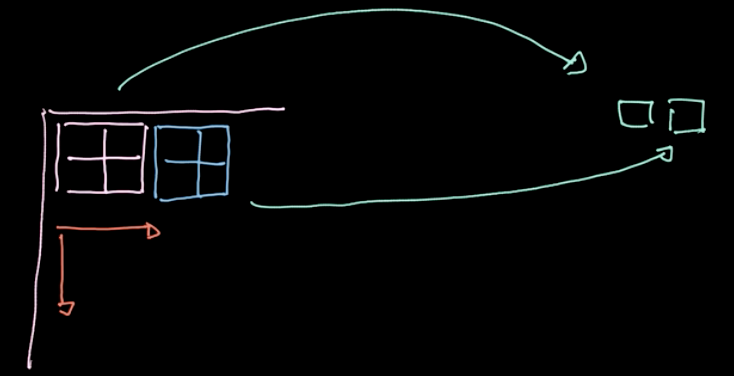
図6: プーリングの図

$L_p$-ノルムという演算子を、異なる領域に適用します（図6参照）。このような演算子は、1つの領域につき1つの値しか与えられません（今回の例では、4つの画素に対して1つの値を与えます）。次に、データ全体を領域ごとに繰り返していき、ストライドに基づいてステップを動かします。サイズ$m * n$ で $c$ チャネルを持つデータから始めると、 サイズ$\frac{m}{2} * \frac{n}{2}$ で$c$チャンネルを持つデータになります。図7を見てください。 プーリングはパラメトライズされていませんが、最大プーリングや平均プーリングなど、さまざまな種類のプーリングを選択することができます。プーリングの主な目的は、データ量を減らすことで、合理的な時間で計算できるようにすることです。

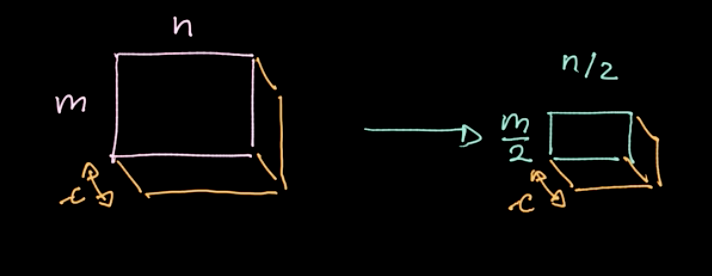
図7: プーリングの結果

CNN - Jupyter Notebook

Jupyter Notebookは ここ にあります。ノートブックを実行するには、README.md で指定された pDL 環境がインストールされていることを確認してください。

このノートでは、MNISTデータセットの分類タスクのために、多層パーセプトロン(FCネットワーク)と畳み込みニューラルネットワーク(CNN)を学習しています。なお、どちらのネットワークもパラメータ数は同じです。(図8)

図8: 元のMNISTデータセットからのインスタンス

訓練の前に、ネットワークの初期化がデータの分布と一致するようにデータを正規化します（非常に重要です！）。また、以下の5つの操作/ステップが訓練に存在することを確認してください。

1. モデルにデータを供給する
2. 損失の計算
3. 蓄積された勾配のキャッシュを zero_grad() でクリーニングする
4. 勾配の計算
5. オプティマイザーを使ってパラメータを更新する

まず、正規化されたMNISTデータを用いて両者のネットワークを学習します。その結果、FCネットワークの精度は$87\%$、CNNの精度は$95\%$でした。同じパラメータ数であれば、CNNはより多くのフィルタを学習することができました。FCネットワークでは、遠くにあるものと近くにあるものとの間に依存関係を持たせようとするフィルタが訓練されます。それらは完全に無駄になります。その代わりに、畳み込みネットワークでは、これらのパラメータはすべて隣のピクセル間の関係に集中しています。

次に、MNISTデータセットの全ての画像の全ての画素に対して、ランダムな並べ替えを行います。これにより、図8を図9に変換し、この修正されたデータセット上で両方のネットワークを訓練します。

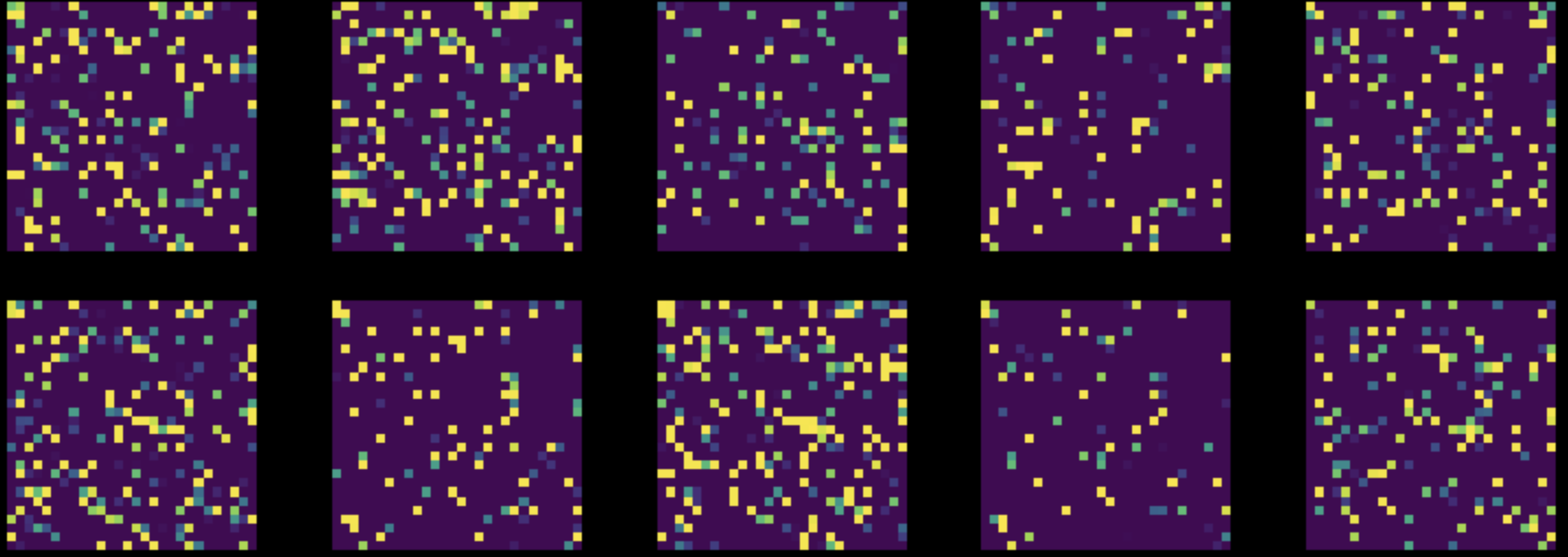
図9: Permuted MNIST Datasetからのインスタンス

FCネットワークの性能はほとんど変わらない($85\%$)ですが、CNNの精度は$83\%$に低下しました。これは、ランダムな並べ替えの後、画像がCNNで利用可能な局所性、定常性、構図性の３つの性質を保持しなくなったためです。