ニューラルネットワークのパラメータ変換の可視化と畳み込みの基礎概念

ニューラルネットワークの可視化

このセクションでは、ニューラルネットワークの内部動作の可視化を行います。

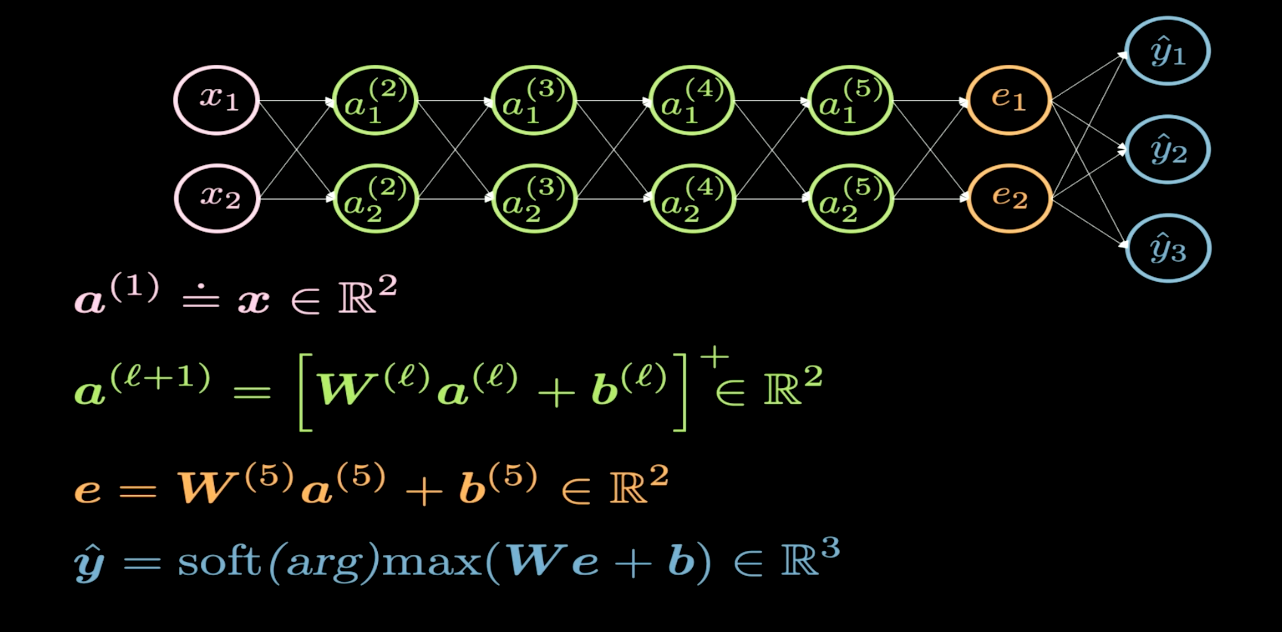
図1: ネットワーク構造

図1は、可視化するニューラルネットワークの構造を示しています。一般的に、ニューラルネットワークを描くときには、入力を下側または左側に、出力を上側または右側に描きます。図1では、ピンク色のニューロンが入力を表し、青色のニューロンが出力を表しています。このネットワークでは4つの隠れ層（緑の部分）があり、合計6層（4つの隠れ層＋1つの入力層＋1つの出力層）で構成されています。この例では隠れ層ごとに2つのニューロンがあるので、各層の重み行列($W$)の次元は2×2になります。これによって入力平面を可視化しやすい別の平面に変換しています。

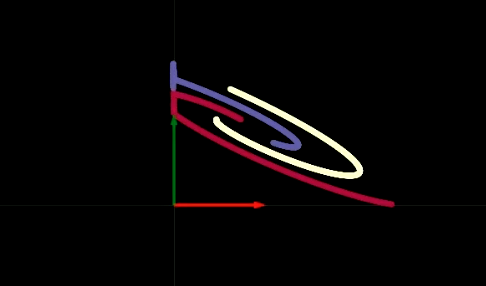
図2: folding spaceの可視化

各層での変換は、図2のように、ある特定の領域ごとに平面を折りたたむようなことに対応します。これは、すべての変換が2次元で行われているためです。実験から、各隠れ層に2つのニューロンしかない場合には最適化により時間がかかり、より多くのニューロンがあると最適化がより簡単であることがわかりました。このことは検討すべき重要な問題を提起します。隠れ層のニューロン数が少ないと、なぜネットワークを訓練するのが難しいのでしょうか？この問題はあなた自身で考えるべきであり、次の$\texttt{ReLU}$の可視化の後でもう一度この問題に立ち返ります。

(a)	(b)

ネットワークの隠れ層を1層ずつ進んでいくと、各層でアフィン変換が行われ、その後に非線形のReLU演算が適用されることで、負の値が除去されていくことがわかります。図3(a)と(b)に、ReLU演算子の可視化の結果を示します。ReLU演算子は非線形変換を行うのに役立ちます。ReLU演算子をともなったアフィン変換を何度も実行することによって、最終的には図4に示すように、データを線形分離することができます。

図4: 出力の可視化

この結果は、2つのニューロンからなる隠れ層が訓練しにくい理由についての、いくつかの洞察を与えてくれます。この6層ネットワークは、各隠れ層ごとに1つのバイアスを持っています。したがって、これらのバイアスのうちの1つが右上の象限から点を移動させた場合、その点の値はReLU演算子によってゼロになります。値が一度ゼロになると、後の層がどのようにデータを変換しても、値はゼロのままです。ニューラルネットワークを「太く」する - 具体的には隠れ層により多くのニューロンを追加する - あるいはより多くの隠れ層を追加するか、またはその両方を行うことによって - 訓練しやすくすることができます。このコースでは、与えられた問題に対して最適なネットワークアーキテクチャを決定する方法を探っていきます。

パラーメータ変換

一般的なパラメータ変換とは、パラメータベクトル$w$が関数の出力であることを意味します。この変換によって、元のパラメータ空間を別の空間に写すことができます。図5で$w$はパラメータ$u$を持つ$H$の出力であり、$G(x,w)$はネットワーク関数、$C(y,\bar y)$はコスト関数となります。この時、バックプロパゲーションは以下のように適用することができます。

これらの式は行列演算として適用されます。なお、各項の次元は一致している必要があります。$u$,$w$,$\frac{\partial H}{\partial u}^\top$,$\frac{\partial C}{\partial w}^\top$の次元は、それぞれ、$[N_u \times 1]$,$[N_w \times 1]$,$[N_u \times N_w]$,$[N_w \times 1]$,$[N_w \times 1]$となります。したがって、バックプロパゲーションの次元は一致していることになります。

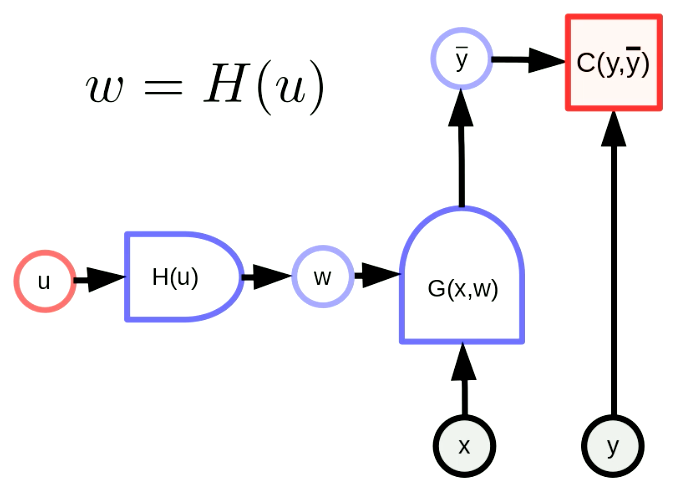
図5 一般的なパラメータ変換の形式

シンプルなパラメータ変換: 重み共有

重み共有変換とは、単一の$u$に由来する$H(u)$を、複数の$w$に複製することを意味します。つまり$H(u)$は、$u_1$を$w_1$, $w_2$へと複製するY字型分岐のようなものとなり、次のように表すことができます。

共有パラメーターが等しくなるように強制するため、共有されたパラメータの勾配はバックプロパゲーション時に足し合わされます。たとえば、$u_1$に関するコスト関数$C(y, \bar y)$の勾配は、$w_1$に関するコスト関数$C(y, \bar y)$の勾配と、$w_2$に関するコスト関数$C(y, \bar y)$の勾配との合計となります。

ハイパーネットワーク

ハイパーネットワークとは、あるネットワークの重みが別のネットワークの出力であるネットワークのことです。図6は「ハイパーネットワーク」の計算グラフを示しています。ここで関数$H$は、パラメータベクトル$u$と入力$x$を持つネットワークとなっており、$G(x,w)$の重みは、ネットワーク$H(x,u)$によって動的に設定されます。ハイパーネットワークは古くからある考え方ですが、今でも非常に強力な方法であることに変わりはありません。

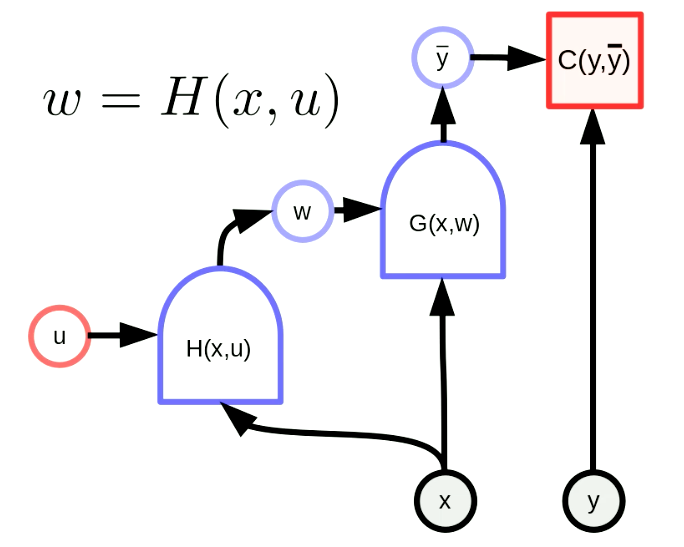
図6: 「ハイパーネットワーク」の構造

連続したデータにおけるモチーフ検出

重み共有変換はモチーフ検出に応用することができます。モチーフ検出とは、音声やテキストのキーワードのように、連続したデータの中からいくつかのモチーフを見つけることを意味します。これを実現する方法の一つとして、図7に示すように、データ上で移動窓を使用して、特定のモチーフ(例えば、音声信号中の特定の音)を検出するために重み共有関数を移動させ、その出力(例えば、スコア)をmax関数によって統合します。

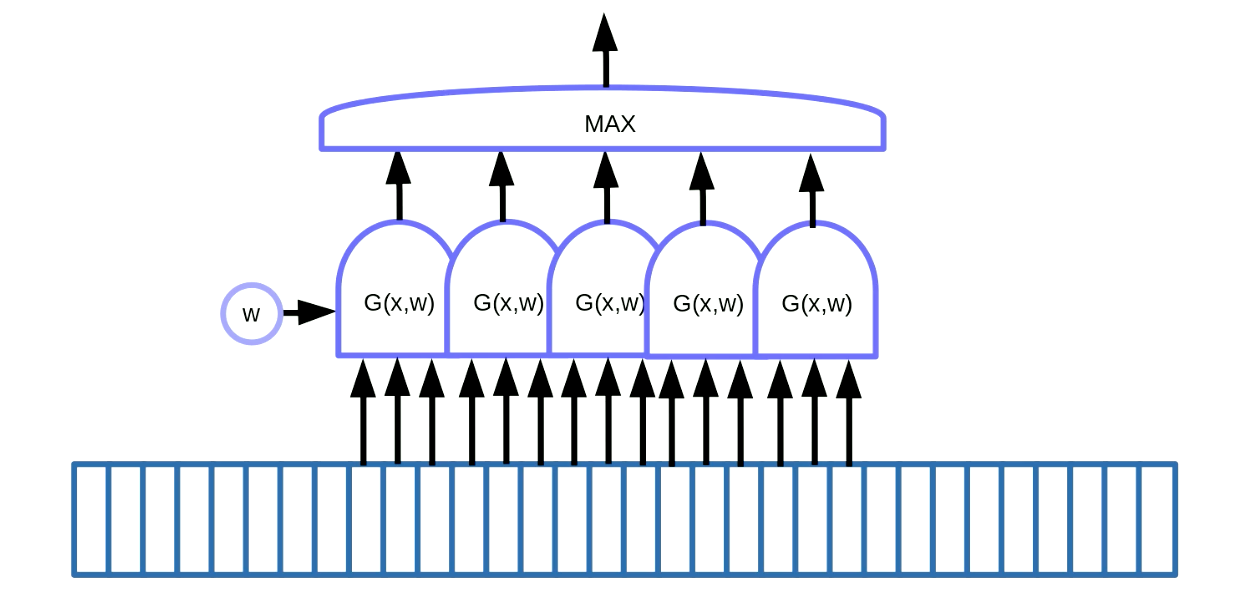
図7: 連続したデータでのモチーフ検出

図7の例では5つの重み共有関数を用意しています。この解決策の結果、5つの勾配を合計し、誤差を逆伝播させてパラメータ$w$を更新しています。PyTorchでこれを実装するには、これらの勾配が暗黙のうちに足し合わされるのを防ぐため、zero_grad()を使って勾配を初期化する必要があります。

画像におけるモチーフ検出

もう一つの応用は画像におけるモチーフ検出です。私たちは通常、画像上で「テンプレート」を走査することによって、位置や形の歪みの影響を受けない形の検出を行っています。簡単な例として「C」と「D」を区別を見てみましょう(図8)。「C」と「D」の違いは、「C」には2つの端点があり、「D」には2つの角があることです。そこで、「端点テンプレート」と「角テンプレート」を設計します。「テンプレート」と似たような形状であれば、閾値を超えた出力を持つことになります。そして、これらの出力を合計することで、「C」と「D」を区別することができます。図8では、ネットワークが2つの端点と0つの角を検出しているので、「C」が活性化されています。

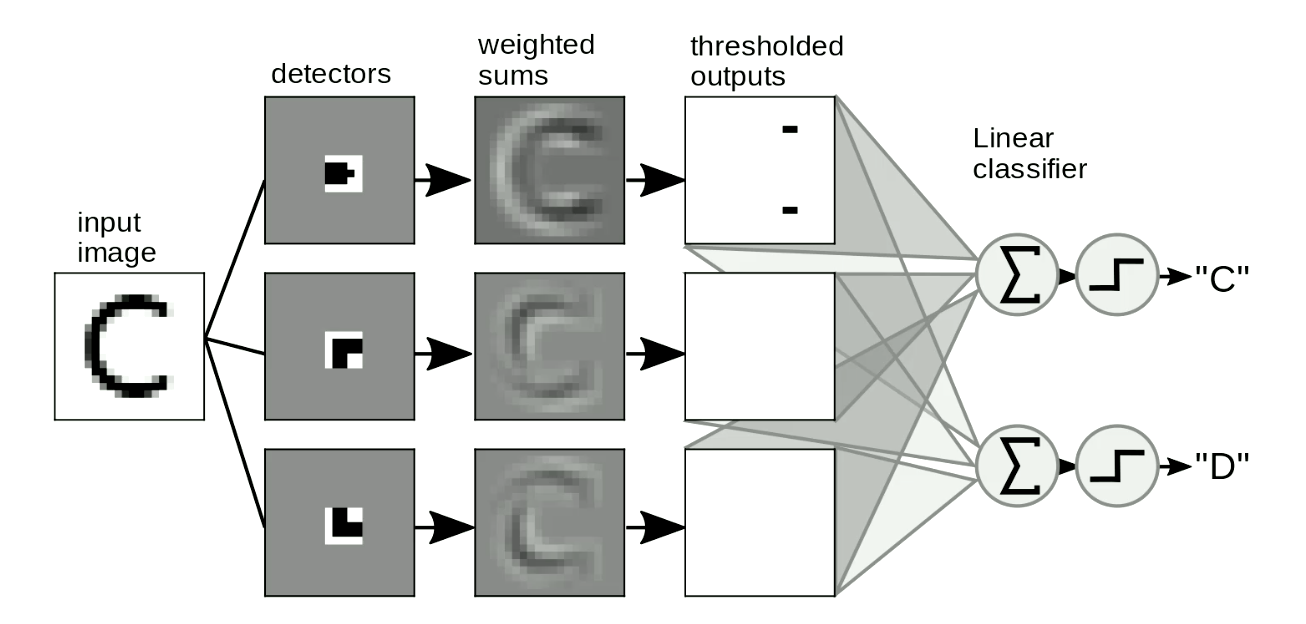
図8: 画像でのモチーフ検出

また、このような「テンプレートマッチング」がシフト不変であることも重要です - 入力をシフトさせても、出力（検出された文字）は変化しません。これは、重み共有変換で解決できます。図9に示すように、「D」の位置を変えても、位置のシフトした角のモチーフを検出することができます。モチーフを合計するとによって、「D」を検出することができます。

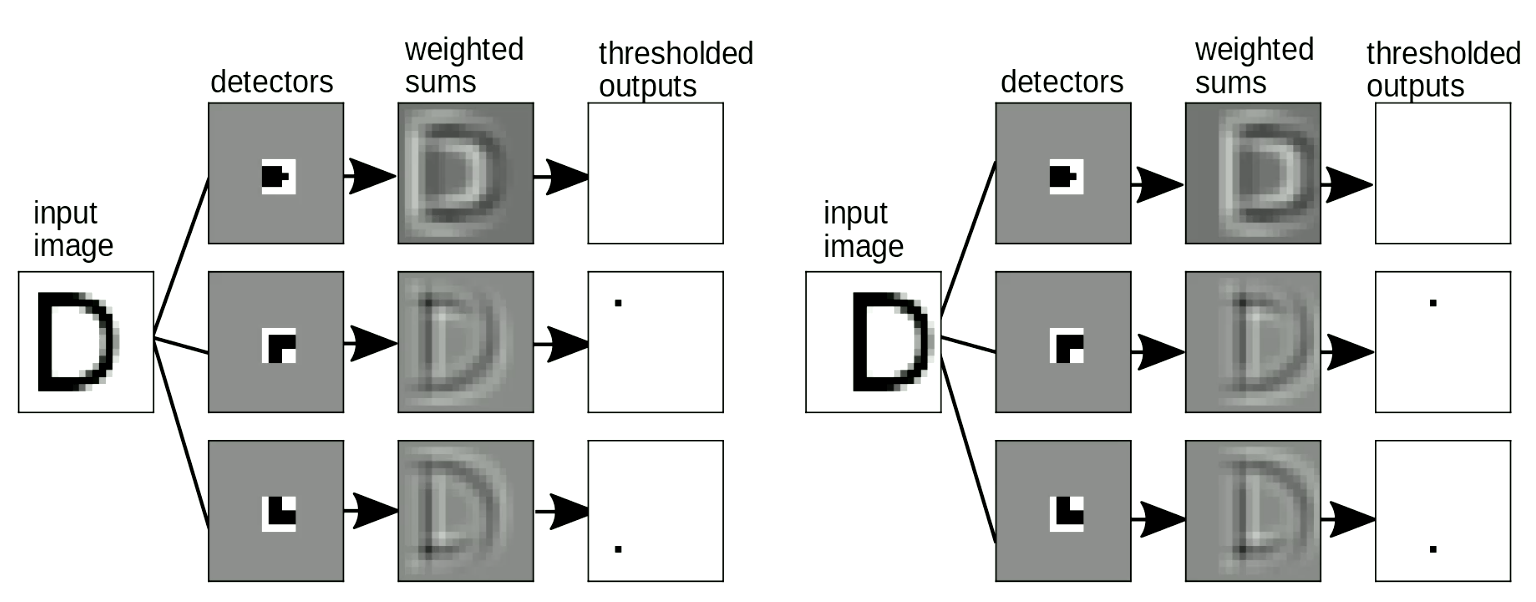
図9: シフト不変

局所的な検出器と総和を用いた「hand-crafted」な方法による認識は長年使われてきましたが、同時に次のような問題を提起します。このような「テンプレート」を自動的にデザインすることは可能でしょうか？我々はニューラルネットワークを用いてこのような「テンプレート」を学習させることができるでしょうか？次の節では、畳み込みという概念を導入することによって、画像に「テンプレート」を適用する方法を紹介します。

離散的畳み込み

畳み込み

入力$x$と$w$との1次元の畳み込みの正確な数学的定義は次のようになります。

ここで$i$番目の出力は、逆順の$w$と、$w$と同じサイズの窓で切り出された$x$とのドット積として計算されます。すべての出力を計算するためには、窓を先頭から開始して1つずつシフトしてゆき、$x$がなくなるまで繰り返します。

相互相関

実際には、PyTorchなどのディープラーニングのフレームワークで採用されている慣習は少し異なります。PyTorchの畳み込みは、$w$が逆順とならない形で実装されています。

数学者はこの定式化を「相互相関」と呼びますが、我々の文脈では，この違いは単なる慣習の違いに過ぎません。実際には、メモリに格納されている重みを前から読むか、後ろから読むかで、相互相関と畳み込みは交換可能です。

この違いを意識することは、例えば、数学のテキストから、畳み込み/相関の、ある数学的性質を利用したい場合などに重要となります。

高次元の畳み込み

画像のような2次元の入力に対しては，2次元での畳み込みを利用します。

この定義は、2次元以上の3次元や4次元に簡単に拡張することができます。ここでは$w$を畳み込みカーネルと呼びます。

DCNNにおける畳み込み演算でよく用いられる特殊なパラメータ

1. ストライド: $x$内のウィンドウを一度に1エントリずつ移動するのではなく、より大きなステップで移動させます(例えば、一度に2エントリや3エントリを移動します)。 例: 入力$x$が一次元でサイズが100、$w$のサイズが5であるとします。ストライドが1または2の場合の出力サイズは、下の表のようになります。

1. パディング: ディープニューラルネットワークのアーキテクチャを設計する際には、畳み込みの出力を入力と同じサイズにしたいことがよくあります。これは、入力の両端に(通常は)ゼロのエントリをいくつか(通常は両側に)パディングすることで実現できます。パディングは主に利便性のために行われます。これはしばしばパフォーマンスに影響を与え、奇妙な境界効果をもたらすことがありますが、ReLUの非線形性を利用する場合、ゼロパディングは不合理ではありません。

Deep Convolution Neural Networks (DCNNs)

前述のように、ディープニューラルネットワークは、典型的には、線形演算の層と要素ごとの非線形演算の層を交互に繰り返されるように構成されています。畳み込みニューラルネットワークでは、線形演算は上述の畳み込み演算となります。また、プーリング層と呼ばれる第３のタイプの層も存在します。

このような層を複数重ねる理由は、データの階層的な表現を構築したいからです。CNNは画像の処理のみだけではなく、音声や言語への応用にも成功しています。技術的には、配列で表すことのできるあらゆるタイプのデータに適用できますが、これらの配列は特定の性質を満たす必要があります。

なぜ私たちは世界の階層的な表現を獲得したいのでしょうか？それは、私たちが住んでいる世界は構成的だからです。この点については、前のセクションでも触れました。このような階層的な性質は、局所的なピクセルが集まって特定の方向を持つエッジのような単純なモチーフを形成していることなどからも観察することができます。これらのエッジは、コーナーやT字路などの局所的な特徴を形成するために組み合わされます。また、これらのエッジは、より抽象的なモチーフを形成するために組み合わされます。このような階層的な表現を積み重ねることで、最終的には実世界で観測される物体を形成することができるのです。

図10: ImageNetで学習された畳み込みネットワークの特徴の可視化 [Zeiler & Fergus 2013]

私たちが自然界で観察するこの構成的、階層的な性質は、単に私たちの視覚的な知覚の結果ではなく、物理的なレベルでも当てはまります。最も低いレベルの記述では、原子を形成するために集まった素粒子があり、原子が一緒になって分子を形成して、このようなプロセスを繰り返す事によって、物質や物体の一部、そして最終的には完全な物体を形成されます。

世界の構成的性質は、人間が自分たちが住んでいる世界をどのように理解しているかについてのEinsteinの修辞的な質問への答えになるかもしれません。

宇宙について最も理解できないことは、それが理解可能であるということである。

人間がこの構成性のおかげで世界を理解しているという事実は、陰謀のようにも思えてしまいます。しかし、構成性がなければ、人間が自分たちの住んでいる世界を理解するには、さらに魔法が必要になるとも言われています。以下に偉大な数学者Stuart Gemanの言葉を引用します。

世界は構成的であるか、神が存在するかのどちらかである。

生物からのヒント

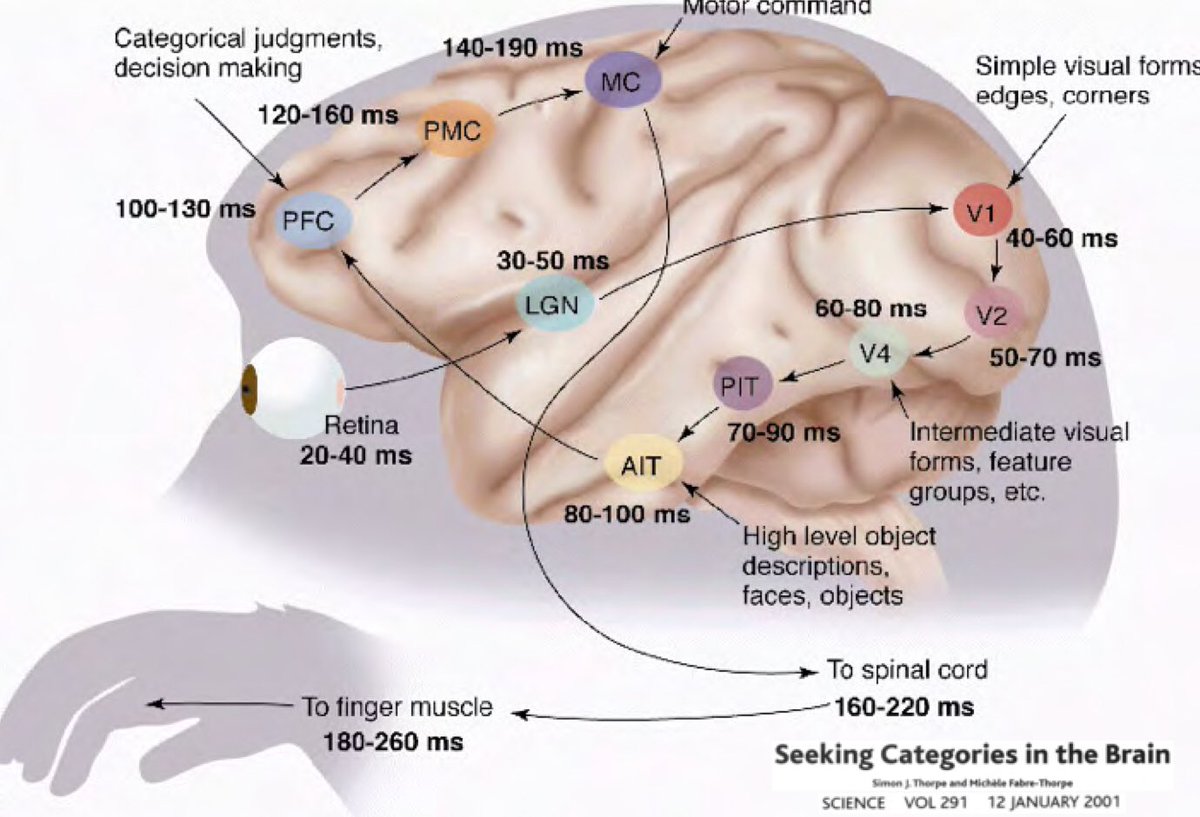
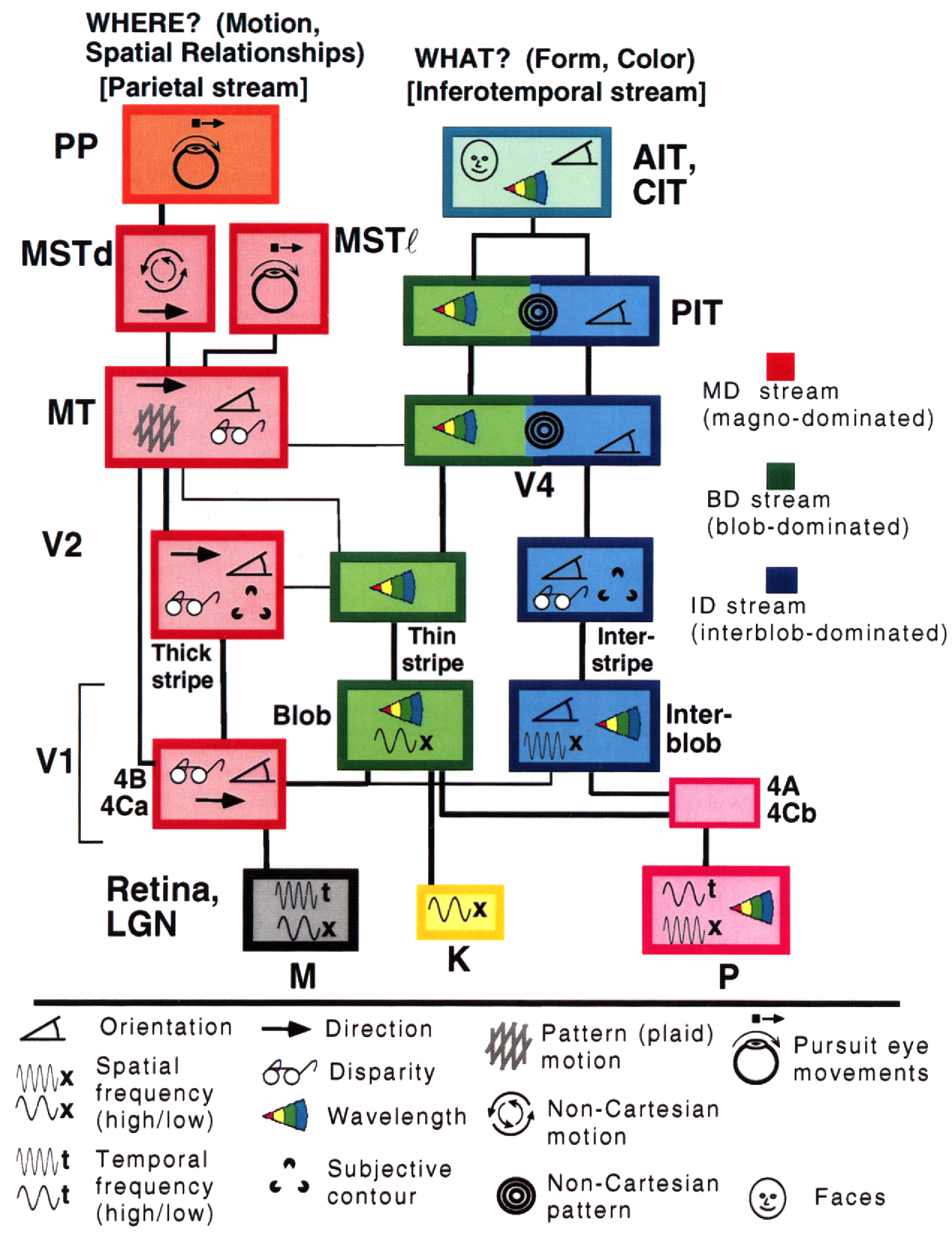
なぜディープラーニングは、私たちの世界は理解可能であり、構成的な性質を持っているという考えに根ざしたものでなければならないのでしょうか？Simon Thorpeが行った研究は、このような考えをさらに推し進めることに役立ちます。Thropeは、私たちが日常的な物体を認識する方法が非常に高速であることを示しました。実験で、100ミリ秒ごとに一組の画像を点滅させ、被験者に画像を識別してもらったところ、きちんと識別できることがわかりました。これは人間が物体を検出するのに約100ミリ秒かかることを示しています。下の図は、目から入った信号が脳の各部位をどのくらいの時間で伝わっているかを示したものです。

図11: Simon Thorpeの脳における視覚情報処理のモデル

信号は、網膜から外側膝状体(lateral geniculate body (LGN), コントラスト強調やゲート制御を行っています)を経て、第1次視覚野(V1)、さらにV2、V4を通って、側頭皮質(PIT)とよばれる物体の種類を分類する脳部位に伝わっていきます。直視下脳手術における実験から、PITのニューロンは特定の画像、例えば有名な女優や被験者のおばあちゃんを見せられたときにのみ発火し、それ以外は発火しないことが知られています。このようなニューロンの活動は、対象の位置や、大きさ、照明、おばあちゃんの向きや服装などに左右されません。 さらに、人間がこれらの対象を識別するための反応時間(数本のスパイクが通過するのにやっとな時間)は、複雑な再帰的計算に余計な時間を費やすことなく、このような識別が可能であることを示しています。つまり、単一のフィードフォワード処理で行われていると考えられます。 これらの洞察は、完全にフィードフォワードでありながらも、識別に無関係な変換に影響されずに認識課題を解決できるニューラルネットワークのアーキテクチャを開発できることを示唆しています。 人間の脳からのさらなる洞察は、GallantとVan Essenによるもので、彼らのモデルは人間の脳が2つの分離した経路を持つことを示しています。

図12: GallantとVan Essenによる脳の背側およびに腹側経路のモデル

図12の右側は何を見ているかを伝える腹側経路を示し、左側は位置、形状、運動を識別する背側経路を示しています。これらは人間(と霊長類)の視覚野ではかなり分離されていると考えられています(もちろん、多少の相互作用はあります)。 ### HubelとWeiselによる研究 (1962)

図13: HubelとWeiselによる猫の脳における視覚実験

HubelとWeiselは、電極を使って、視覚刺激に対応する猫の脳内の神経発火を測定しました。彼らは、V1領域のニューロンは、視野の特定の領域(「受容野」と呼ばれます)だけに反応し、その領域の特定の方向のエッジを検出することを発見しました。例えば、猫に回転する真っ直ぐな棒を見せると、特定の角度の時にニューロンが発火し、特定の角度から遠ざかるにつれて、活動が減少することを確認しました。これらの特徴選択的に活動するニューロンを、HubelとWeiselは、局所的な特徴を検出することから「単純細胞」と名付けました。 また彼らは、ある特徴選択的なニューロンは、棒を受容野の外に移動させると発火しなくなりますが、今度は別のニューロンが発火することを発見しました。視野全体にこのような局所的な特徴検出器がまんべんなく存在することから、人間の脳は視覚情報を「畳み込み」の集合体として処理していると考えることができます。 もう一つのタイプのニューロンは、彼らが「複雑細胞」と名付けたもので、ある領域内の複数の単純細胞の出力を集約します。これは、最大値、総和、二乗和などの関数や、順序に依存しないその他の関数を使って、活動の集合を計算していると考えることができます。これらの複雑細胞は、領域内のどこに刺激があるかに関係なく、領域内のエッジや方位を検出します。これは、入力の位置のわずかな変化に対してシフト不変であると言い換えることができます。 ### 福島による研究 (1982)

図14: 福島のCNNモデル

福島は1982年に、単純細胞と複雑細胞によっての構成された多層の畳み込みニューラルネットワークのモデルを世界で初めて実装し、手書き数字のデータセットに適用しました。ネットワークの特徴検出器はhand-craftedであるか、もしくは学習によって獲得されるものとなっていましたが、学習にバックプロパゲーションはまだ用いられておらず、教師なしのクラスタリングアルゴリズムによって各層ごとに別々に学習していました。 数年後（1989、1998年）に Yann LeCun が、同様のアーキテクチャを実装し、バックプロパゲーションを用いて教師ありの設定での学習を実現しました。一般的にはこれが現代の畳み込みニューラルネットワークの起源とみなされています。(注: 1999年にMITのRiesenhuberもこのアーキテクチャを再発見しましたが、彼はバックプロパゲーションを使用していませんでした)。