人工ニューラルネットワーク(ANN)

🎙️ Alfredo Canziani

分類のための教師あり学習

• 下の 図1(a) を考えてみましょう。このグラフの点は、螺旋の枝の上にあり、$\R^2$の中にいます。それぞれの色はクラスのラベルを表しています。一意なクラスの数は $K = 3$ です。これは、数学的には、式1(a) で表されます。

• 図1(b) は、ガウスノイズ項を加えた、同様の螺旋を示しています。これは数学的には 式1(b) で表されます。

  どちらの場合も、これらの点は線形分離不可能です。

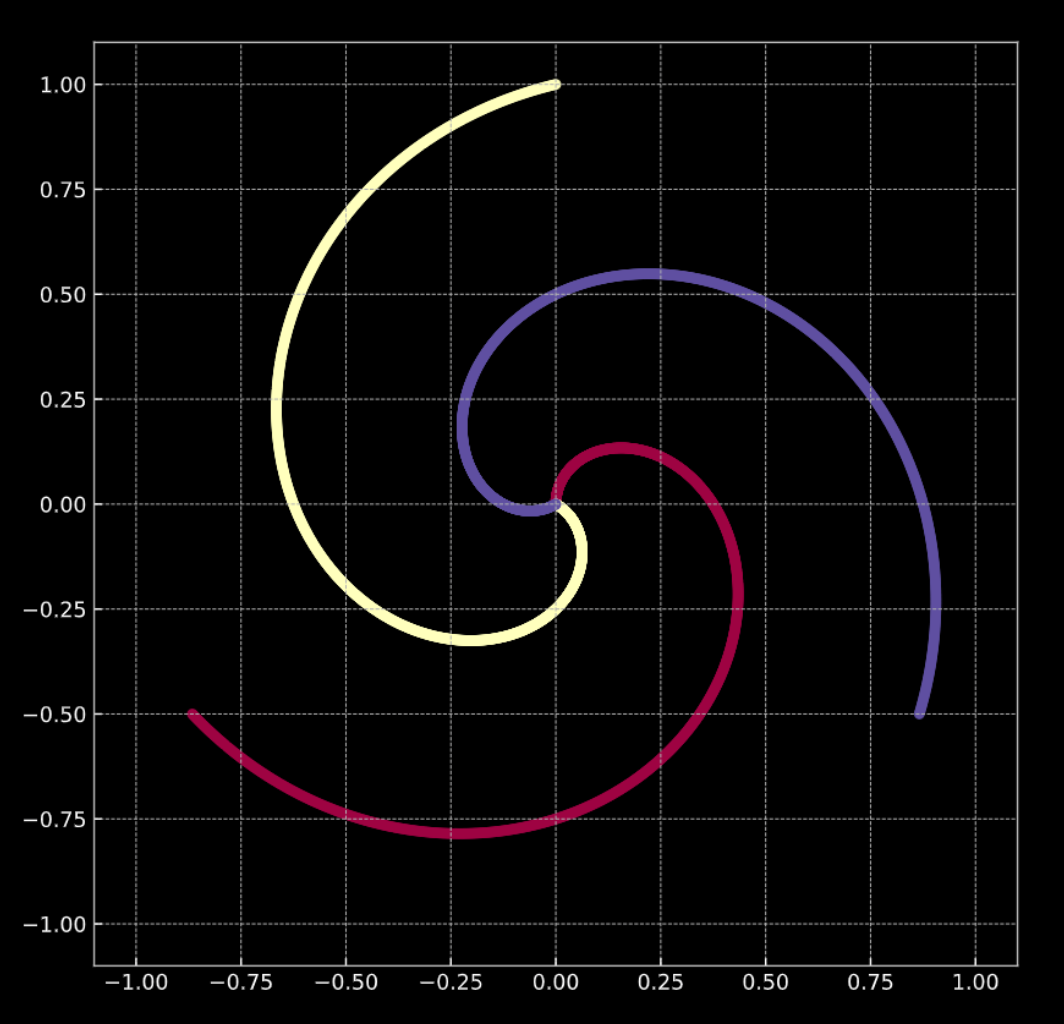
  図1(a) 「ノイズがない」２次元螺旋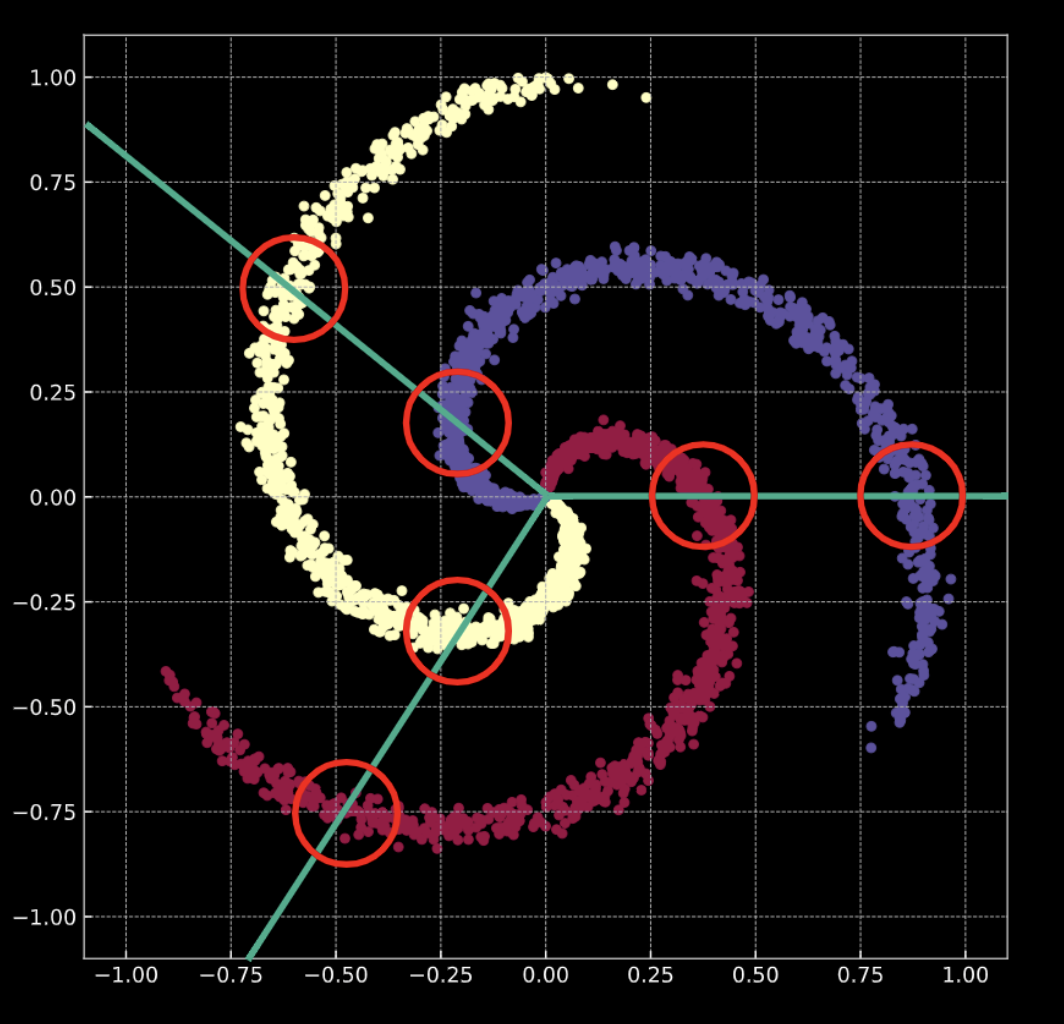

  図1(b) 「ノイズがある」２次元螺旋

\[X_{k}(t)=t\left(\begin{array}{c}{\sin \left[\frac{2 \pi}{K}(2 t+k-1)\right]} \\ {\cos \left[\frac{2 \pi}{K}(2 t+k-1)\right]}\end{array}\right) \\ 0 \leq t \leq 1, \quad k=1, ..., K\]

式1(a) \[X_{k}(t)=t\left(\begin{array}{c}{\sin \left[\frac{2 \pi}{K}(2 t+k-1 +\mathcal{N}\left(0, \sigma^{2}\right))\right]} \\ {\cos \left[\frac{2 \pi}{K}(2 t+k-1 +\mathcal{N}\left(0, \sigma^{2}\right))\right]}\end{array}\right)\\0 \leq t \leq 1, \quad k=1, ..., K\] 式1(b)

分類を行うとはどういうことでしょうか？ ロジスティック回帰の場合を考えてみましょう。分類のためのロジスティック回帰がこのデータに適用された場合、データをそのクラスに分離しようとして、線形平面（決定境界）の集合を作成します。この解決策の問題点は、各領域に複数のクラスに属する点があることです。螺旋の枝は線形決定境界を横切っています。これは、優れた解決策ではありません!

どうやってこれを解決するのでしょうか？ 入力空間を線形分離可能になるように変換します。これを行うためにニューラルネットワークを訓練する過程で、ニューラルネットワークが学習する決定境界は訓練データの分布に適応しようとします。

注：この講義では、ニューラルネットワークは常に入力に近い層から順に下から上に表現されます。最初の層が一番下にあり、最後の層が一番上にあります。これは、概念的には、入力データはニューラルネットワークが試みようとしているタスクのための低次の特徴だからです。データがネットワークを通って上向きに移動すると、後続の各層はより高次の特徴を抽出します。

訓練データ

先週、新しく初期化されたニューラルネットワークが入力を任意の方法で変換することを見ました。しかし、この変換は、目下のタスクを実行するのに (最初は) 役に立ちません。データを使用して、どのようにしてこの変換を強制的に、目下のタスクに関連する何らかの意味を持たせることができるかを探ります。以下は、ネットワークの訓練の入力として使用されるデータです。

• $\vect{X}$は入力データを表現しています。これは$m$ (訓練データ点の数) x $n$ (各入力点の次元)の行列です。図1(a)、1(b) のデータの場合、$n = 2$です。

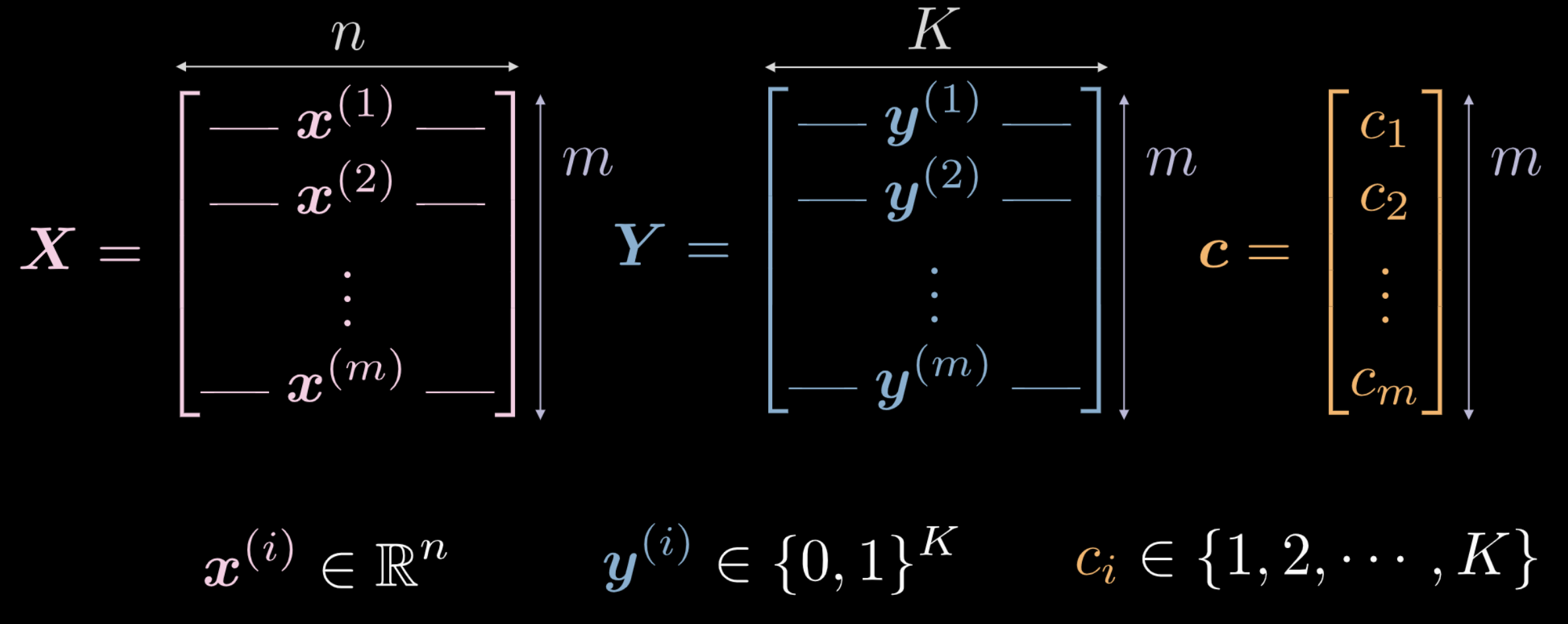
図2 訓練データ

• ベクトル $\vect{c}$ と行列 $\boldsymbol{Y}$ は、それぞれの $m$ データ点のクラスラベルを表しています。上の例では、$3$ 個のクラスがあります。

  • $c_i \in \lbrace 1, 2, \cdots, K \rbrace$, そして $\vect{c} \in \R^m$です。 ただし、訓練データとして $\vect{c}$ を使用しない場合もあります。また、クラスラベルを異なる数値ラベル$c_i \in \lbrace 1, 2, \cdots, K \rbrace$にしてしまうと、クラス内での順序を推測してしまい、データの分布とは異なるものになってしまう可能性があります。
  • この問題を回避するために、one-hot符号化を使用します。各ラベル$c_i$に対して、$K$次元のゼロベクトル$\vect{y}^{(i)}$を作成し、$c_i$番目の要素を$1$とします(下図の図3参照)。

図3 one-hot符号化

• よって、$\boldsymbol Y \in \R^{m \times K}$です。この行列は、\(K\)の一つの点に完全に集中しているある確率質量を持っていると考えることもできます。

全結合層

ここでは、全結合（FC）ネットワークとは何か、その仕組みを見ていきましょう。

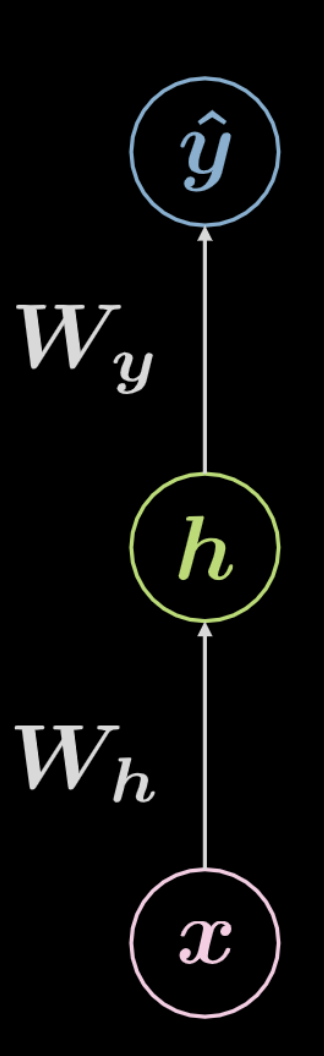
図4 全結合ニューラルネットワーク

図4 のネットワークを考えてみましょう。入力データである$\boldsymbol x$には、$\boldsymbol W_h$で定義されたアフィン変換が行われ、その後、非線形変換が行われます。この非線形変換の結果を $\boldsymbol h$ と呼びます。これは隠れ層の出力、つまりネットワークの外から見ることのできない出力を表しています。これに対して、別のアフィン変換（$\boldsymbol W_y$）に続いて、別の非線形変換が行われます。これが最終的な出力である$\boldsymbol{\hat{y}}$ を生成します。このネットワークは、以下の 式2 で数学的に表すことができます。ここで、$f$と$g$はともに非線形活性化関数です。

\[\begin{aligned} &\boldsymbol h=f\left(\boldsymbol{W}_{h} \boldsymbol x+ \boldsymbol b_{h}\right)\\ &\boldsymbol{\hat{y}}=g\left(\boldsymbol{W}_{y} \boldsymbol h+ \boldsymbol b_{y}\right) \end{aligned}\] 式2 FCネットワークの背後にある数学

上記のような基本的なニューラルネットワークは、単に連続したペアの集合であり、各ペアではアフィン変換に続いて非線形演算（スカッシング）が行われます。よく使われる非線形関数には、ReLU、シグモイド、tanh、ソフトマックスなどがあります。

上図のネットワークは3層のネットワークです。

1. 入力ニューロン
2. 隠れニューロン
3. 出力ニューロン

したがって、$3$層のニューラルネットワークは、$2$つのアフィン変換を持っています。これは、$n$層のネットワークに一般化することができます。

では、もっと複雑なケースに移りましょう。

3つの隠れ層があり、各層が全結合である場合を考えてみましょう。図は、図5にあります。

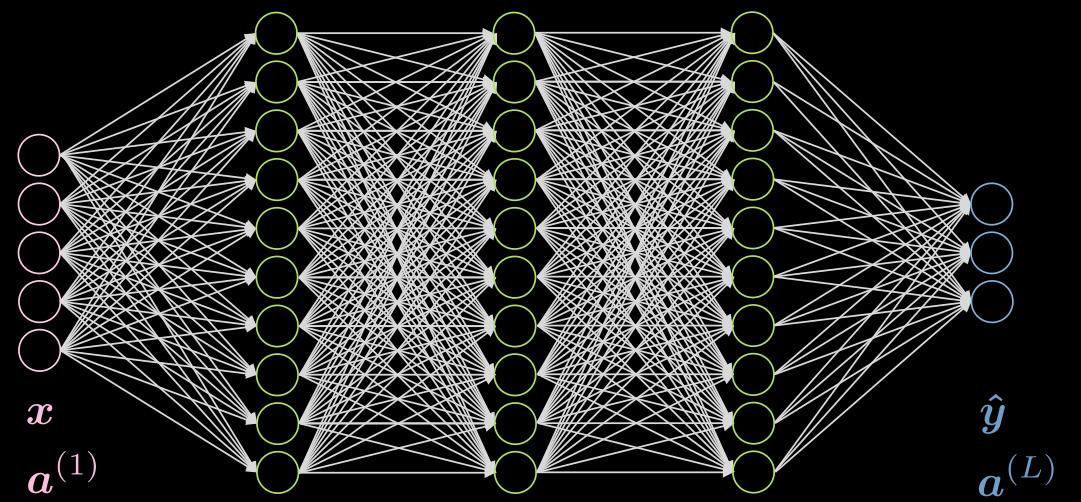
図5 三層の隠れ層を持つニューラルネット

第二層のニューロン $j$ を考えてみましょう。そのactivationは

\[a^{(2)}_j = f(\boldsymbol w^{(j)} \boldsymbol x + b_j) = f\Big( \big(\sum_{i=1}^n w_i^{(j)} x_i\big) +b_j ) \Big)\]

となります。ただし、$\vect{w}^{(j)}$は$\vect{W}^{(1)}$の$j$行目です。

この場合の入力層のactivationは、単なる恒等写像であることに注意してください。隠れ層は、ReLU、tanh、シグモイド、ソフト(arg)maxなどの活性化関数を持つことができます。

一般的に最後の層の活性化関数は、この Piazzaの投稿で説明されているように、使用ケースに依存します。

ニューラルネットワーク (推論)

図6にあるような3層（入力、隠れ、出力）のニューラルネットワークについてもう一度考えてみましょう。

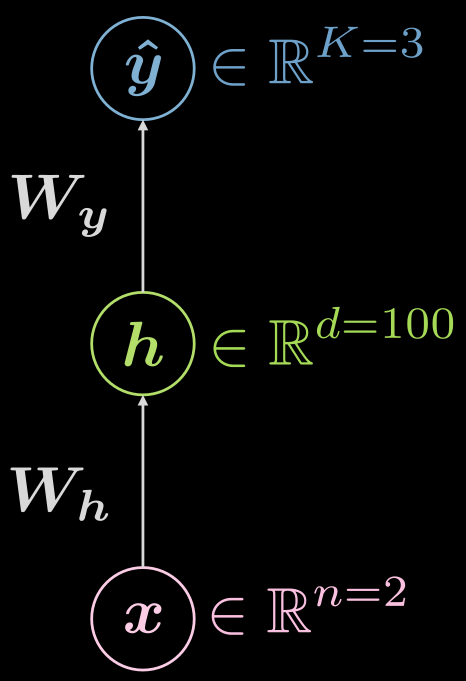
図6 三層ニューラルネットワーク

どんな関数を見ているのでしょうか？

\[\boldsymbol {\hat{y}} = \boldsymbol{\hat{y}(x)}, \boldsymbol{\hat{y}}: \mathbb{R}^n \rightarrow \mathbb{R}^K, \boldsymbol{x} \mapsto \boldsymbol{\hat{y}}\]

ただし、隠れ層があることを可視化しておくと便利で、写像を次のように展開することができます。

\[\boldsymbol{\hat{y}}: \mathbb{R}^{n} \rightarrow \mathbb{R}^d \rightarrow \mathbb{R}^K, d \gg n, K\]

上記の場合の設定例は、どのように見えるでしょうか？この場合、2次元の入力があり($n=2$)、1つの隠れ層の次元数は1000($d = 1000$)で、3つのクラスがあります($C=3$)。1つの隠れ層にそれほど多くのニューロンを入れたくないという実用的な理由があるので、その1つの隠れ層を10個ずつのニューロンで3つに分割するのは理にかなっているかもしれません ($1000 \rightarrow 10 \times 10 \times 10$)。

ニューラルネットワーク (訓練I)

では、典型的な訓練とはどのようなものなのでしょうか？これを損失の標準的な用語に定式化しておくと便利です。

まず、soft(arg)maxを再導入します。そして、この活性化関数は、多クラス予測のために負の対数尤度損失を使う場合、最後の層に用いられる一般的な活性化関数であることを明示しておきましょう。LeCun教授が講義で述べているように、これは、シグモイドや二乗損失を使用する場合よりも良い勾配を得ることができるからです。さらに、この活性化関数を使うことで、最後の層はすでに正規化された状態になります(最後の層のすべてのニューロンの和が1になります)が、これは明示的な正規化(ノルムで割る)よりも勾配法に適しています。

soft (arg)maxを使うと、最後の層のロジットは次のようになります。

\(\text{soft{(arg)}max}(\boldsymbol{l})[c] = \frac{ \exp(\boldsymbol{l}[c])} {\sum^K_{k=1} \exp(\boldsymbol{l}[k])} \in (0, 1)\) <!– It is important to note that the set is not closed because of the strictly positive nature of the exponential function.

Given the set of the predictions $\matr{\hat{Y}}$, the loss will be: –>

指数関数は厳密に正であるという性質を持つため、集合は閉じていないことに注意してください。

予測値の集合が $\matr{\hat{Y}}$ であるとすると、損失は次のようになります。

\[\mathcal{L}(\boldsymbol{\hat{Y}}, \boldsymbol{c}) = \frac{1}{m} \sum_{i=1}^m \ell(\boldsymbol{\hat{y}_i}, c_i), \quad \ell(\boldsymbol{\hat{y}}, c) = -\log(\boldsymbol{\hat{y}}[c])\]

ここで $c$ は整数のラベルを表し、one-hot符号化の表現ではありません。

そこで、あるサンプルが正しく分類されている場合とそうでない場合の 2 つの例をやってみましょう。

以下のようにしましょう。

\[\boldsymbol{x}, c = 1 \Rightarrow \boldsymbol{y} = {\footnotesize\begin{pmatrix} 1 \\ 0 \\ 0 \end{pmatrix}}\]

インスタンスごとの損失はどうなるでしょうka ？

ほぼ完璧な予測の場合には、（$\sim$ は おおよそ の意味）

\[\hat{\boldsymbol{y}}(\boldsymbol{x}) = {\footnotesize\begin{pmatrix} \sim 1 \\ \sim 0 \\ \sim 0 \end{pmatrix}} \Rightarrow \ell \left( {\footnotesize\begin{pmatrix} \sim 1 \\ \sim 0 \\ \sim 0 \end{pmatrix}} , 1\right) \rightarrow 0^{+}\]

ほぼ絶対に間違っている場合には、

\[\hat{\boldsymbol{y}}(\boldsymbol{x}) = {\footnotesize\begin{pmatrix} \sim 0 \\ \sim 1 \\ \sim 0 \end{pmatrix}} \Rightarrow \ell \left( {\footnotesize\begin{pmatrix} \sim 0 \\ \sim 1 \\ \sim 0 \end{pmatrix}} , 1\right) \rightarrow +\infty\]

上の例では、$\sim 0 \rightarrow 0^{+}$ と $\sim 1 \rightarrow 1^{-}$ となっています。なぜでしょうか？ちょっと考えてみてください。

注 CrossEntropyLossを使うと、LogSoftMaxと負の対数尤度NLLLossが一緒になってしまうので、二度手間にならないようにしましょう。

ニューラルネットワーク（訓練II）

学習のためには、学習可能なパラメータ（重み行列とバイアス）を我々が$\mathbf{\Theta} = \lbrace\boldsymbol{W_h, b_h, W_y, b_y} \rbrace$と呼ぶものに集約します。これにより、目的関数や損失を次のように書くことができます。

\(J \left( \mathbf{\Theta} \right) = \mathcal{L} \left( \boldsymbol{\hat{Y}} \left( \mathbf{\Theta} \right), \boldsymbol c \right) \in \mathbb{R}^{+}\) <!– This makes the loss depend on the output of the network $\boldsymbol {\hat{Y}} \left( \mathbf{\Theta} \right)$, so we can turn this into an optimization problem.

A simple illustration of how this works can be seen in Fig. 7, where $J(\vartheta)$, the function we need to minimise, has only a scalar parameter $\vartheta$. –>

これにより、損失はネットワークの出力 $\boldsymbol {\hat{Y}} \left( \mathbf{\Theta} \right)$に依存することになるので、最適化問題にすることができます。

これがどのように動作するかの簡単な説明は、図7にあります。ここで、最小化する関数$J(\vartheta)$は、スカラーパラメータ$\vartheta$しか持ちません。

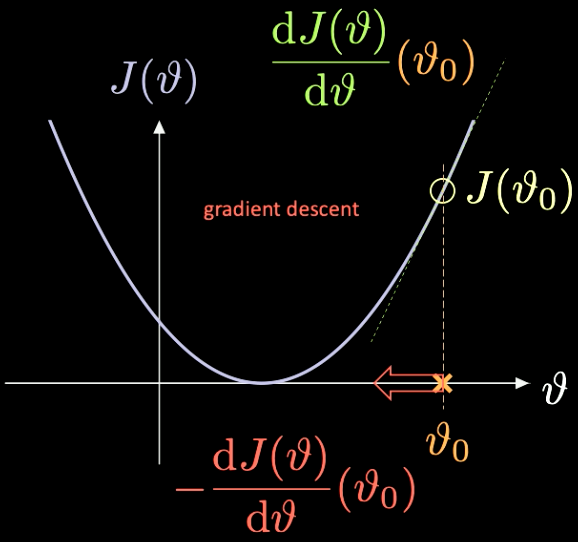
図7 勾配降下法による損失関数の最適化

ランダムな初期値$\vartheta_0$、そしてそれによって定まる損失$J(\vartheta_0)$を定めます。その点で評価された微分$J’(\vartheta_0) = \frac{\text{d} J(\vartheta)}{\text{d} \vartheta} (\vartheta_0)$を計算することができます。この場合、微分の傾きは正の値になります。ということで、急降下の方向に一歩踏み出す必要があります。この場合、それは $-\frac{\text{d} J(\vartheta)}{\text{d} \vartheta}(\vartheta_0)$です。

このプロセスを反復的に繰り返すことを 勾配降下法といいます。勾配法はニューラルネットワークを訓練するための主要な方法です。

必要な勾配を計算するためには、以下に示すような誤差逆伝播を用いなければなりません

\[\frac{\partial \, J(\mathbf{\Theta})}{\partial \, \boldsymbol{W_y}} = \frac{\partial \, J(\mathbf{\Theta})}{\partial \, \boldsymbol{\hat{y}}} \; \frac{\partial \, \boldsymbol{\hat{y}}}{\partial \, \boldsymbol{W_y}} \quad \quad \quad \frac{\partial \, J(\mathbf{\Theta})}{\partial \, \boldsymbol{W_h}} = \frac{\partial \, J(\mathbf{\Theta})}{\partial \, \boldsymbol{\hat{y}}} \; \frac{\partial \, \boldsymbol{\hat{y}}}{\partial \, \boldsymbol h} \;\frac{\partial \, \boldsymbol h}{\partial \, \boldsymbol{W_h}}\]

螺旋の分類 - Jupyter notebook

Jupyter notebookは ここ にあります。Notebookを実行するには、README.md で指定された dl-minicourse 環境がインストールされていることを確認してください。

torch.device() の使い方については、先週のノートに説明があります。

前回と同様に、$\mathbb{R}^2$の中の点を、赤、黄、青の3色のラベルで表現してみましょう。

図8 螺旋分類データ

nn.Sequential()は、追加された順にモジュールをコンストラクタに渡すコンテナですが、nn.linear() は、アフィン変換$\boldsymbol y = \boldsymbol W \boldsymbol x + \boldsymbol b$を適用するので、名前が間違っています。詳しくは PyTorchのドキュメント を参照してください。

アフィン変換とは、回転、反射、平行移動、スケーリング、剪断の5つであることを覚えておいてください。

図9にあるように、線形決定境界で螺旋データを分離しようとした場合、つまりnn.linear() モジュールのみを使用しそれらの間に非線形性を持たせな買った場合、最高の分類精度は50%です。

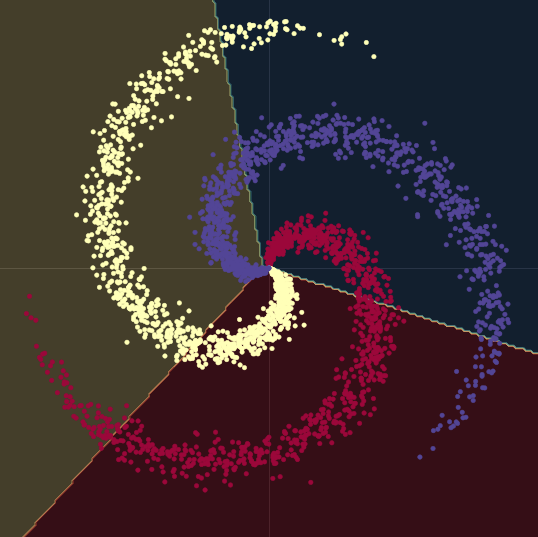
図9 線形決定境界

線形モデルから、2つの nn.linear() モジュールとその間の nn.ReLU() モジュールを持つモデルに移行すると、精度は95%まで上がります。これは、図10に示すように、境界線が非線形になり、データの螺旋状の形によく適応するからです。 <!–

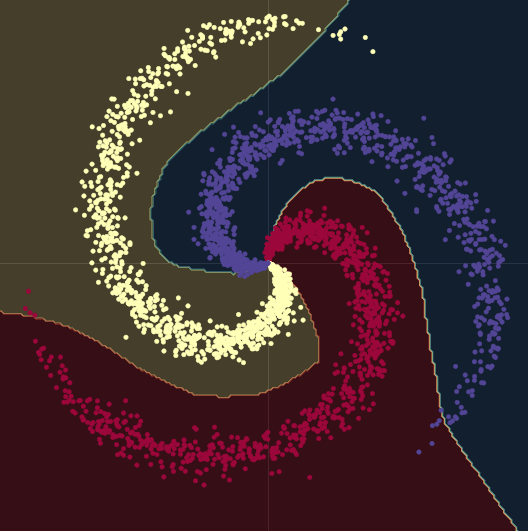
Fig. 10 Non-linear decision boundaries.

–>

図10 非線形決定境界

線形回帰では正しく解けないけれど、同じニューラルネットワーク構造では簡単に解ける回帰問題の例をこのnotebookと図11に示します。そこには、10の異なるネットワークが示されています。そのうち5つはnn.ReLU()を用いていて、残りの5つはnn.Tanh()を用いています。前者は断片的な線形関数であるのに対し、後者は連続的で滑らかな回帰です。

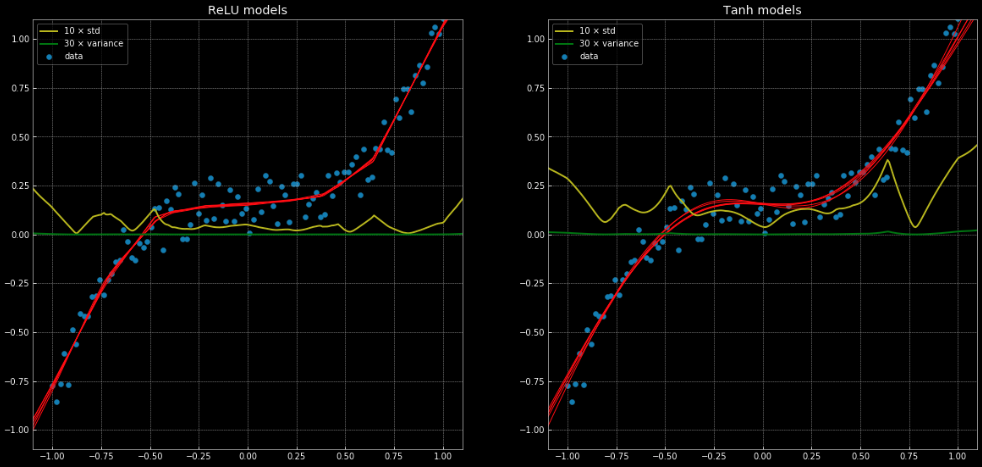
図11: 10個のニューラルネットとその分散と標準偏差
左: 5つの ReLU ネットワーク 右:　5つの tanh ネットワーク

黄色と緑の線は、ネットワークの標準偏差と分散を示しています。これらを使用することは、「信頼区間」のようなものに便利です。なぜなら、関数は出力ごとに単一の予測を与えるからです。アンサンブル分散予測を使用すると、予測が行われている不確実性を推定することができます。この重要性は、図12で見ることができます。ここでは、決定関数を訓練区間の外に拡張していますが、これらは$+\infty, -\infty$に向かっている傾向があります。

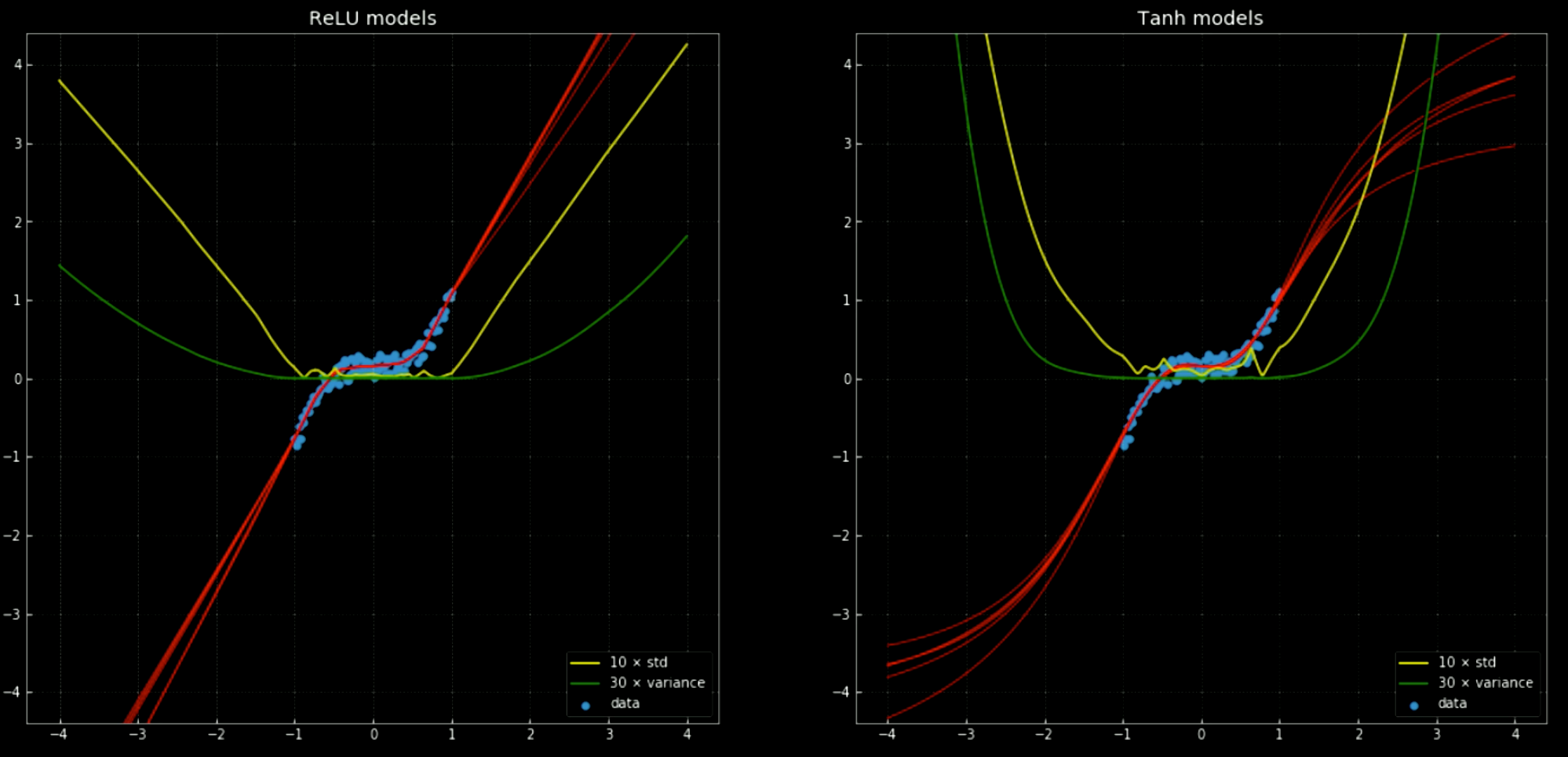
図12 ニューラルネットとその分散と標準偏差。訓練区間の外。
左: 5つの ReLU ネットワーク 右: 5つの tanh ネットワーク

PyTorchを使ってニューラルネットワークを学習するには、5つの基本的なステップが必要です。

1. output = model(input) はモデルの順伝播で、入力を受けて出力を生成します。
2. J = loss(output, target <or> label) はモデルの出力を受け取り、真のターゲットまたはラベルに対する訓練誤差を計算します。
3. model.zero_grad() は勾配計算をクリーンアップし、次のパスに蓄積されないようにします。
4. J.backward() は逆伝播と勾配の蓄積を行います。requires_grad=Trueとなっている各変数$\texttt{x}$について$\nabla_\texttt{x} J$を計算します。これらは各変数の勾配に蓄積されます：$\texttt{x.grad} \gets \texttt{x.grad} + \nabla_\texttt{x} J$。
5. optimiser.step() は、勾配降下法のステップを進め、重みを更新します。

NNを学習する際には、この5つのステップが提示された順に、必要になる可能性が高いです。

---

Shiro Takagi
4 Feb 2020