NNモジュールに対する勾配の計算と、誤差逆伝播法のコツ

誤差逆伝播の具体的な例と基本的なニューラルネットモジュールの導入

例

次に、グラフを用いて誤差逆伝播の具体例を考えます。任意の関数 $G(w)$ をコスト関数 $C$ に入力すると、グラフとして表現できます。ヤコビ行列を乗算する操作によって、このグラフを勾配の逆伝播を計算するグラフに変換することができます(PyTorch と TensorFlow は、ユーザーのために自動的にこれを行うことに注意してください。つまり、順伝播のグラフを自動的に「反転」させて、勾配を逆伝播する微分グラフを作成します)。

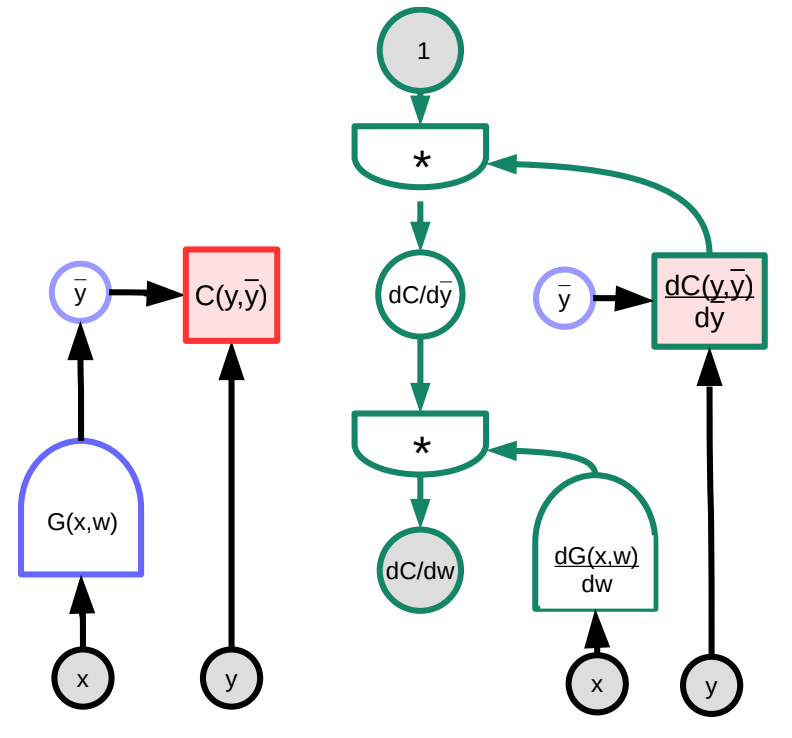
この例では、右の緑のグラフが勾配グラフを表しています。一番上のノードからグラフをたどると、次のようになります。

次元に関していうと、$\frac{\partial C(y,\bar{y})}{\partial w}$ はサイズが $1\times N$ の行ベクトルです。ただし$N$ は $w$の要素の数です。また、$\frac{\partial C(y,\bar{y})}{\partial \bar{y}}$ はサイズが $1\times M$の行ベクトルです。ただし $M$ は出力の次元です。$\frac{\partial \bar{y}}{\partial w}=\frac{\partial G(x,w)}{\partial w}$ はサイズが $M\times N$の行列です。 ただし、$M$ は $G$ の出力の数で、$N$ は$w$の次元です。

グラフのアーキテクチャが固定ではなく、データに依存している場合、複雑な問題が発生する可能性があることに注意してください。例えば、入力ベクトルの長さに応じてニューラルネットモジュールを選択することができます。これは可能ですが、ループの数がそれなりに多くなると、このバリエーションを管理するのが難しくなります。

基本的なニューラルネットのモジュール

おなじみの Linear や ReLU モジュール以外にも、さまざまなタイプの組みこみモジュールが存在します。これらのモジュールは、それぞれの機能を実行するために独自に最適化されているので便利です (他の基本的なモジュールの組み合わせで構築されるのとは対照的です)。

• 線形演算: $Y=W\cdot X$

• ReLU: $y=(x)^+$

  \[\frac{dC}{dX} = \begin{cases} 0 & x<0\\ \frac{dC}{dY} & \text{それ以外} \end{cases}\]

• 複製： $Y_1=X$, $Y_2=X$

  • 両方の出力が入力と等しくなる 「Y - splitter」に似ています。

  • 逆伝播を行うと、勾配の和が得られます。

  • 同様にn本の枝に分けることができます

    \[\frac{dC}{dX}=\frac{dC}{dY_1}+\frac{dC}{dY_2}\]

• 足し算： $y=x_1+x_2$

  • 2つの変数が合計されている状態で、一方が摂動されると、出力は同じ量摂動されます、つまり

    \[\frac{dC}{dX_1}=\frac{dC}{dY}\cdot1 \quad \text{and}\quad \frac{dC}{dX_2}=\frac{dC}{dY}\cdot1\]

• 最大: $Y=\max(X_1,X_2)$

  • この関数は、次のように表すこともできます

    \[Y=\max(X_1,X_2)=\begin{cases} X_1 & X_1 > X_2 \\ X_2 & \text{それ以外} \end{cases} \Rightarrow \frac{dY}{dX_1}=\begin{cases} 1 & X_1 > X_2 \\ 0 & \text{それ以外} \end{cases}\]
  • したがって、連鎖律から、

LogSoftMax vs SoftMax

SoftMaxはPyTorchのモジュールでもあり、数値のグループを0から1の間の正の数値のグループに変換する便利な方法です。これらの数値は確率分布として解釈することができます。その結果、分類問題でよく使われます。下の式の $y_i$ は、すべてのカテゴリの確率のベクトルです。

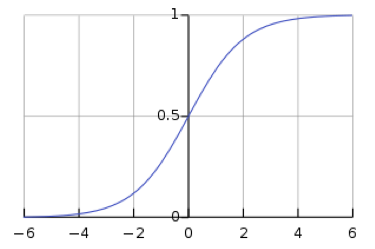
しかし、softmaxを使用すると、ネットワークは勾配消失の影響を受けやすくなります。勾配消失は、下流の重みがニューラルネットワークによって変更されるのを防ぎ、ニューラルネットワークがそれ以上の訓練を完全に止めてしまう可能性があるため、問題となります。1つの値に対するソフトマックス関数であるロジスティックシグモイド関数は、sが大きいときは$h(s)$が1、小さいときは$h(s)$が0であることを示しています。 シグモイド関数は$h(s)=0$と$h(s)=1$では平坦なので、勾配は0となり、勾配消失が発生します。

数学者は、softmaxで作られた勾配が消える問題を解決するために、logsoftmaxのアイデアを思いつきました。LogSoftMaxはPyTorchのもう一つの基本モジュールです。下の式でわかるように、LogSoftMaxはsoftmaxとlogを組み合わせたものです。

下の式は、同じ式を見る別の方法を示しています。下の図は、この関数の「$\log(1 + \exp(s))$」の部分です。sが小さいときは0、大きいときはsになります。結果として出力が飽和せず、勾配消失問題が回避されます。

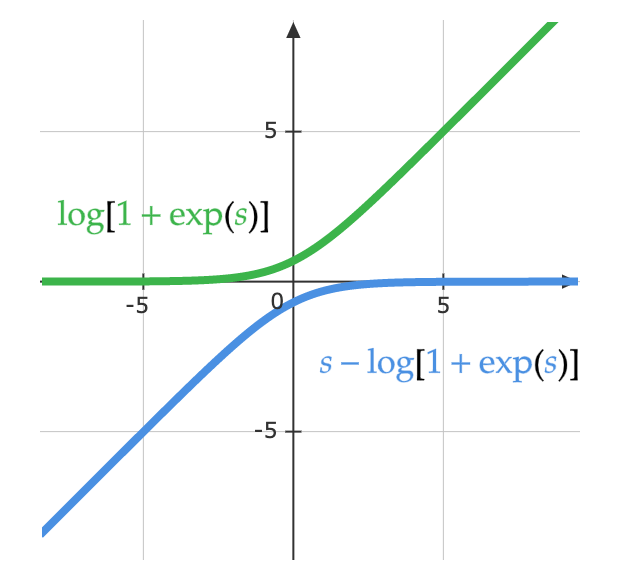
誤差逆伝播法の実応用上のコツ

非線形活性化関数としてReLUを使用

ReLUは層数の多いネットワークに最適で、 シグモイド関数や$\tanh(\cdot)$関数のような代替案が人気を失っています。ReLUが最もよく機能する理由は、その単一のキンクがスケールに関して同変だからでしょう。

分類問題の目的関数としてクロスエントロピー損失を使用

先ほどの講義で説明した Log softmax は、クロスエントロピー損失の特殊なケースです。PyTorchでは、必ずクロスエントロピー損失関数を入力としてlog softmaxを指定してください（通常のsoftmaxではなく）。

学習中のミニバッチで確率的勾配降下法を使用

前述したように、ミニバッチを使うと、データに冗長性があるので、より効率的な学習が可能になります。全ての観測一つ一つについて1ステップで勾配を推定するために予測をしたり誤差を計算したりする必要はありません。

確率的勾配降下法を使う場合、学習例の順序をシャッフル

順番は重要です。もしモデルが各学習ステップで単一のクラスのデータしか見ていない場合、なぜそのクラスを予測すべきなのかを学習せずに、そのクラスを予測するように学習してしまいます。例えば、MNISTのデータセットから数字を分類しようとしていて、データがシャッフルされていない場合、最後の層のバイアス・パラメータは、単純に常に0を予測し、その後、常に1を予測するように適応し、次に2を予測するように適応します。理想的には、すべてのミニバッチにすべてのクラスのサンプルがあるべきです。

しかし、パス（エポック）ごとにサンプルの順番を変える必要があるかどうかについては、現在も議論が続いています。

平均値がゼロで分散が１になるように入力を正規化

学習の前に、各入力特徴量の平均値が0、標準偏差が1になるように正規化しておくと便利です。RGB画像データを使用する場合、各チャンネルの平均と標準偏差を個別に取り、チャンネルごとに正規化するのが一般的です。例えば、データセットに含まれる全ての青の値の平均 $m_b$ と標準偏差 $\sigma_b$ を取り、個々の画像の青の値を次のように正規化します。

ここで $\epsilon$ は、ゼロによる除算を避けるために使う任意の小さな数です。緑と赤のチャンネルについても同じことを繰り返します。これは、異なる照明で撮影した画像から意味のある信号を得るために必要なことです。

学習率を下げるためにスケジュールを使用

学習率は、訓練が進むにつれて低下させるべきです。実際には、ほとんどの高度なモデルは、学習率が一定の単純な SGD の代わりに、学習率を適応させる Adam のようなアルゴリズムを使用して学習します。

重みの減衰には、L1 および/または L2 正則化を使用

重みが大きい場合のペナルティをコスト関数に追加することができます。例えば、L2正則化を使って、損失$L$を定義し、重み$w$を以下のように更新します。

なぜこれを重み減衰と呼ぶのかを理解するために、上の式を書き換えます。すると、更新中に $w_i$ に 1 よりも小さい定数を乗算することになっていることがわかります。

L1正則化(Lasso)は、$\Vert w \Vert^2$の代わりに、$\sum_i \vert w_i\vert$を使用することを除いて、似ています。

本質的に、正則化は、システムに、可能な限り最短の重みベクトルで コスト関数を最小化するように伝えようとします。L1正則化では、役に立たない重みは0に縮小されます。 <!–

Weight initialisation

The weights need to be initialised at random, however, they shouldn’t be too large or too small such that output is roughly of the same variance as that of input. There are various weight initialisation tricks built into PyTorch. One of the tricks that works well for deep models is Kaiming initialisation where the variance of the weights is inversely proportional to square root of number of inputs. –>

重みの初期化

重みはランダムに初期化する必要がありますが、出力が入力とほぼ同じ分散になるように、大きすぎても小さすぎてもいけません。PyTorchには、さまざまな重みの初期化方法が組み込まれています。深層モデルでうまく機能する方法の1つは、重みの分散が入力数の平方根に反比例するKaimingの初期化です。

ドロップアウトを使う

ドロップアウトは正則化の別の形式です。これはニューラルネットのもう一つの層と考えることができます。すなわち、入力を取り、入力のうち $n/2$ をランダムにゼロに設定し、その結果を出力として返すような層です。これにより、システムは少数の入力ユニットに過度に依存するのではなく、すべての入力ユニットから情報を取得することを強制され、その結果、層内のすべてのユニットに情報を分散させることができます。この方法は、Hinton et al (2012)によって最初に提案されました。

より多くのトリックについては、LeCun et al 1998を参照してください。

最後に、誤差逆伝播法はスタックモデルだけでなく、モジュールに部分的な順序がある限り、有向非巡回グラフ（DAG）でも動作することに注意してください。