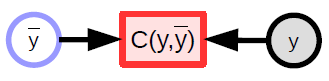勾配法と誤差逆伝播アルゴリズムの紹介

勾配法

パラメトリックモデル

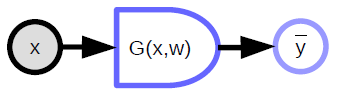
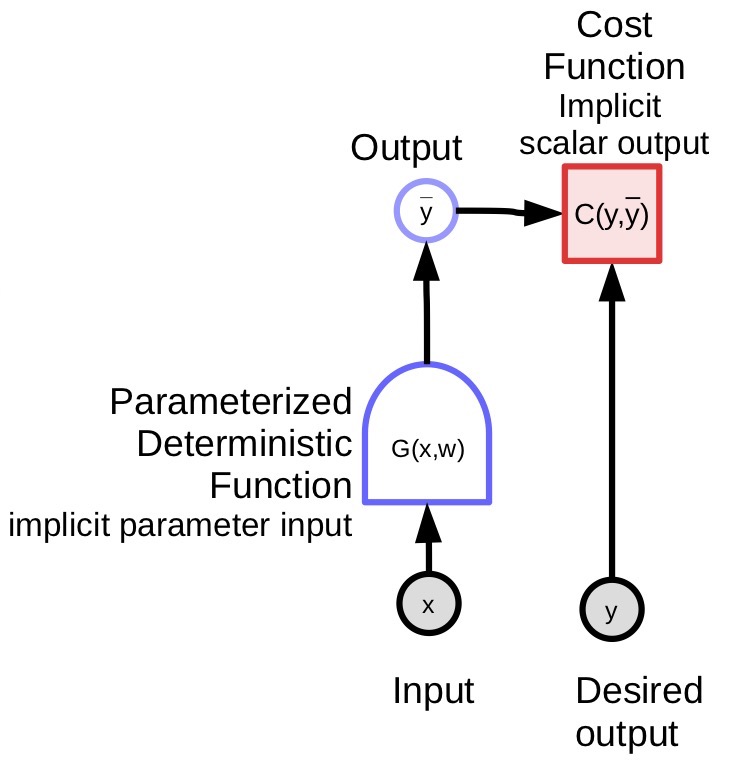
パラメトリックモデルは、単に入力と訓練可能なパラメータに依存する関数です。この2つの間には基本的な違いはありませんが、入力がサンプルごとに異なるのに対し、訓練可能なパラメータは訓練サンプル間で共有されます。ほとんどの深層学習フレームワークでは、パラメータは暗黙的なものであり、関数が呼び出されたときには渡されません。少なくともオブジェクト指向モデルでは、パラメータはいわば「関数の中に保存されている」のです。

パラメトリックモデル（関数）は、入力を受け取り、パラメータベクトルを持ち、出力を生成します。教師あり学習では、この出力はコスト関数($C(y,\bar{y}$))に入り、真の出力(${y}$)とモデルの出力($\bar{y}$)を比較します。このモデルの計算グラフを図1に示します。

| |

パラメータ付けられた関数の例

• 線形モデル - 入力ベクトルの成分の加重和

  \[\bar{y} = \sum_i w_i x_i, C(y,\bar{y}) = \Vert y - \bar{y}\Vert^2\]

• 最近傍 - 入力 $\vect{x}$ と重み行列 $\matr{W}$ があります。出力は、$\vect{x}$に最も近い$\matr{W}$の行に対応する$k$の値です。

  \[\bar{y} = \underset{k}{\arg\min} \Vert x - w_{k,.} \Vert^2\]

  パラメトリックモデルにはより複雑な関数も含まれます。

計算グラフのブロック図による表記

• 変数 (テンソル、スカラー、 連続、 離散)
  • は、観測された、システムへの入力です。
  • は、決定論的な関数によって計算された変数です。

• 決定論的な関数

  

  • 複数の入力を受けて、複数の出力を返すことができます。
  • 暗黙的なパラメータ変数 (${w}$)を持っています。
  • 丸みを帯びた部分は計算しやすい方向を示しています。上の図では、${x}$から${\bar{y}}$を計算する方が、逆よりも計算しやすいことがわかります。

<!–

- Used to represent cost functions
- Has an implicit scalar output
- Takes multiple inputs and outputs a single value (usually the distance between the inputs) -->

• スカラー値関数

  

  • コスト関数を表現するために使われます。
  • 暗黙的なスカラーの出力を持っています。
  • 複数の入力を受けて、単一の出力を返します (通常は入力の間の距離)。

損失関数

損失関数は学習中に最小化される関数です。二つのタイプの損失があります。

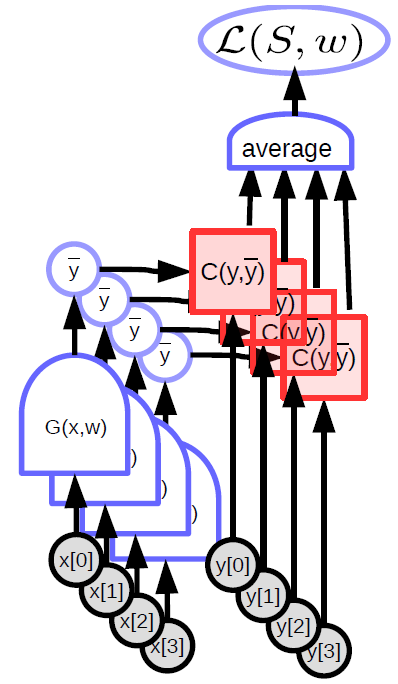
1) サンプルごとの損失 -

2) 平均損失 -

​ 任意のサンプルの集合 \(S = \{(x[p],y[p]) \mid p=0,1...P-1 \}\)　に対して

集合 $S$ の平均損失は次のようになります \(L(S,w) = \frac{1}{P} \sum_{(x,y)} L(x,y,w)\)

図2: 平均損失をもつモデルの計算グラフ

標準的な教師あり学習のパラダイムでは、損失（サンプルあたり）は単にコスト関数の出力です。機械学習は、主に関数の最適化（通常は最小化）に関するものです。また、GANのように2つの関数間のナッシュ均衡を見つけることも含まれます。これは必ずしも勾配降下法とは限りませんが、勾配ベースの手法を用いて行われます。

勾配降下法

勾配に基づく方法は、関数の勾配を簡単に計算できると仮定して、関数の最小値を求める方法/アルゴリズムです。これは、関数が連続的で、ほぼすべての場所で微分可能であることを前提としています（すべての場所で微分可能である必要はありません）。

勾配降下法の直感 - 霧が立ち込める山の中にいることを想像してみてください。あなたは村に下りたいと思っています。視界が限られているので、あなたは自分のすぐ近くを見回して、最も急な下り坂の方向を見つけ、その方向に一歩を踏み出します。

勾配降下法の様々な方法

• 完全な (バッチ) 勾配降下法の更新則

  \[w \leftarrow w - \eta \frac{\partial L(S,w)}{\partial w}\]

• SGD (確率的勾配降下法)については、更新則は次のようになります。

  • $\text{0…P-1}$から$p$を選び、次のように更新します

    \[w \leftarrow w - \eta \frac{\partial L(x[p], y[p],w)}{\partial w}\]

ここで\({w}\)は最適化するパラメータを表しています。

$\eta$はここでは定数ですが、もっと洗練されたアルゴリズムでは、行列などになることもあります。

これが半正定値行列であれば、まだ下山はできますが、必ずしも急な下り坂の方向に移動するとは限りません。実際には、最も急な下り坂の方向は、必ずしも我々が移動したい方向とは限りません。

関数が微分できない、つまり穴があったり階段のようだったり平坦だったりするような場合、勾配は何の情報も与えてくれません。この場合、0次法や勾配なし法と呼ばれる他の方法に頼らなければなりません。ディープラーニングでは、勾配に基づいた方法がすべてです。

しかし、RL(強化学習)では、勾配の明示的な形式を使わずに、勾配の推定を行います。例えば、ロボットが自転車に乗ることを学習することを考えます。この時、ロボットはたまに転んでしまうことがあります。目的関数は、自転車から落ちずにどれくらいの時間留まるかを測定します。残念ながら、目的関数には勾配がありません。ロボットはいろいろなことを試す必要があります。

RLのコスト関数はほとんどの場合微分できませんが、出力を計算するネットワークは勾配ベースです。これが教師あり学習と強化学習の大きな違いです。後者では、コスト関数Cは微分できません。実際、それは完全に未知です。ブラックボックスのように、入力が与えられると出力を返すだけです。これは非常に非効率的であり、RLの主な欠点の1つです。特に、パラメータベクトルが高次元である場合に問題になります（これは、探索するための巨大な解空間を意味し、どこに移動すべきかを見つけるのが困難になります）。

RLで非常に人気のある手法は、actor-critic法です。Critic法は基本的に、既知の訓練可能な第2のモジュールで構成されています。微分可能なCモジュールを訓練して、コスト関数/報酬関数を近似することができます。報酬は負のコストであり、罰のようなものです。これは、コスト関数を微分可能にしたり、少なくとも微分可能な関数で近似したりして、誤差逆伝播法を用いることができるようにする方法です。

従来のニューラルネットにおけるSGDと誤差逆伝播の利点

確率的勾配降下法 (SGD)の利点

実際には、パラメータについての目的関数の勾配を計算するために、確率的な勾配を使用します。確率的な勾配は、すべてのサンプルの平均である完全な勾配を計算する代わりに、1つのサンプルを取り、損失$L$およびその損失のパラメータに関する勾配を計算します。そして、負の勾配の方向に1ステップ更新するだけです。

式の中では、与えられたサンプル($x[p]$,$y[p]$)毎の損失関数のパラメータに関する勾配にステップサイズをかけたものを、$w$から引くことで、$w$に近づけています。

これを1つのサンプルで行うと、図3に示すような非常にノイズの多い軌跡が得られます。損失が直接下降していくのではなく、確率的に降下しています。すべてのサンプルが損失を異なる方向に引き寄せます。それは、平均値の最小値に引っ張られているだけです。効率が悪いように見えますが、少なくとも機械学習の文脈では、サンプルに冗長性がある場合には、バッチ勾配降下法よりもはるかに高速です。

| |

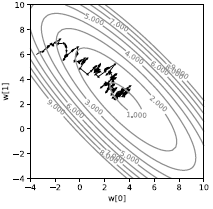
実際には、単一のサンプルで確率的勾配降下法を行う代わりにバッチを使用します。私たちは、単一のサンプルではなく、サンプルのバッチにわたって勾配の平均を計算し、その後、1ステップ更新します。これを行う理由は、単に、バッチを使用した方が並列化が容易なので、既存のハードウェア（GPUやマルチコアCPUなど）をより効率的に利用できるからです。並列化するにはバッチが一番簡単です。

従来のニューラルネットワーク

従来のニューラルネットでは、基本的に線形演算と要素ごとの非線形演算の層が散在しています。線形演算については、概念的には行列-ベクトルの乗算にすぎません。（入力）ベクトルに重みで形成された行列を乗算したものを取ります。第二のタイプの演算は、加重和ベクトルの全成分を取り、単純な非線形関数(例えば、$\texttt{ReLU}(\cdot)$, $\tanh(\cdot)$, ….)を通過させるものです。

|

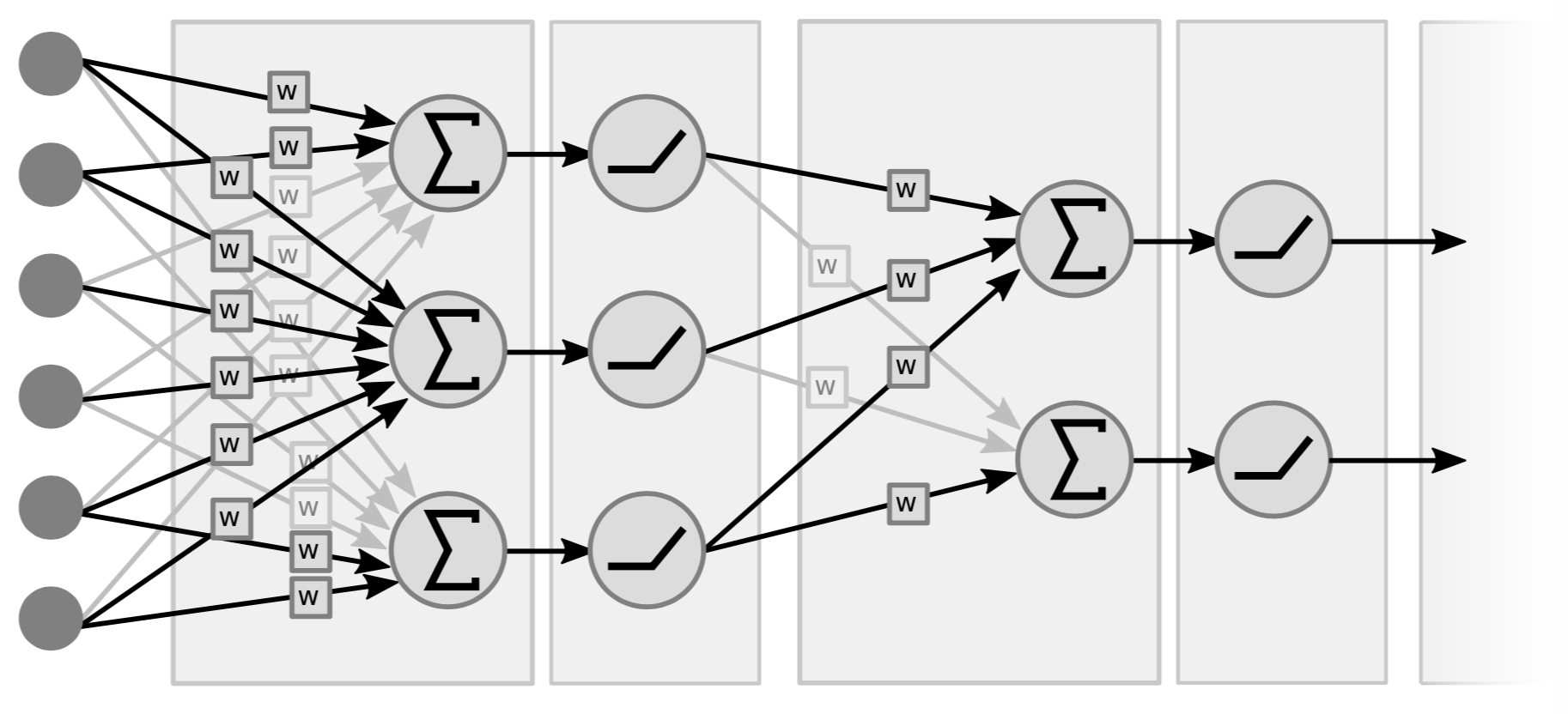
図4は2層ネットワークの例ですが、重要なのはペア（つまり線形+非線形）です。変数を数えるので3層ネットワークと呼ぶ人もいます。もし中間層に非線形性がなければ、2つの線形関数の積が線形関数になるので、1層にしてもよいことに注意してください。

図5は、ネットワークの線形関数ブロックと非線形関数ブロックがどのように積み重なっているかを示しています。

|

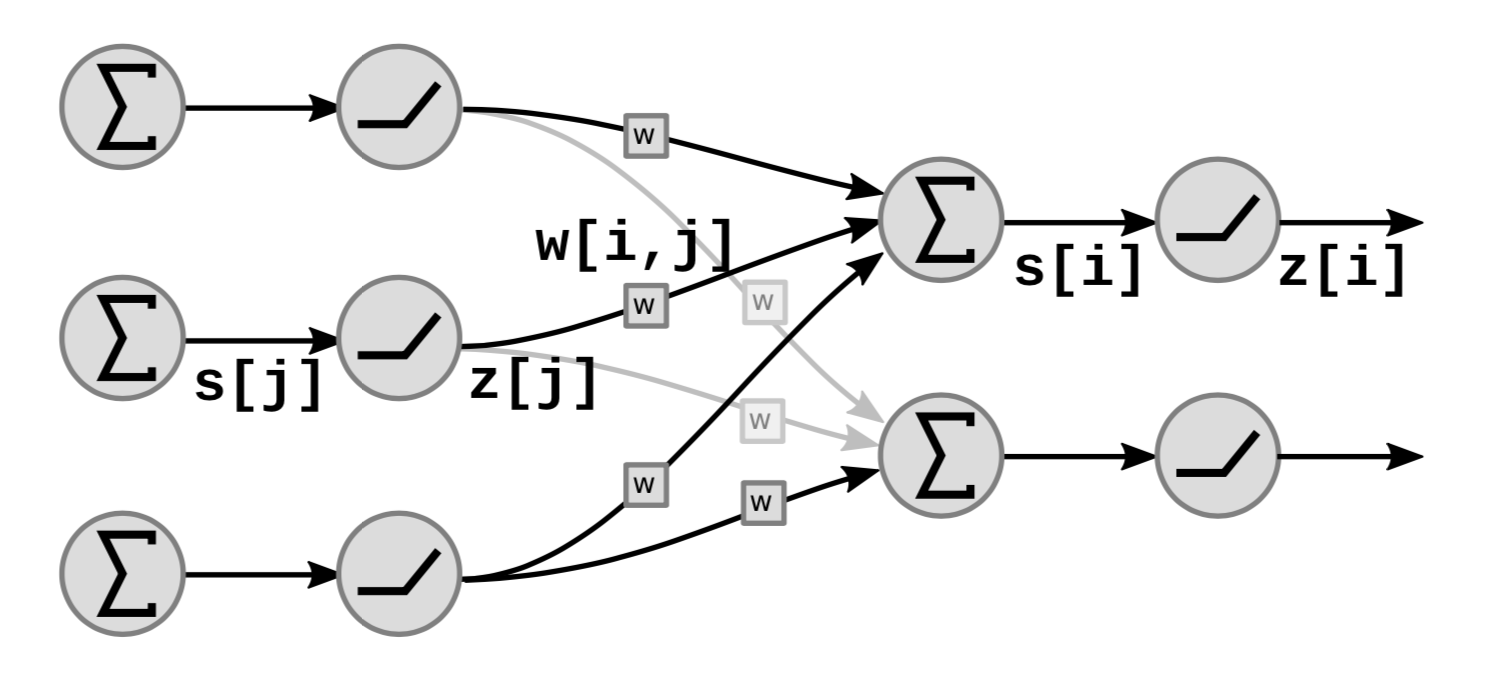
このグラフでは、$s[i]$はユニット${i}$の重み付き和で、次のように計算されます

ここで、$UP(i)$は$i$に入ってくるものを表し、$z[j]$は前のレイヤーからの$j$番目の出力です。

出力 $z[i]$ は次のように計算されます。

ここで$f$は非線形関数です。

非線形関数を通した誤差逆伝播法

誤差逆伝播を行う最初の方法は、非線形関数を通して誤差逆伝播を行うことです。ネットワークから特定の非線形関数 $h$ を取り出し、他のすべてをブラックボックスに入れておきます。

|

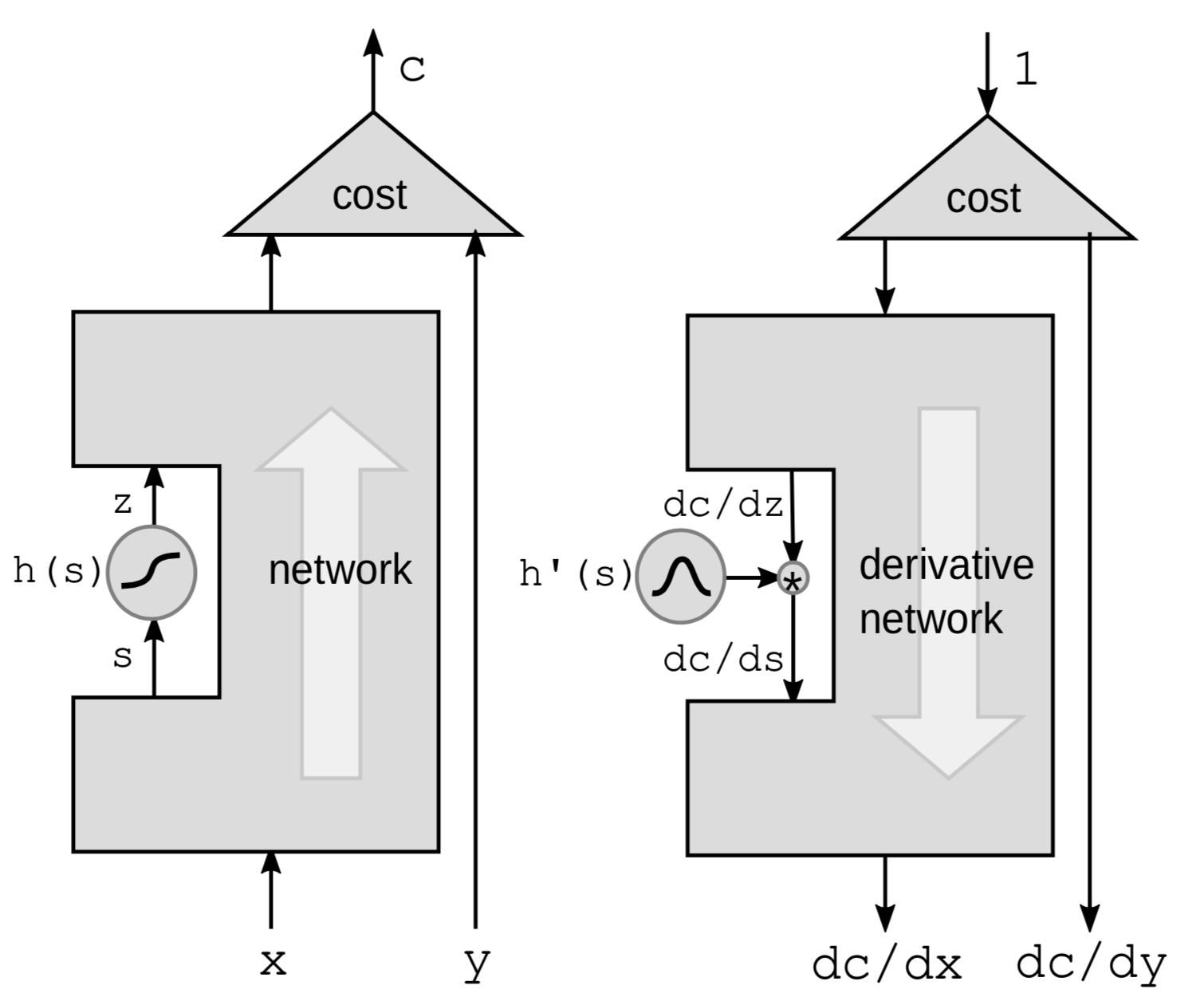
勾配を計算するために連鎖律を用います

ここで、$h’(s)$は、$s$についての$z$の微分で、$\frac{\mathrm{d}z}{\mathrm{d}s}$で表されます。 微分同士の関係を明確にするために、上の式を次のように書き換えます

したがって、もしネットワーク内にこれらの関数の連鎖があるならば、すべての${h}$ 関数の微分を乗算して誤差逆伝播し、入力層に戻ることができます。

摂動を加えるという観点から考えると、より直感的です。sを$\mathrm{d}s$で摂動すると、次のように$z$を摂動することになります

そしてこれは下のようにCを摂動することになります

もう一度、上に示したのと同じような式を得ることができました。

重み付き和を通した誤差逆伝播

線形モジュールに対しては、重み付き和を用いて誤差逆伝播を行います。ここでは、${z}$変数から$s$変数たちに向かう3つの接続を除いて、ネットワーク全体をブラックボックスとみなしています。

| |

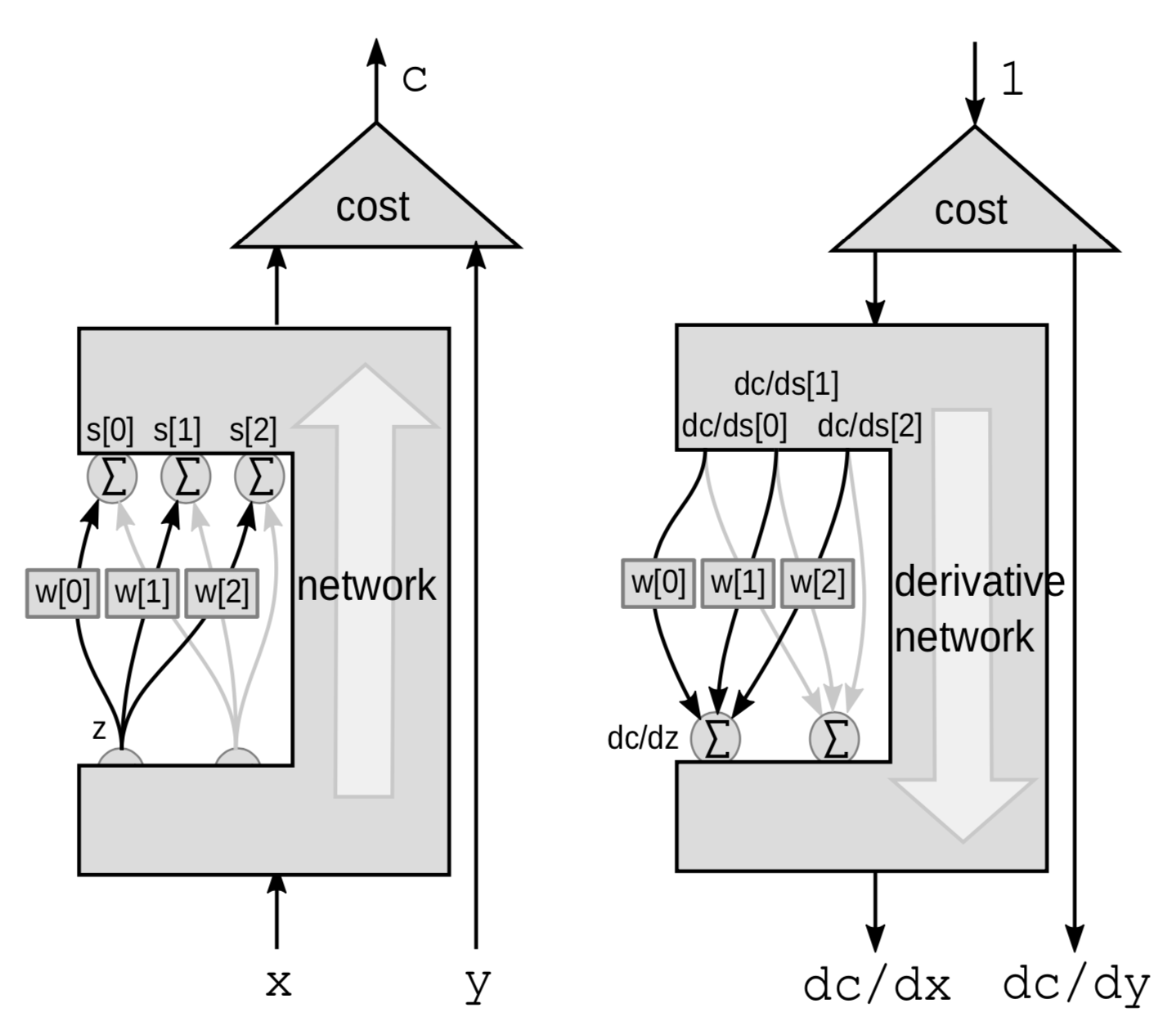
今回は摂動は重み付き和です。Zは様々な変数に影響します。$z$を$\mathrm{d}z$で摂動すると、$s[0]$, $s[1]$ そして $s[2]$を次のように摂動します

これはCを次のように摂動します

したがって、Cは3つの変化の合計によって変化することになります

ニューラルネットワークと一般化された誤差逆伝播のPyTorch実装

従来のニューラルネットのブロック図による表記

• 線形ブロック $s_{k+1}=w_kz_k$

• 非線形ブロック $z_k=h(s_k)$

  

それぞれ、$w_k$: 行列、 $z_k$: ベクトル、 $h$: スカラー関数${h}$を各成分に適用したもの、です。これは線形関数と非線形関数のペアを持つ3層のニューラルネットです。最近のニューラルネットの多くはこのような明確な線形と非線形の分離がなく、より複雑ですが。

PyTorch実装

import torch
from torch import nn
image = torch.randn(3, 10, 20)
d0 = image.nelement()

class mynet(nn.Module):
    def __init__(self, d0, d1, d2, d3):
        super().__init__()
        self.m0 = nn.Linear(d0, d1)
        self.m1 = nn.Linear(d1, d2)
        self.m2 = nn.Linear(d2, d3)

    def forward(self,x):
        z0 = x.view(-1)  # flatten input tensor
        s1 = self.m0(z0)
        z1 = torch.relu(s1)
        s2 = self.m1(z1)
        z2 = torch.relu(s2)
        s3 = self.m2(z2)
        return s3
model = mynet(d0, 60, 40, 10)
out = model(image)

• PyTorchでは、オブジェクト指向クラスを使ってニューラルネットを実装することができます。まず、ニューラルネットのクラスを定義し、コンストラクタで定義済みの nn.Linear クラスを使って線形層を初期化します。線形層は、それぞれにパラメータベクトルが含まれているので、別々のオブジェクトにする必要があります。nn.Linearクラスはバイアスベクトルも暗黙的に追加します。そして、$\text{torch.relu}$関数を非線形活性化関数として、出力を計算するためのフォワード関数を定義します。relu関数はパラメータを持たないので、個別に初期化する必要はありません。

• PyTorchはフォワード関数に対してどのように勾配を計算して伝播させるのかを知っているので、実装する人が陽に勾配を計算する必要はありません。

関数モジュールを通した誤差逆伝播

より一般化された誤差逆伝播の式を示します。

| |

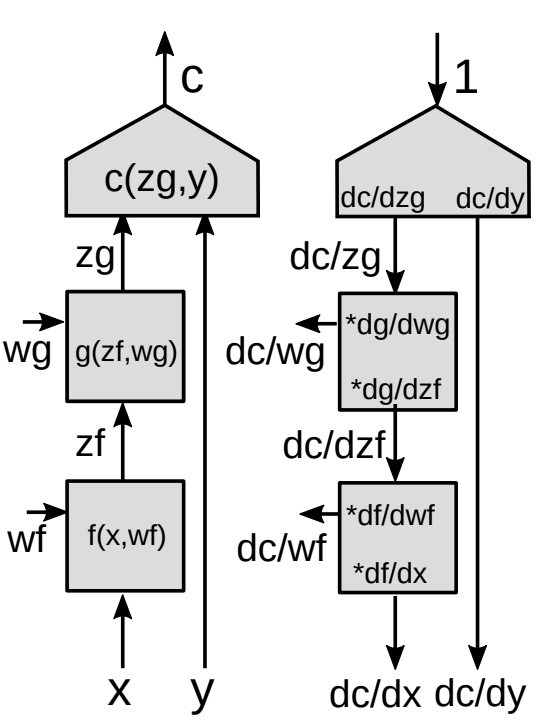
• ベクトル関数に対して連鎖律を適用して、

  \[z_g : [d_g\times 1]\] \[z_f:[d_f\times 1]\] \[\frac{\partial c}{\partial{z_f}}=\frac{\partial c}{\partial{z_g}}\frac{\partial {z_g}}{\partial{z_f}}\] \[[1\times d_f]= [1\times d_g]\times[d_g\times d_f]\]

  これは、連鎖律を使った $\frac{\partial c}{\partial{z_f}}$ の基本式です。スカラー関数のベクトルに対する勾配は、微分するベクトルと同じ大きさのベクトルであることに注意してください。表記に一貫性を持たせるために、列ベクトルではなく行ベクトルとしています。

• ヤコビ行列

  \[\left(\frac{\partial{z_g}}{\partial {z_f}}\right)_{ij}=\frac{(\partial {z_g})_i}{(\partial {z_f})_j}\]

  $z_g$についてのコスト関数の勾配が与えられたもとで、$z_f$に対するコスト関数の勾配を計算するために、 $\frac{\partial {z_g}}{\partial {z_f}}$ (ヤコビ行列の要素)が必要です。各要素 $ij$ は、入力ベクトルの $j$ 番目の成分に対する出力ベクトルの $i$ 番目の成分の偏微分に等しいです。

  モジュールが連なっている場合、すべてのモジュールのヤコビ行列を乗算し続けると、すべての内部変数の勾配が得られます。

マルチステージグラフを通した誤差逆伝播

図9に示すように、ニューラルネットワークの多くのモジュールのスタックを考えてみましょう。

|

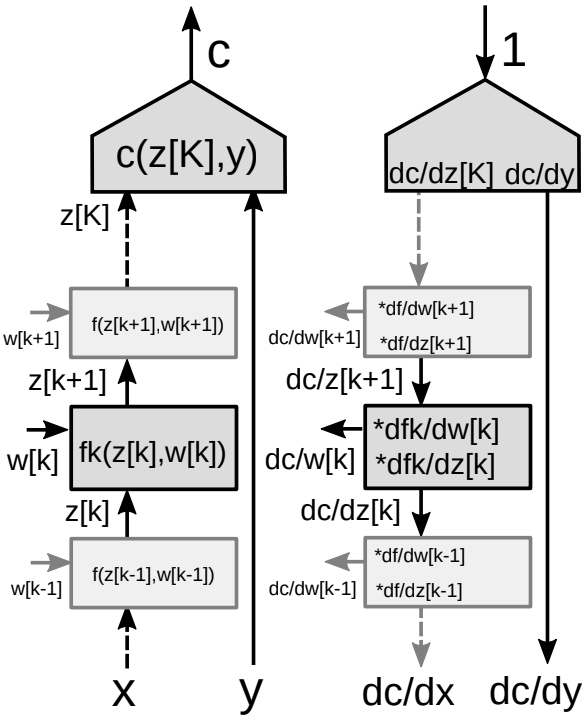
• ベクトル関数に連鎖律を使う

  \[\frac{\partial c}{\partial {z_k}}=\frac{\partial c}{\partial {z_{k+1}}}\frac{\partial {z_{k+1}}}{\partial {z_k}}=\frac{\partial c}{\partial {z_{k+1}}}\frac{\partial f_k(z_k,w_k)}{\partial {z_k}}\] \[\frac{\partial c}{\partial {w_k}}=\frac{\partial c}{\partial {z_{k+1}}}\frac{\partial {z_{k+1}}}{\partial {w_k}}=\frac{\partial c}{\partial {z_{k+1}}}\frac{\partial f_k(z_k,w_k)}{\partial {w_k}}\]

• モジュールに関する二つのヤコビ行列
  • $z[k]$に関するもの
  • $w[k]$に関するもの