問題のモチベーション、線形代数、そして可視化

リソース

Alfredo Canziani Twitter @alfcnzをフォローしてください。線形代数や特異値分解(SVD)に関する詳細なビデオや教科書は、Alfredoのツイッターで検索することができます。例えばlinear algebra (from:alfcnz)と検索してみてください。

変換とモチベーション

動機を与える例として、画像の分類を考えてみましょう。1メガピクセルのカメラで写真を撮ったとします。この画像は、縦に約1,000ピクセル、横に約1,000ピクセルの画素を持ち、各画素は赤、緑、青（RGB）の3つの色の次元を持っています。それぞれの画像は、300万次元空間の1点と考えることができます。このような巨大な次元により、犬と猫のように分類したいと思うような興味深い画像は、本質的に空間の同じ領域に存在することになります。

これらの画像を効果的に分離するために、点を移動させるためのデータの変換方法を考えます。2次元空間では、線形変換は行列積と同じであることを思い出してください。例えば、以下のような線形変換があります。

• 回転（行列が正規直交の場合）
• 拡大縮小（対角行列の場合）
• 鏡映（行列式が負の場合）
• せん断

0 が常に 0 に写像されるとは限らないので、平行移動だけでは線形ではないことに注意してください。画像の例に戻ると、点が0の周りにクラスタリングされるように変換し、その領域に「ズームイン」するように対角行列でスケーリングすることで、データ点を変換することができます。最後に、異なる点をそれぞれのクラスに分ける線を空間全体に見つけることで、分類を行うことができます。言い換えれば、線形変換と非線形変換を使って、点を線形分離可能な空間にマッピングするという考え方です。この考え方は、次の節でより具体的に説明します。

データの可視化 - ネットワークを使って色で点を区切る

この可視化では、5つの枝を持つ螺旋があり、それぞれの枝は異なる色に対応しています。点は２次元平面上にあり、タプルとして表現することができます。色は三次元を表現しており、これは各点ごとに異なるクラスであると考えることができます。そして、ネットワークを使用して、各点を色で区切ります。

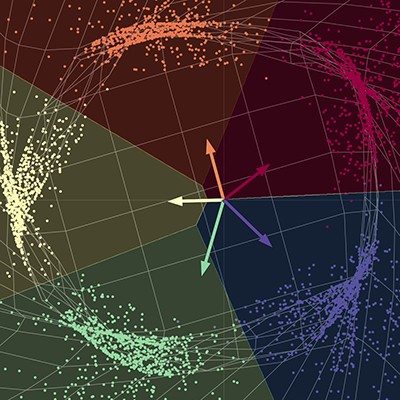(a) 入力点、ネットワークに通す前	(b) 出力点、ネットワークに通した後

ネットワークは、それぞれの点を異なる部分空間に分離するために、空間構造を引き伸ばします。収束すると、ネットワークは、最終的な多様体の異なる部分空間に各色を分離します。言い換えれば、この新しい空間の色のそれぞれは、１対すべての回帰において線形分離可能になります。図中のベクトルは、5×2の行列で表すことができます。この行列は、各点に乗算することで、5つの色のそれぞれのスコアを返すことができます。ここでは、出力次元は5で、色ごとに1つずつ、入力次元は2で、それぞれ点xとyの座標に1つずつです。要約すると、このネットワークは基本的に空間構造を受け取り、いくつかの行列と非線形性によってパラメトライズされた空間の変換を行います。

ネットワークアーキテクチャ

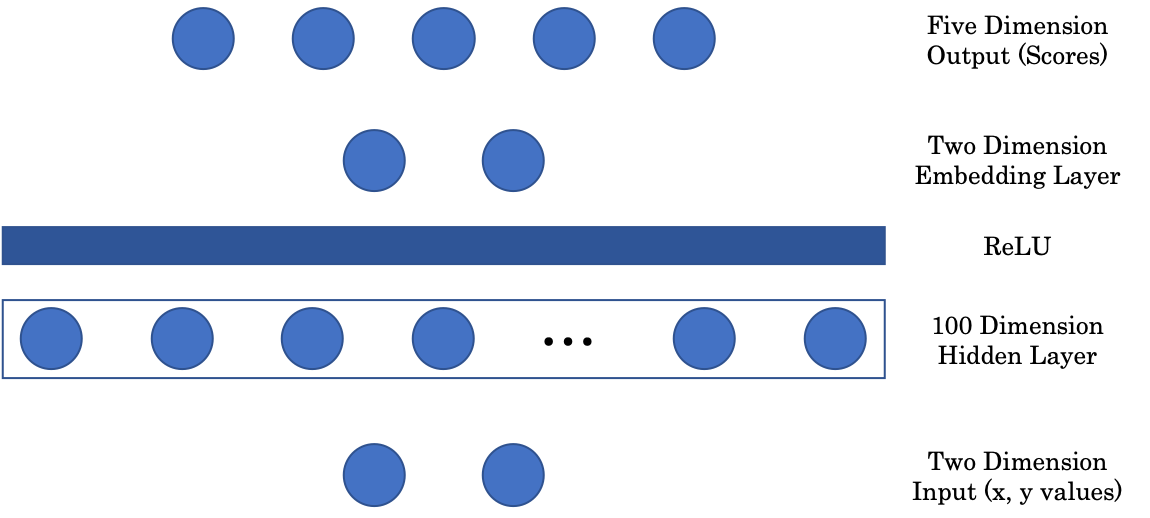
図2: ネットワークアーキテクチャ

最初の行列は、2次元の入力を100次元の隠れ層にマッピングします。次に、非線形層、ReLU（Rectified Linear Unit）ですが、これは単に正の部分 を返す関数$(\cdot)^+$です。そして、画像をグラフィカルに表示するために、100次元の隠れ層の入力を2次元の出力にマッピングする埋め込み層を加えます。最後に、埋め込み層は、各色のスコアを表すネットワークの最終的な5次元の層に射影します。

ランダム射影 - Jupyter Notebook

Jupyter Notebook は ここから見つかります。このノートブックを動かすためには、README.mdで説明されているようなpDL環境をインストールしていなければなりません。

PyTorch device

PyTorch はコンピュータの CPU と GPU の両方で動作します。CPUはシーケンシャルなタスクに、GPUはパラレルなタスクに適しています。目的のデバイスで実行する前に、まず、テンソルとモデルがデバイスのメモリに転送されていることを確認する必要があります。これは以下の2行のコードで行うことができます。

device = torch.device("cuda:0" if torch.cuda.is_available() else "cpu")
X = torch.randn(n_points, 2).to(device)

最初の行では、deviceという変数を作成し、GPUが利用可能であればGPUに代入します。次の行では、.to(device)を呼び出すことでテンソルが作成され、デバイスのメモリに送られます。

Jupyter Notebookのヒント

ノートブックのセル内の関数のドキュメントを見るには、Shift + Tabを押してください。

線形変換の可視化

線形変換は行列として表現できることを思い出してください。特異値分解を用いて、行列を、それぞれ異なる線形変換を表す3つの成分行列に分解することができます。

式(1)において、行列 $U$ と $V^\top$ は互いに直交する行列で、それぞれ回転変換と鏡映変換を表しています。真ん中の行列は対角行列で、スケーリング変換を表しています。

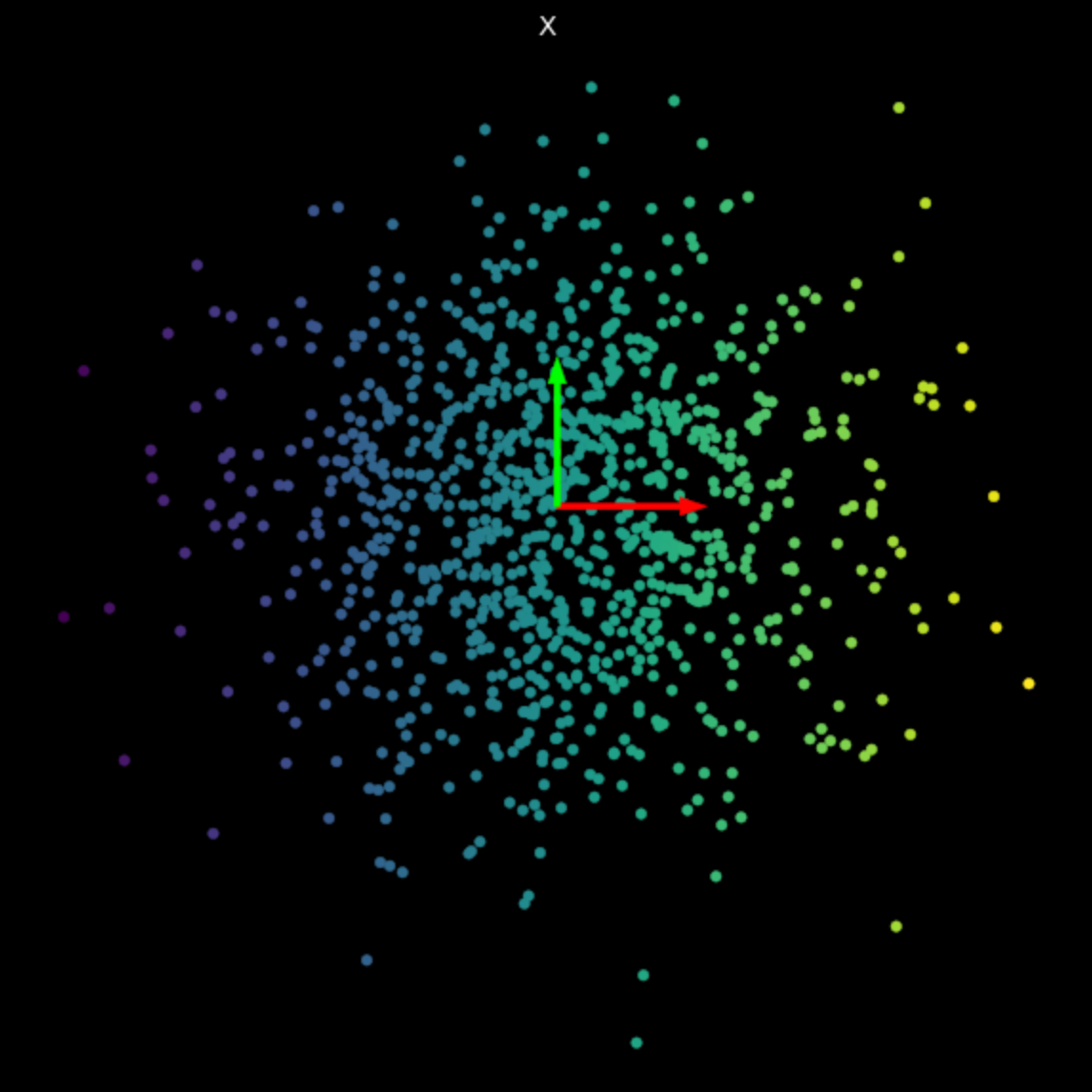
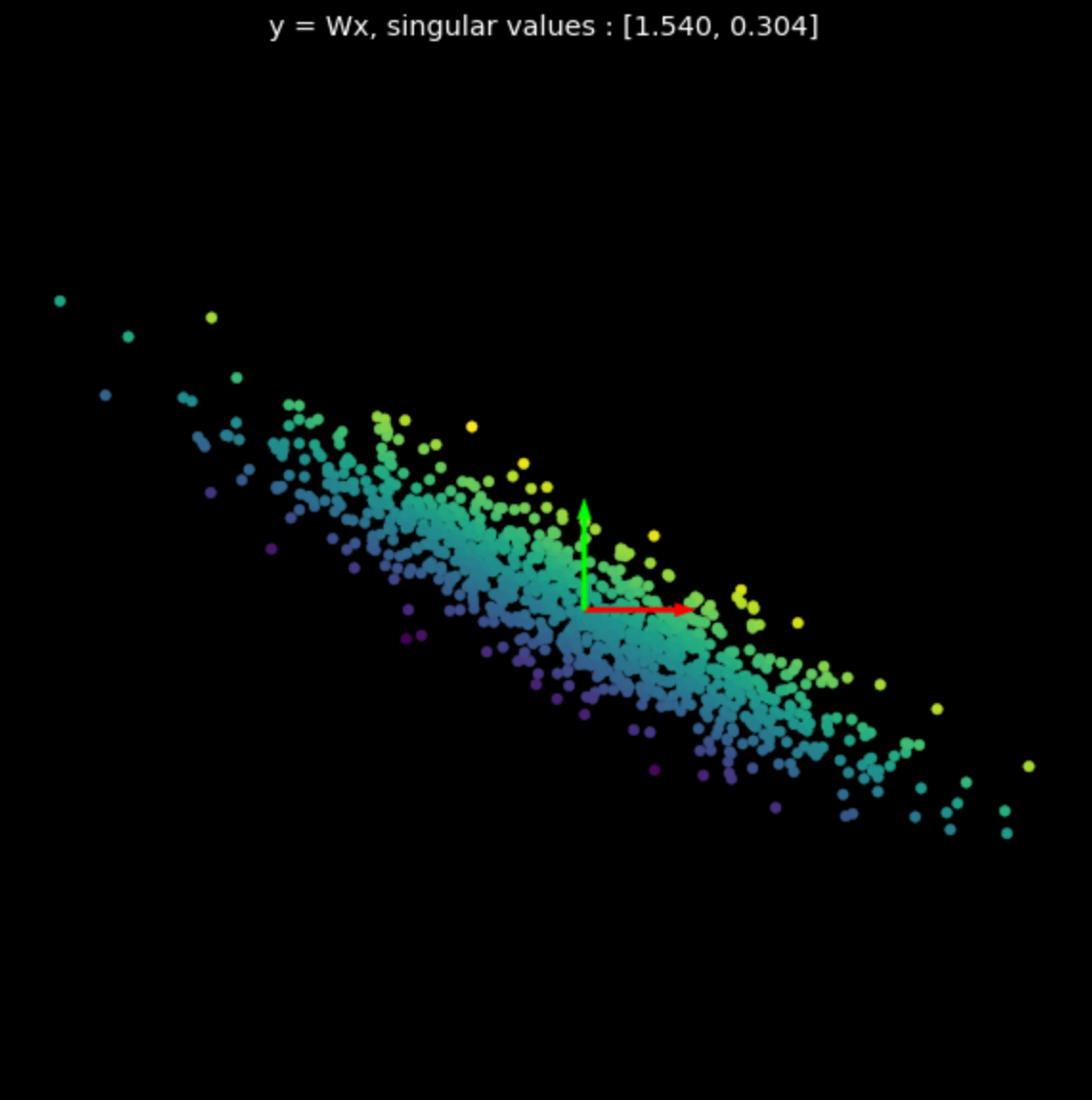
いくつかのランダムな行列の線形変換を図3に示します。特異値が結果の変換に与える影響に注目してください。

使用した行列は Numpy で生成したものですが、PyTorch の nn.Linear クラスで bias = False を指定して線形変換を行うこともできます。

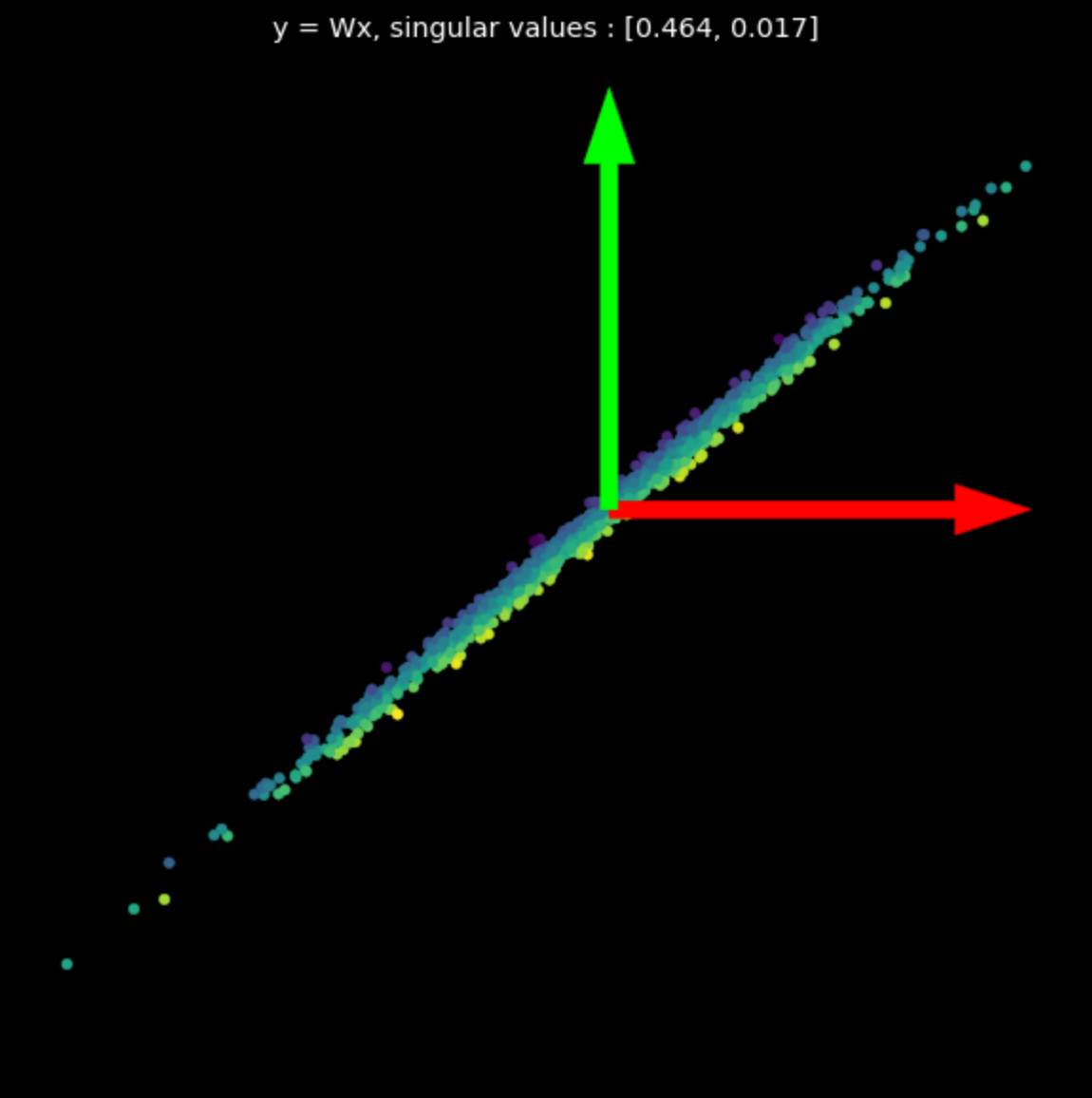(a) Original points	(b) $s_1$ = 1.540, $s_2$ = 0.304	(c) $s_1$ = 0.464, $s_2$ = 0.017

非線形変換

次に、下の変換を可視化します。

図４の$\tanh(\cdot)$の図を思い出してください。

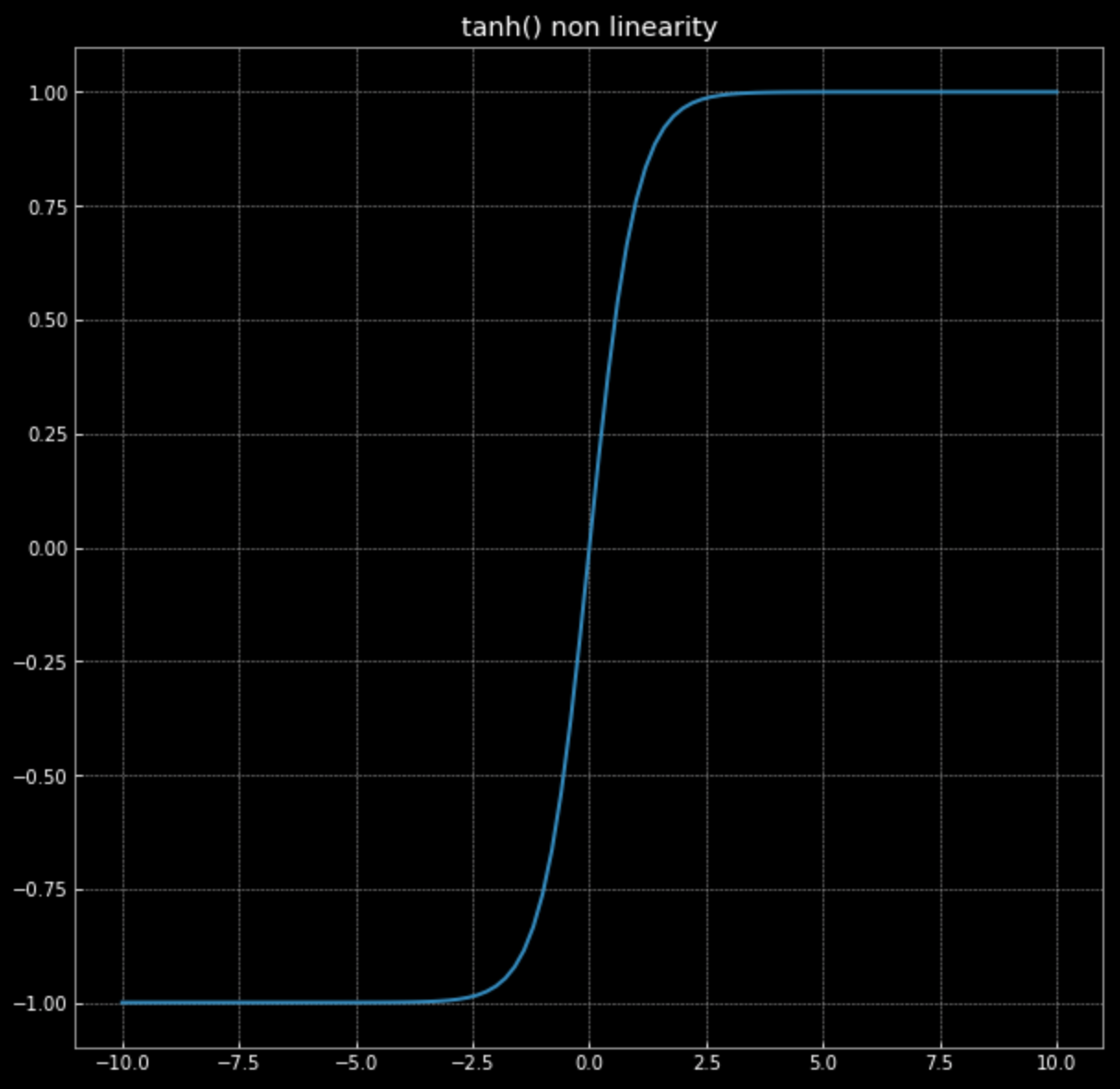
図4: tanh非線形性

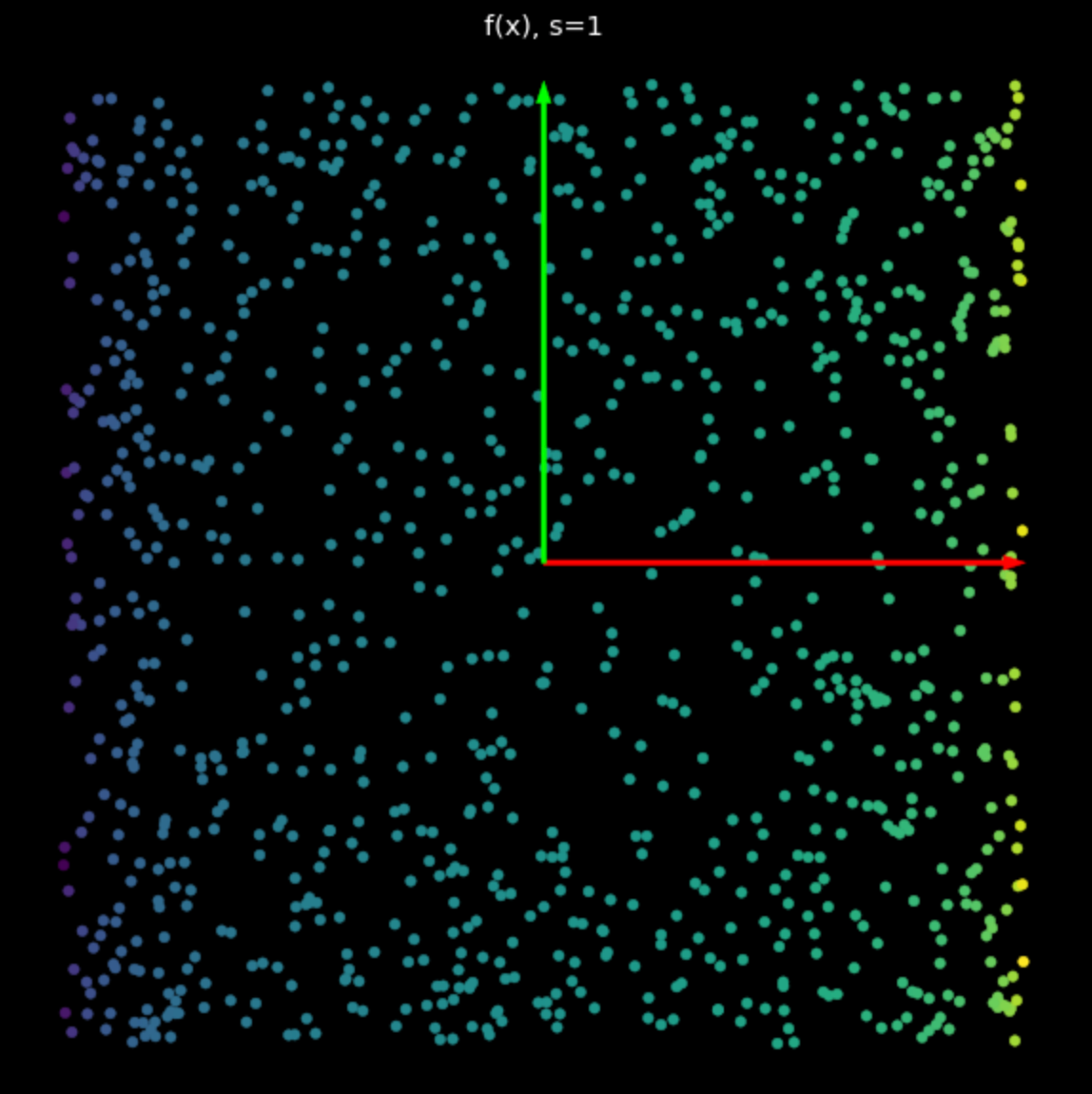
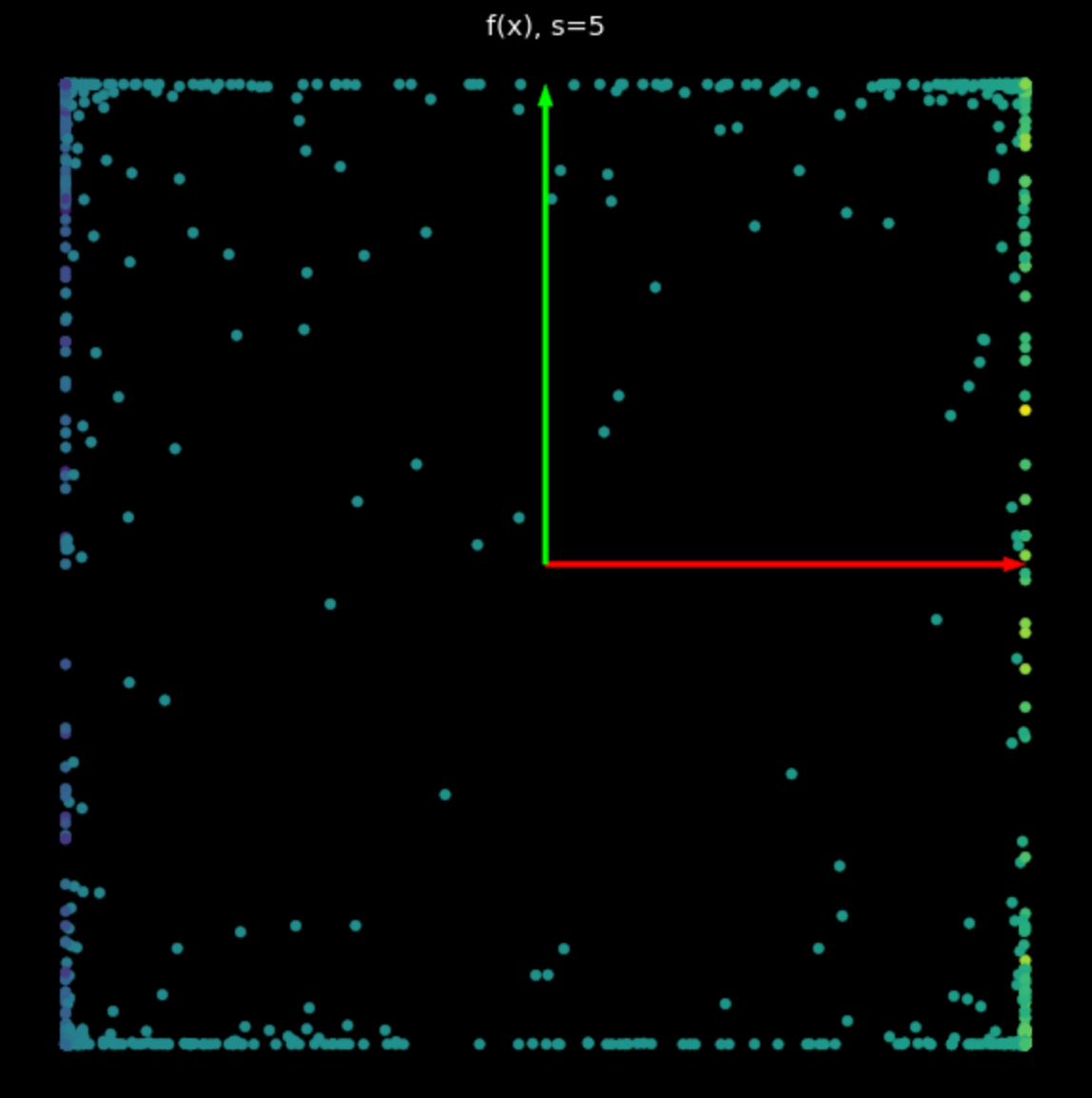
この非線形性は、$-1$ と $+1$ の間の点を束縛し、正方形を作ります。(2)式の $s$ の値が大きくなるにつれて、より多くの点が正方形の端に押し出されます。これを図5に示します。より多くの点を周辺に押し付けることで、点をより大きく広げることができ、これによって分類を試みることができます。 <!– | | | | (a) Non-linearity with $s=1$ | (b) Nonlinearity with $s=5$ |

–>

(a) $s=1$の非線形性	(b) $s=5$の非線形性

ランダムニューラルネット

最後に、単純な、訓練されていないニューラルネットワークによって実行される変換を可視化します。このネットワークは、アフィン変換を行う線形層、tanh非線形、そして最後に別の線形層から構成されています。図6の変換を見てみると、先ほどの線形変換や非線形変換とは異なることがわかります。今後、ニューラルネットワークによるこれらの変換を、最終的な目的である分類に役立てるにはどうすればよいかを見ていきます。

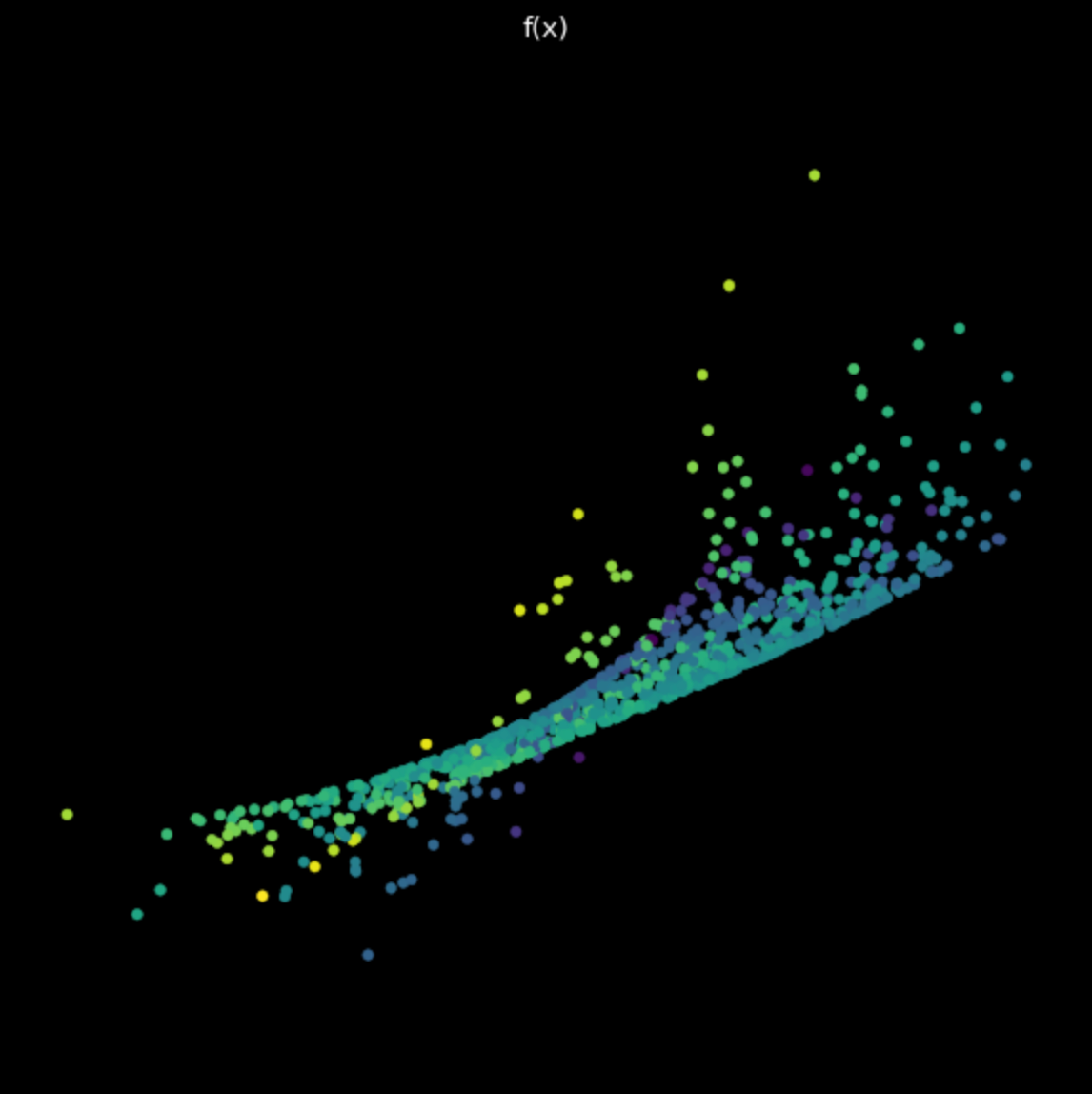
図6: 学習されていないニューラルネットによる変換