Articolo "Prediction and Policy learning Under Uncertainty" (PPUU)

Introduzione e impostazione del problema

Supponiamo di voler imparare a guidare utilizzando l’apprendimento delle politiche (policy/reinforcement learning, RL) senza avere un modello della realtà (model-free). Nel RL, addestriamo i modelli permettendogli di compiere degli errori ed imparare da essi. Questo però non è il metodo migliore (per imparare a guidare) dato che un errore potrebbero portarci in paradiso/all’inferno, e quindi l’apprendimento diventa inutile.

Consideriamo un modo più “umano” di imparare a guidare una macchina. Consideriamo un esempio in cui bisogna cambiare corsia. Presupponiamo che la macchina si muova a 100 km/h, che sono più o meno 30 miglia/s, se guardiamo 30 miglia in avanti, è come guardare nel futuro di 1 secondo.

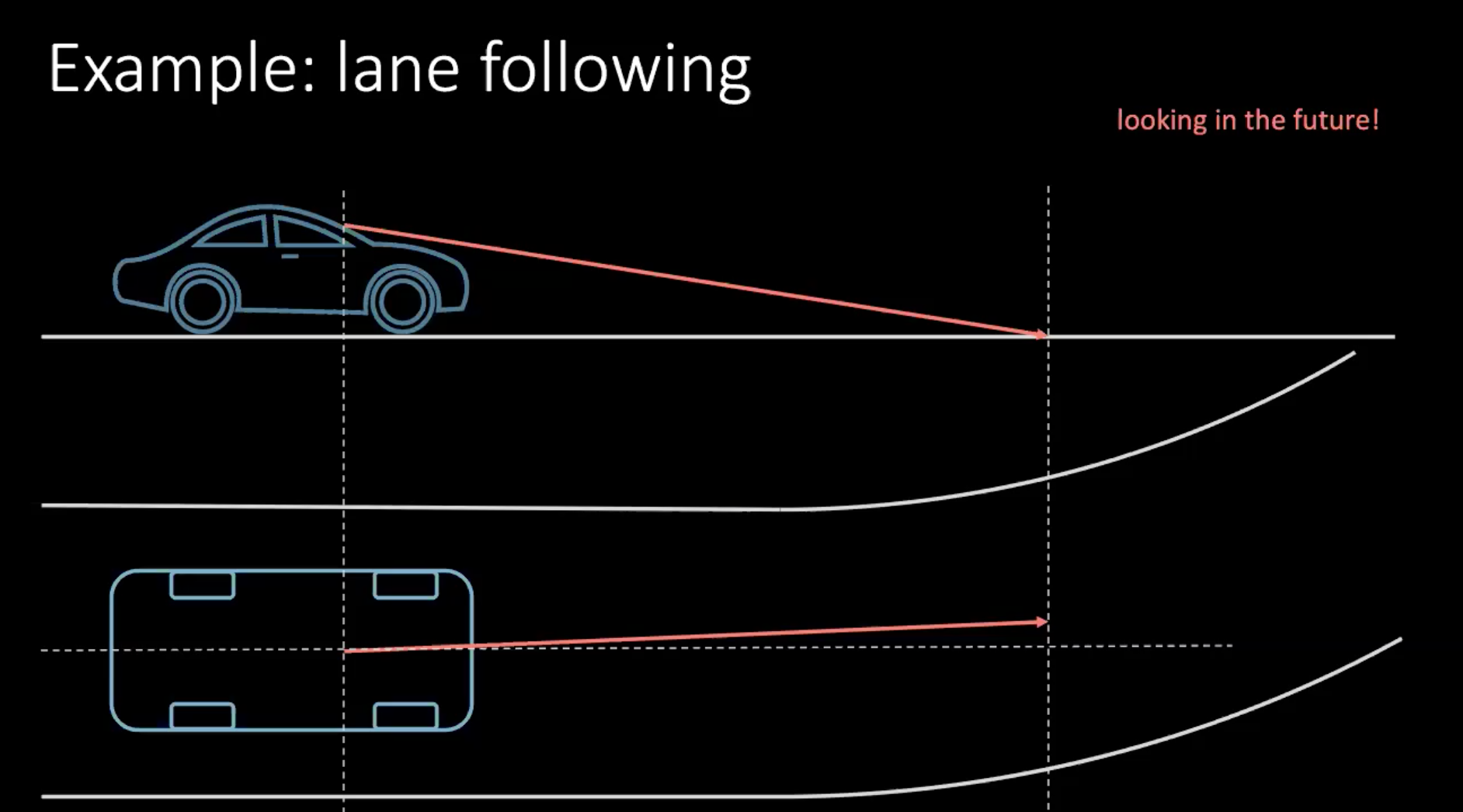
Fig. 1: Guardando il futuro durante la guida

Se dovessimo girare la macchina, dovremmo prendere una decisione basata sul futuro imminente. Per girare fra un paio di metri, compiamo un’azione adesso, che in questo contesto significa girare il volante. Prendere una decisione non dipende solo dall’autista ma anche dagli altri veicoli circondanti la macchina nel traffico. Dato che non sappiamo in maniera deterministica come si muoveranno i veicoli che abbiamo attorno, è molto difficile tenere conto di tutte le possibilità.

Cerchiamo di capire meglio quello che succede in questo scenario. Abbiamo un agente (qui rappresentato da un cervello) che prende l’input $s_t$ (la posizione, velocità e le immagini del contesto) e produce un’azione $a_t$ (il controllo del volante, l’accelerazione, e i freni). Compiendo l’azione sull’ambiente ci troviamo in un nuovo stato, che ha un costo $c_t$.

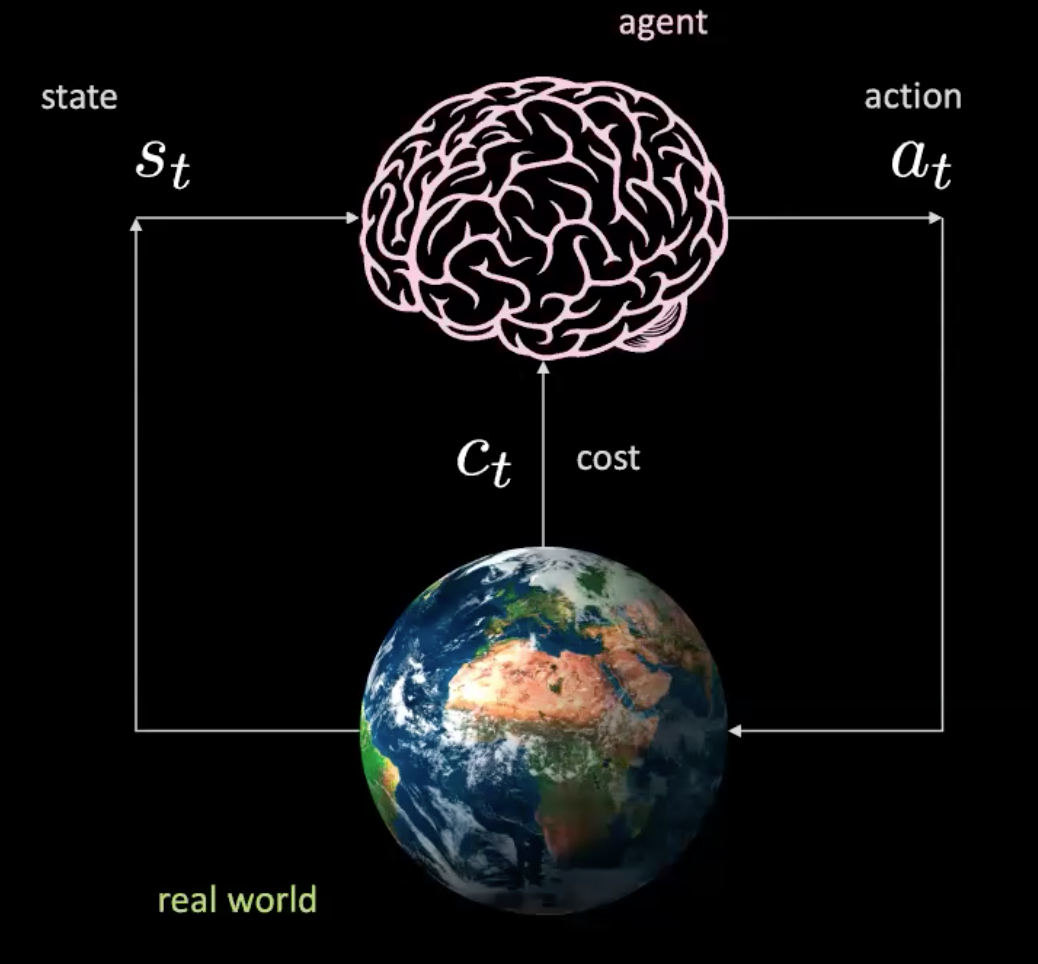
Fig. 2: Illustrazione di un agente nella realtà

Questo è come una rete semplice in cui possiamo prendere azioni secondo lo stato specifico in cui ci troviamo, e poi la realtà ci mostra il prossimo stato e le consequenze delle nostre azioni. Questo è un sistema “privo di modelli” (model-free) perché con ciascun’azione interagiamo con la realtà. Ma possiamo addestrare un agente senza dover interagire con la realtà?

Si, possiamo! Scopriamo come farlo nella sezione “Apprendimento di un modello della realtà”.

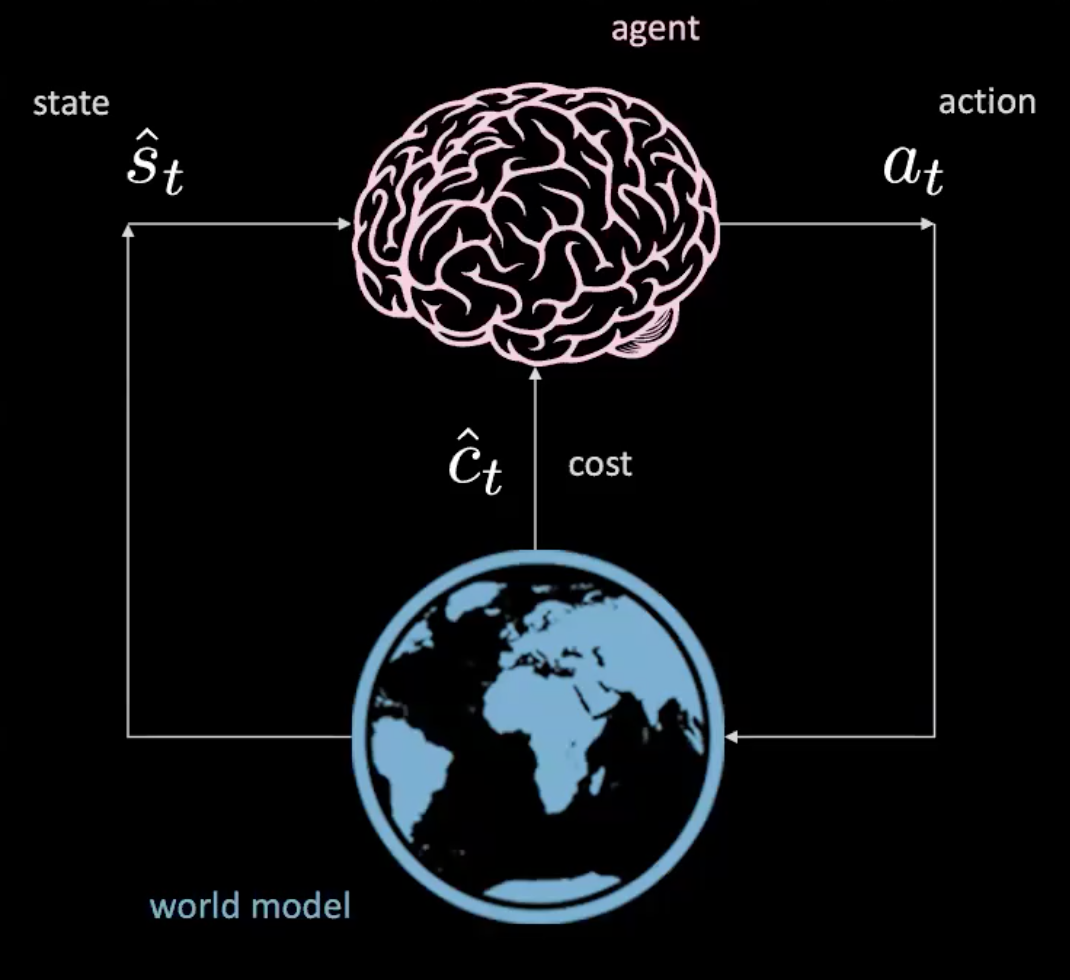
Fig. 3: Illustrazione di un agente nel modello della realtà

Dati

Prima di discutere di come apprendere il modello della realtà, esploriamo i dati che abbiamo. Abbiamo 7 telecamere montate sopra ad un palazzo di 30 piani che si affaccia sull’autostrada interstatale. Aggiustiamo le telecamere per ottenere una visuale dall’alto verso il basso top-down e poi estraiamo le “scatole” che definiscono il confine (bounding box) di ciascun veicolo. Nel periodo $t$, possiamo determinare $p_t$ che rappresenta la posizione della macchina, $v_t$ che ne rappresenta la velocità, e $i_t$ che ne rappresenta lo stato corrente del traffico attorno al veicolo.

Dato che conosciamo le kinemtiche della guida, possiamo invertirle per capire quali sono le azioni che l’autista sta prenendo. Ad esempio, se la macchina si muove in maniera uniforme e rettilinea, sappiamo che l’accelerazione è zero (cioé che non è stata presa un’azione).

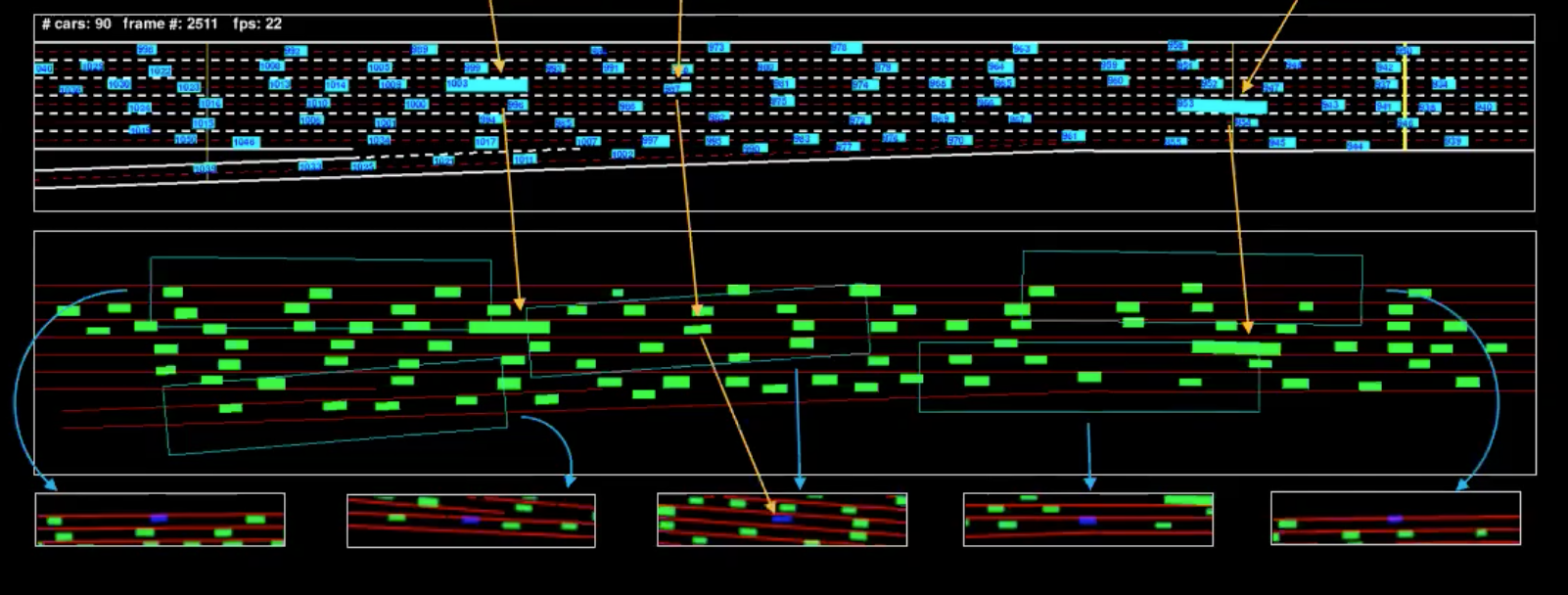
Fig. 4: Rappresentazione artificiale di un singolo frame

L’illustrazione in blu è il feed e l’illustrazione in verde è la cosiddetta rappresentazione artificiale (machine representation). Per capire meglio, abbiamo isolato un paio di veicoli (demarcati nell’illustrazione di sopra). Le visuali che vediamo di sotto sono le bounding box dei campi visivi di questi veicoli.

Costi

In questo caso abbiamo due tipi di costi diversi: il costo della corsia e il costo della prossimità. Il costo della corsia ci dice quanto siamo ben posizionati all’interno della corsia e il costo della prossimità ci dice quanto siamo vicini alle altre macchine.

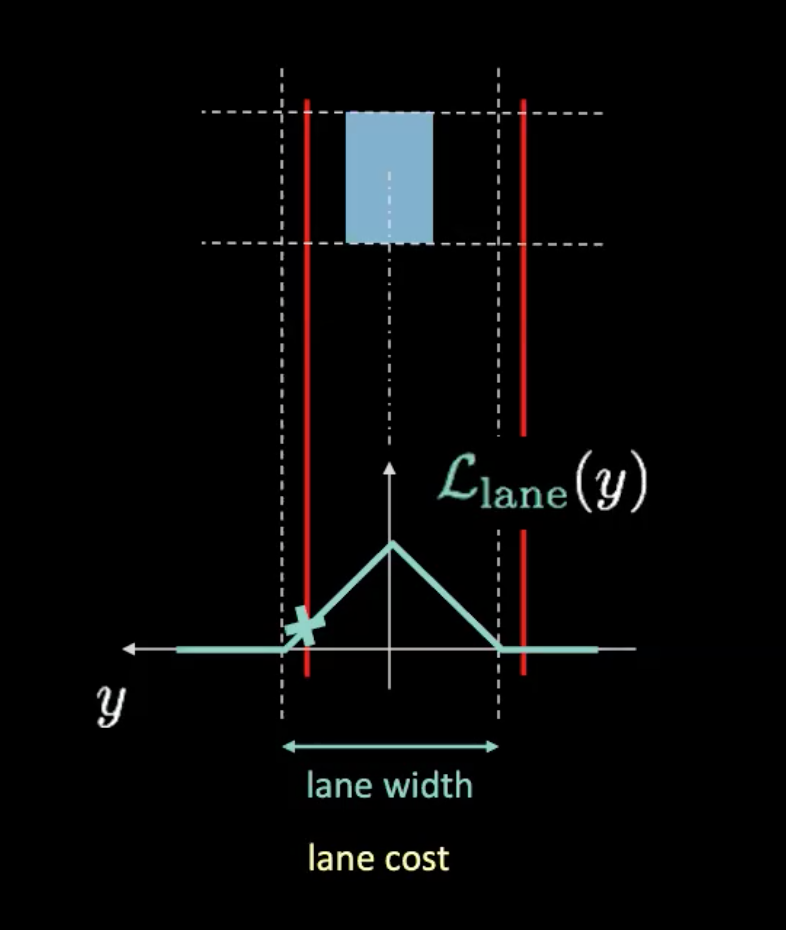
Fig. 5: Costo della corsia

Nella figura di sopra, le linee tratteggiate rappresentano il confine reale delle corsie, mentre le linee rosse indicano il costo della corsia data la posizione attuale della macchina. Le linee rosse si spostano con gli spostamenti della macchina. Il costo è dato dall’altezza dell’intersezione fra le linee rosse e la potenziale curva (in azzurro). Se la macchina è posizionata al centro della corsia, entrambi le linee rosse rientreranno nel confine della corsia, risultando in un costo uguale a zero. Se, invece, la macchina si allontana dal centro della corsia, le linee rosse si sposteranno con essa, risultando in un costo maggiore di zero.

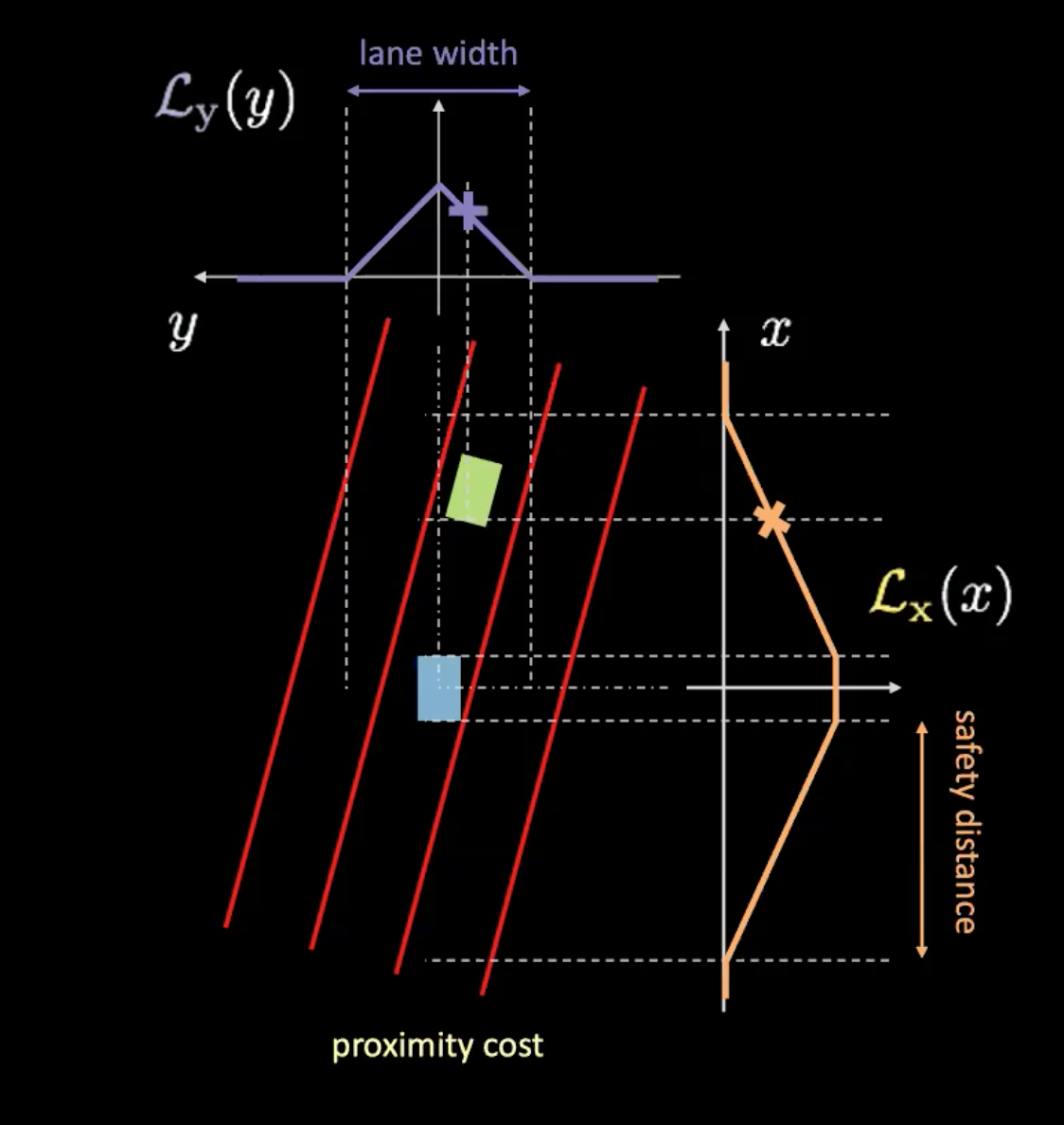
Fig. 6: Costo della prossimità

Il costo della prossimità ha a sua volta due componenti ($\mathcal{L}_x$ e $\mathcal{L}_y$). $\mathcal{L}_y$ è simile al costo della corsia e $\mathcal{L}_x$ dipende dalla velocità della nostra macchina. La curva arancione nella figura 6 rappresenta la distanza di sicurezza. Con l’aumentare della velocità della macchina, la curva arancione diventa più ampia. Quindi più velocemente cammina la macchina, più bisognerà guardarsi avanti e indietro. $\mathcal{L}_x$ rappresenta l’altezza dell’intersezione fra una macchina e la curva arancione.

Moltiplicando queste due componenti otteniamo il costo di prossimità.

Apprendimento di un modello della realtà

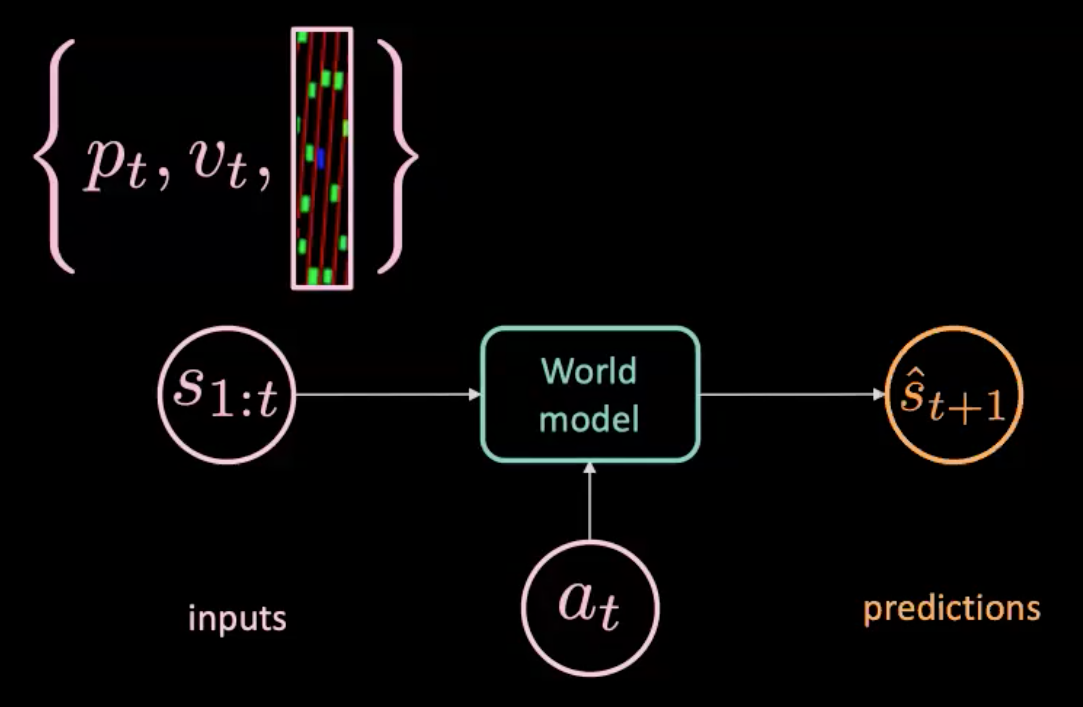
Fig. 7: Illustrazione del modello della realtà

Il modello della realtà prende come input un’azione $a_t$ (movimento del volante, freno, e accelerazione) e $s_{1:t}$ (la sequenza di stati, dove ogni stato viene rappresentato dalla posizione, la velocità, e le immagini del contesto in un determinato momento) e fa una previsione sul prossimo stato $\hat s_{t+1}$. Poi, osserviamo ciò che avviene realmente ($s_{t+1}$). Ottimizziamo l’errore quadratico medio fra ciò che il modello ha previsto ($\hat s_{t+1}$) ed il target, ovvero ciò che è accaduto realmente ($s_{t+1}$) ed addestriamo così il modello.

Previsore-decodificatore deterministico

Un modo per addestrare il modello della realtà è quello di usare un modello “previsore-decodificatore” (predictor-decoder model), che adesso spiegheremo.

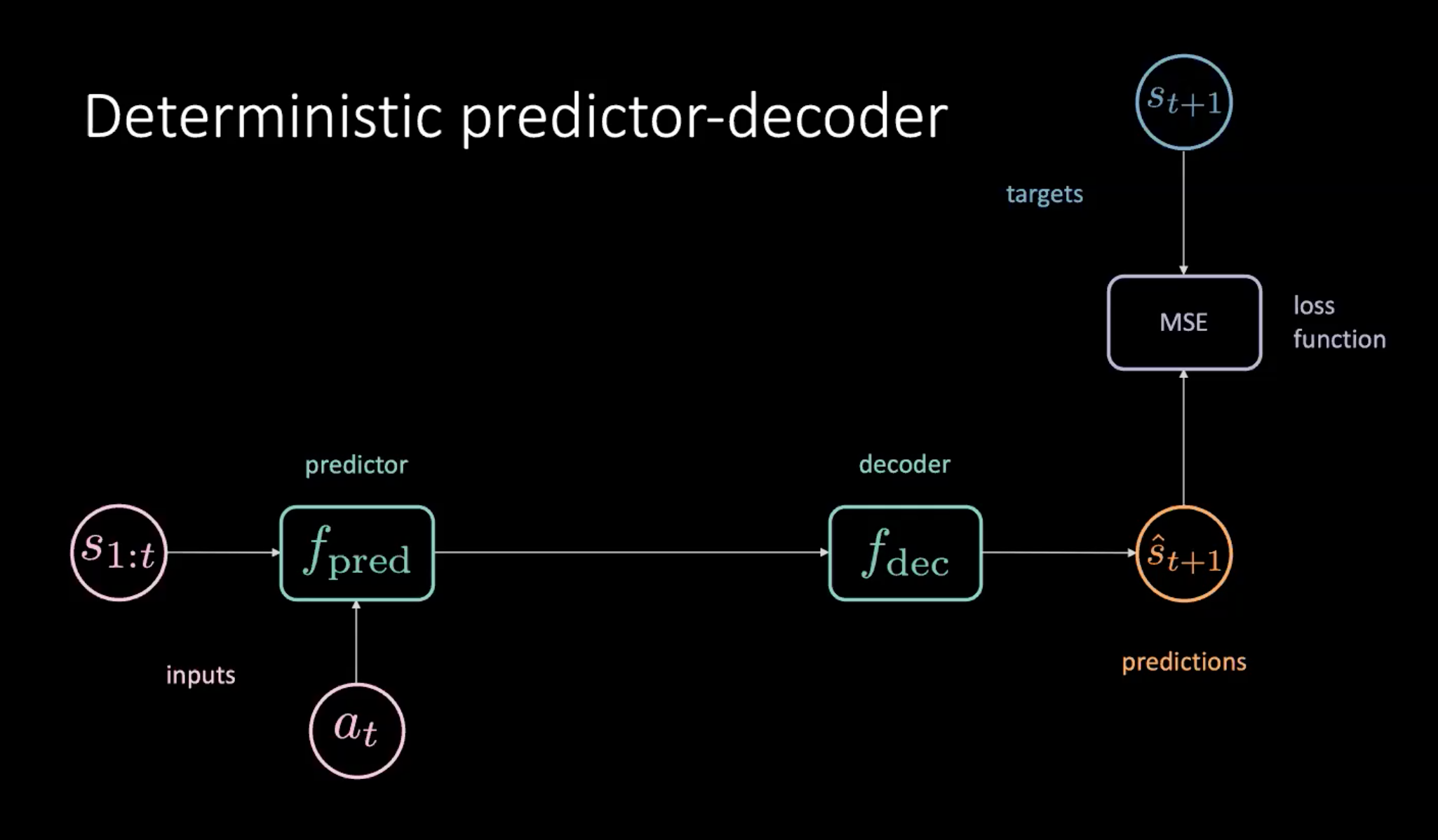
Fig. 8: Previsore-decodificatore deterministico per apprendere il modello della realtà

Come illustrato nella Fig. 8, abbiamo una sequenza di stati ($s_{1:t}$) e azioni ($a_t$) che vengono date come input al “previsore” (predictor module). Il previsore genera come output una rappresentazione nascosta del futuro, che viene data come input al decodificatore. Questo decodifica la rappresentazione nascosta del futuro e genera una previsione ($\hat s_{t+1}$). Poi addestriamo il modello minimizzando l’errore quadratico medio fra la previsione $\hat s_{t+1}$ e il target $s_{t+1}$.

Fig. 9: Futuro reale vs. future deterministco

Purtroppo, questo non funziona!

Possiamo vedere che l’output deterministico non è molto chiaro, perché il modello prende la media su tutte le possibilità future. Questo è paragonabile alla multi-modalità del futuro di cui abbiamo parlato qualche lezione fa, in cui abbiamo immaginato di far cadere una penna a caso dal centro. Prendendo la media su tutte le possibili posizioni in cui la penna potrebbe cadere finiremo per concludere che la penna non si è spostata affatto, il che sarebbe un errore.

Possiamo risolvere questo problema introducendo delle variabili latenti nel nostro modello.

Rete di previsione variazionale

Al fine di risolvere il problema che abbiamo discusso nella sezione precedente, aggiungiamo una variabile latente a bassa dimensionalità $z_t$ alla rete originale, che passa tramite un module di “espansione” $f_{exp}$ che fa corrispondere le dimensionalità.

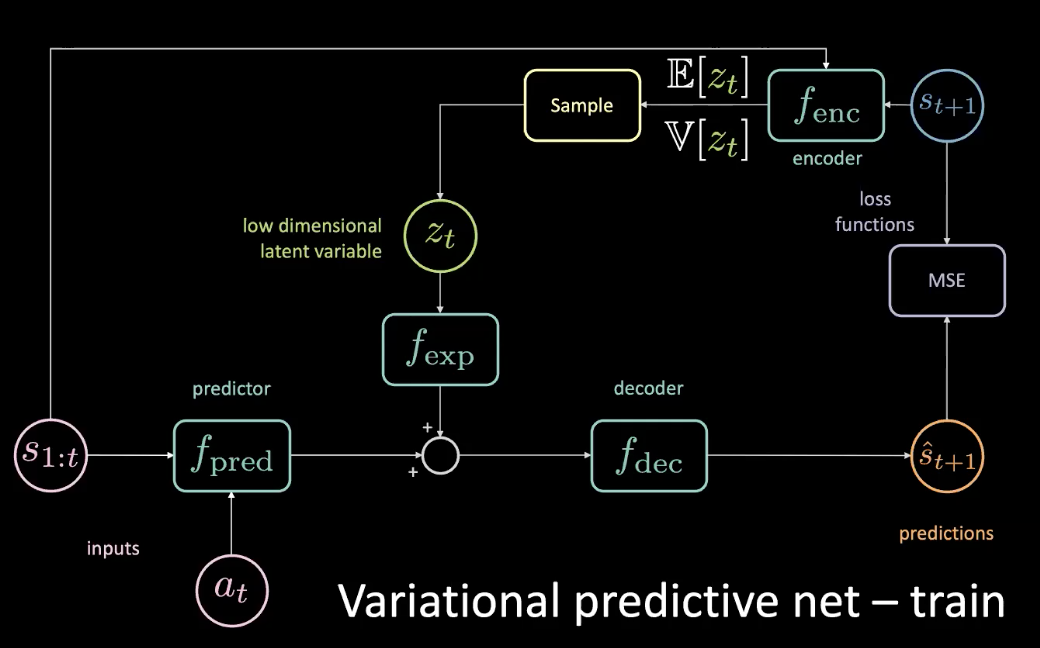
Fig. 10: Rete di previsione variazionale - addestramento

La $z_t$ viene scelta in modo da minimizzare l’errore quadratico medio per una previsione specifica. Regolando la variabile latente, possiamo comunque raggiungere un errore quadratico medio di zero tramite la discesa del gradiente sullo spazio latente. Fare questo però è molto costoso. Invece, possiamo predire la variabile latente utilizzando un codificatore. Il codificatore utilizza lo stato futuro per generare una distribuzione con una media e una varianza dalla quale possiamo campionare $z_t$.

Durante la fase di addestramento, possiamo vedere cosa accade guardando il futuro e raccogliendo informazioni che utilizzeremo per predire la variabile latente. Tuttavia, non abbiamo accesso al futuro durante la fase di test. Possiamo risolvere questo problema costringendo il codificatore a generare una distribuzione a posteriori che sia il più possibilmente simile alla distribuzione a priori, ottimizzando la divergenza di Kullback-Leibler (KL).

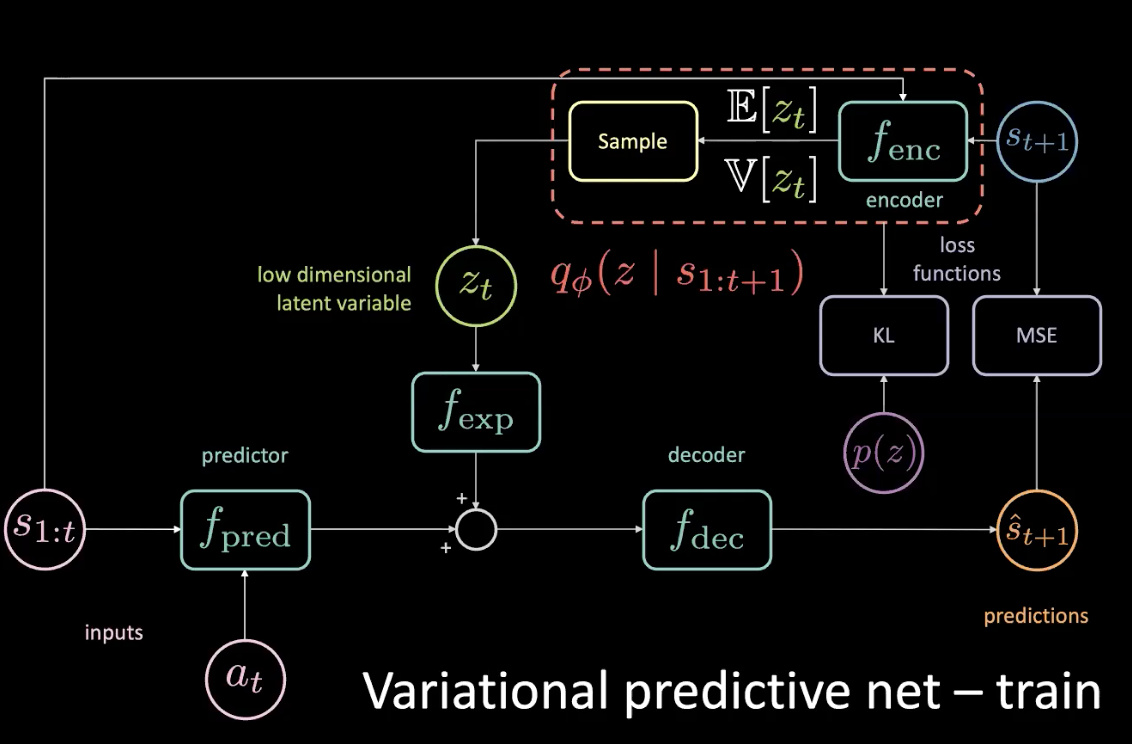
Fig. 11: Rete di previsione variazionale - addestramento (con distribuzione a priori)

Ora, vediamo la fase d’inferenza - come facciamo a guidare?

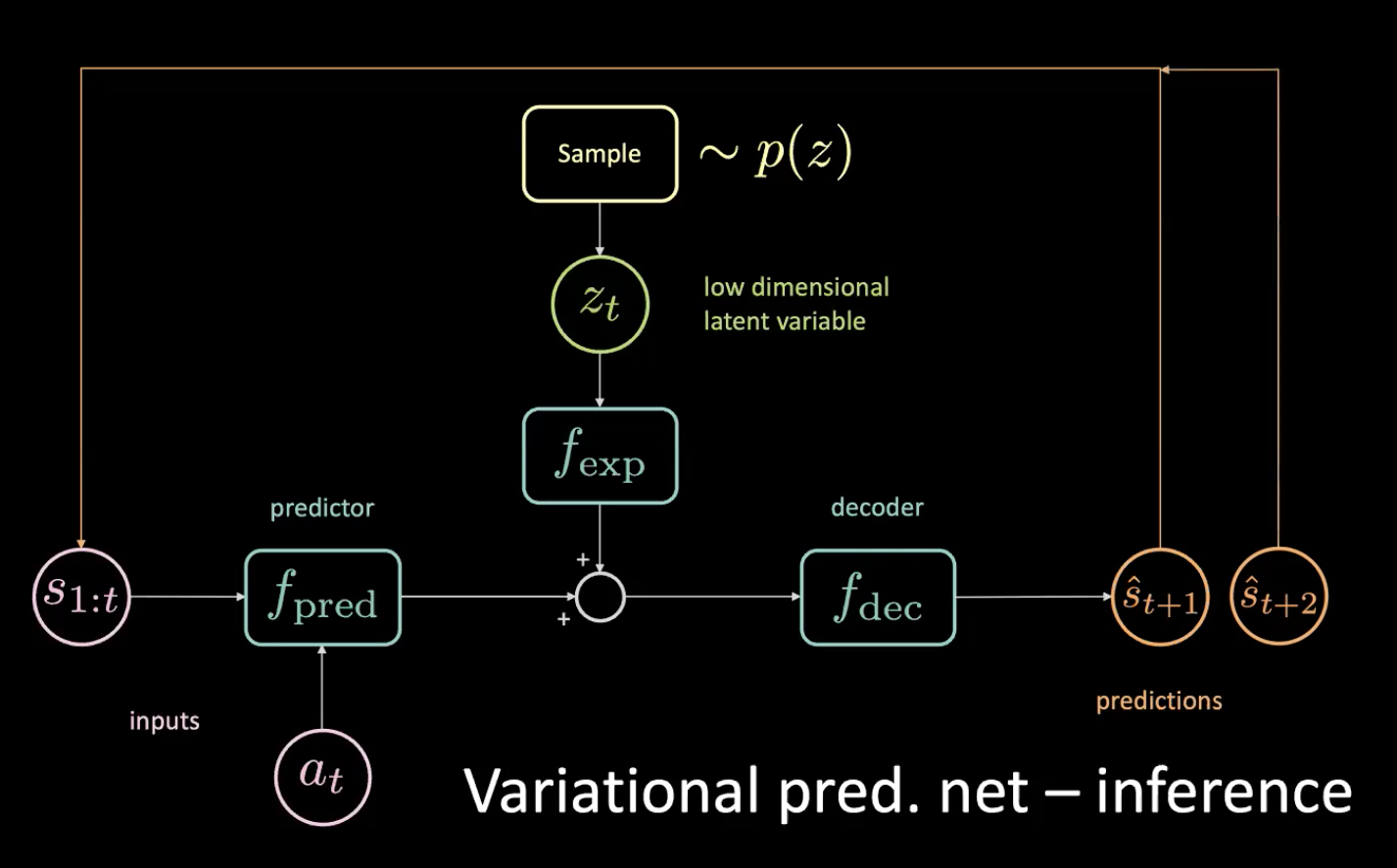
Fig. 12: Rete di previsione variazionale - inferenza

Campioniamo la variabile latente a bassa dimensionalità $z_t$ dalla distribuzione a priori costringendo il codificatore a renderla simile a questa distribuzione. Dopo aver fatto la previsione $\hat s_{t+1}$, la rimettiamo (tramite un processo auto-regressivo) ed otteniamo la prossima previsione $\hat s_{t+2}$, e continuiamo ad alimentare la rete così.

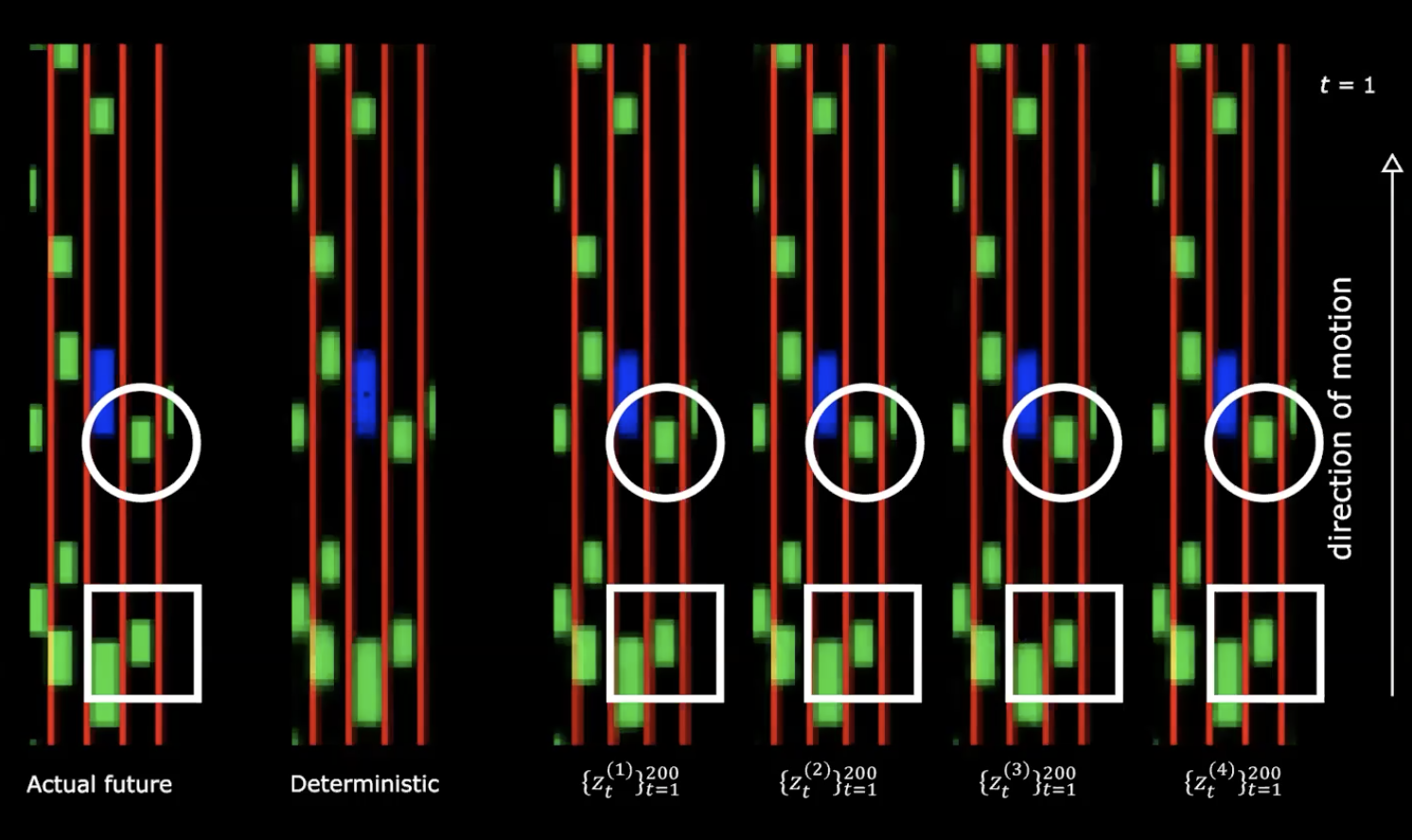
Fig. 13: Futuro reale vs. futuro deterministco

Sul lato destro della figura di sopra, vediamo quattro diversi campionamenti dalla distribuzione normale. Cominciamo con lo stesso stato iniziale e fornire 200 valori diversi della variabile latente.

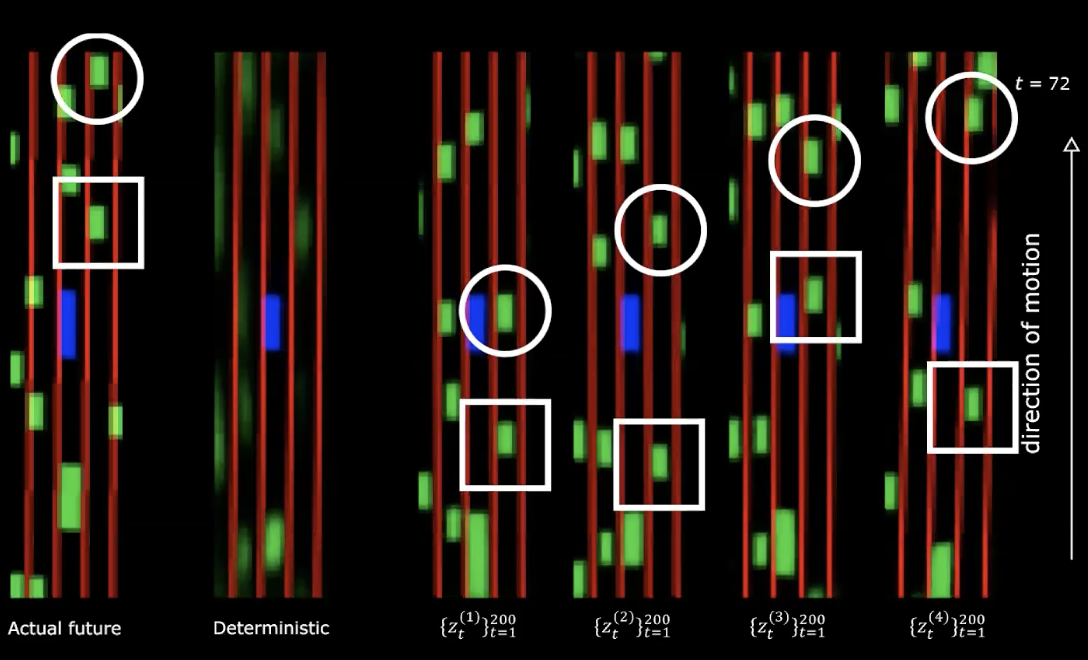
Fig. 14: Futuro reale vs. futuro deterministico - dopo un movimento

Possiamo notare che se forniamo diverse variabili latenti generiamo diverse sequenze di stati con comportamenti diversi. Questo significa che abbiamo una rete che genera il futuro. Piuttosto affascinante!

Cos’altro bisogna fare?

Ora possiamo utilizzare questa grande quantità di dati per addestrare la nostra politica ottimizzando i costi di corsia e di prossimità di cui abbiamo parlato precedentemente.

Questi molteplici futuri provengono dalla sequenza di variabili latenti che diamo come input alla rete. L’ascesa del gradiente - ovvero, provare ad aumentare il costo di prossimità nello spazio latente - ci permette di ottenere la sequenza di varibili latenti secondo le quali ci potremmo scontrare con le altre macchine.

Insensibilità alle azioni e dropout latente

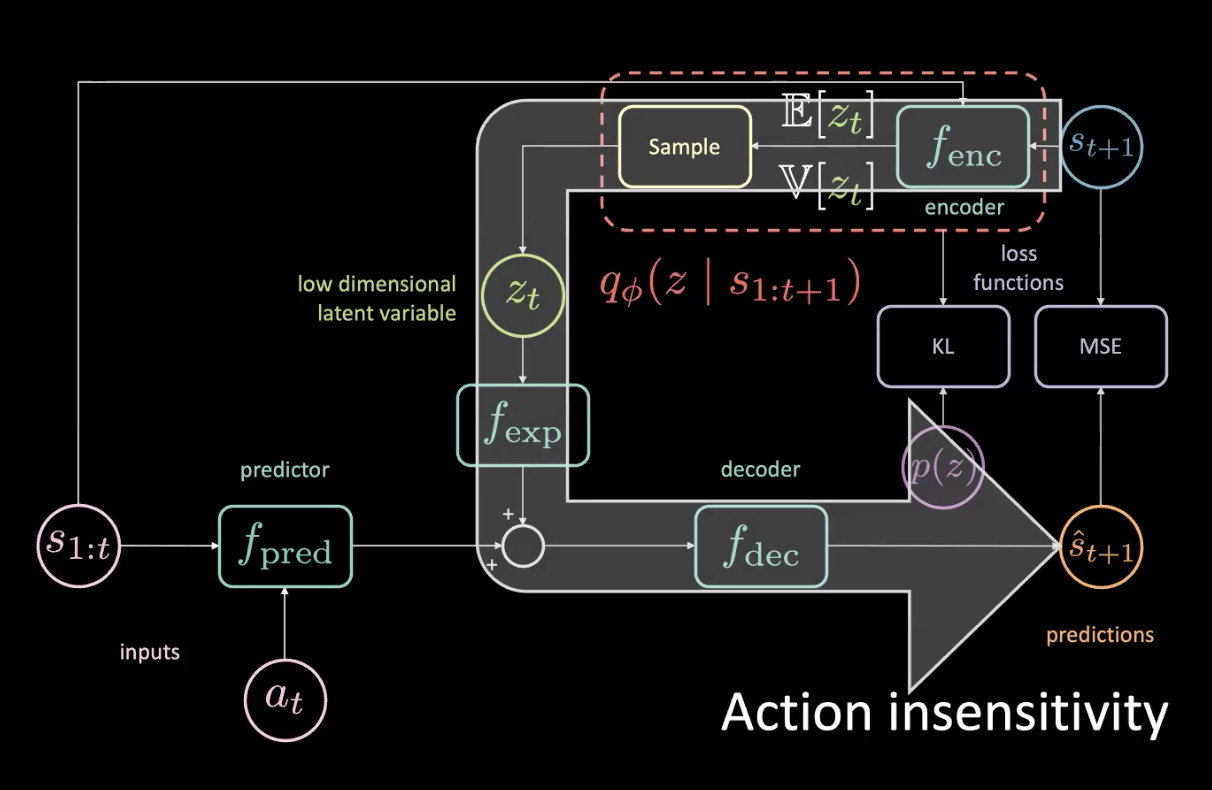
Fig. 15: Problemi - Insensibilità alle azioni

Dato che abbiamo accesso al futuro, se giriamo verso sinistra anche lievemente, l’ambiente circondante si sposterà alla nostra destra e questo contribuirà enormemente all’errore quadratico medio (mean squared error, MSE). La perdita MSE viene minimizzata quando la variabile latente riesce ad “informare” la base della rete che tutto verrà spostato sulla nostra destra - che non è ciò che vorremmo! Possiamo capire quando tutto girerà verso destra perché questa è un’operazione deterministica.

La freccia grossa nella Fig. 15 rappresenta una fuoriuscita (leak) d’informazione. Quindi la rete non è più sensibile all’azione corrente che viene data al previsore.

Fig. 16: Problema - Insensibilità alle azioni

Nella Fig. 16, nel diagramma più a destra abbiamo la vera sequenza di variabili latenti (le variabili latenti che ci permettono di ottenere il futuro più preciso) e non abbiamo la vera sequenza di azioni prese dall’esperto. Le due figure alla sinistra di questa mostrano un campionamento di una variabile latente e la vera sequenza di azioni, quindi ci aspettiamo di vedere un cambiamento di direzione. La figura più a sinistra ha la vera sequenza di variabili latenti ma con azioni arbitrarie. Si viede chiaramente che il cambio di direzione è dovuto più alla variabile latente che all’azione, che codificano la rotazione e l’azione (campionati da altri episodi).

Come risolvere questo problema?

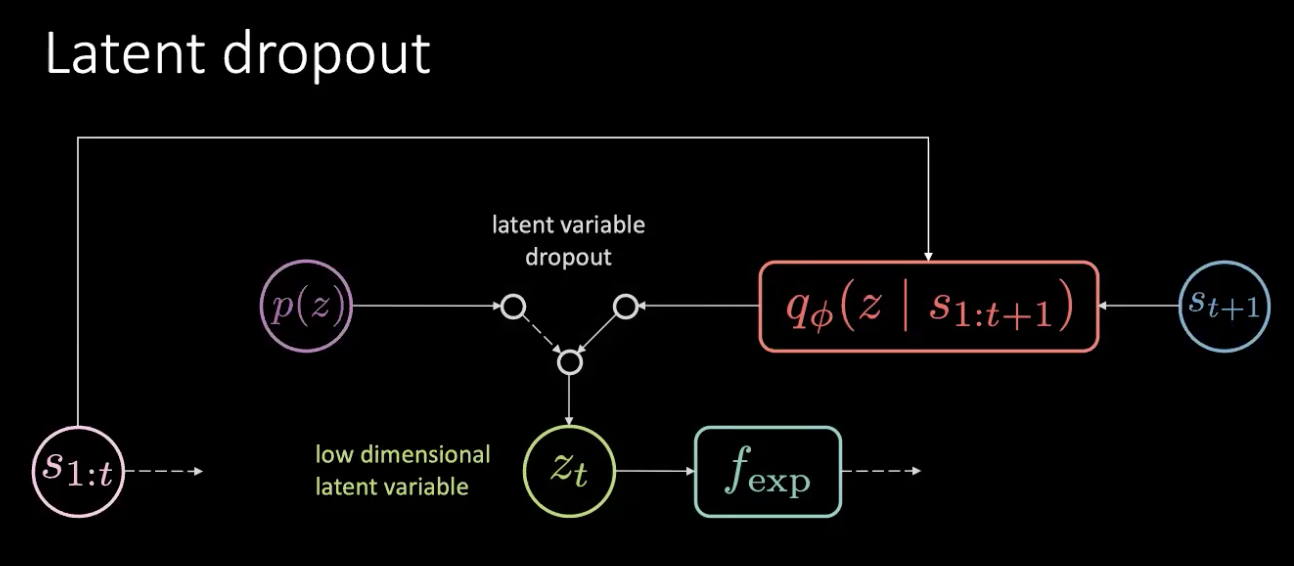
Fig. 17: Soluzione - eliminare la variabile latente

Il problema non è necessariamente un problema di fuoriuscita di memoria ma di fuoriuscita d’informazione. Lo risolviamo eliminando la variabile latente, campionandola invece dalla distribuzione a priori. Non abbiamo bisogno dell’output dell’encoder ($f_{enc}$) ma scegliamo dalla distribuzione a priori. Così facendo, non è più possibile codificare la rotazione nella variabile latente. Quindi, l’informazione viene codificata nell’azione piuttosto che nella variabile latente.

Fig. 18: Performance eliminando la variabile latente

Nelle ultime due immagini a destra, vediamo due diversi insiemi di variabili latenti, che hanno una vera sequenza di azioni e queste reti sono state addestrate con il “trucco” dell’eliminazione della variabile latente. Ora vediamo che la rotazione viene codificata nell’azione e non più dalla variabile latente.

Addestrare l’agente

Nelle sezioni precedenti, abbiamo visto come ottenere un modello della realtà simulando le esperienze reali. In questa sezione, utilizzeremo questo modello della realtà per addestrare il nostro agente. Il nostro obiettivo è quello di imparare la politica per prendere un’azione data ka storia degli stati precedenti. Dato uno stato $s_t$ (velocità, posizione & immagini di contesto), l’agente prenderà un’azione $a_t$ (accelerazione, freni & movimento del volante), il modello della realtà genererà un nuovo stato ed un costo ad esso associato $(s_t, a_t)$, che è una combinazione del costo di prossimità (proximity) ed il costo di corsia (lane).

Come discusso nelle sezioni precedenti, per evitare previsioni sfocate, dobbiamo campionare la variabile latenti $z_t$ dall’encoder dello stato futuro $s_{t+1}$ oppure dalla distribuzione a priori $P(z)$. Il modello della realtà prende come input gli stati precedenti $s_{1:t}$, le azioni prese dal nostro agente, e le variabile latente $z_t$ per predire lo stato successivo $\hat s_{t+1}$ and the cost. Questo costituisce un modulo che viene replicato diverse volte (Fig. 19) per darci una previsione finale e una perdita su cui ottimizzare.

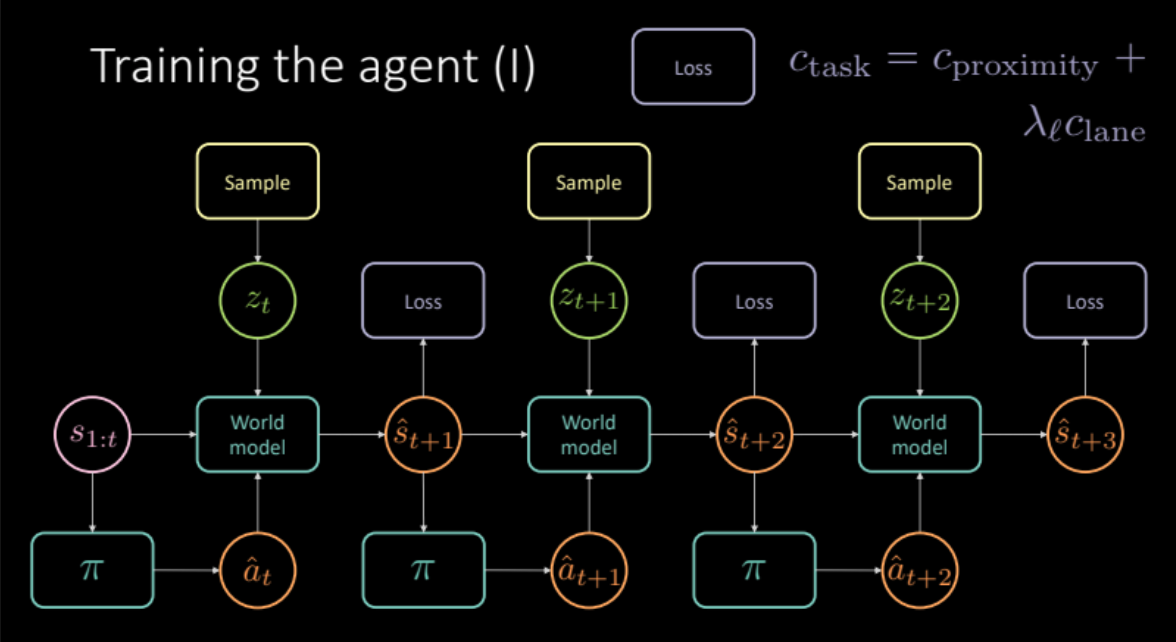
Fig. 19: Architettura del modello "specifico al compito"

Adesso che abbiamo il modello pronto, vediamo come funziona !!

Fig. 20: Politica appredsa: l'agente si scontra oppure si allontana dalla strada

Purtroppo, non funziona. Le politiche addestrate in questo modo non sono utili in quanto apprendono a predire tutto nero dato che questo risulta in un costo uguale a zero.

Come possiamo risolvere questo problema? Possiamo provare ad imitare altri veicoli per migliorare le nostre previsioni?

Imitando l’esperto

Come facciamo ad imitare gli esperti qui? Vogliamo che la previsione del nostro modello dopo aver preso una particolare azione da uno stato sia il più vicino possibile al futuro reale. Questo si comporta come un agente esperto che regolarizza la nostra fase di addestramento. La nostra funzione di costo ora include sia il costo per questo compito (task) specifico (ovvero i costi di prossimità e corsia) ma anche questo termine del “regolarizzatore esperto” (expert regulariser). Ora, dato che calcoliamo anche la perdita rispetto al futuro reale, dobbiamo rimuovere le variabili latenti dal modello perché questo ci da una previsione specifica, ma questo contesto funziona meglio se utilizziamo la previsione media.

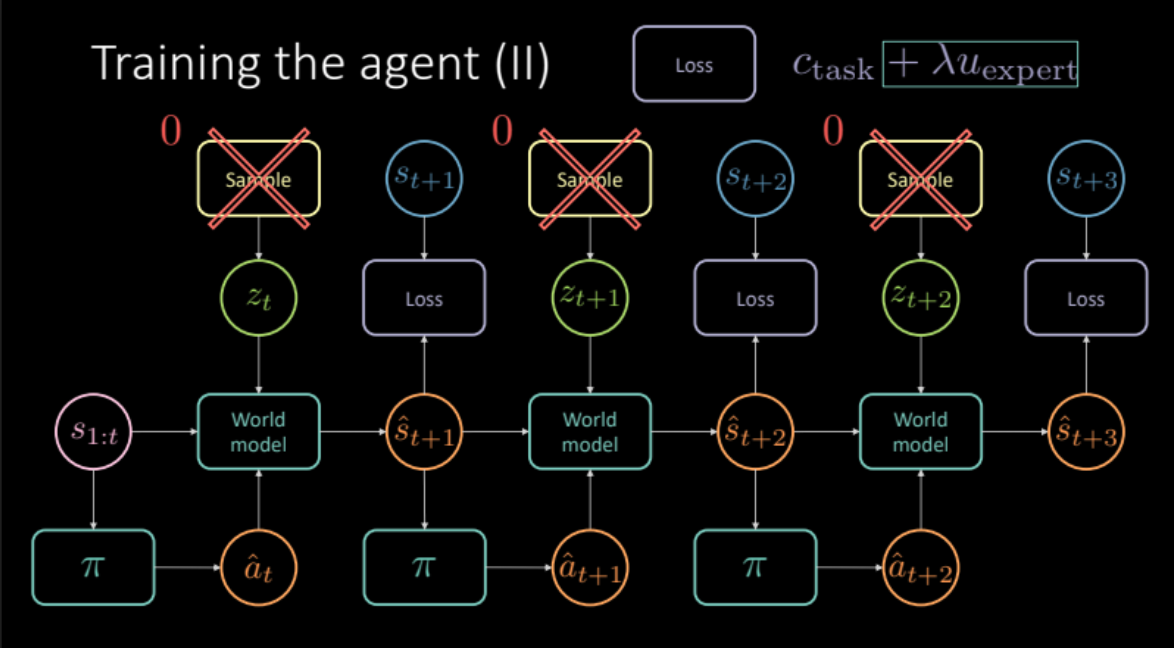
Fig. 21: Architettura del modello basato sull'imitazione degli esperti

Quindi quanto funziona bene questo modello?

Fig. 22: Politica appresa sulla base dell'imitazione degli esperti

Come vediamo nella figura di sopra, il modello funziona incredibilmente bene ed impara a fare previsioni molto buone. Questo è un modello basato sull’apprendimento tramite l’imitazione, abbiamo provato a modellare in modo che l’agente provi ad imitare gli altri.

Ma possiamo fare di meglio? Abbiamo addestrato l’autoencoder variazionale per poi rimuoverlo alla fine?

Fatto sta che possiamo migliorare ancora di più se cerchiamo di minimizzare l’incertezza delle previsioni forward del modello.

Minimizzare l’incertezza del modello

Cosa s’intende per minimizzare l’incertezza (uncertainty) delle previsioni forward del modello, e come lo si fa? Prima di rispondere a questo domdada, ripassiamo un concetto che abbiamo visto nella pratica della terza settimana.

Se addestriamo più di un modello sugli stessi dati, tutti i modelli devono concordare sui punti nella regione di addestramento (mostrati in rosso), che risulta in varianza zero nella regione di addestramento. Spostandoci più lontano dalla regione di addestramento, le traiettorie della perdita di questi modelli cominciano a divergere e la varianza aumenta. Questo viene illustrato nella figura 23. Dato che la varianza è differenziabile, possiamo utilizzare la discesa del gradiente sulla varianza per minimizzarla.

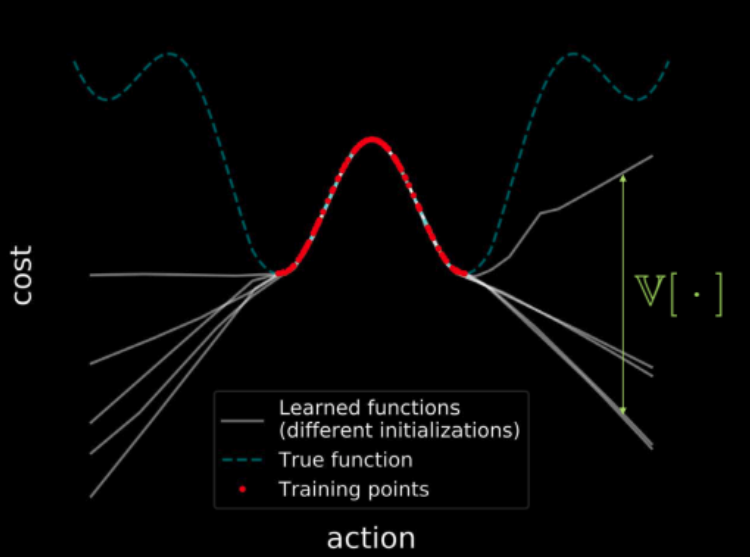
Fig. 23: Visualizzazione del costo attraverso l'intero spazio d'input

Tornando alla nostra discussione, osserviamo che imparare una politica utilizzando solo dati osservati è difficile perché la distribuzione di stati che produce al momento di esecuzione può essere diverso da quello che osserviamo durante la fase di addestramento. Il modello della realtà può fare previsioni arbitrarie che stanno al di fuori degli esempi su cui è stato addestrato, che potrebbe essere associato (erroneamente) ad un costo basso. La rete a politiche potrebbe sfruttare questi errori nel modello dinamico e produrre azioni che portano a stati erroneamente ottimistici.

Per evitare questo problema, proponiamo un costo addizionale, che misura l’incertezza sul modello dinamico rispetto alle proprie previsioni. Questo può essere calcolato dando lo stesso input e azione a tante diverse “maschere” di dropout, e calcolando poi la varianza sui diversi outputs. Questo incoraggia alla rete di politiche di produrre solo azioni di cui il modello forward è “convinto”.

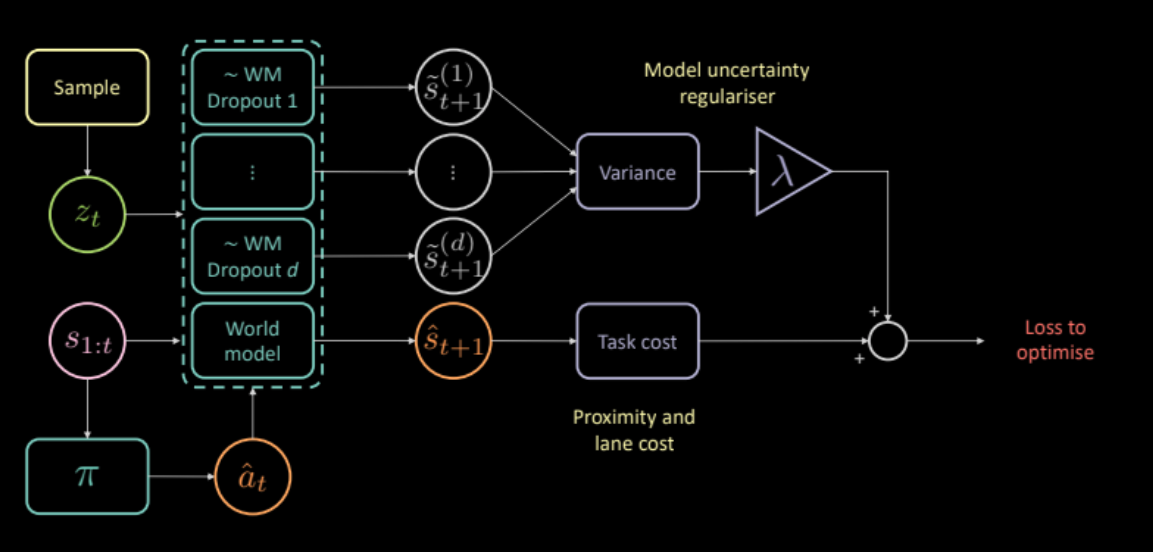
Fig. 24: Architettura del modello basato sul regolarizzatore dell'incertezza

Quindi, il regolarizzatore dell’incertezza ci aiuta ad apprendere una politica migliore?

Sì, la politica appresa tramite questo metodo è meglio di quelle dei modelli precedenti.

Fig. 25: Politica appresa sulla base del regolarizzatore dell'incertezza

Valutazione

La Fig. 26 dimostra quanto bene ha imparato il nostro agente a guidare nel traffico. La macchina gialla è l’autista originale,la macchina blu è l’agente appreso, e tutte le macchine verdi vengono “occluse” (non posso essere controllate).

Fig. 26: Performance del modello con regolarizzatore dell'incertezza