Funzioni di perdita (cont.) e funzioni di perdita per i modelli ad energia

🎙️ Yann LeCun

Perdita ad entropia incrociata binaria - nn.BCELoss()

$\ell(x,y) = L = \{l_1,...,l_N\}^T, \qquad l_n = -w_n[y_n\log x_n+(1-y_n)\log(1-x_n)]$

Questa perdita è un esempio speciale della funzione di entropia incrociata binaria (binary cross entropy, BCE), che ci permette di semplificare la funzione quando si hanno solo due categorie. Questa viene utilizzata per misurare l’errore di una ricostruzione, come ad esempio per un autoencoder. La formula presuppone che $x$ e $y$ siano probabilità, e quindi che prendano valori fra 0 ed 1.

Perdita di divergenza Kullback-Leibler - nn.KLDivLoss()

$\ell(x,y) = L = \{l_1,...,l_N\}^T, \qquad l_n = y_n(\log y_n-x_n)$

Questa è una semplice funzione di perdita per quando la target segue una distribuzione one-hot (i.e. $y$ è una variabile categorica). Come nella funzione di perdita BCE, presupponiamo che i valori di $x$ e $y$ rappresentino probabilità. Questo ha lo svantaggio che, se la funzione non viene affiancata ad una funzione di softmax o log-softmax potrebbero sorgere problematiche di stabilità numerica.

Perdita BCE con Logit - nn.BCEWithLogitsLoss()

$\ell(x,y) = L = \{l_1,...,l_N\}^T, \qquad l_n = -w_n[y_n\log \sigma(x_n)+(1-y_n)\log(1-\sigma(x_n))]$

Questa versione di perdita ad entropia incrociata binaria prende come input dei punteggi ai quali non è stata applicata la funzione di softmax (e quindi non presuppone che il valore dell’input $x$ sia compreso fra 0 ed 1). Questi vengono passati ad una funzione sigmoide, che garantisce che i valori di output siano compresi fra 0 e 1. Combinando le funzioni di perdita in questo modo aumenta la probabilità che la perdita sia stabile numericamente.

Perdita a classifica di margine - nn.MarginRankingLoss()

$L(x,y) = \max(0, -y*(x_1-x_2)+\text{margine})$

Le perdite a margine costituiscono una categoria importante fra le funzioni di perdita. Se si hanno due input, questa funzione di perdita fa si che un input sia più grande dell’altro di almeno un margine. In questo caso $y$ è una variabile binaria $\in { -1, 1}$. Immaginiamo che i due input siano i punteggi di due categorie: vogliamo che il punteggio per la categoria corretta sia maggiore del punteggio per la categoria sbagliata di almeno un margine. Come nella funzione di perdita hinge, se $y*(x_1-x_2)$ è maggiore del margine, il costo è uguale a 0. Se è minore, il costo aumenta linearmente. Se dovessimo usare questa funzione di perdita per la classificazione, dovremmo avere $x_1$ come punteggio della categoria corretta e $x_2$ come punteggio maggiore fra le categorie sbagliate nel mini-batch. Se utilizzata in un modello ad energia, (di cui discuteremo successivamente), questa funzione di perdita “spingerà verso il basso” (assegnando cosí un valore di energia minore) la risposta corretta $x_1$ e “spingerà verso l’alto” (assegnando cosí un valore di energia maggiore) la risposta sbagliata $x_2$.

Perdita a margini a triade - nn.TripletMarginLoss()

$L(a,p,n) = \max\{d(a_i,p_i)-d(a_i,n_i)+\text{margine}, 0\}$

Questa perdita viene utilizzata per misurare la similitudine relativa fra esempi. Ad esempio, se passiamo due immagini della stessa categoria ad una CNN e ottieniamo due vettori, vorremmo che la distanza fra due vettori sia la minore possibile. Se invece abbiamo due immagini con categorie diverse, vorremmo che la distanza fra i due vettori sia la maggiore possibile. Questa funzione di perdita spinge verso zero la distanza fra vettori rappresentanti la stessa categoria, e spinge oltre un determinato margine la distanza fra due vettori rappresentanti categorie diverse. Tuttavia, l’unica cosa che importa è che la distanza fra le coppie “giuste” sia minore della distanza fra le coppie “sbagliate”.

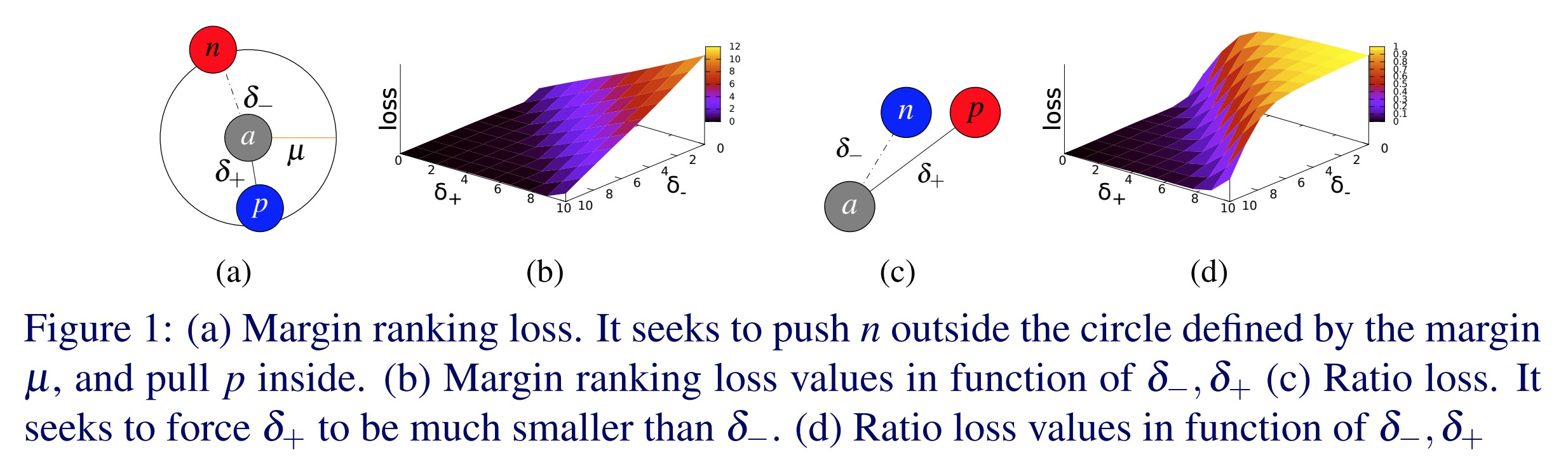
Fig. 1: Perdita a margini a triade

Questa perdita venne utilizzata originariamente per addestrare un sistema di ricerca di immagini per Google. Digitando una ricerca su Google, il sistema la codifica come vettore, che poi viene paragonato ad altri vettori di immagini già identificate. Google ripesca quelle immagini i cui vettori hanno la distanza minore dal vettore di input.

Perdita a margine morbido - nn.SoftMarginLoss()

$L(x,y) = \sum_i\frac{\log(1+\exp(-y[i]*x[i]))}{x.\text{nElement()}}$

Questa funziona crea un criterio che ottimizza un sistema di classificazione logistica a due classi tra un tensore di input $x$ e un tensore di target $y$ (contenente valori uguali a 1 o -1).

• Questa è la versione softmax di una perdita a margine. Si hanno vari esempi positivi ed esempi negativi da passare tramite il softmax. La funzione poi prova a rendere $\text{exp}(-y[i]*x[i])$ per il valore corretto di $x[i]$ minore di qualunque altro.
• Questa funzione di perdita “ravvicina” i valori positivi di $y[i]*x[i]$ e “spinge” i valori negative ad essere lontani l’uno dall’altro. Al contrario di un margine “duro”, questa funziona ha un effetto continuo sulla perdita, che diminuisce in maniera esponenziale.

Perdita hinge per molteplici categorie - nn.MultiLabelMarginLoss()

$L(x,y)=\sum_{ij}\frac{max(0,1-(x[y[j]]-x[i]))}{x.\text{dimensione}(0)}$

Questa funzione a margine permette a diversi input di avere un numero variabile di output. In questo caso abbiamo diverse categorie per le quali vorremmo dei punteggi alti, e prendiamo la somma della funzione di perdita hinge su tutte le categorie. Per gli EBM, questa funzione di perdita spinge verso il basso le categorie desiderate, e spinge verso l’alto quelle non desiderate.

Perdita di hinge ad immersione - nn.HingeEmbeddingLoss()

$l_n = \left\{ \begin{array}{lr} x_n, &\quad y_n=1, \\ \max\{0,\Delta-x_n\}, &\quad y_n=-1 \\ \end{array} \right.$

La perdita di Hinge ad immersione viene utilizzata per l’apprendimento semi-supervisionato (semi-supervised learning) attraverso una misura della somiglianza fra due input. Questa funziona “ravvicina” gli esempi simili e allontana gli esempi dissimili l’uno dall’altro. La variabile $y$ ci indica la direzione (ravvicinamento vs. allontanamento) del punteggio per una coppia di input. Utilizzando una perdita hinge, il punteggio è positivo se $y$ è uguale a 1 ed è uguale ad un margine $\Delta$ se $y$ è uguale a -1.

Perdita di coseno ad immersione - nn.CosineEmbeddingLoss()

$l_n = \left\{ \begin{array}{lr} 1-\cos(x_1,x_2), & \quad y=1, \\ \max(0,\cos(x_1,x_2)-\text{margine}), & \quad y=-1 \end{array} \right.$

Questa funzione di perdita misura la somiglianza fra due input, utilizzando la distanza del coseno di similitudine, e viene tipicamente utilizzata per apprendere immersioni non-lineari o per l’apprendimento semi-supervisionato.

• Definito in maniera alternativa, 1 meno il coseno dell’angolo fra due vettori è praticamente la distanza Euclidea normalizzata.
• Il vantaggio di questa funzione è che quando si hanno due vettori e li si vuole rendere molto distanti fra di loro, lo si può ottenere semplicemente rendendo i vettori molto lunghi. Ovviamente questo non è ottimale, perché non vogliamo aumentare la lunghezza dei vettori ma ruotarli nella direzione giusta. Per questo, si normalizzano i vettori e si calcola la distanza Euclidea fra di loro.
• Per le coppie di vettori “positive” (appartenenti alla stessa categoria), questa perdita tenta di allineare i vettori fra di loro il più possibile. Per le coppie “negative” (appartenenti a categorie diverse), la perdita rende il coseno minore di un margine, che deve avere un valore basso ma positivo.
• In uno spazio ad alta dimensionalità, abbiamo una concentrazione alta di punti attorno all’“equatore” della sfera. Dopo aver normalizzato i vettori, tutti i punti si trovano distribuiti sulla sfera. Desideriamo che i punti semanticamente simili siano vicini. Gli esempi dissimili, invece, dovrebbero essere ortogonali. Non vogliamo che siano in direzione opposta perché vi è un solo punto al polo opposto . Dato che sull’“equatore” abbiamo una grande quantità di spazio, vorremmo avere un margine dal valore basso cosí da poter sfruttare tutta l’area in questa regione.

Perdita a classificazione temporale connettivista (Temporal Classification, CTC) - nn.CTCLoss()

Calcola la perdita fra una serie temporale continua (non segmentata) e una sequenza di target.

• La perdita CTC prende la somma sulle probabilità di diversi allineamenti fra la sequenza d’input e la sequenza di target. Questo produce un valore di perdita che è differenziabile rispetto a ciascun nodo di input.
• L’allineamnto dell’input e il target viene presunto essere “many-to-one” , il che limita la lunghezza della sequenza di target così da renderla minore o uguale alla lunghezza della sequenza d’input.
• Questa funzione di perdita è utile quando l’output è una sequqnza di vettori, che corrispondono a dei punteggi per ogni categoria.

Fig. 2: Perdita CTC per il riconoscimento vocale

Esempio di applicazione: sistema di riconoscimento vocale

• Obiettivo: predirre quale parola viene pronunciata ogni 10 millisecondi.
• Ciascuna parola viene rappresentata da una sequqnza di suoni.
• Dipende dalla velocità della parlata della persona, suoni di diversa lunghezza si possono mappare alla stessa parola.
• Bisogna trovare la mappatura migliore che collega la sequenza di input alla sequenza di output. Un buon metodo per ottenere questo è quello di utilizzare programmazione dinamica per trovare il cammino a costo minimo.

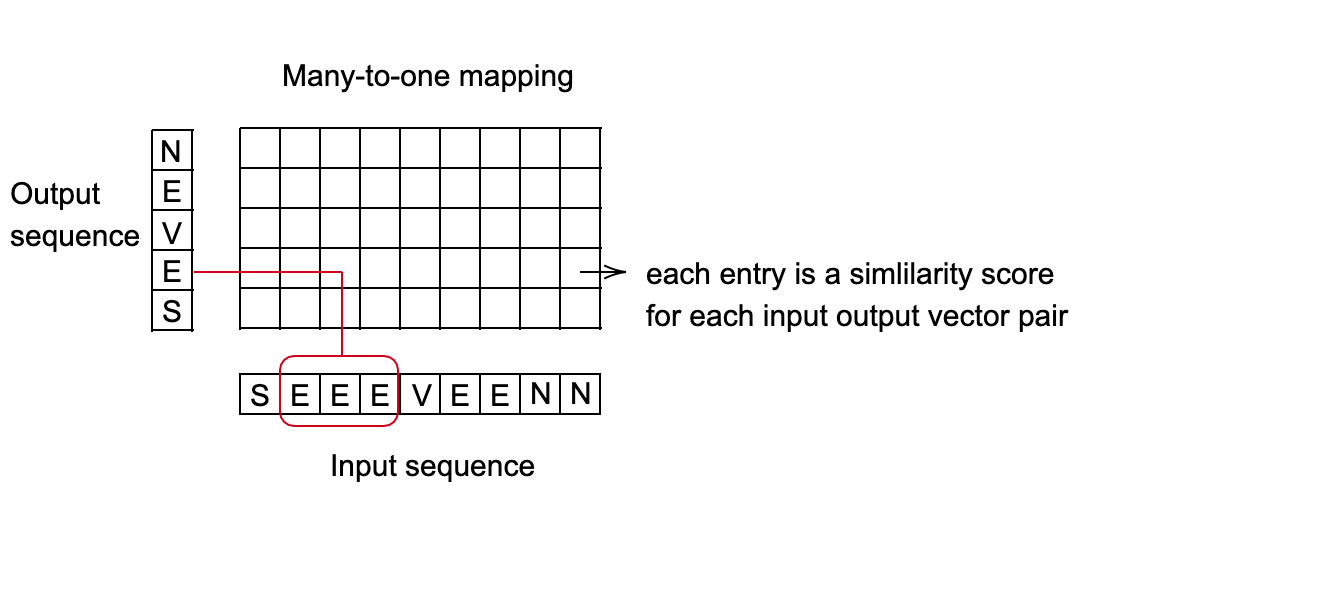
Fig. 3: Impostazione della mappatura "many-to-one"

Modelli ad energia (Parte IV) - Funzioni di perdita

Architetture e la funzione di perdita

Una famiglia di funzioni di energia: $\mathcal{E} = {E(W,Y, X) : W \in \mathcal{W}}$.

Dati di addestramento: $S = {(X^i, Y^i): i = 1 \cdots P}$

Funzionale di perdita: $\mathcal{L} (E, S)$

• Funzionale significa una funzione di un’altra funzione. Nel nostro caso, la funzionale $\mathcal{L} (E, S)$ è una funzione della funzione di energia $E$.
• Poiché $E$ è parametrizzata da $W$, possiamo trasformare il funzionale in una funzione di perdita $W$: $\mathcal{L} (W, S)$
• Qeusta misura la qualità della funzione di energia sui dati di addestramento.
• È invariante alle permutazioni e alle ripetizioni degli esempi.

Addestramento: $W^* = \min_{W\in \mathcal{W}} \mathcal{L}(W, S)$.

Forma della funzionale di perdita:

• $L(Y^i, E(W, \mathcal{Y}, X^i))$ è la perdita per-sample (per un singolo esempio).
• $Y^i$ è il valore di target, può essere una categoria, un’immagine, etc.
• $E(W, \mathcal{Y}, X^i)$ è la superficie di energia per un determinato $X_i$ con il variare di $Y$.
• $R(W)$ è la regolarizzazione

$\mathcal{L}(E, S) = \frac{1}{P} \sum_{i=1}^P L(Y^i, E(W,\mathcal{Y}, X^i)) + R(W)$

Definire una buona funzione di perdita

Abbassare l’energia degli esempi corretti.

Aumentare l’energia sugli esempi sbagliati, in particolare se hanno energia minore degli esempi corretti.

Esempi di una funziona di perdita

Perdita ad energia

$L_{energia} (Y^i, E(W, \mathcal{Y}, X^i)) = E(W, Y^i, X^i)$

Questa funzione di perdita semplicemente riduce il valore di energia per gli esempi corretti. Se la rete non è definita nella maniera giusta, può finire per avere una funziona di energia piuttosto piatta, poiché la funzione di perdita riduce l’energia degli esempi corretti senza però aumentare l’energia nelle altre regioni. Quindi, il sistema potrebbe crollare.

Perdita log-verosomiglianza negativa (negative log-likelihood, NLL)

$L_{NLL}(W, S) = \frac{1}{P} \sum_{i=1}^P (E(W, Y^i, X^i) + \frac{1}{\beta} \log \int_{y \in \mathcal{Y}} e^{\beta E(W, y, X^i)})$

Questa funzione di perdita ridue l’energia degli esempi corretti, aumentando l’energia di tutti gli altri esempi in maniera proporzionale alla loro probabilità. Questo si riduce alla perdita percettrone (perceptron loss) quando $\beta \rightarrow \infty$. Questa funziona è stata utilizzata da molto tempo in diversi contesti per effettuare l’addestramento discriminativo (discriminative training) con output strutturati (structured outputs).

Un modello probabilistico è un EBM in cui:

• Si può prendere l’integrale rispetto ad Y di una funzione ad energia (la variabile da predire)
• La funzione di perdita è la funzione di log-verosomiglianza negativa.

Perdita percettrone

$L_{percettrone}(Y^i,E(W,\mathcal Y, X^*))=E(W,Y^i,X^i)-\min_{Y\in \mathcal Y} E(W,Y,X^i)$

Questa funzione di perdita è molto simile alla funzione di perdita del percettrone di più di 60 anni fa. La funzione è sempre positiva perché prende il minimo degli $Y^i$, quindi $E(W,Y^i,X^i)-\min_{Y\in\mathcal Y} E(W,Y,X^i)\geq E(W,Y^i,X^i)-E(W,Y^i,X^i)=0$. La stesso calcolo dimostra che la funzione è uguale a zero solo quando $Y^i$ è l’output giusto.

Questa perdita rende l’energia dell’esempio corretto molto bassa, allo stesso tempo facendo aumentare il più possibile l’energia di tutti gli altri esempi. Tuttavia, questa perdita non preclude che la funzione dia lo stesso valore a ciascun esempio sbagliato $Y^i$, quindi in un certo senso non è una buona perditaper sistemi non-lineari. Per migliorare questa perdita, definiamo il concetto di “errore più grave” (most offending incorrect answer, letteralmente: la risposta sbagliata più offensiva).

Perdita a margine generalizzato

Errore più grave: caso discreto Supponiamo che $Y$ sia una variabile discreta. Allora per un esempio di addestramento $(X^i,Y^i)$, l’errore più grave $\bar Y^i$ è quell’output che ha l’energia minore fra tutti i possibili output sbagliati:

$\bar Y^i=\text{argmin}_{y\in \mathcal Y\text{ e }Y\neq Y^i} E(W, Y,X^i)$

Errore più grave: caso continuo Supponiamo che $Y$ sia una variabile continua. Allora per un esempio di addestramento $(X^i,Y^i)$, l’errore più grave $\bar Y^i$ è quell’output che ha l’energia minore fra tutti i possibili output sbagliati che sono almeno $\epsilon$ dall’output corretto:

$\bar Y^i=\text{argmin}_{Y\in \mathcal Y\text{ e }\|Y-Y^i\|>\epsilon} E(W,Y,X^i)$

Nel caso discreto, l’errore più grave è quello che ha il valore di energia minore che però non è l’output corretto. Nel caso continuo, l’energia per $Y$ nelle vicinanze di $Y^i$ dovrebbe essere approssimativamente $E(W,Y^i,X^i)$. Inoltre, l’$\text{argmin}$ preso sui valori di $Y$ non uguali a $Y^i$ sarebbe 0. Di consequenza, scegliamo una distanza $\epsilon$ e decidiamo che sono le $Y$ che sono almeno a $\epsilon$ di distanza da $Y_i$ possono essere considerate “errori”. Questo è il motivo per cui l’ottimizzazione si compie solo sulle $Y$ che sono almeno a $\epsilon$ di distanza da $Y^i$.

Se la funzione d’energia è in grado di fare sí che l’energia dell’“errore più grave” sia maggiore (di un determinato margine) dell’energia dell’esempio corretto, allora questa funzione di energia dovrebbe funzionare bene.

Esempi di funzioni di perdita a margine generalizzato

Perdita hinge

$L_{\text{hinge}}(W,Y^i,X^i)=( m + E(W,Y^i,X^i) - E(W,\bar Y^i,X^i) )^+$

Dove $\bar Y^i$ è l’“errore più grave”. Questa perdita fa sí che la differenza fra l’output giusto e l’errore più grave sia come minimo uguale a $m$.

Fig. 4: Perdita Hinge

Domanda: Come scegliamo $m$?

Risposta: È arbitrario, ma la scelta ha un effetto sui pesi dell’ultimo strato della rete. –>

Perdita Logaritmica (Log Loss)

$L_{\log}(W,Y^i,X^i)=\log(1+e^{E(W,Y^i,X^i)-E(W,\bar Y^i,X^i)})$

Si può pensare di questa funzione come una versione “morbida” della perdita hinge. Invece di calcolare la differenza fra la risposta corretta e l’“errore più grave,” utilizziamo una versione morbida di hinge. Questa perdita prova a fare sí che ci sia un “margine infinito”, ma poiché la sua pendenza decade esponenzialmente, questo non accade.

Fig. 5: Perdita Logaritmica

Perdita Square-Square (quadratica-quadratica)

$L_{sq-sq}(W,Y^i,X^i)=E(W,Y^i,X^i)^2+(\max(0,m-E(W,\bar Y^i,X^i)))^2$

Questa perdita comprende l’energia al quadrato e la perdita hinge al quadrato. Questa combinazione tenta di minimizzare l’energia mantenendo un margine di almeno $m$ sulla distanza dall’“errore più grave”. Questo è molto simile alle funzioni di perdita utilizzate nelle reti neurali cosiddette “siamesi” (Siamese nets).

Altre funzioni di perdita

Ne esistono parecchie altre. Qui di seguito riassumiamo le funzioni buone e non.

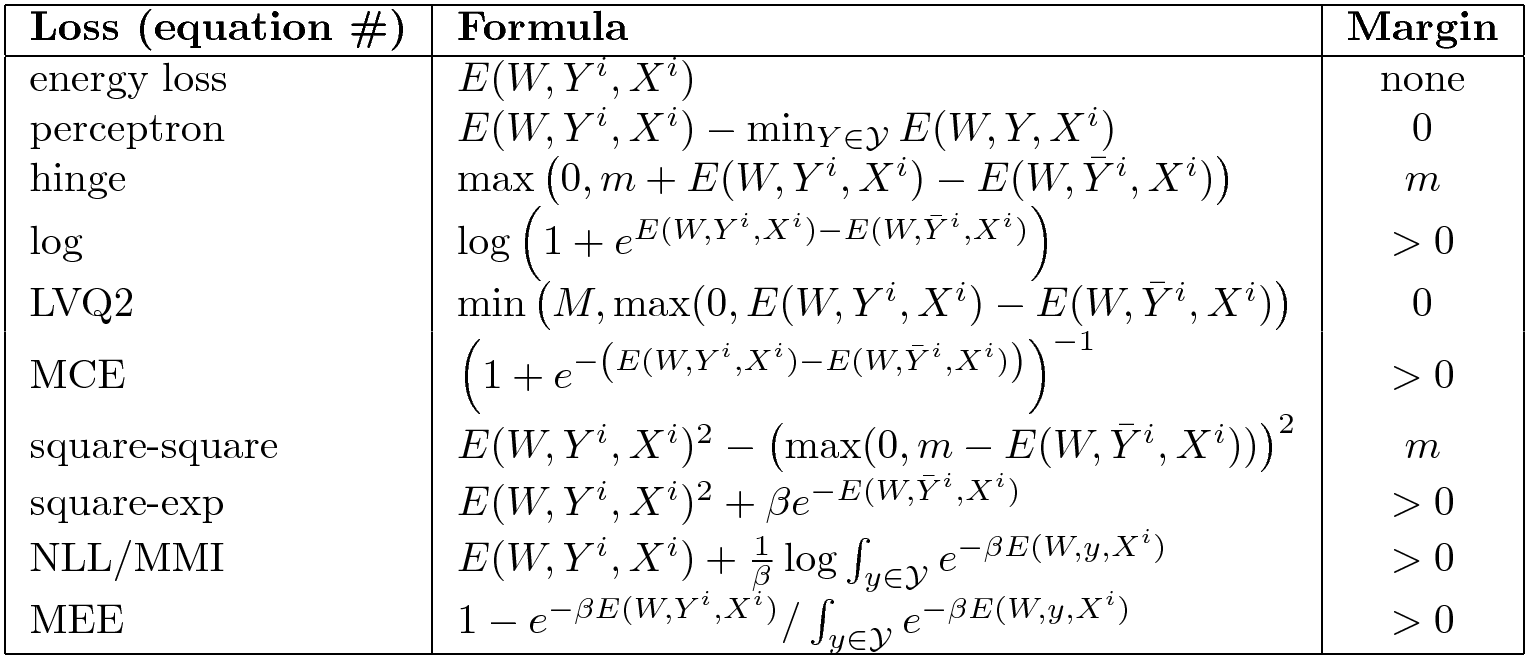
Fig. 6: Selezione delle funzioni di perdita per EBM

La colonna di destra indica se la funzione ad energia impone un margine. La tipica perdita ad energia non spinge alcuna regione verso l’alto e quindi non ha un margine. La perdita ad energia non funziona per ogni tipo di problema. La perdita percettrone non funziona in generale, ma solo quando si ha una parametrizzazione lineare della funzione di energia. Alcune funzioni di perdita hanno un margine finito come la perdita hinge, mentre altre hanno margini infiniti, come la perdita hinge “morbida”.

Domanda: In che modo viene trovato l’“errore più grave” $\bar Y_i$ nel caso continuo?

Risposta: Vogliamo aumentare l’energia dei punti che sono sufficientemente distanti da $Y^i$, perché se ci avviciniamo troppo, i parametri potrebbero non cambiare più di tanto perché la funzione definita da una rete neurale diventa “rigida”. In generale, questo è un problema difficile ed è proprio quello che provano a risolvere i metodi che utilizzano esempi contrastivi. Non c’è un modo giusto per trovarlo.

Una perdita di tipo hinge contrastiva più generica è la seguente:

$L(W,X^i,Y^i)=\sum_y H(E(W, Y^i,X^i)-E(W,y,X^i)+C(Y^i,y))$

Presupponiamo che $Y$ sia discreta (se fosse continua la somma verrebbe sostituita da un integrale). Qui, $E(W, Y^i,X^i)-E(W,y,X^i)$ è la differenza fra $E$ valutato sull’output corretto ed $E$ valutato su un’altro output. $C(Y^i,y)$ è il margine, ed generalmente rappresenta una misura di distanza fra $Y^i$ e $y$. La motivazione per questo è che vogliamo che l’aumentare degli esempi sbagliati $y$ dipenda dalla distanza fra $y$ e l’esempio corretto $Y_i$. Questa può essere una perdita più difficile da ottimizzare.

---

📝 Charles Brillo-Sonnino, Shizhan Gong, Natalie Frank, Yunan Hu
🇮🇹 Francesca Guiso
13 Apr 2020