Funzioni di attivazione e di perdita (parte 1)

🎙️ Yann LeCun

Funzioni di attivazione

In questa lezione, faremo un riassunto delle funzioni di attivazione più importanti e la loro implementazione in PyTorch. Queste provengono da diversi articoli che affermano che ciascuna di esse funzioni meglio per un determinato tipo di problema.

Unità Lineare Rettificata (Rectified Linear Unit, ReLU) - nn.ReLU()

\[\text{ReLU}(x) = (x)^{+} = \max(0,x)\]
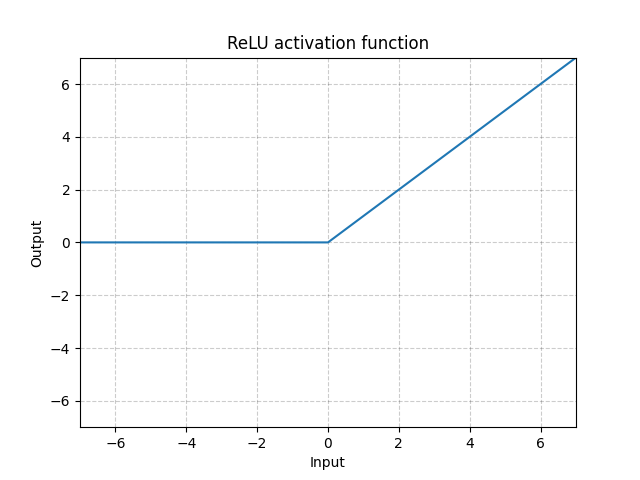
Fig. 1: ReLU

RReLU - nn.RReLU()

Ci sono diverse varianti di ReLU. Definiamo ReLU casuale (Random ReLU, RReLU) come di seguito.

\[\text{RReLU}(x) = \begin{cases} x, & \text{if} x \geq 0\\ ax, & \text{otherwise} \end{cases}\]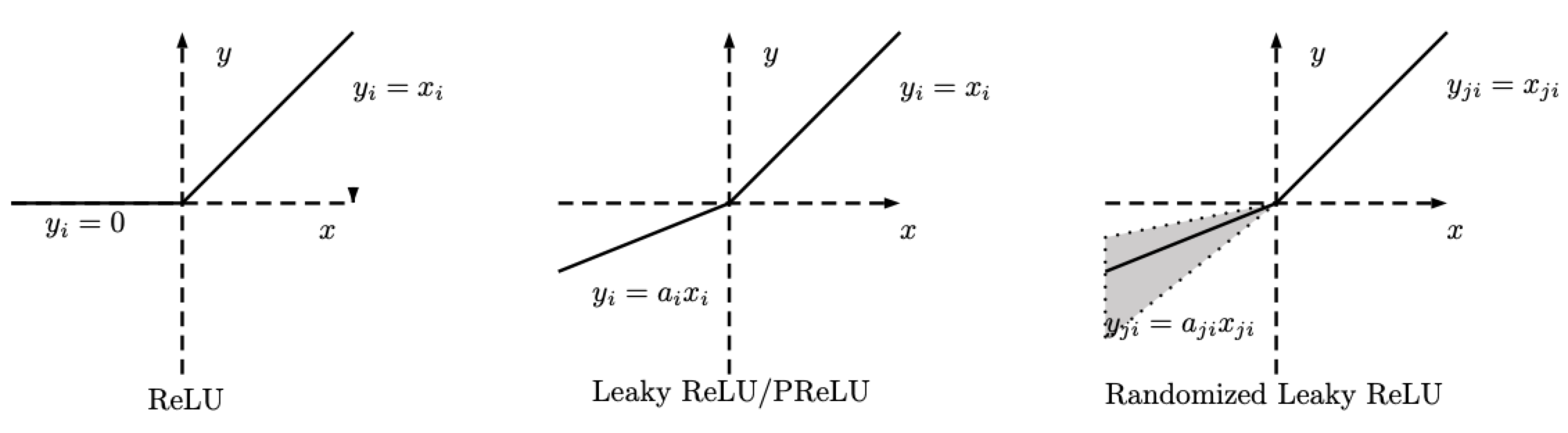
Fig. 2: ReLU, "Leaky" ReLU/PReLU, RReLU

Si noti che per il RReLU, $a$ è una variabile casuale che mantiene i campionamenti in un determinato range durante la fase di addestramento, e che rimane fissa durante la fase di test. Anche nel PReLU , $a$ viene addestrato. Per il Leaky ReLU (ReLU con perdita), $a$ è fisso.

LeakyReLU - nn.LeakyReLU()

\[\text{LeakyReLU}(x) = \begin{cases} x, & \text{if} x \geq 0\\ a_\text{negative slope}x, & \text{otherwise} \end{cases}\]
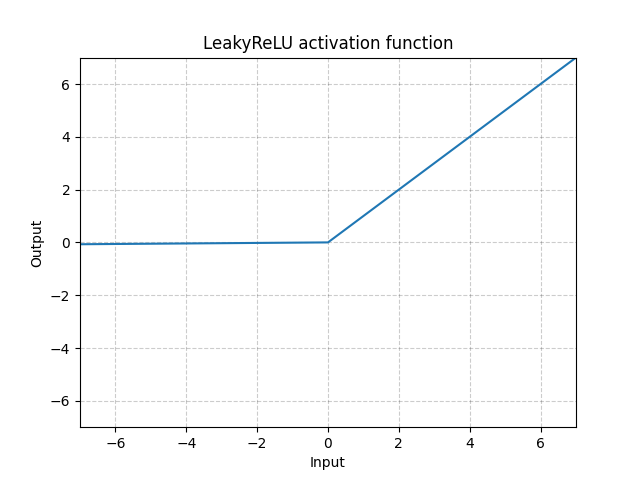
Fig. 3: "Leaky" ReLU

Qui $a$ è un parametro fisso. Il divisore dell’equazione di sopra previene il problema del ReLU “scomparente” (dying ReLU), ovvero che i neuroni ReLU diventino di fatto inattivi, avendo valore 0 per qualunque input, e che anche il gradiente sia 0. Una pendenza negativa permette alla rete di compiere la retro-propagazione e quindi di apprendere .

Il Leaky ReLU è necessario per le reti “fini” (skinny network), in cui è quasi impossibile ottenere gradienti da propagare indietro con il ReLU ordinario. Con il Leaky ReLU la rete può avere un gradiente anche in quelle regioni in cui il ReLU ordinario avrebbe azzerato tutti i valori.

PReLU - nn.PReLU()

\[\text{PReLU}(x) = \begin{cases} x, & \text{if} x \geq 0\\ ax, & \text{otherwise} \end{cases}\]

Qui $a$ è un parametro da addestrare.

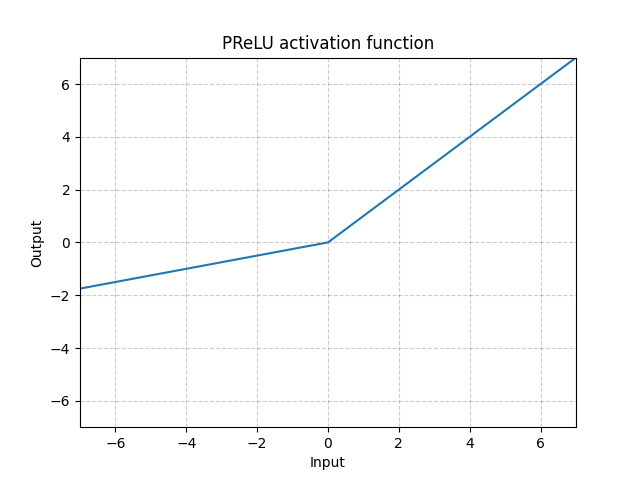
Fig. 4: ReLU

Le funzioni di attivazione di sopra (ReLU, LeakyReLU, PReLU) sono invarianti ai riscalamenti.

Softplus - Softplus()

\[\text{Softplus}(x) = \frac{1}{\beta} * \log(1 + \exp(\beta * x))\]
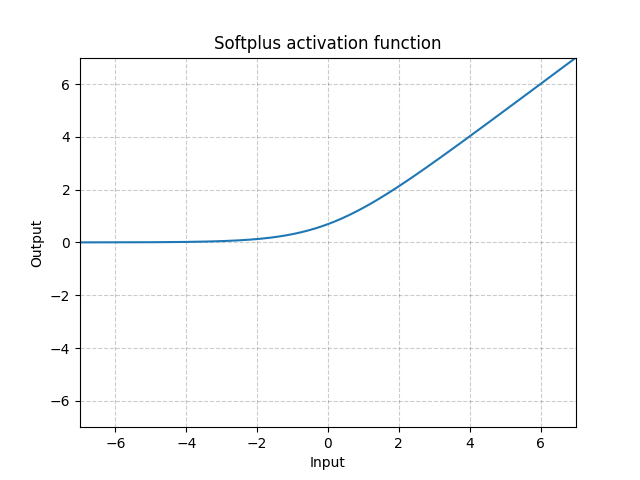
Fig. 5: Softplus

Softplus è un’approssimazione differenziabile (liscia) della funzione ReLU e può essere utilizzata per vincolare l’output in modo che sia sempre positivo. La funzione assomiglia sempre più a ReLU al crescere di $\beta$.

ELU - nn.ELU()

\[\text{ELU}(x) = \max(0, x) + \min(0, \alpha * (\exp(x) - 1)\]
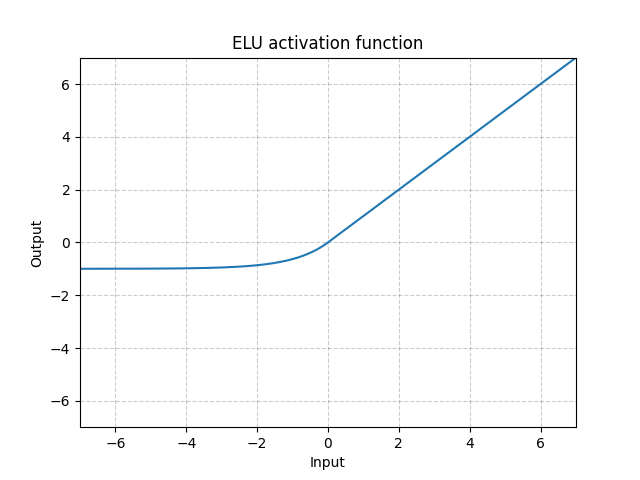
Fig. 6: ELU

Al contrario di ReLU, l’unità lineare esponenziale (Exponential Linear Unit, ELU) può generare valori negativi, permettendo al sistema di avere un output uguale a zero in media. Il modello può quindi convergere più in fretta. Le varianti CELU (Continuously Differentiable Exponential Linear Units) e SELU (Scaled Exponential Linear Unit) sono semplicemente ri-parametrizzazioni di ELU.

CELU - nn.CELU()

\[\text{CELU}(x) = \max(0, x) + \min(0, \alpha * (\exp(x/\alpha) - 1)\]
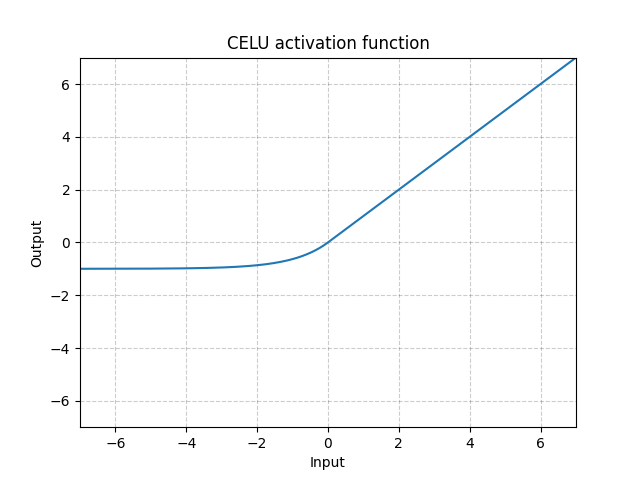
Fig. 7: CELU

SELU - nn.SELU() –>

\[\text{SELU}(x) = \text{scale} * (\max(0, x) + \min(0, \alpha * (\exp(x) - 1))\]
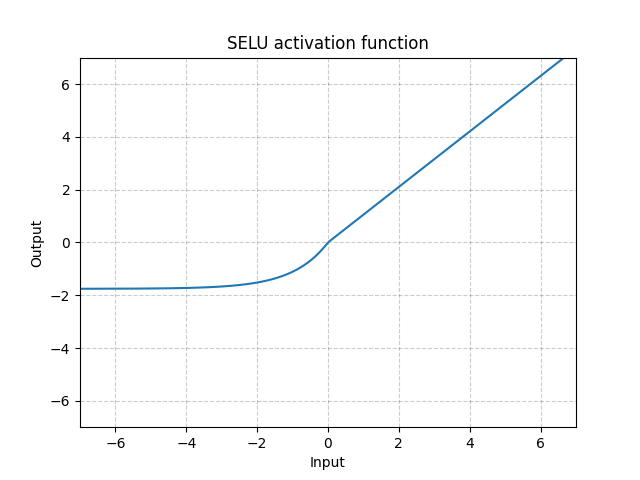
Fig. 8: SELU

GELU - nn.GELU()

\[\text{GELU(x)} = x * \Phi(x)\]

dove $\Phi(x)$ è la funzione di distribuzione cumulativa (cdf) per la distribuzione normale.

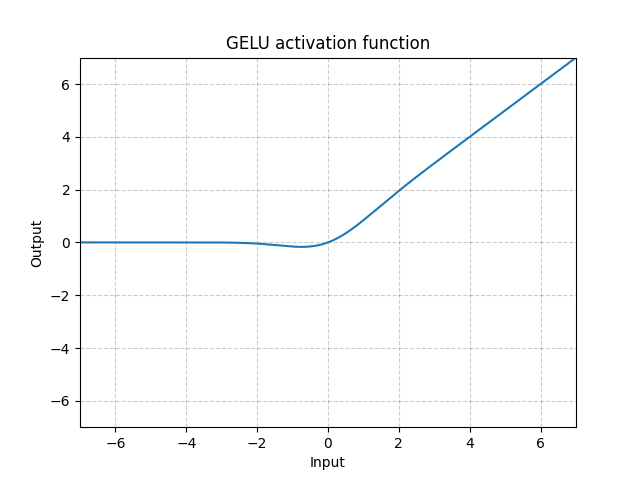
Fig. 9: GELU

ReLU6 - nn.ReLU6()

\[\text{ReLU6}(x) = \min(\max(0,x),6)\]
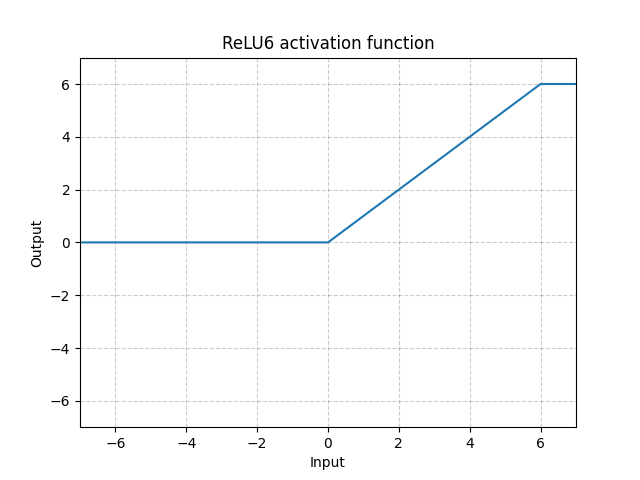
Fig. 10: ReLU6

Questa funzione è la funzione ReLU che si appiattisce a valori pari o maggiori a 6. Tuttavia, non vi è una ragione particolare che motiva la scelta del valore 6. Possiamo invece utilizzare la funzione sigmoide come di seguito.

Sigmoid - nn.Sigmoid()

\[\text{Sigmoid}(x) = \sigma(x) = \frac{1}{1 + \exp(-x)}\]
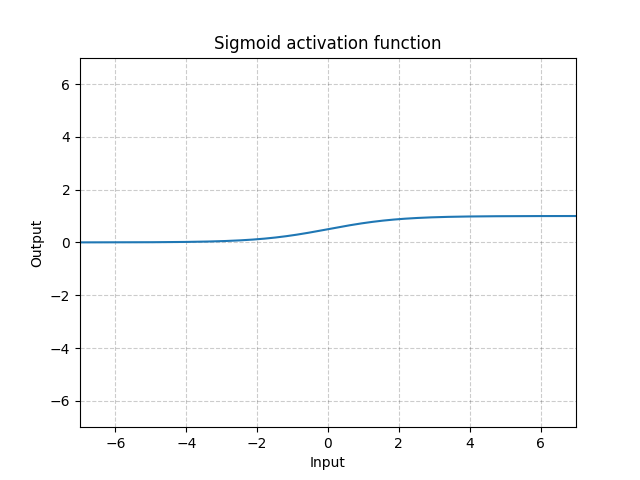
Fig. 11: Funzione Sigmoide

Se accatastiamo funzioni sigmoidi su diversi strati, questo potrebbe creare inefficienza nell’apprendimento della rete e potrebbe dover richiedere un’attenta inizializzazione. Questo perché se l’input è molto grande o molto piccolo, il gradiente della funzione sigmoide è quasi 0. Di consequenza non vi è un gradiente da retro-propagare per aggiornare i parametri della rete, un fenomeno noto come il problema del gradiente saturo (saturated gradient problem). Quindi, per le reti neurali profonde preferiamo una sola funzione di attivazione con un punto angoloso (ad esempio ReLU).

Tanh - nn.Tanh()

\[\text{Tanh}(x) = \tanh(x) = \frac{\exp(x) - \exp(-x)}{\exp(x) + \exp(-x)}\]
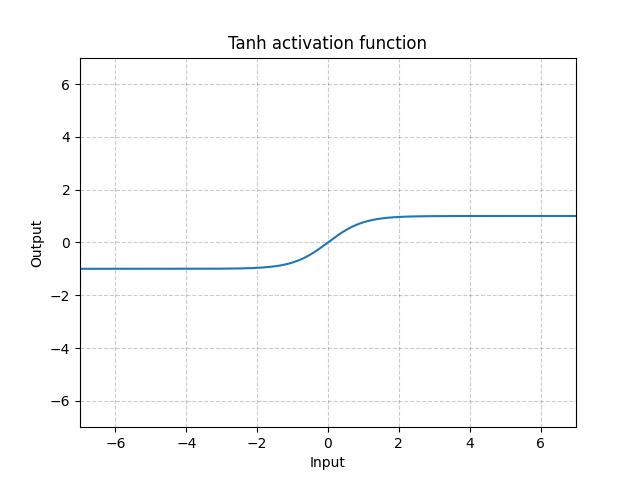
Fig. 12: Tanh

La funzione tangente iperbolica (hyperbolic tangent, tanh) è praticamente identica alla funzione sigmoide tranne per il fatto che è centrata in un intervallo fra -1 e 1. L’output della funzione sarà, di media, vicino allo zero e di consequenza il modello convergerà più velocemente. Si noti che solitamente si converge più velocemente quando ciascun input è di media vicino a zero, come ad esempio la normalizzazione batch (Batch Normalization, BatchNorm).

Softsign - nn.Softsign()

\[\text{SoftSign}(x) = \frac{x}{1 + |x|}\]
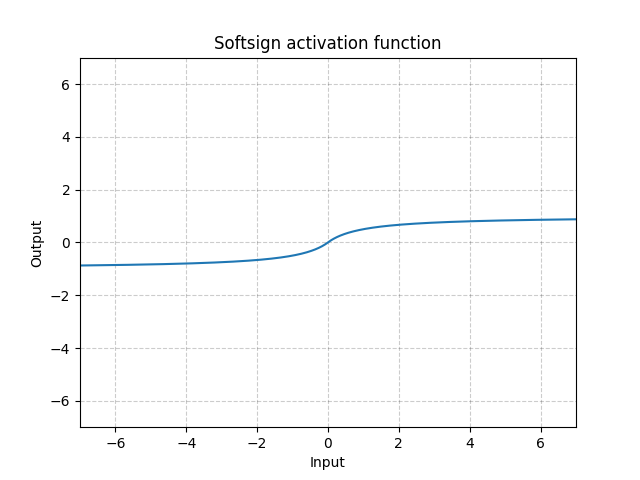
Fig. 13: Softsign

È simile alla funzione sigmoide perché si avvicina all’asintoto lentamente, quindi attenua (fino a un certo punto) il problema del gradiente scomparente (vanishing gradient problem).

Hardtanh - nn.Hardtanh()

\[\text{HardTanh}(x) = \begin{cases} 1, & \text{if} x > 1\\ -1, & \text{if} x < -1\\ x, & \text{otherwise} \end{cases}\]

Il range dell’intervallo lineare [-1, 1] può essere aggiustato utilizzando min_val e max_val.

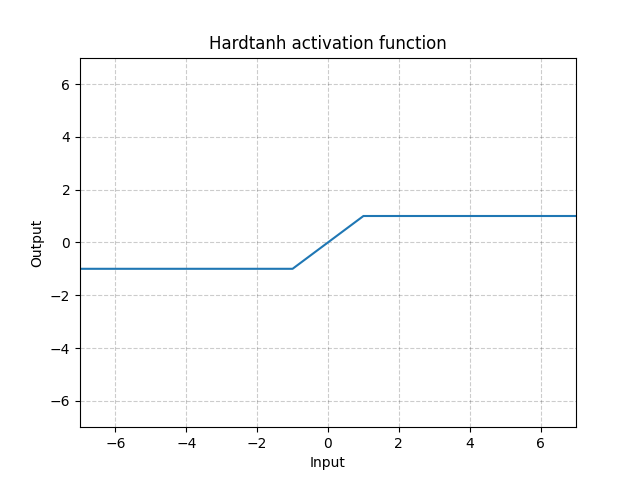
Fig. 14: Hardtanh

Funziona sorprendentemente bene, particolarmente quando si vincolano i pesi in modo che rientrino in un range di valori bassi.

Threshold - nn.Threshold()

\[y = \begin{cases} x, & \text{if} x > \text{threshold}\\ v, & \text{otherwise} \end{cases}\]

Questa funzione viene utilizzata raramente perché non se ne può retro-propagare il gradiente. Anche questo ha impedito che si utilizzasse la retro-propagazione negli anni ‘60 e ‘70, quando si utilizzavano neuroni binari.

Tanhshrink - nn.Tanhshrink()

\[\text{Tanhshrink}(x) = x - \tanh(x)\]
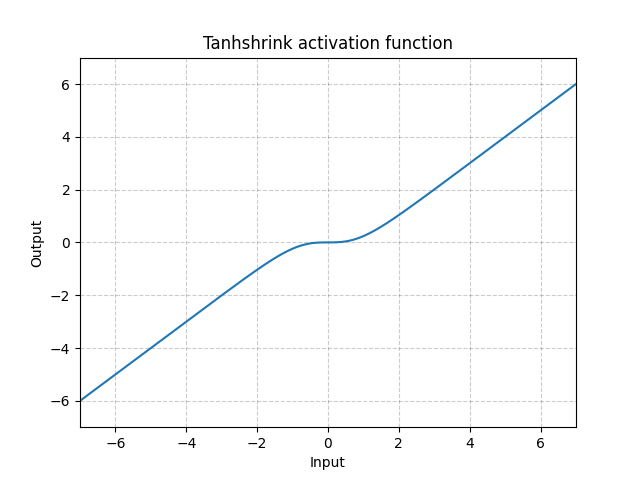
Fig. 15: Tanhshrink

Questa funzione viene utilizzata raramente, se non per calcolare il valore di una variabile latente tramite la codifica rarefatta (sparse coding).

Softshrink - nn.Softshrink()

\[\text{SoftShrinkage}(x) = \begin{cases} x - \lambda, & \text{if} x > \lambda\\ x + \lambda, & \text{if} x < -\lambda\\ 0, & \text{otherwise} \end{cases}\]
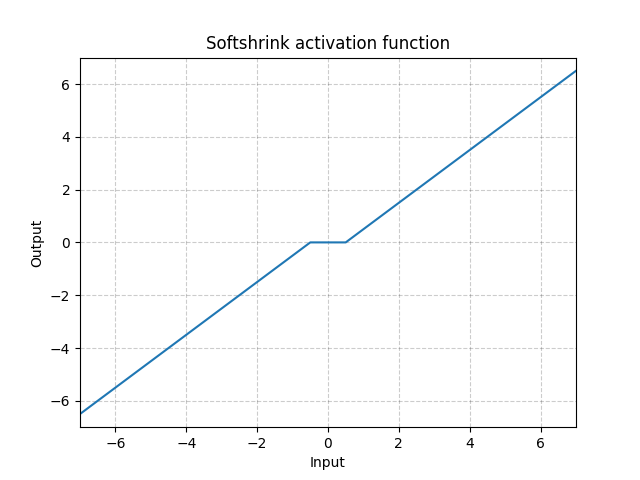
Fig. 16: Softshrink

Questa funzione rimpicciolisce l’input di un fattore costante, e lo manda a zero quando il suo valore si avvicina a zero. La si può pensare come un passo del gradiente secondo il criterio $\ell_1$. La funzione è anche uno dei passi dell’algoritmo Iterative Shrinkage-Thresholding Algorithm (ISTA). Tuttavia, non viene utilizzata frequentemente come attivazione nelle reti neurali standard.

Hardshrink - nn.Hardshrink()

\[\text{HardShrinkage}(x) = \begin{cases} x, & \text{if} x > \lambda\\ x, & \text{if} x < -\lambda\\ 0, & \text{otherwise} \end{cases}\]
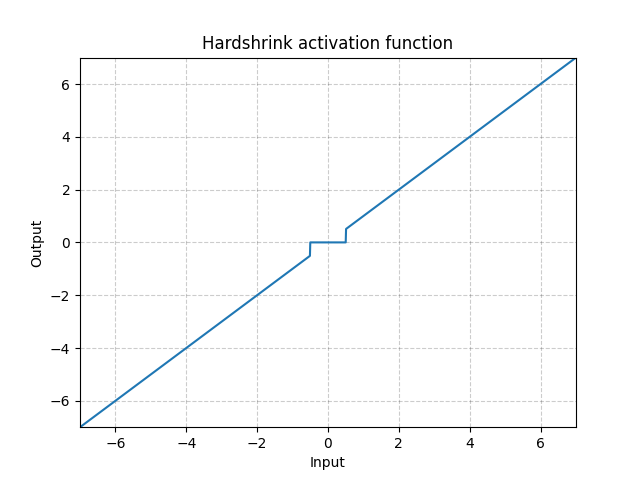
Fig. 17: Hardshrink

Viene utilizzato raramente, se non per la codifica rarefatta.

LogSigmoid - nn.LogSigmoid()

\[\text{LogSigmoid}(x) = \log\left(\frac{1}{1 + \exp(-x)}\right)\]
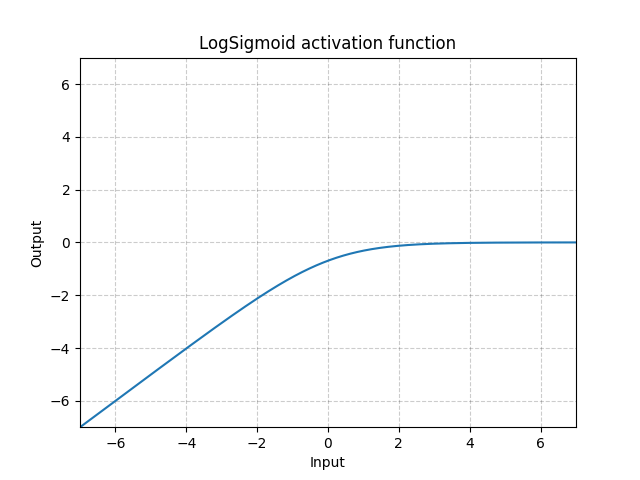
Fig. 18: LogSigmoid

Viene utilizzata principalmente come funzione di perdita, non viene comunemente utilizzata come funzione di attivazione.

Softmin - nn.Softmin()

\[\text{Softmin}(x_i) = \frac{\exp(-x_i)}{\sum_j \exp(-x_j)}\]

Trasforma i numeri in una distribuzione di probabilità.

Soft(arg)max - nn.Softmax()

\[\text{Softmax}(x_i) = \frac{\exp(x_i)}{\sum_j \exp(x_j)}\]

LogSoft(arg)max - nn.LogSoftmax()

\[\text{LogSoftmax}(x_i) = \log\left(\frac{\exp(x_i)}{\sum_j \exp(x_j)}\right)\]

Viene utilizzata principalmente come funzione di perdita, non viene comunemente utilizzata come funzione di attivazione.

Domande e risposte sulle funzioni di attivazione

Domande su nn.PReLU()

• Perché utilizziamo lo stesso valore di $a$ per tutti i canali?

  Si possono avere diversi $a$ per ogni canale. Si può usare $a$ come parametro per ogni unità della rete. Inoltre, $a$ può essere condiviso come mappatura delle caratteristiche.

• $a$ è un valore da apprendere? Ci sono dei vantaggi nell’apprendere $a$?

  $a$ può essere apprendibile oppure fisso. La ragione per cui potremmo voler fissare $a$ è al fine di garantire che l’attivazione non lineare possa avere un gradiente diverso da zero anche nelle regioni negative. Rendere $a$ un parametro apprendibile permette invece al sistema di trasformare la funzione non lineare in una mappatura lineare oppure in un raddrizzamento . Questo potrebbe essere utile per alcune applicazioni, come ad esempio per implementare un rilevatore di edge indipendente dalla sua polarità.

• Quanto dev’essere complessa la funzione non lineare?

  In teoria, possiamo parametrizzare un’intera funzione non lineare in maniera molto complessa, utilizzando ad esempio spring parameters, polinomi di Chebyshev, etc. La parametrizzazione può diventare una parte del processo di apprendimento.

• Qual è un vantaggio della parametrizzazione rispetto ad avere più unità nel sistema?

  Dipende da quello che si vuole fare. Ad esempio, per la regressione in uno spazio a bassa dimensionalità, la paramterizzazione può essere utile. Tuttavia, se il compito è in uno spazio ad alta dimensionalità, come per il riconoscimento delle immagini, può bastare una qualunque funzione non lineare, e le funzioni monotone funzionano meglio. In poche parole, si può parametrizzare qualunque funzione, ma non è detto che questo porti un grande vantaggio.

Domande sui punti angolosi

• Un punto angoloso rispetto a due punti angolosi

  Le funzioni con due punti angolosi creano implicitamente una nozione di scala. Questo significa che se i pesi dell’input vengono moltiplicati per due, o se l’ampiezza del segnale viene moltiplicata per due, gli output saranno completamente diversi. Il segnale potrebbe prendere un valore diverso dalla funzione non lineare, risultando in un comportamento dell’output completamente diverso. Tuttavia, se abbiamo una funzione con un solo punto angoloso, moltiplicare l’input per due risulterebbe semplicemente in un output moltiplicato per due.

• Quali sono le differenze tra le funzioni di attivazione con punti angolosi e quelle non lineari ma lisce? Quando e perché ne preferiamo una rispetto all’altra?

  Si tratta dell’invarianza ai riscalamenti. Se si ha un punto angoloso e moltiplichiamo l’input per due questo risulta in un output moltiplicato per due. Se invece abbiamo una transizione liscia fra una parte della funzione e l’altra, e per esempio moltiplichiamo l’input per 100, l’output potrebbe rassomigliare all’output di una funzione con punto angoloso perché la parte liscia viene rimpicciolita di un fattore di 100. Se si divide l’input per 100, il punto angoloso diventa una funzione convessa molto liscia. Quindi, cambiando la scala dell’input cambiamo il comportamento della funzione di attivazione.

  Talvolta questo può creare problemi. Ad esempio, quando addestriamo una rete neurale con più di uno strato, se abbiamo due strati consecutivi non possiamo controllare la dimensione relativa dei pesi di uno strato e dell’altro. Se abbiamo una funzione non lineare che è “sensibile” alla scala degli input, la rete sarà vincolata dalla dimensione dei pesi da utilizzare nel primo strato, perché cambiarne la dimensione potrebbe risultare in un comportamento completamente diverso.

  Un modo per risolvere questo problema sarebbe di imporre una scala fissa sui pesi di ogni strato cosí da poter normalizzare tutti i pesi a seconda dello strato a cui appartengono, ad esempio con la normalizzazione batch. Di consequenza, la varianza di ciascuna unità della rete diventa fissa. Fissata la scala, il sistema non ha più modo di scegliere quale parte della funzione non lineare da utilizzare se si ha una funzione con due punti angolosi. Questo potrebbe essere un problema se la parte “fissa” dovesse diventare troppo “lineare”. Ad esempio, la funzione sigmoide diventa lineare per valori intorno a zero, e quindi gli output della normalizzazione batch (vicini a zero) potrebbero di fatto non essere attivati da una funzione non lineare.

  Non è del tutto chiaro perché le reti profonde funzionino meglio con funzioni di attivazione con un unico punto angoloso. Probabilmente, questo è dovuto alla loro proprietà di invarianza ai riscalamenti.

Coefficiente di temperatura in una funzione soft(arg)max

• Quando si usa il coefficiente di temperatura e perché viene utilizzato?

  In una certa misura la temperatura è ridondante rispetto ai pesi in ingresso. Se abbiamo delle somme pesate in ingresso alla nostra softmax, il parametro $\beta$ è ridondante rispetto alla dimensione dei pesi.

  La temperatura controlla quanto sarà duro l’output delle distribuzione. Per valori molto grandi di $\beta$ diventa molto vicino all’uno oppure allo zero. Quando $\beta$ è piccolo, è più morbido. Se il limite di $\beta$ è uguale a zero è come una media, se $\beta$ va ad infinito si comporta come argmax e non è più morbido. Quindi, se si ha una forma di normalizzazione prima del softmax, agire su questo parametro permette di controllarne la durezza. A volte si può iniziare con un $\beta$ piccolo in modo da ottenere una discesa del gradiente dal comportamento corretto ed in seguito, mentre l’elaborazione procede e se si vuole una decisione più dura nel meccanismo di soglia, si incrementa $\beta$. Possiamo quindi rifinire le decisioni. Questo trucco viene chiamato tempratura. Per molti esperti è un utile meccanismo di auto attenzione.

Funzioni di perdita

PyTorch ha implementato molte funzioni di perdita. Qui di seguito ne vedremo alcune.

nn.MSELoss()

Questa funzione, anche chiamata perdita L2 (L2 loss) dà l’errore quadratico medio (mean squared error, MSE) - la norma L2 quadrata - fra ogni elemento nell’input $x$ e l’obiettivo $y$.

Se utilizziamo un minibatch di $n$ esempi, ci saranno $n$ perdite, una per ciascun esempio nel batch. Possiamo far sí che la funzione di perdita mantenga queste perdite in un vettore, oppure che li sintetizzi in qualche altro modo.

Se non vogliamo sintetizzare le perdite (specifichiamo reduction='none'), la perdita sarà:

\[l(x,y) = L = \{l_1, \dots, l_N\}^\top, l_n = (x_n - y_n)^2\]

dove $N$ è la dimensione del batch, $x$ e $y$ sono i tensor di dimensione arbitraria con un totale di $n$ elementi ciascuno.

Le alternative per sintetizzare sono come di seguito (si noti che il valore predefinito è la media, ovvero reduction='mean').

\[l(x,y) = \begin{cases}\text{mean}(L), \quad &\text{if reduction='mean'}\\ \text{sum}(L), \quad &\text{if reduction='sum'} \end{cases}\]

L’operazione di somma opera comunque su ciascun elemento, che poi viene diviso per $n$.

Si può evitare la divisione per $n$ selezionando reduction = 'sum'.

nn.L1Loss()

Questo misura l’errore assoluto medio (mean absolute error, MAE) fra ciascun elemento dell’input $x$ e dell’obiettivo $y$ (o fra l’output reale e l’output atteso).

Se non sintetizziamo (specifichiamo reduction='none'), la perdita sarà:

\[l(x,y) = L = \{l_1, \dots, l_N\}^\top, l_n = \vert x_n - y_n\vert\]

dove $N$ è la dimensione del batch, $x$ e $y$ sono i tensor di dimensione arbitraria con un totale di $n$ elementi ciascuno.

Vi sono alternative di sintesi (reduction), come prendere la media ('mean') o la somma ('sum'), che funzionano come le reduction di nn.MSELoss().

Modi d’uso: La perdita L1 (L1 loss) è più robusta rispetto a valori anomali e rumore rispetto alla perdita L2. Con la perdita L2, si prende il quadrato dell’errore sui valori anomali/rumorosi, quindi la funzione di costo è molto sensibile a tali valori.

Problema: La perdita L1 non è differenziabile al minimo (0). Quindi dobbiamo prestare attenzione quando ne prendiamo il gradiente (ovvero, con Softshrink). Questo problema motiva la perdita L1 “liscia” (SmoothL1Loss) come di seguito.

nn.SmoothL1Loss()

Questa funzione utilizza la perdita L2 se l’errore assoluto per elemento è minore di 1, la perdita L1 altrimenti.

\[\text{loss}(x, y) = \frac{1}{n} \sum_i z_i\]

dove $z_i$ è dato da

\[z_i = \begin{cases}0.5(x_i-y_i)^2, \quad &\text{if } |x_i - y_i| < 1\\ |x_i - y_i| - 0.5, \quad &\text{otherwise} \end{cases}\]

Anch’essa ha diversi metodi di sintesi (reduction).

Questa funzione è stata pubblicizzata da Ross Girshick (Fast R-CNN). La funzione di perdita L1 liscia (Smooth L1 Loss) è anche nota come perdita di Huber (Huber Loss), oppure come rete “elastica” (Elastic Network) quando la si utilizza come funzione obiettivo.

Modi d’uso: È meno sensibile ai valori estremi rispetto alla perdita dell’errore quadratico medio (MSELoss) ed è liscia per i valori bassi. Questa funzione viene usata spesso per la (computer vision, CV) per resistere ai valori estremi.

Problema: Questa funzione ha una scala ($0.5$ nella funzione di sopra).

L1 vs. L2 for Computer Vision

Nella fase di previsione, abbiamo diversi $y$:

• Se utilizziamo MSE (perdita L2), la previsione sarà una media di tutte le possibili $y$, che nella CV costituisce un’immagine sfocata.
• Se utilizziamo la perdita L1, il valore di $y$ che minimizza la norma L1 è la mediana, ovvero uno dei valori di $y$ e quindi non è sfocato. Si noti però che la mediana è difficile da definire in spazi pluri-dimensionali.

L’utilizzo di L1 porta ad una immagine più nitida per la previsione.

nn.NLLLoss()

È la funzione di perdita negative log-likelihood che si utilizza per addestrare un classificatore con C classi.

Si noti che, matematicamente, l’input della NLLLoss dovrebbe essere composto da verosomiglianze logaritmiche, ma PyTorch non impone questo vincolo. Questo ha l’effetto di rendere il componente desiderato grande a piacere.

La versione “non ridotta” (ovvero, con :attr:reduction settato su 'none') della perdita è come di seguito:

\[\ell(x, y) = L = \{l_1,\dots,l_N\}^\top, \quad l_n = - w_{y_n} x_{n,y_n}, \quad w_{c} = \text{weight}[c] \cdot \mathbb{1}\{c \not= \text{ignore\_index}\}\]

dove $N$ è la dimensione del batch.

Se la reduction non è 'none' (il valore predefinito è 'mean'), allora la perdita è come di seguito:

\[\ell(x, y) = \begin{cases} \sum_{n=1}^N \frac{1}{\sum_{n=1}^N w_{y_n}} l_n, & \text{if reduction} = \text{'mean';}\\ \sum_{n=1}^N l_n, & \text{if reduction} = \text{'sum'.} \end{cases}\]

Questa funzione di perdita ha un argomento facoltativo, weight (peso), un tensore 1D, con il quale si assegna un peso a ciascuna delle classi. Questo è utile quando si ha un dataset di addestramento sbilanciato.

Pesi & classi sbilanciate:

Il vettore di pesi è utile se la frequenza delle categorie/classi è diversa. Ad esempio, la frequenza dell’influenza è maggiore della frequenza del tumore ai polmoni. Possiamo semplicemente aumentare il peso per quelle categorie che hanno frequenza minore.

Tuttavia, invece di settare il peso, è meglio pareggiare la frequenza degli esempi durante la fase di addestramento in modo da poter sfruttare al meglio la discesa stocastica del gradiente.

Per pareggiare la frequenza delle classi durante la fase di addestramento, mettiamo gli esempi di ciascuna classe in diversi “bidoni”. Poi generiamo ciascuna minibatch estraendo lo stesso numero di esempi da ciascun bidone. Una volta esauriti gli esempi da estrarre dal bidone più piccolo, procediamo reiterando sugli esempi del bidone più piccolo finché non esauriamo gli esempi della classe prevalente. Questo metodo ci offre la stessa frequenza per tutte le categorie iterando attraverso questi bidoni. Si noti che non si dovrebbe mai pareggiare le classi senza utilizzare tutti gli esempi della categoria più prevalente – non si lasciano indietro dati!

Una problematica evidente del metodo di sopra è che la nostra rete non rileverebbe la frequenza relativa di ciascuna categoria. Per risolvere questo problema, ritocchiamo il sistema addestrando alla fine un paio di epoche sui dati che riflettono la vera frequnza delle categorie, così che il sistema si adatti agli errori sistematici dello strato di output, favorendo le categorie che si verificano più frequentemente.

Per sviluppare un po’ di intuizione per questo schema, ritorniamo all’esempio dal campo medico. Gli studenti di medicina studiano le malattie rare tanto quanto le malattie frequenti (anzi, forse studiano di più le malattie rare, che spesso sono anche le più complesse). Imparano ad adattarsi alle caratteristiche di ognuna di esse, correggendo poi per distinguere quelle rare.

nn.CrossEntropyLoss()

Questa funzione combina nn.LogSoftmax e nn.NLLLoss in una singola classe. L’unione delle due funzioni rende il punteggio della classe corretta il più grande possibile.

La ragione per cui le due funzioni vengono messe insieme è per garantire la stabilità numerica del calcolo del gradiente. Quando il valore del softmax è vicino a $1$ o $0$, il suo logaritmo può avvicinarsi a $0$ o $-\infty$. La pendenza del logaritmo intorno a $0$ ê vicino a $\infty$, il che crea problemi numerici nel passo intermedio della retropropagazione. Combinando le due funzioni i gradienti si saturano fornendoci, alla fine, un risultato accettabile.

L’input dovrebbe essere il punteggio non normalizzato per ciascuna classe.

La perdita può esser descritta con:

\[\text{loss}(x, c) = -\log\left(\frac{\exp(x[c])}{\sum_j \exp(x[j])}\right) = -x[c] + \log\left(\sum_j \exp(x[j])\right)\]

o nel caso in cui viene specificato l’argomento weight:

\[\text{loss}(x, c) = w[c] \left(-x[c] + \log\left(\sum_j\exp(x[j])\right)\right)\]

Prendiamo la media delle perdite sulle osservazioni di ciascun minibatch.

La perdita Cross Entropy ha un’interpretazione nella fisica, legata alla Kullback–Leibler divergence (KL divergence), con la quale si misura la divergenza fra due distribuzioni. Qui, le pseudo-distribuzioni vengono rappresentate dal vettore $x$ (le previsioni) e la distribuzione di target (un vettore one-hot che ha valore 0 per le classi sbagliate e 1 per le classi corrette).

Matematicamente, abbiamo:

\[H(p,q) = H(p) + \mathcal{D}_{KL} (p \mid\mid q)\]

dove \(H(p,q) = - \sum_i p(x_i) \log (q(x_i))\) è la cross-entropy (fra le due distribuzioni), \(H(p) = - \sum_i p(x_i) \log (p(x_i))\) è la entropy, e \(\mathcal{D}_{KL} (p \mid\mid q) = \sum_i p(x_i) \log \frac{p(x_i)}{q(x_i)}\) è la KL divergence.

nn.AdaptiveLogSoftmaxWithLoss()

Questa è un’approssimazione efficiente della funzione di softmax per un grande numero di classi (ad esempio, milioni di classi). Questa funzione sfrutta dei trucchi per aumentare la velocità di computazione.

I dettagli di questo metodo vengono descritti in Efficient softmax approximation for GPUs di Edouard Grave, Armand Joulin, Moustapha Cissé, David Grangier, Hervé Jégou.

---

📝 Haochen Wang, Eunkyung An, Ying Jin, Ningyuan Huang
Francesca Guiso
13 Apr 2020