Il controllore per la retromarcia di un camion

Configurazione del problema

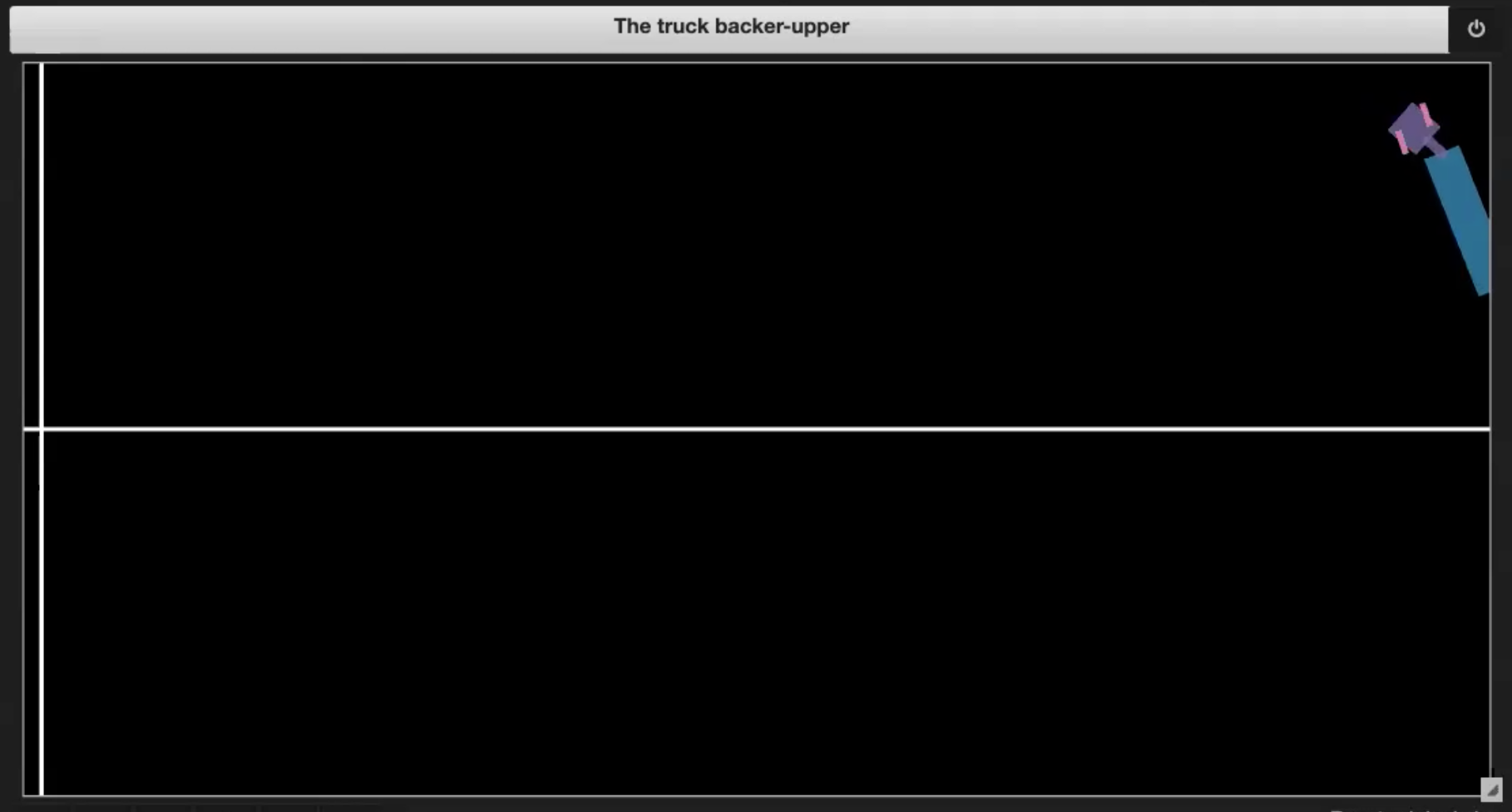
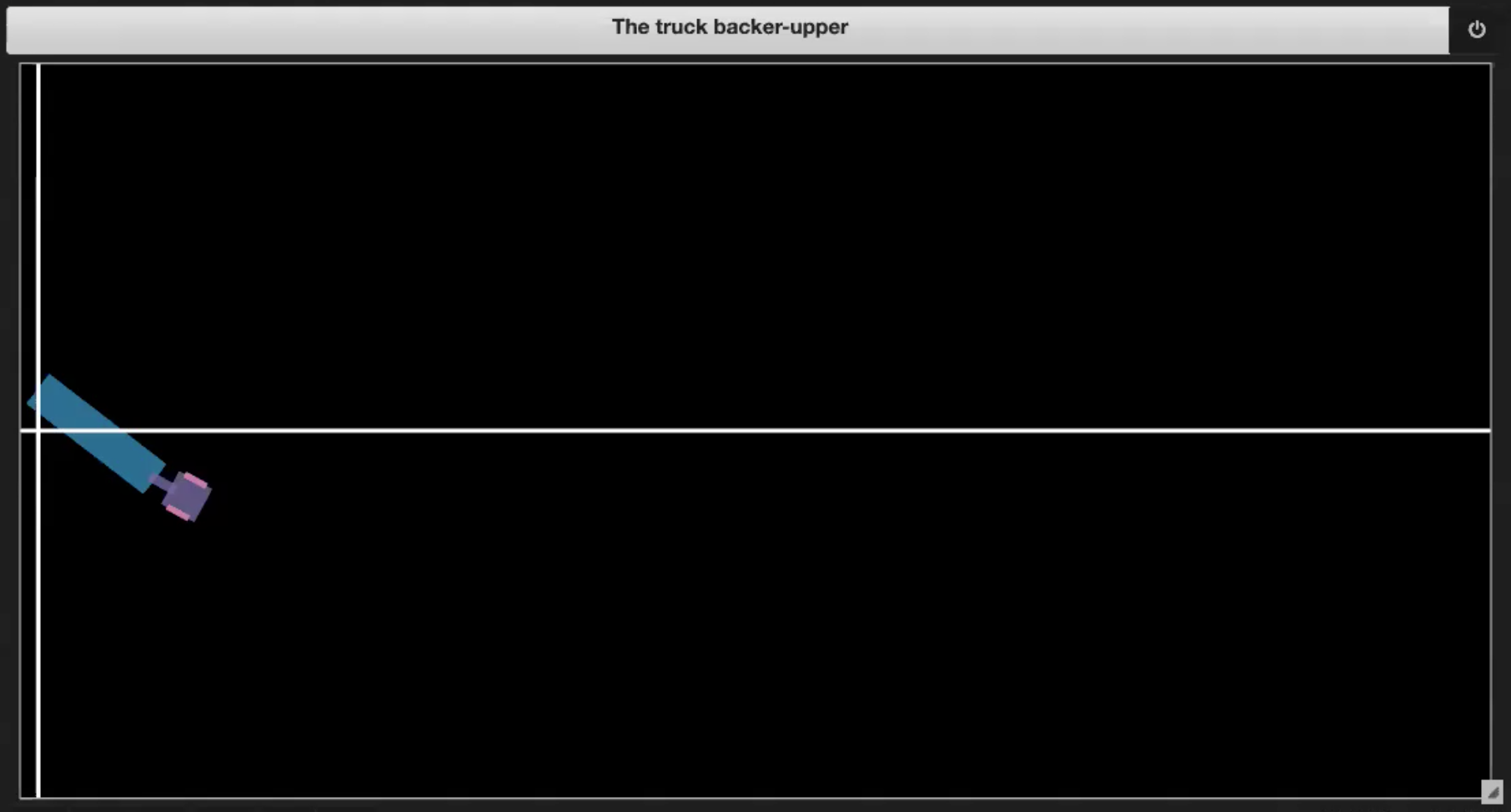
L’obiettivo di questo compito è la costruzione di un controllore auto-supervisionato (self-supervised controller) che controlli lo sterzo di un camion mentre percorre in retromarcia il percorso da una posizione iniziale arbitraria ad una piattaforma di carico.

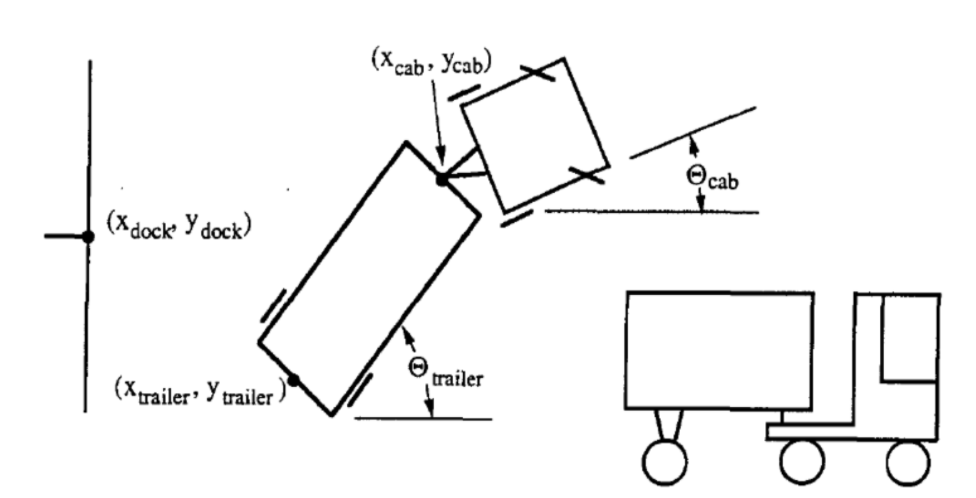
Si noti che è permesso solamente muoversi in retromarcia, come mostrato nella Fig. 1.

|| |

Lo stato del camion è rappresentato da sei parametri:

• $\tcab$: l’angolo del camion (rispetto all’orizzontale)
• $\xcab, \ycab$ le coordinate cartesiane della ralla (o della testa del rimorchio)
• $\ttrailer$: l’angolo del rimorchio
• $\xtrailer, \ytrailer$: le coordinate cartesiane del (retro del) rimorchio

<!– - $\tcab$: Angle of the truck

• $\xcab, \ycab$: The cartesian of the yoke (or front of the trailer).
• $\ttrailer$: Angle of the trailer
• $\xtrailer, \ytrailer$: The cartesian of the (back of the) trailer. –>

L’obiettivo del controllore è selezionare un angolo appropriato $\phi$ per ogni intervallo di tempo $k$, alla fine del quale il camion effettuerà la retromarcia percorrendo una piccola distanza fissa. Il successo prescinde da due criteri:

1. Il retro del rimorchio è parallelo al muro della piattaforma di carico, ovvero $\ttrailer = 0$, e
2. Il retro del rimorchio $\xtrailer, \ytrailer$ è più vicino possibile alle coordinate puntuali della piattaforma ($x_{dock}, y_{dock}$) come mostrato nella figura sopra.

Parametri e visualizzazioni aggiuntive

|| |

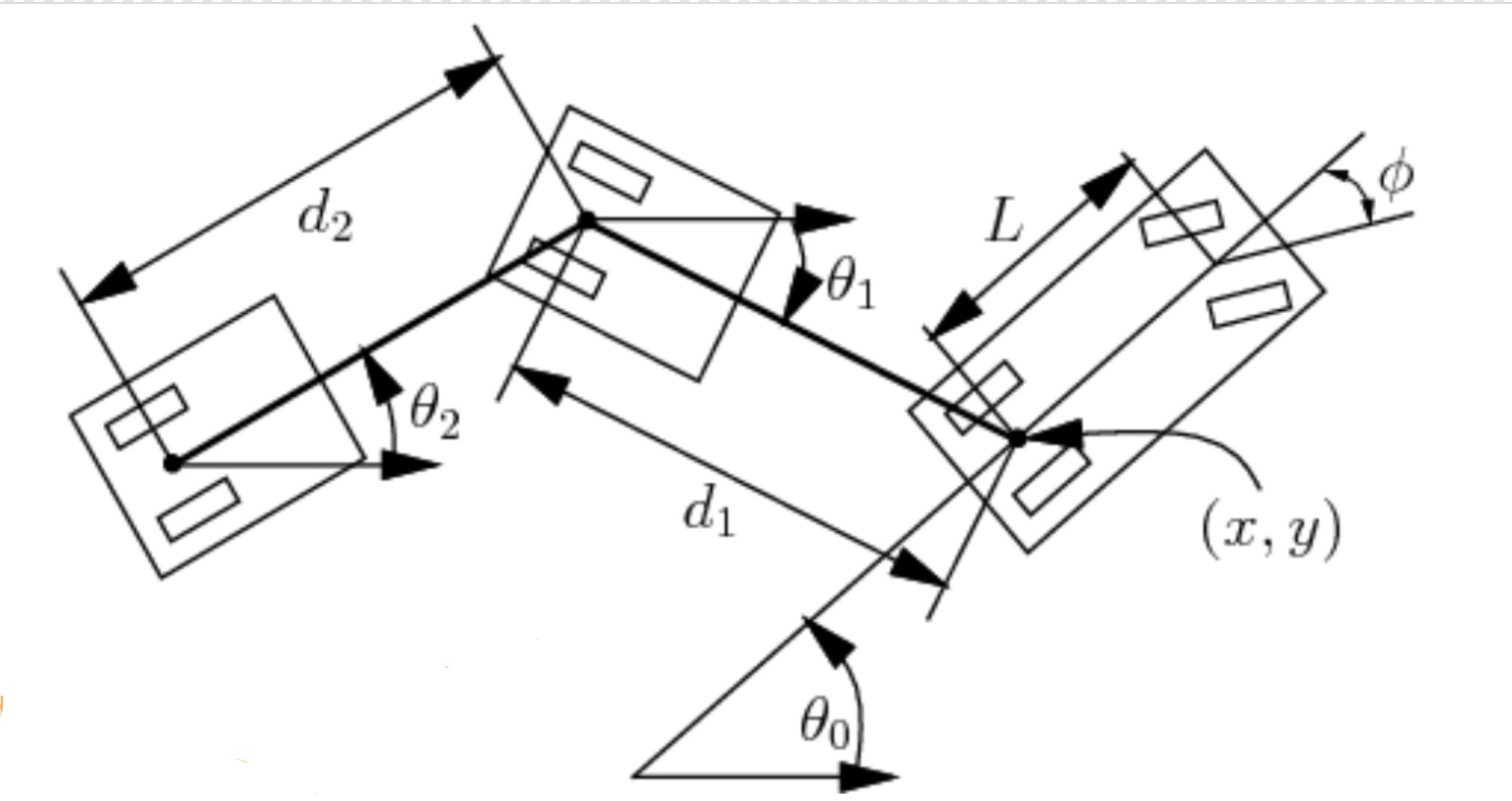
In questa sezione, consideriamo un gruppo di parametri aggiuntivi come mostrato nella Fig. 2. Data la lunghezza $L$ della cabina di guida, $d_1$ è la distanza fra cabina e rimorchio e $d_2$ la distanza del rimorchio. Possiamo ora calcolare la variazione di angolo e posizione:

dove $s$ denota la velocità (di segno positivo e negativo) e $\phi$ l’angolo negativo di sterzata. Ora possiamo rappresentare lo stato solamente tramite quattro parametri: $\xcab$, $\ycab$, $\theta_0$ e $\theta_1$. Ciò perché i parametri di lunghezza $\xtrailer, \ytrailer$ sono noti in quanto ricavabili da $\xcab, \ycab, d_1, \theta_1$.

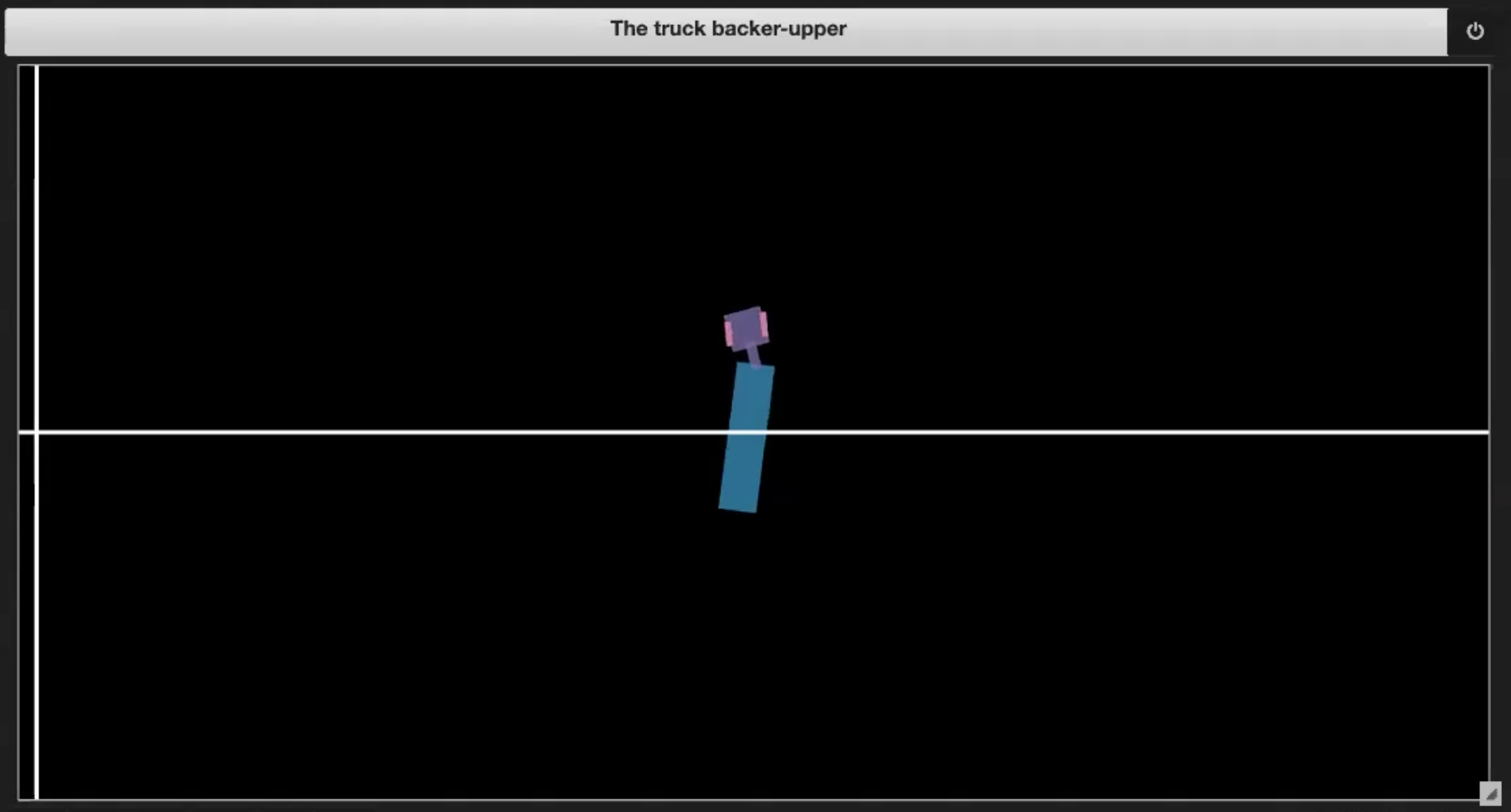
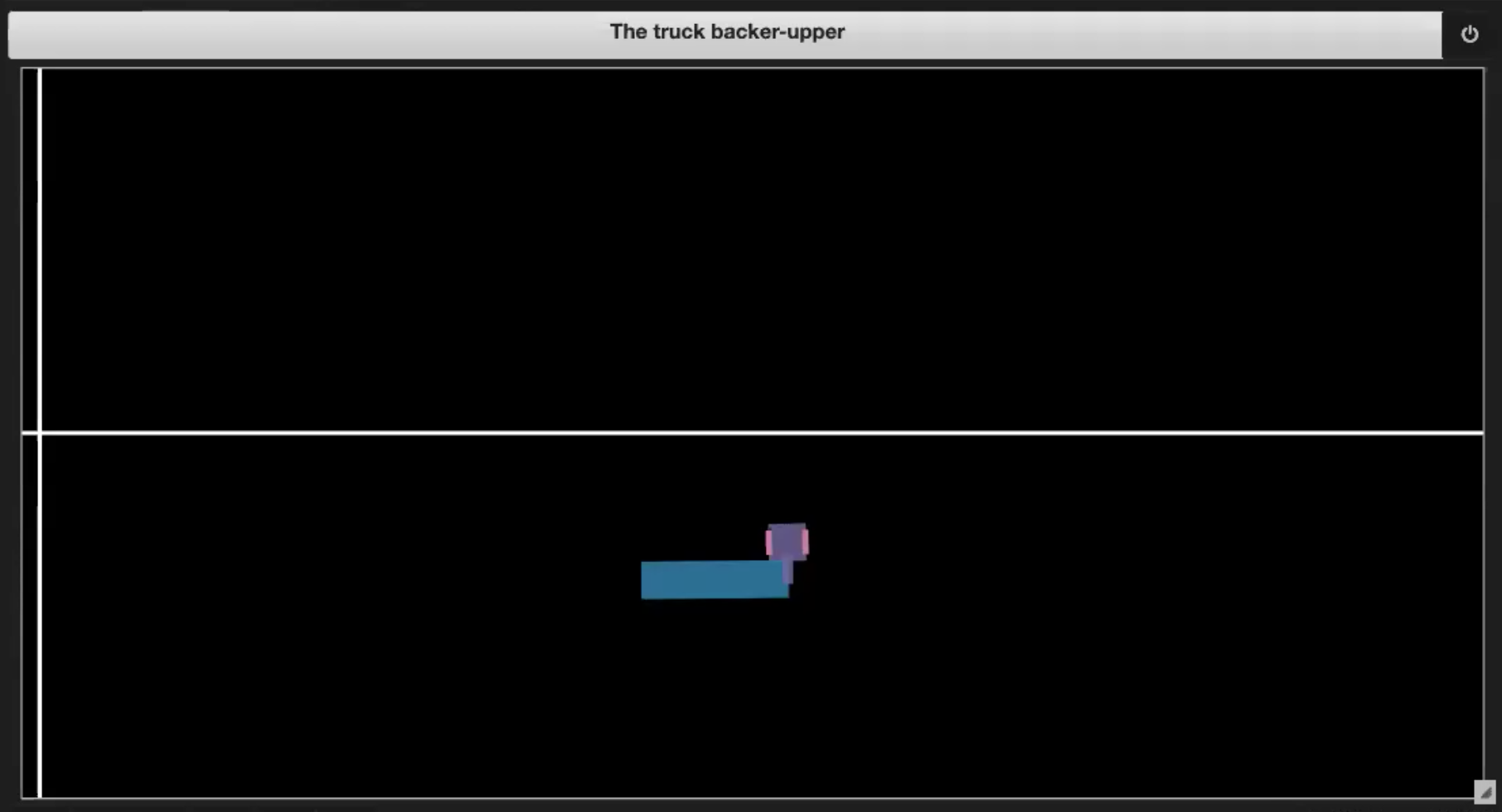
Nel Jupyter Notebook della repository Deep Learning, troviamo degli ambienti di esempio, come mostrato nelle Figg. 3.1-3.4:

Fig. 3.1: grafico di esempio dell’ambiente	Fig. 3.2: chiusura a libro della cabina sul rimorchio (effetto jackknife)
Fig. 3.3: uscita dai bordi	Fig. 3.4: raggiungimento della piattaforma

Ad ogni intervallo temporale $k$ viene inviato un segnale di sterzo compreso fra $-\frac{\pi}{4}$ e $\frac{\pi}{4}$ e il camion si muoverà in retro dell’angolo corrispondente.

Ci sono numerose situazioni in cui la simulazione può essere interrotta:

• il camion si accartoccia su se stesso (chiusura a libro della cabina sul rimorchio, anche conosciuto come “effetto jackknife”, v. Fig. 3.2);
• il camion esce dai bordi dell’ambiente di simulazione (v. Fig. 3.3);
• il camion raggiunge la piattaforma di carico (v. Fig. 3.4).

Addestramento

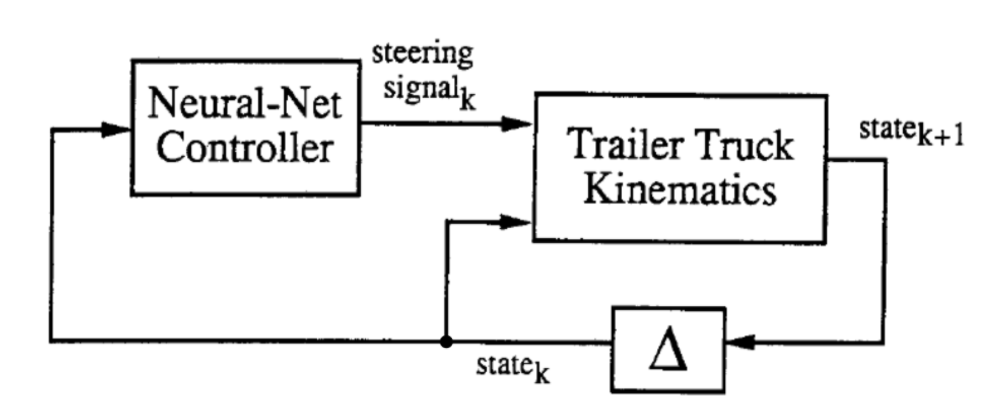
Il processo di addestramento si costituisce di due momenti: (1) addestramento di una rete neurale ad emulazione delle cinematiche concernenti il camion e il rimorchio e (2) addestramento di una rete neurale come controllore del camion.

| | |

Come mostrato qui sopra, nel diagramma astratto, i due blocchi sono le due reti che vanno addestrate. Ad ogni intervallo temporale $k$, la rete chiamata Trailer Truck Kinematics (“cinematiche del rimorchio e del camion”), che chiamiamo “emulatore” (emulator), riceve in input il vettore di stato esadimensionale e il segnale di sterzata generato dal controllore (Neural-Net Controller) e genera un nuovo stato esadimensionale per l’intervallo $k+1$.

L’emulatore

L’emulatore prende in input la posizione corrente ($\tcab^t$,$\xcab^t, \ycab^t$, $\ttrailer^t$, $\xtrailer^t$, $\ytrailer^t$) e la direzione di sterzo ($\phi^t) e restituisce lo stato all’intervallo temporale successivo ($\tcab^{t+1}$,$\xcab^{t+1}, \ycab^{t+1}$, $\ttrailer^{t+1}$, $\xtrailer^{t+1}$, $\ytrailer^{t+1}$). È una rete neurale con uno strato nascosto densamente connnesso e funzione di attivazione ReLU, più uno strato di output lineare. Si utilizza l’errore quadratico medio (MSE, Mean Square Error) come funzione di perdita e si addestra l’emulatore tramite la discesa stocastica del gradiente.

Fig. 5: Addestramento della rete neurale-emulatore

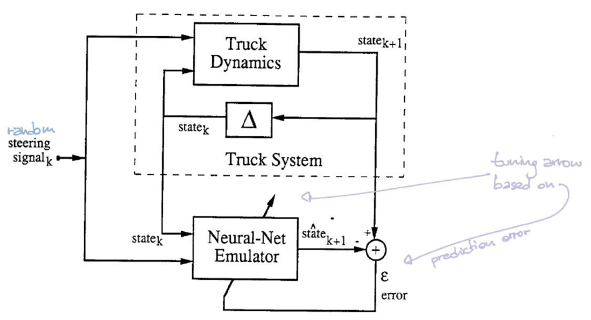Data questa configurazione, il simulatore ci fornisce la posizione del prossimo intervallo data la posizione attuale e l’angolo di sterzo. Di conseguenza, non abbiamo veramente bisogno di una rete neurale che emuli il simulatore. Tuttavia, in sistemi più complessi, potremmo non avere accesso alle equazioni sottostanti il sistema, ovvero alle leggi universali poste in una forma che agevola la computazione. Potremmo ipoteticamente osservare solamente i dati di sequenze di segnali di sterzo e i corrispondenti percorsi del camion. In questo caso, si vuole addestrare una rete per emulare le dinamiche di questo sistema complesso.

Per addestrare l’emulatore, ci sono due funzioni importanti nel file Class truck che necessitano di essere analizzate quando addestriamo l’emulatore.

La prima delle due è la funzione step, che definisce lo stato di output del camion al termine della computazione.

def step(self, ϕ=0, dt=1):

    # controllo di condizioni illegali
    if self.is_jackknifed(): # Jackknife
        print('The truck is jackknifed!')
        return

    if self.is_offscreen(): # Camion fuori schermo
        print('The car or trailer is off screen')
        return

    self.ϕ = ϕ
    x, y, W, L, d, s, θ0, θ1, ϕ = self._get_atributes()

    # aggiornamento dello stato
    self.x += s * cos(θ0) * dt
    self.y += s * sin(θ0) * dt
    self.θ0 += s / L * tan(ϕ) * dt
    self.θ1 += s / d * sin(θ0 - θ1) * dt

La seconda è la funzione stato che restituisce lo stato corrente del camion.

def state(self):
        return (self.x, self.y, self.θ0, *self._traler_xy(), self.θ1)

Prima di tutto vengono generate due liste. Generiamo una lista di input aggiungendo l’angolo di sterzo ϕ e lo stato iniziale del camion tramite la chiamata truck.state(); dopodiché generiamo una lista di output concatenando le variabili di output che possono venir calcolate chiamando truck.step(ϕ).

Ora si può addestrare l’emulatore:

cnt = 0
for i in torch.randperm(len(train_inputs)):
    ϕ_state = train_inputs[i]
    next_state_prediction = emulator(ϕ_state)

    next_state = train_outputs[i]
    loss = criterion(next_state_prediction, next_state)

    optimiser_e.zero_grad()
    loss.backward()
    optimiser_e.step()

    if cnt == 0 or (cnt + 1) % 1000 == 0:
        print(f'{cnt + 1:4d} / {len(train_inputs)}, {loss.item():.10f}')
    cnt += 1

Si noti che la chiamata torch.randperm(len(train_inputs)) restituisce una permutazione casuale degli indici da $0$ alla lunghezza degli input di addestramento meno $1$. Dopo la permutazione degli indici, ad ogni intervallo viene selezionato ϕ_state dalla i-esima posizione della lista di input. Si passa ϕ_state alla funzione di emulazione, la quale produce uno strato di output lineare, e otteniamo la previsione per il prossimo stato (next_state_prediction). L’emulatore è una rete neurale definita qui sotto:

emulator = nn.Sequential(
    nn.Linear(steering_size + state_size, hidden_units_e),
    nn.ReLU(),
    nn.Linear(hidden_units_e, state_size)
)

Si utilizza MSE per calcolare la perdita fra la lo stato reale e quello previsto: lo stato reale proviene dall’i-esimo elemento della lista di output, corrispondente al ϕ_state ottenuto dalla lista di input.

Il controllore

Con riferimento alla Fig. 5, il blocco $\matr{C}$ rappresenta il controllore. Riceve in ingresso lo stato corrente e restituisce un angolo di sterzo. Il blocco $\matr{T}$ (l’emulatore) riceve sia lo stato che l’angolo e produce lo stato successivo.

Fig. 5: diagramma di flusso per la transizione dello stato

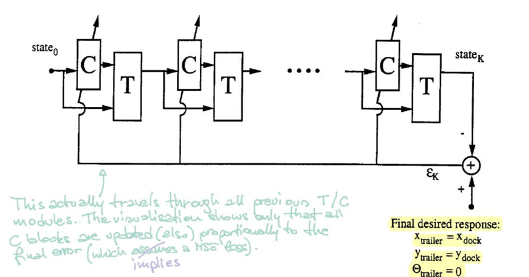Per l’addestramento del controllore, iniziamo da uno stato iniziale casuale e ripetiamo la procedura ($\matr{C}$ e $\matr{T}$) finché il rimorchio si trova parallelo alla piattaforma. L’errore è calcolato comparando la posizione del rimorchio e quella della piattaforma. Ricaviamo quindi i gradienti usando la retropropagazione e aggiorniamo i parametri del controllore tramite SGD.

Struttura dettagliata del modello

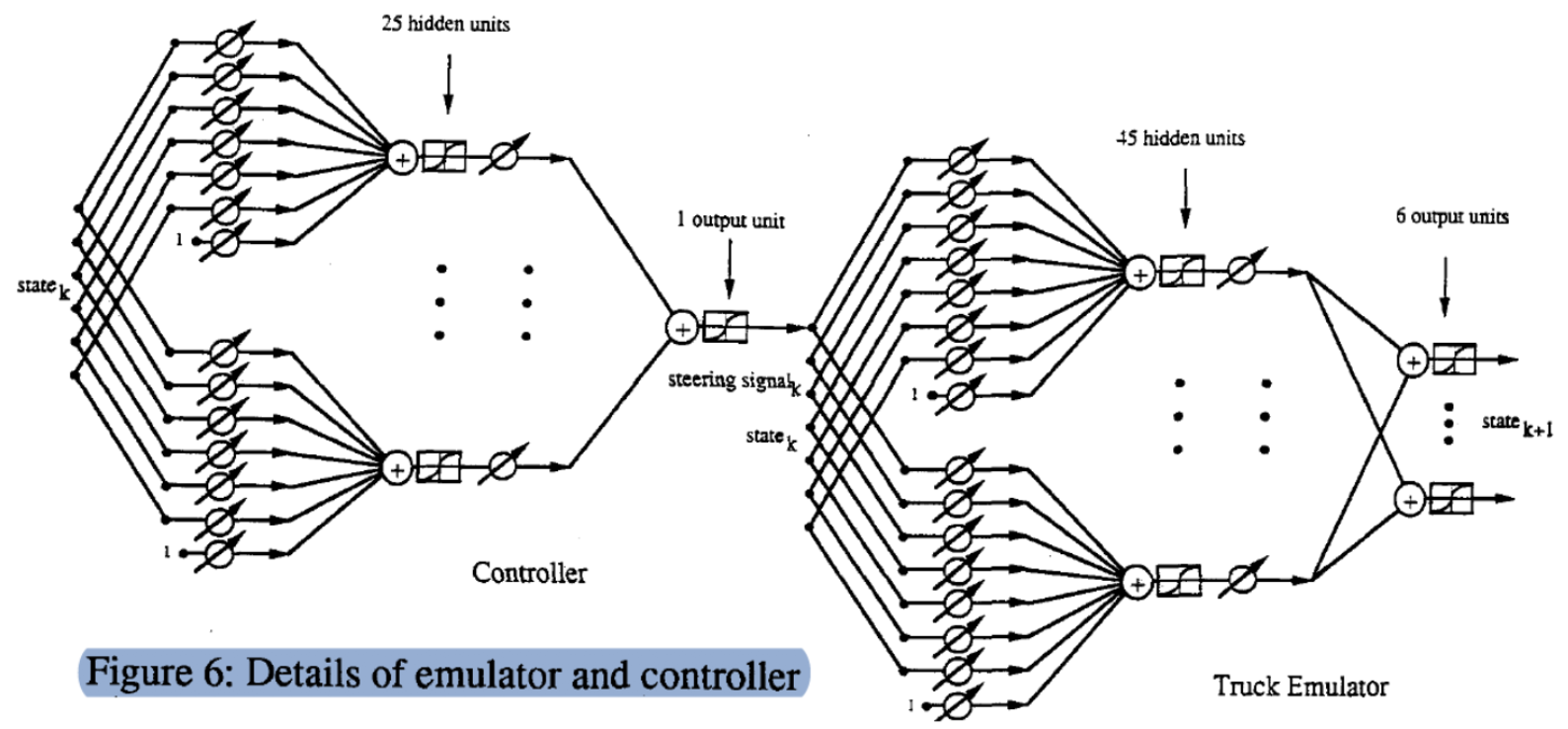
Questo è un grafico dettagliato del processo ($\matr{C}$, $\matr{T}$). Iniziamo con uno stato (vettore a 6 dimensioni), lo moltiplichiamo per una matrice di pesi addestrabili ottenendo 25 unità nascoste, che moltiplichiamo per un vettore di pesi addestrabili ad ottenere l’output (segnale di sterzo). Analogamente, passiamo lo stato e l’angolo $\phi$ (complessivamente un vettore di 7 dimensioni) attraverso due strati a produrre lo stato dell’intervallo successivo.

|

Per analizzare questo passaggio più nel dettaglio, mostriamo l’esatta implementazione dell’emulatore:

state_size = 6
steering_size = 1
hidden_units_e = 45

emulator = nn.Sequential(
    nn.Linear(steering_size + state_size, hidden_units_e),
    nn.ReLU(),
    nn.Linear(hidden_units_e, state_size)
)

optimiser_e = SGD(emulator.parameters(), lr=0.005)
criterion = nn.MSELoss()

Esempi di movimento

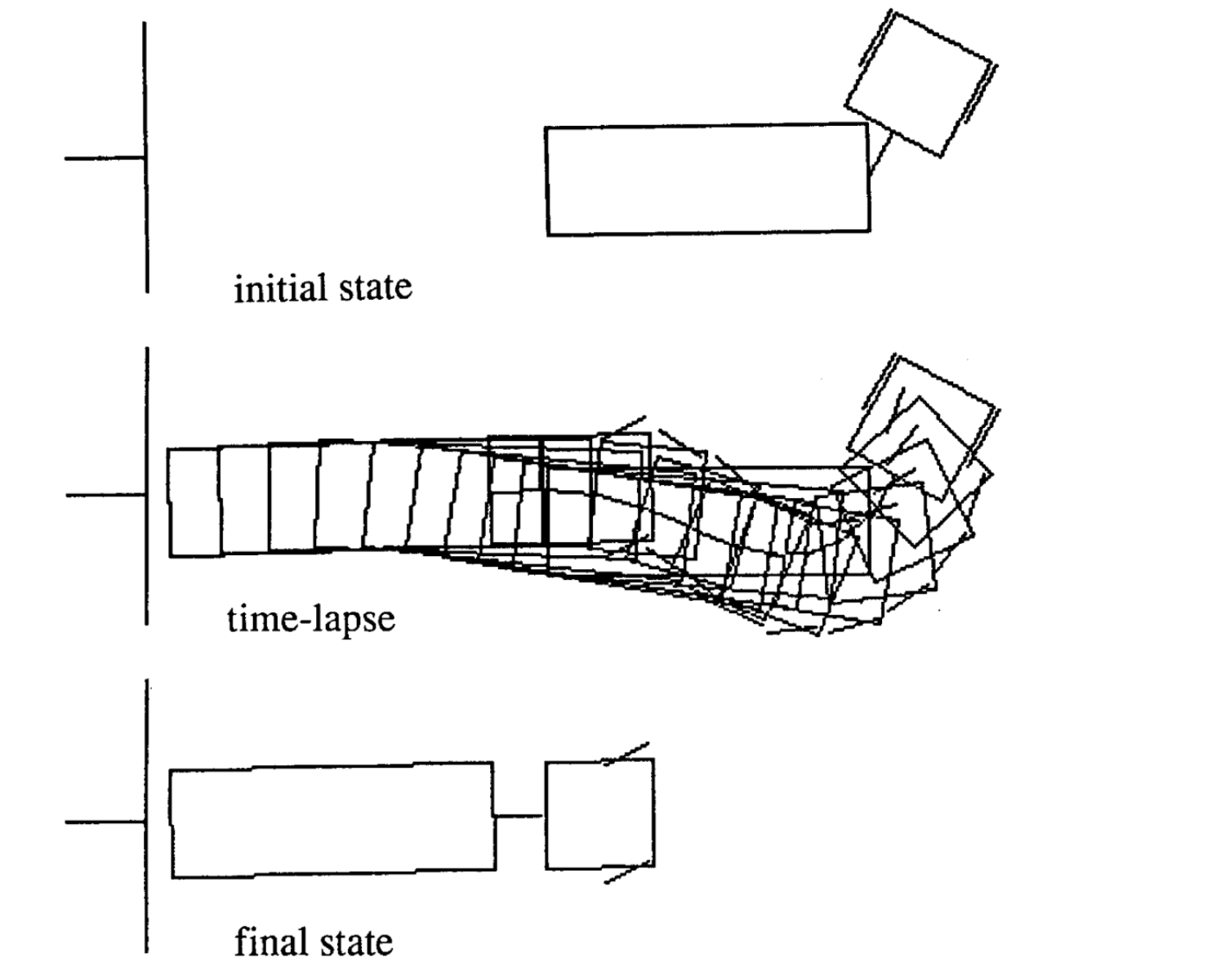
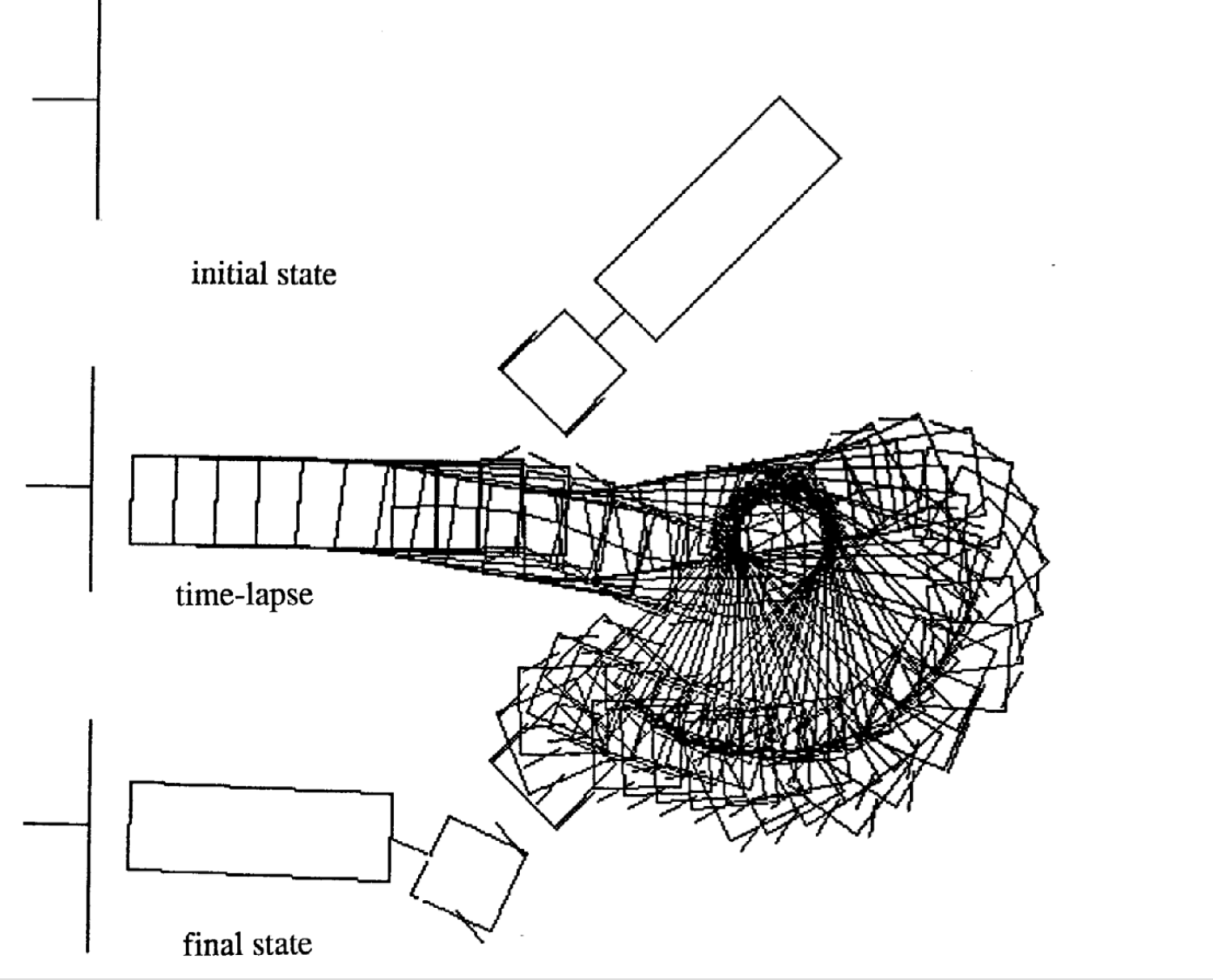
Di seguito vengono mostrati quattro esempi di movimento per stati iniziali differenti. Si noti che il numero d’intervalli temporali di ogni episodio non è fisso.

Fig. 7: esempi di movimento per quattro differenti stati iniziali

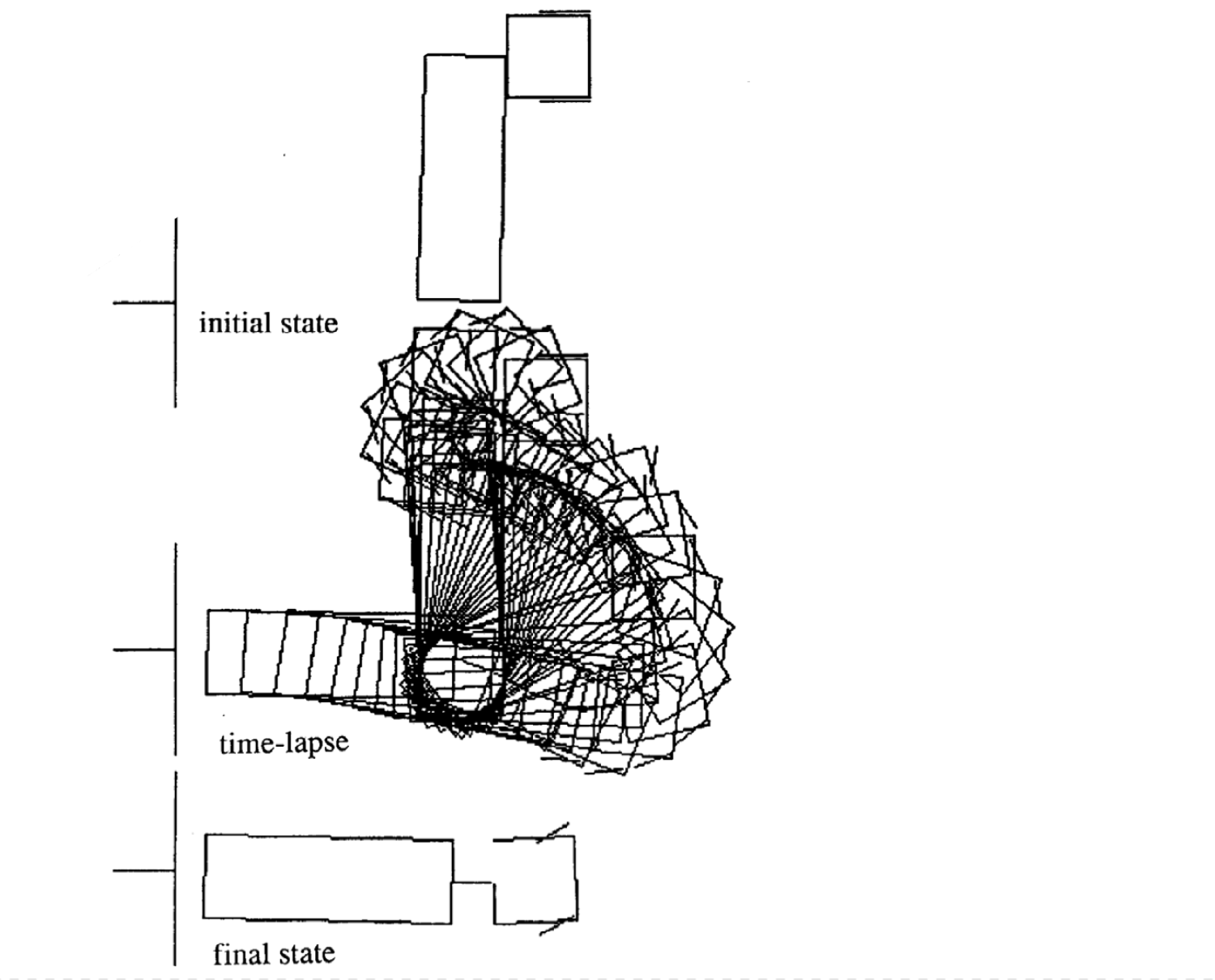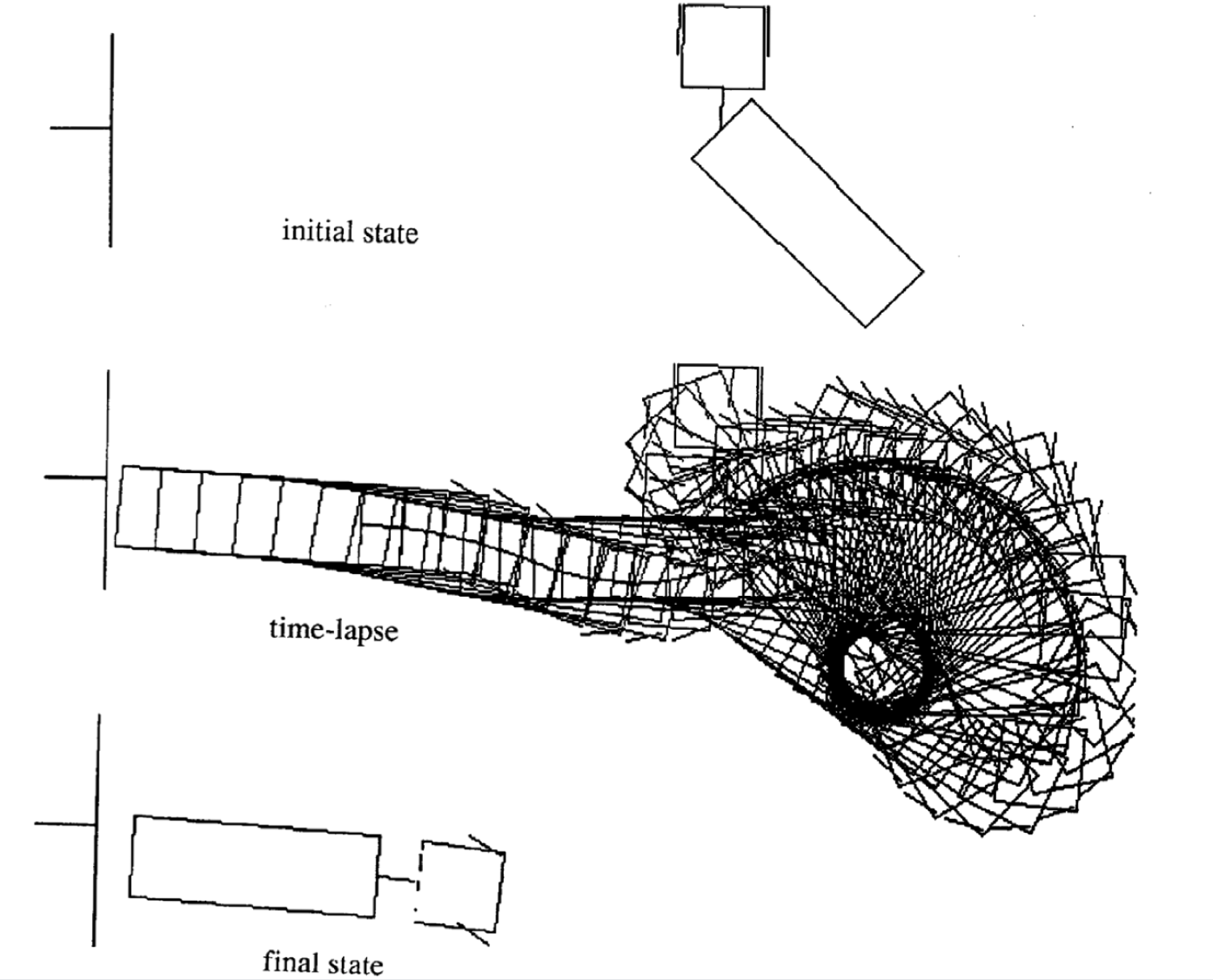Ulteriori risorse:

Una demo funzionante è reperibile all’indirizzo https://tifu.github.io/truck_backer_upper/. Si dia un’occhiata anche al codice, che può essere trovato qui https://github.com/Tifu/truck_backer_upper.