Apprendimento auto-supervisionato - ClusterFit e PIRL

Cosa manca nei compiti di pretesto? La speranza della generalizzazione

I compiti di pretesto generalmente sono composti da delle fasi di pre-addestramento che sono auto-supervisionate, dopodiché abbiamo i nostri compiti di trasferimento che sono spesso o di classificazione o di riconoscimento. Si spera che i compiti di pre-addestramento e di trasferimento siano “allineati”, ovvero la risoluzione dei compiti di pretesto aiuti sufficientemente bene nella risoluzione dei compiti di trasferimento. Di conseguenza, una buona parte della ricerca si concentra nella progettazione di compiti di pretesto e nella loro accurata implementazione.

Tuttavia, è molto incerto il meccanismo con il quale l’effettuazione di un compito non-semantico dovrebbe produrre buone caratteristiche. Per esempio, per quale motivo dovremmo aspettarci di imparare qualcosa nel campo semantico mentre risolviamo qualcosa come il Puzzle (Jigsaw)? Oppure, per quale motivo ci si dovrebbe attendere che la “previsione degli hashtag” dalle immagini dovrebbe in qualche modo aiutare l’addestramento di un classificatore su compiti di trasferimento? Di conseguenza, la questione permane: come si devono progettare dei buoni compiti di pre-addestramento che siano in linea con i compiti di trasferimento?

Si può “misurare” questo problema andando ad analizzare le rappresentazioni degli strati (si faccia riferimento alla Fig. 1). Se le rappresentazioni dell’ultimo strato non sono ben allineate con il compito di trasferimento, allora potrebbe darsi che il compito di pretesto non sia ben in linea con il compito da risolvere.

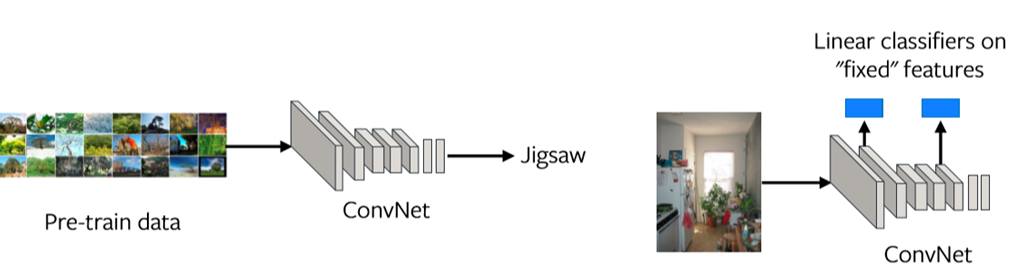
Fig. 1: rappresentazioni delle caratteristiche in ogni strato

In Fig.2 è presente un grafico con la media della precisione media (Mean Average Precision) ad ogni strato per classificatori lineari sul dataset VOC07 utilizzando il pre-addestramento del Puzzle. È chiaro che l’ultimo strato è molto specializzato per il problema del Puzzle.

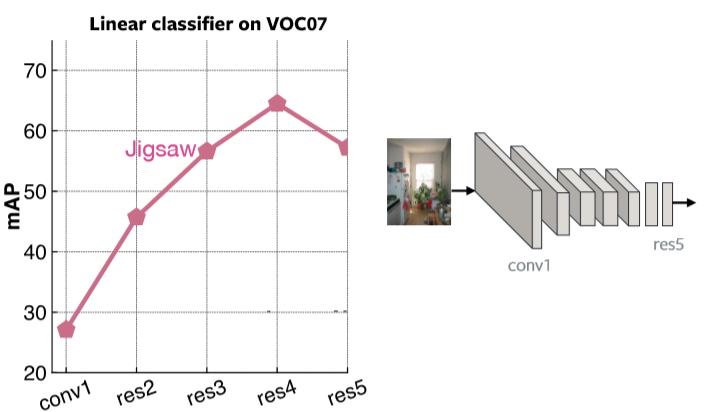
Fig. 2: performance del puzzle sulla base di ogni strato

Che cosa vogliamo ottenere dalle caratteristiche pre-addestrate?

• Rappresentare come le immagini si relazionano fra di loro

  • ClusterFit: migliorare la generalizzazione delle rappresentazioni visive

• Essere robusti a “parametri di disturbo” – Invarianza Ad esempio: invarianza alla posizione degli oggetti, all’illuminazione, ai colori esatti

  • PIRL: apprendimento auto-supervisionato di rappresentazioni invarianti al pretesto (PIRL, Pre-text Invariant Representations Learning)

Due opzioni per apprendere le proprietà sopra descritte sono il Clustering e l’Apprendimento Contrastivo. Hanno iniziato a performare molto meglio di qualsiasi compito di pretesto progettato finora. Un metodo che appartiene al clustering è ClusterFit, mentre PIRL appartiene alla sfera delle invarianze.

ClusterFit: migliorare la generalizzazione delle rappresentazioni visive

Partizionare lo spazio delle caratteristiche è un modo per vedere come le immagini si relazionano fra di loro.

Il metodo

ClusterFit segue due passaggi. Uno è il passaggio di partizione, l’altro è quello di previsione.

Clustering: partizionamento delle caratteristiche

Consideriamo una rete pre-addestrata (Pre-trained Network) e la usiamo per estrarre un gruppo di caratteristiche da un insieme d’immagini. Viene quindi applicato, su queste caratteristiche, un partizionamento utilizzando K-means, in modo tale che ogni immagine appartenga a uno e un solo cluster, il quale assume il ruolo di categoria (etichetta) dell’immagine stessa.

Fig. 3: passaggio di partizione o *clustering*

Previsione: predire l’assegnamento al cluster

Per questo passaggio, addestriamo una rete da zero (“from scratch”). Il suo compito è quello di prevedere la categoria di assegnazione delle immagini. Queste categorie, chiamate “pseudo-etichette” (pseudo-labels), sono quelle che abbiamo ottenuto nella prima fase attraverso il clustering.

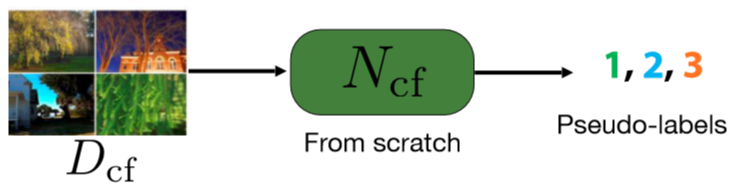
Fig. 4: passaggio di previsione

Un compito di pre-addestramento e trasferimento consiste, prima di tutto, nel pre-addestramento di una rete e nella sua successiva valutazione in un compito downstream (ovvero, un compito che la rete pre-addestrata non è stata addestrata a risolvere), come mostrato nella prima riga della Fig. 5. ClusterFit compie il pre-addestramento su un dataset $D_{cf}$ ad ottenere la rete pre-addestrata $N_{pre}$, le cui rappresentazioni vengono estrapolate per generare i cluster. Successivamente, s’impara una nuova rete $N_{cf}$ da zero su questi dati. Infine, utilizziamo $N_{cf}$ per tutti i compiti downstream.

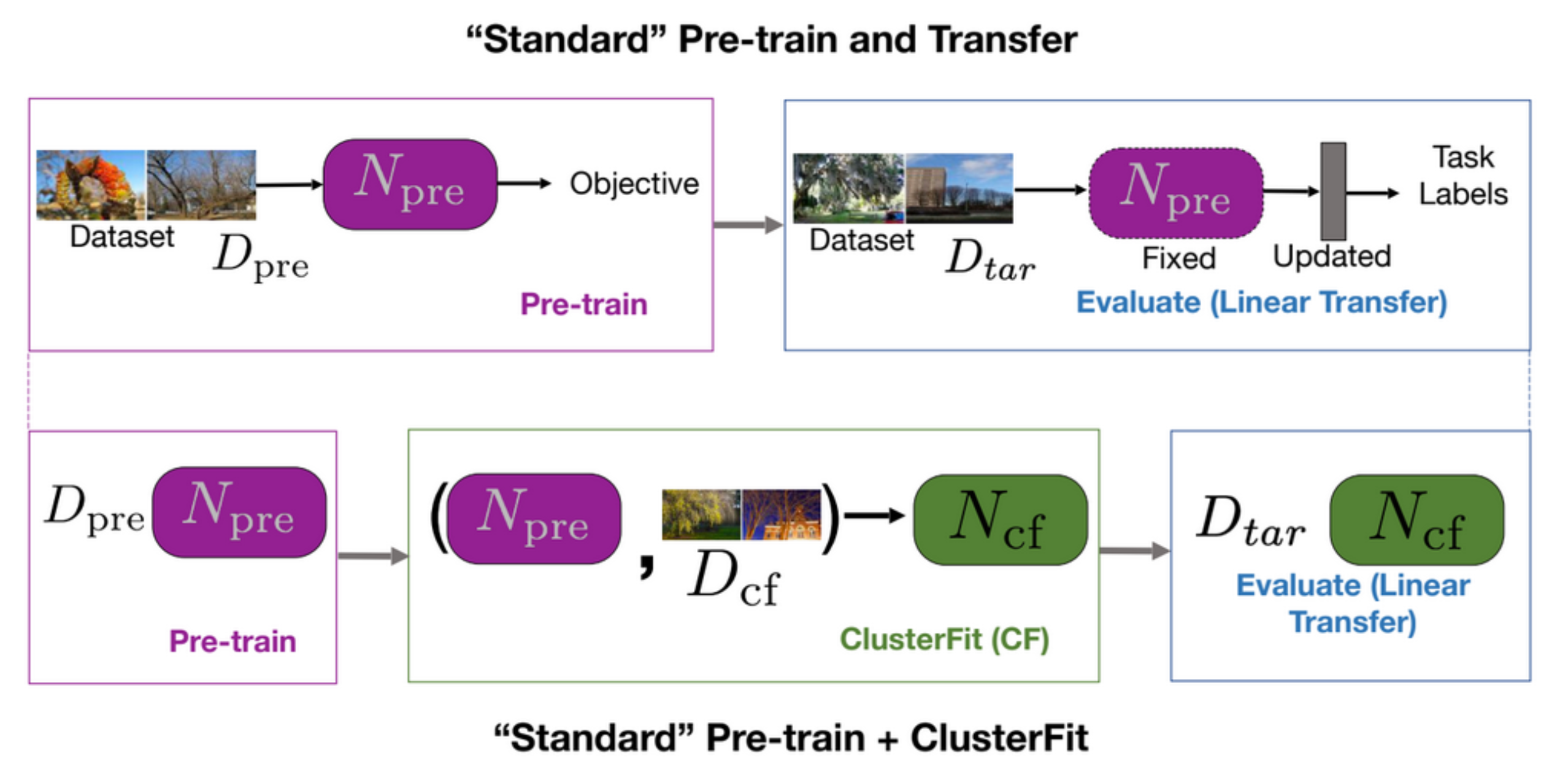
Fig. 5: pre-addestramento "classico" VS. pre-addestramento "classico" + ClusterFit

Perche ClusterFit funziona

Il motivo per cui ClusterFit funziona è che il passaggio di clustering cattura solo le informazioni essenziali, mentre gli artefatti sono scartati, facendo sì che la seconda rete apprenda qualcosa di leggermente più generico.

Per capire questo punto, si opera un esperimento piuttosto semplice. Aggiungiamo del rumore a ImageNet-1K e addestriamo una rete sulla base di questo dataset. Dopodiché, valutiamo le rappresentazioni delle caratteristiche estratte da questa rete su un compito downstream, come ImageNet-9K. Come si può notare dalla Fig. 6, aggiungiamo svariati livelli di rumore ad ogni categoria (label noise) di ImageNet-1K e valutiamo la performance di trasferimento (transfer) di diversi metodi su ImageNet-9K.

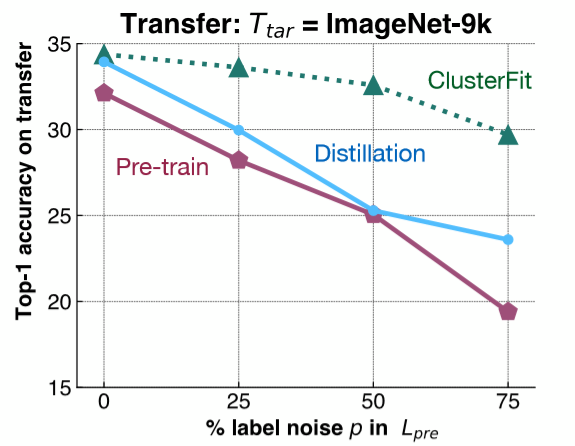
Fig. 6: esperimento di controllo

La linea rosa mostra la performance della rete pre-addestrata. La performance diminuisce all’aumentare del rumore. La linea blu rappresenta la distillazione (distillation) del modello, ovvero utilizziamo la rete iniziale e la utilizziamo per generare le etichette. La distillazione normalmente offre migliori performance rispetto alla rete pre-addestrata. La rete verde, rappresentante ClusterFit, è costantemente più alta rispetto alle altre due. Questi risultati validano la nostra ipotesi.

• Domanda: perché comparare utilizzando la distillazione? Qual è la differenza fra la distillazione e ClusterFit?

Nella distillazione consideriamo la rete pre-addestrata e usiamo le etichette che la rete ha predetto in una maniera più “tollerante” per generare etichette per le nostre immagini. Ad esempio, otteniamo una distribuzione su tutte le classi e usiamo questa distribuzione per addestrare la seconda rete. La distribuzione più permissiva aiuta a potenziare le classi iniziali a disposizione. In ClusterFit ignoriamo completamente lo spazio delle etichette (degli output).

Performance

Applichiamo questo metodo all’apprendimento auto-supervisionato. Qui dal metodo del Puzzle otteniamo la rete pre-addestrata $N_{pre}$ che poi utilizzeremo per ClusterFit. Dalla Fig. 7 vediamo che la performance di trasferimento su diversi dataset mostra un ammontare piuttosto sorprendente di guadagno in accuratezza rispetto ad altri metodi auto-supervisionati.

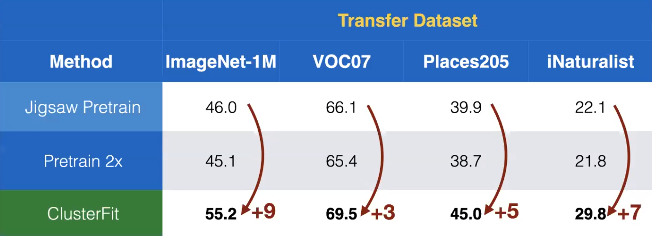
Fig. 7: performance di trasferimento su diversi dataset

ClusterFit funziona su ogni rete pre-addestrata. Esempi di guadagno senza utilizzo ulteriore di dati, etichette o variazioni architettoniche possono essere visualizzati in Fig. 8. In un certo senso, potremmo pensare a ClusterFit come un metodo auto-supervisionato di affinamento (fine-tuning), a migliorare la qualità delle rappresentazioni.

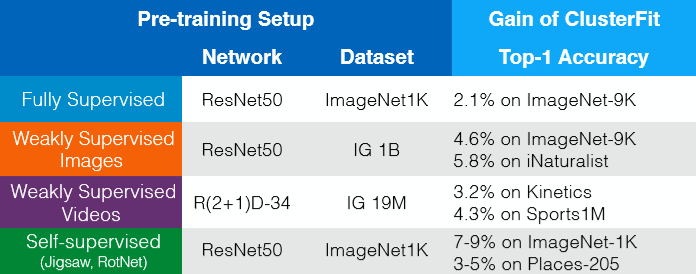
Fig. 8: guadagni in performance (*gains*) senza utilizzo di dati, etichette o variazioni architettoniche aggiuntivi

Apprendimento auto-supervisionato di rappresentazioni di pretesto invarianti (PIRL)

Apprendimento contrastivo (Contrastive Learning)

In parole povere, l’apprendimento contrastivo è un framework generico per imparare uno spazio delle caratteristiche che possa avvicinare punti mutuamente correlati, allontanando contemporaneamente quelli che non lo sono.

Fig. 9: gruppi d'immagini mutuamente correlate e non correlate

In questo caso, s’immagini che i rettangoli della stessa tonalità siano mutuamente correlati (blu con blu, verdi con verdi, viola con viola).

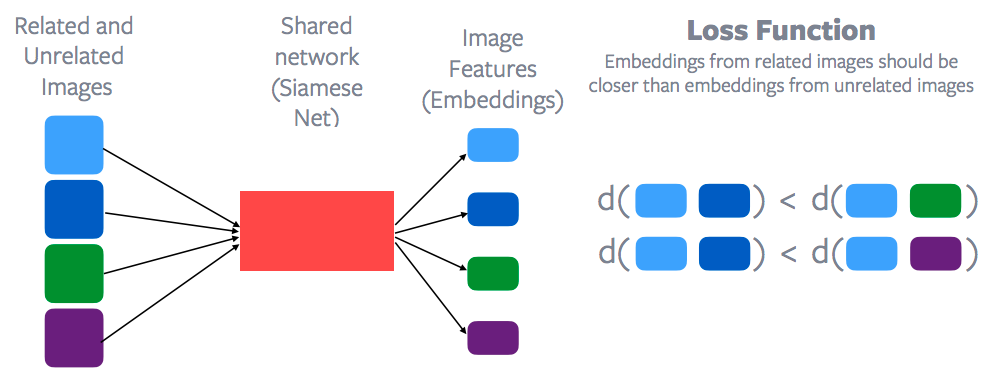
Fig. 10: apprendimento contrastivo e funzione di perdita

Le caratteristiche di ognuno di questi punti vengono estratte attraverso una rete condivisa (shared network) chiamata rete siamese (Siamese Network). Dopodiché, viene applicata una funzione di perdita contrastiva per provare a minimizzare la distanza fra i punti delle due categorie blu, anziché quella fra, ad esempio, una delle due categorie blu e una delle due categorie verdi. Detto in altre parole, la distanza fra le due categorie blu dovrebbe essere inferiore alla distanza fra i punti blu e i punti verdi o viola. Così facendo, lo spazio di proiezione di istanze correlate dovrebbe essere più vicino rispetto alle istanze non correlate. Questa è l’idea generale dell’apprendimento contrastivo e, naturalmente, Yann LeCun è stato uno dei primi professori a proporre questo metodo. Questa disciplina sta attraversando un periodo di rinascita nel campo dell’apprendimento auto-supervisionato, tant’è che tanti metodi allo stato dell’arte di questa categoria sono basati sull’apprendimento contrastivo.

Come definire la mutua correlazione?

La principale questione è la definizione di mutua (non) correlazione. Nel caso di apprendimento supervisionato è chiaro che tutte le immagini, ad esempio, di cani sono correlate e qualsiasi immagine che non rappresenti un cane è incorrelata con quelle di cani. Non è tuttavia molto chiaro come definire la correlazione e la non correlazione nel caso dell’apprendimento auto-supervisionato. L’altra differenza principale rispetto ad un compito di pretesto è che l’apprendimento contrastivo ragiona in termini di grosse moli di dati passate al vaglio contemporaneamente. Se si osserva la funzione di perdita, questa coinvolge sempre più di un’immagine. Come da Fig. 10, nella prima riga considera le immagini dalle categorie blu e verdi, mentre nella seconda riga passa in consegna quelle dalle categorie blu e viola. Tuttavia, se si esamina un compito come il Puzzle o la Rotazione, si ragiona sempre al livello delle singole immagini considerate in maniera indipendente dalle altre. Questa è un’altra differenza dell’apprendimento contrastivo: quest’ultimo ragiona in termini di più dati presi in rassegna contemporaneamente.

Si potrebbero utilizzare tecniche simili rispetto a quanto discusso prima: frame di video o altri dati di natura sequenziale. Frame di un video che sono vicini dal punto di vista dell’ordine temporale si possono considerare come correlati, ad esempio, rispetto a frame lontani nel tempo; ciò ha posto le fondamenta di una miriade di metodi di apprendimento auto-supervisionato in quest’area. Questo metodo viene chiamato CPC (codificazione predittiva contrastiva, Contrastive Predictive Coding); esso si basa sulla natura sequenziale di un segnale e, sostanzialmente, assume che le istanze ravvicinate dal punto di vista sequenziale (ad esempio, spazio-temporale) siano correlate, mentre quelle distanti, secondo lo stesso criterio, siano incorrelate. Un grosso numero di lavori sfrutta quest’assunzione: si può lavorare sia nel campo audio, video, testuale, o particolari tipi d’immagine. E recentemente, abbiamo iniziato a lavorare su pezzi di video e audio considerati assieme: la traccia video e la sua traccia audio corrispondente sono istanze correlate, mentre una traccia video ed una audio provenienti da pezzi diversi sono istanze incorrelate.

Tracciamento di oggetti

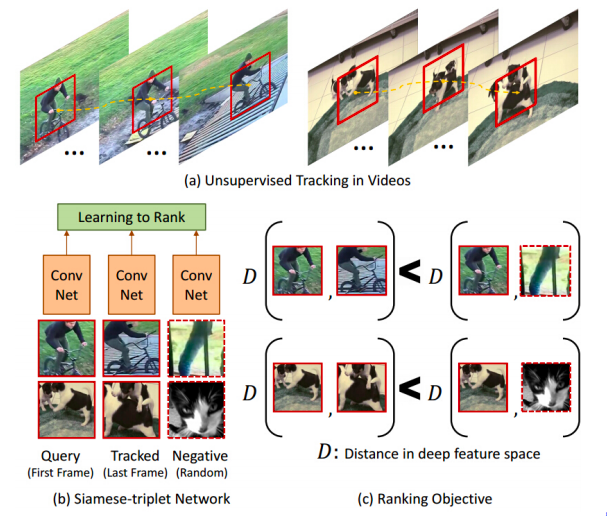
Fig. 11: tracciamento di oggetti

Una parte dei lavori iniziale dell’apprendimento auto-supervisionato utilizza anch’esso le nozioni di apprendimento contrastivo. Questi lavori definiscono la nozione di istanze correlate in maniera piuttosto interessante. Si fa girare un tracciatore di oggetti su di un video: questo definisce una finestra mobile che segue determinati oggetti; si assume dunque che il contenuto iniziale di questa finestra è correlato al contenuto della finestra stessa, opportunamente mossa dal tracciatore, negli istanti successivi; si assume invece che non vi sia correlazione fra questa finestra e quelle di tracce video separate.

Porzioni d’immagine vicine vs. lontane

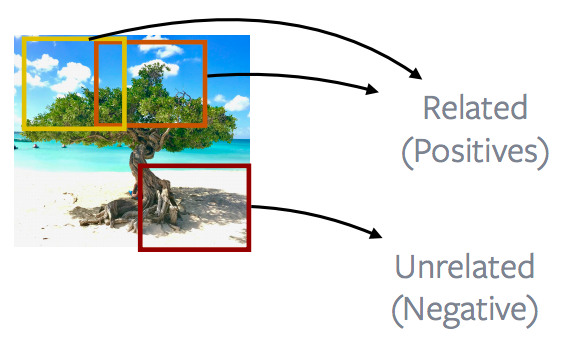
Fig. 12: porzioni (finestre) d'immagine vicine vs. porzioni d'immagine lontane

Generalmente, quando si parla d’immagini, una buona parte del lavoro viene speso nell’osservazione di porzioni (o finestre) d’immagine vicine e la contrapposizione con quelle lontane; molti metodi CPC di prima o seconda generazione di fatto sfruttano questa proprietà delle immagini. Le finestre vicine sono chiamate positive (Positives), mentre finestre lontane si traducono in negative (Negatives); l’obiettivo è minimizzare la perdita contrastiva usando queste definizioni di positività e negatività.

Porzioni provenienti da un’immagine vs. provenienti da altre immagini

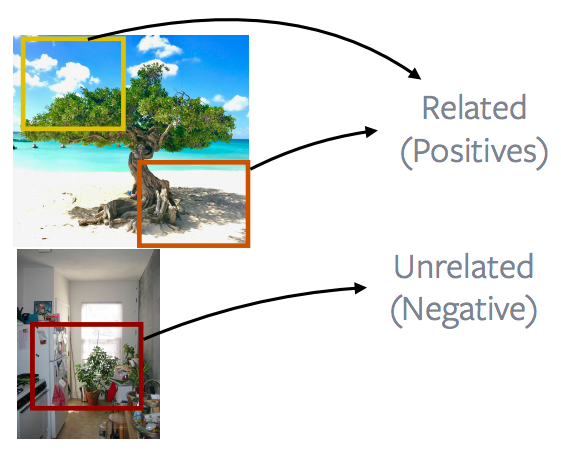
Fig. 13: porzioni di un'immagine vs. porzioni di altre immagini

Il metodo più popolare e performante di confrontare immagini diverse è considerare porzioni/finestre da un’immagine e metterle in contrasto con porzioni di un’altra immagine. Ciò forma le fondamenta di una serie di metodi popolari come discriminazione d’istanze, MoCo, PIRL, SimCLR. L’idea di base è di lavorare su quanto è mostrato nell’immagine. Andando nel dettaglio, questi metodi estraggono delle finestre casuali da un’immagine. Queste finestre possono essere sovrapposte, una contenuta dentro l’altra o completamente disgiunte; dopodiché, vi si applica qualche metodo di aumento dei dati, come variazioni o rimozione del colore, ad esempio. Dopodiché, si assume che queste due finestre siano positive. Un’altra finestra viene estratta casualmente da un’immagine differente; di nuovo, questa diviene un esempio negativo. Si estraggono molti di questi esempi e sostanzialmente si esegue un apprendimento contrastivo. Abbiamo due istanze positive, ma ce ne sono molte di negative con cui compiere l’apprendimento contrastivo.

Principio sottostante i compiti di pretesto

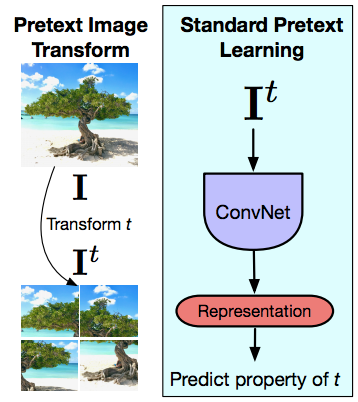
Fig. 14: trasformazione di pretesto dell'immagine e apprendimento di pretesto standard

Ora ci avviciniamo un po’ di più a PIRL provando a comprendere qual è la differenza principale rispetto ai compiti di pretesto e come l’apprendimento contrastivo si distacca da questi ultimi. Di nuovo, i compiti di pretesto ragionano in termini di una singola immagine alla volta. L’idea è che, data un’immagine ed una precedente trasformazione di quest’ultima (in questo caso una trasformazione di tipo Puzzle), si dà in pasto questa immagine ad una rete convoluzionale e si provano a prevedere le proprietà della trasformazione (permutazione, rotazione, variazione/rimozione del colore) che è stata applicata. Il compito di pretesto ragiona sempre in termini di una singola immagine. Il secondo punto è che il compito che si sta svolgendo in questo caso deve cogliere delle proprietà della trasformazione, ovvero la vera permutazione o il tipo di rotazione applicate; ciò significa che la rappresentazione fornita dall’ultimo strato della rete (rappresentazioni che verranno fornite a PIRL) potrebbero variare parecchio al variare delle trasformazioni, e questa è una limitazione progettuale, in quanto si tratta di risolvere un compito specifico. Sfortunatamente, ciò significa che la rappresentazione prodotta dall’ultimo strato cattura proprietà di bassissimo livello del segnale, ovvero concetti come rotazioni, laddove ciò che ci aspettiamo da queste rappresentazioni è che siano invarianti a queste proprietà, e che siano capaci di riconoscere concetti come un gatto, indipendentemente se quest’ultimo è dritto su quattro zampe, oppure piegato di 90 gradi verso un lato. Quando invece si vuole apprendere uno specifico compito di pretesto, si sta imponendo alla rete l’esatto opposto, ovvero che essa dovrebbe essere in grado di riconoscere se un’immagine sia “dritta” o “piegata di lato”. Ci sono molte eccezioni in cui si vuole che di fatto al rete sia co-variante a queste rappresentazioni di basso livello, e ciò dipende molto dal tipo di compito con cui si sta lavorando e molti compiti in 3D devono essere di tipo predittivo. Si vuole quindi predire che trasformazioni la videocamera può apportare, ad esempio, quando si sta comparando due prospettive dello stesso oggetto. Tuttavia, finché si considerano applicazioni di molti compiti di natura semantica, si vuole in realtà essere covarianti alle trasformazioni applicate all’input.

Quanto importante è l’invarianza?

L’importanza è stata la parola chiave dell’apprendimento di caratteristiche, come nell’esempio di SIFT, metodo “artigianale” per apprendere caratteristiche invarianti alla traslazione e alla scalatura. Le reti supervisionate, come AlexNet, sono addestrate ad essere invarianti all’aumento dei dati. Si vuole che queste reti classifichino diversi ritagli o rotazioni dell’immagine, piuttosto che predire quale specifica trasformazione vi sia stata applicata.

PIRL

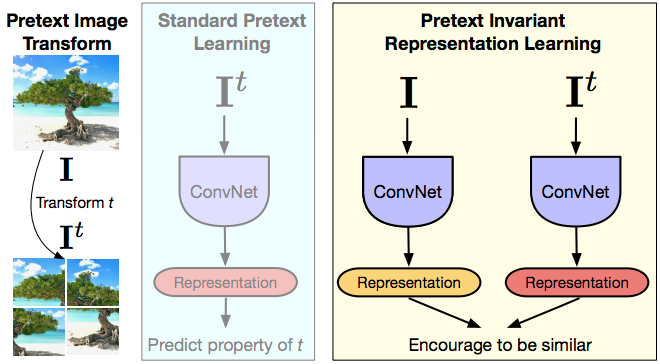
Fig. 15: PIRL

Ciò ha ispirato PIRL. L’acronimo sta per Pretext Invariant Representation Learning (apprendimento delle rappresentazioni invariante al pretesto): l’idea è che si vuole che le rappresentazioni siano invarianti a trasformazioni dell’input, ovvero catturino la più piccola informazione possibile relativamente a queste trasformazioni. Si ha un’immagine, ne si considera una trasformazione, si danno entrambe queste immagini come input di una rete convoluzionale, si ottengono due rappresentazioni e si forzano queste a essere simili. In termini più formali, l’immagine $I$ e ogni versione trasformata da compiti di pretesto $I^t$ sono istanze correlate; ogni altra immagine rappresenta un’istanza non correlata. Così facendo, si spera che le rappresentazioni ottenute tramite la rete contengano un’informazione minimale riguardo alla trasformazione $t$. Assumiamo di utilizzare l’apprendimento contrastivo. Ciò consiste nel considerare le caratteristiche $v_I$ provenienti dall’immagine originaria $I$ e considerare le caratteristiche $v_{I^t}$ della versione trasformata: si vuole che entrambe queste rappresentazioni siano identiche. Nella precedente lezione abbiamo imparato due metodi allo stato dell’arte delle trasformazioni di pretesto, il Puzzle e il metodo di Rotazione. In un certo senso, questo è un apprendimento a più compiti (multitask learning), ma non stiamo cercando di predire entrambe le trasformazioni, stiamo cercando di esserne invarianti.

Utilizzo di un gran numero di negativi

Il concetto chiave che ha reso possibile il buon funzionamento dell’apprendimento contrastivo in passato è l’utilizzo di un grosso numero di esempi negativi. Uno dei paper che ha introdotto questo concetto è il paper sulla discriminazione delle istanze del 2018, che ha introdotto il concetto di “banco di memoria” (memory bank). Molti metodi allo stato dell’arte ruotano attorno all’idea del banco di memoria. Quest’ultimo rappresenta un modo carino di ottenere un grosso numero di negativi senza realmente richiedere un incremento della potenza computazionale. Si salva in memoria un vettore delle caratteristiche per immagine e si utilizza questo vettore nell’apprendimento contrastivo.

Come funziona

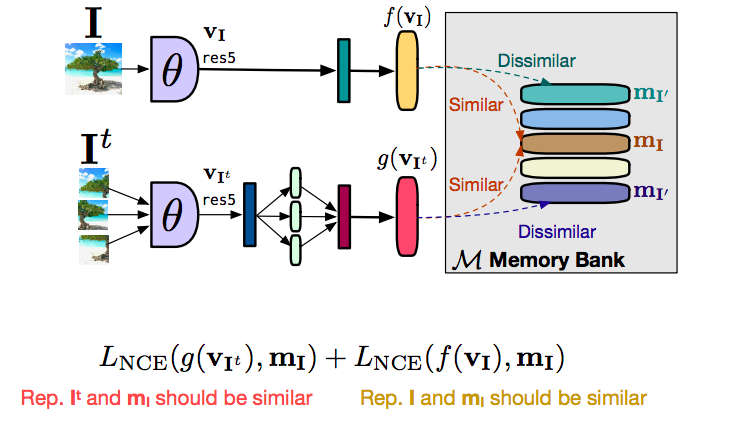
Fig. 16: come funziona il banco di memoria

Prima di tutto, parliamo di come si effettuerebbe il setup di PIRL senza l’utilizzo di un banco di memoria. Si consideri un’immagine $I$ e un’immagine $I^t$, si diano in input entrambe alla rete ad ottenere un vettore delle caratteristiche $f(v_I)$ dall’immagine originaria $I$ e un vettore delle caratteristiche $g(v_I)$ dalla trasformata, in questo caso le porzioni d’immagine. Si vuole ottenere che le caratteristiche $f$ e $g$ siano simili, e che, al contempo, le caratteristiche di ogni altra immagine non correlata siano dissimili. In tal caso, ciò che possiamo fare è: se necessitiamo molti esempi negativi, si vuole che un numero molto alto di immagini negative venga dato contemporaneamente dato in input alla rete, con la conseguenza che la grandezza del batch diviene veramente molto grande, il che non è un aspetto del tutto positivo, soprattutto se la memoria della GPU è limitata. Possiamo ovviare a ciò tramite l’utilizzo di un c.d. banco di memoria. Esso conserva un vettore delle caratteristiche per ogni immagine del dataset. Quando, ad esempio, si necessita di applicare l’apprendimento contrastivo, sarà necessario semplicemente recuperare questo vettore dalla memoria, ricavando le caratteristiche delle immagini incorrelate. Dividendo l’obiettivo in due parti, c’è un termine contrastivo per rendere l’immagine trasformata $g(v_I)$ simile alla rappresentazione che abbiamo in memoria, $m_I$. E, in maniera analoga, abbiamo una seconda rete convoluzionale contrastiva che cerca di rendere $f(v_I)$ simile alla rappresentazione in memoria. Essenzialmente, $g$ ed $f$ vengono entrambe “tirate” verso $m_I$, ovvero vengono rese simili fra di loro. La suddivisione dell’obiettivo in queste due parti, piuttosto che applicare direttamente l’apprendimento contrastivo fra $f$ e $g$, permette una stabilizzazione dell’addestramento.

Il pre-addestramento di PIRL

Si tratta di una configurazione standard per la valutazione del pre-addestramento. Per l’apprendimento per trasferimento, si può pre-addestrare sulle immagini senza annotazioni. Il modo classico per fare ciò è prendere una rete pre-addestrata su immagini, eliminare le annotazioni e lavorare come se si trattase di un apprendimento non-supervisionato.

Valutazione

Si può quindi valutare il tutto tramite, ad esempio, un fine-tuning pieno oppure addestrando un classificatore lineare. Secondariamente, si testa PIRL e la sua robustezza alla distribuzione delle immagini addestrandolo ad immagini “allo stato brado”: si prendono, ad esempio, 1 milione d’immagini scelte a caso da Flickr (dataset YFCC), si effettua un pre-addestramento su queste immagini e si “trapianta” su dataset diversi.

Valutazione su compiti di riconoscimento di oggetti

PIRL è stato prima di tutto valutato su compiti di riconoscimento di oggetti (un compito standard nella visione artificiale) e si è comportato meglio delle reti pre-addestramente in maniera supervisionata su ImageNet, sia sul dataset VOC07+12 che su VOC07. Inoltre, PIRL ha dato migliori risultati persino nel criteri di valutazione più restrittivi, $AP^{all}$ e questo è un segnale positivo.

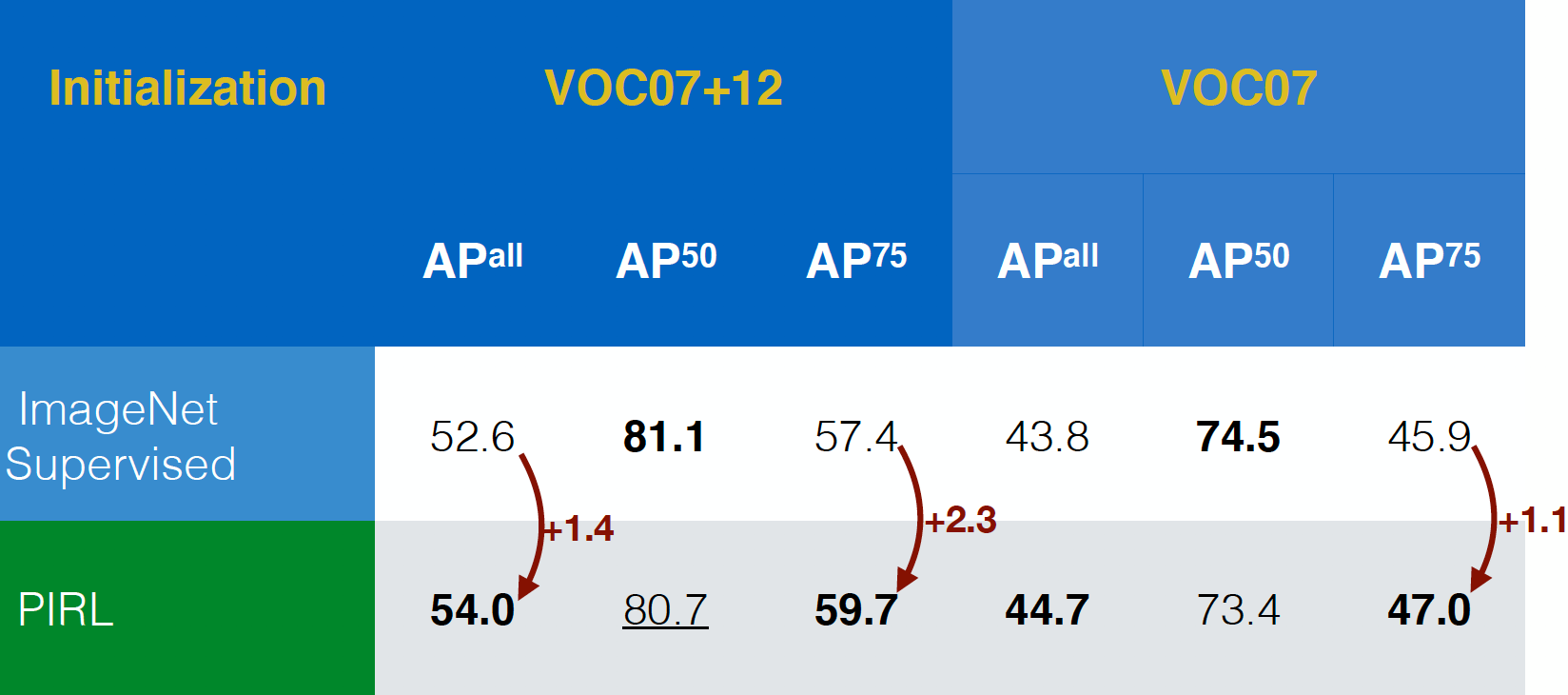
Fig. 17: performance nei compiti di riconoscimento di oggetti su diversi dataset

Valutazione su apprendimento auto-supervisionato

PIRL è stato valutato su compiti di apprendimento auto-supervisionato. Nuovamente, si è comportato piuttosto bene, persino meglio dei compiti di pretesto come il Puzzle. La sola differenza è che PIRL è una versione invariante (rispetto a determinate trasformazioni), mentre il Puzzle ne è covariante.

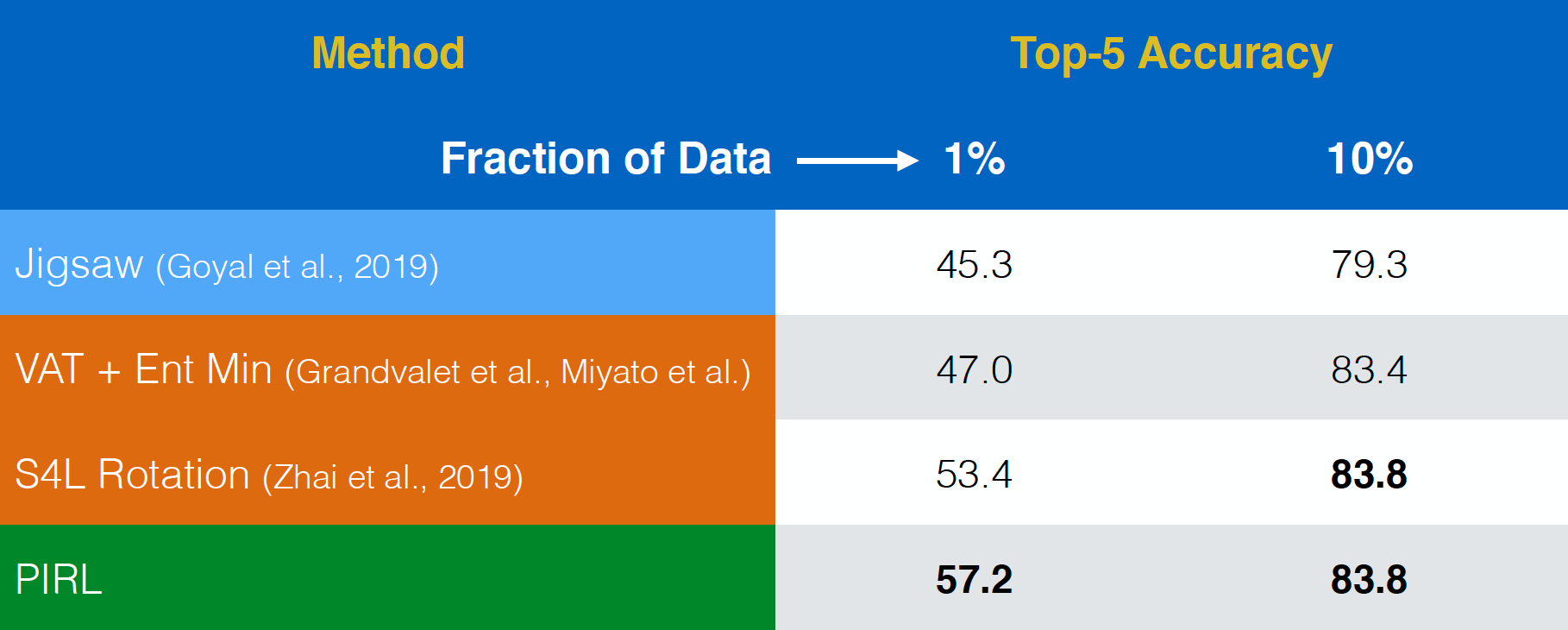
Fig. 18: apprendimento auto-supervisionato su ImageNet

Valutazione su un classificatore lineare

Quando PIRL è stato valutato su un classificatore lineare, le sue performance erano alla pari con CPCv2, quando questo è stato sviluppato. Funzionava bene anche con una serie di configurazioni dei parametri e con diverse architetture e, ovviamente, ora si possono ottenere performance decenti attraverso metodi come SimCLR o simili; infatti, l’accuratezza di SimCLR è attorno al 69-70%, mentre PIRL si attesta attorno al 63%.

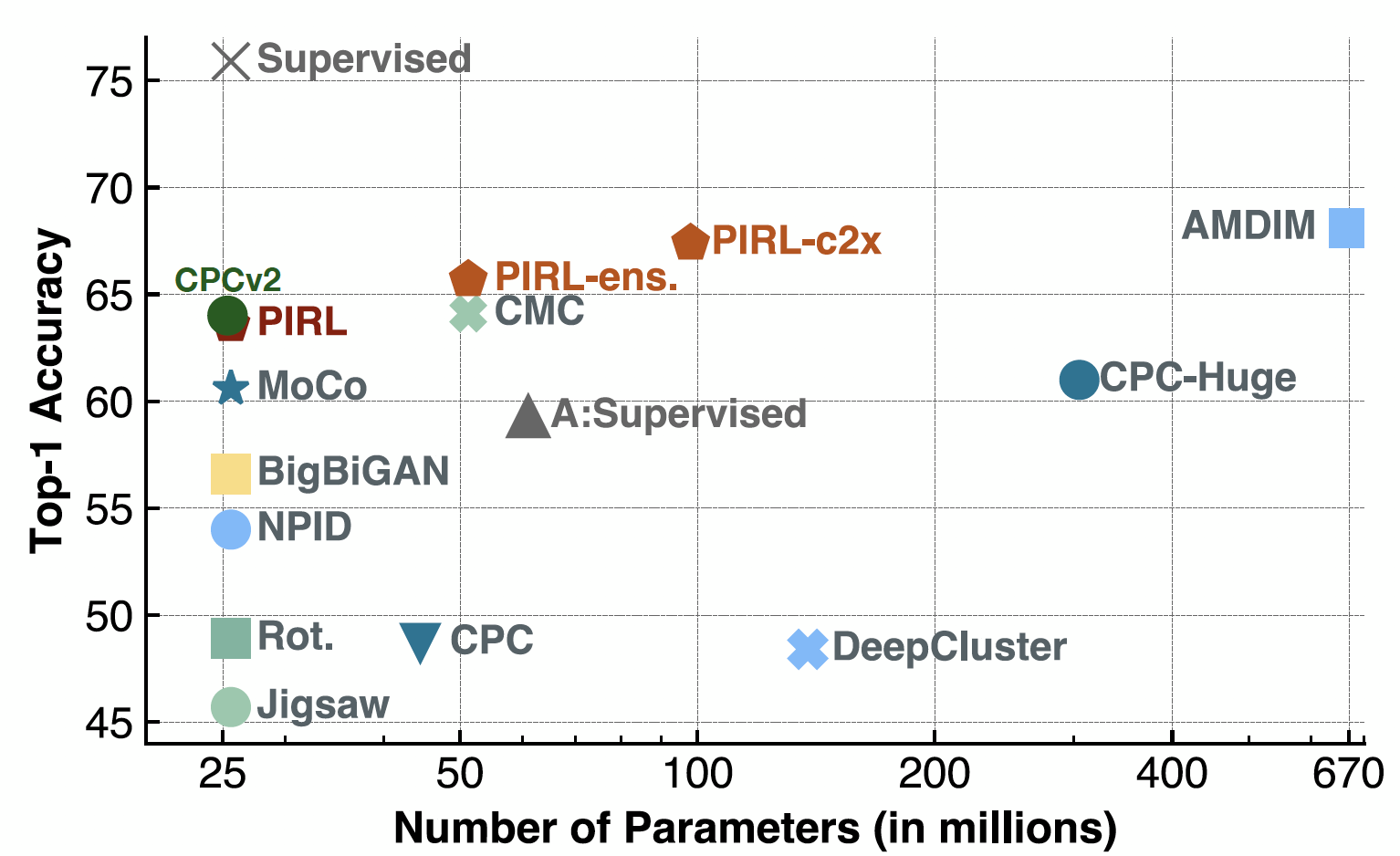
Fig. 19: classificazione su ImageNet con modelli lineari

Valutazione sulle immagini di YFCC

PIRL è stato valutato sulle immagini “allo stato brado” di Flickr dal dataset YFCC. È stato in grado di performare meglio del Puzzle, persino con dataset $100$ volte più piccoli. Ciò mostra la potenza di considerare l’invarianza per la rappresentazione nei compiti di pretesto, anziché prevedere semplicemente i compiti di pretesto.

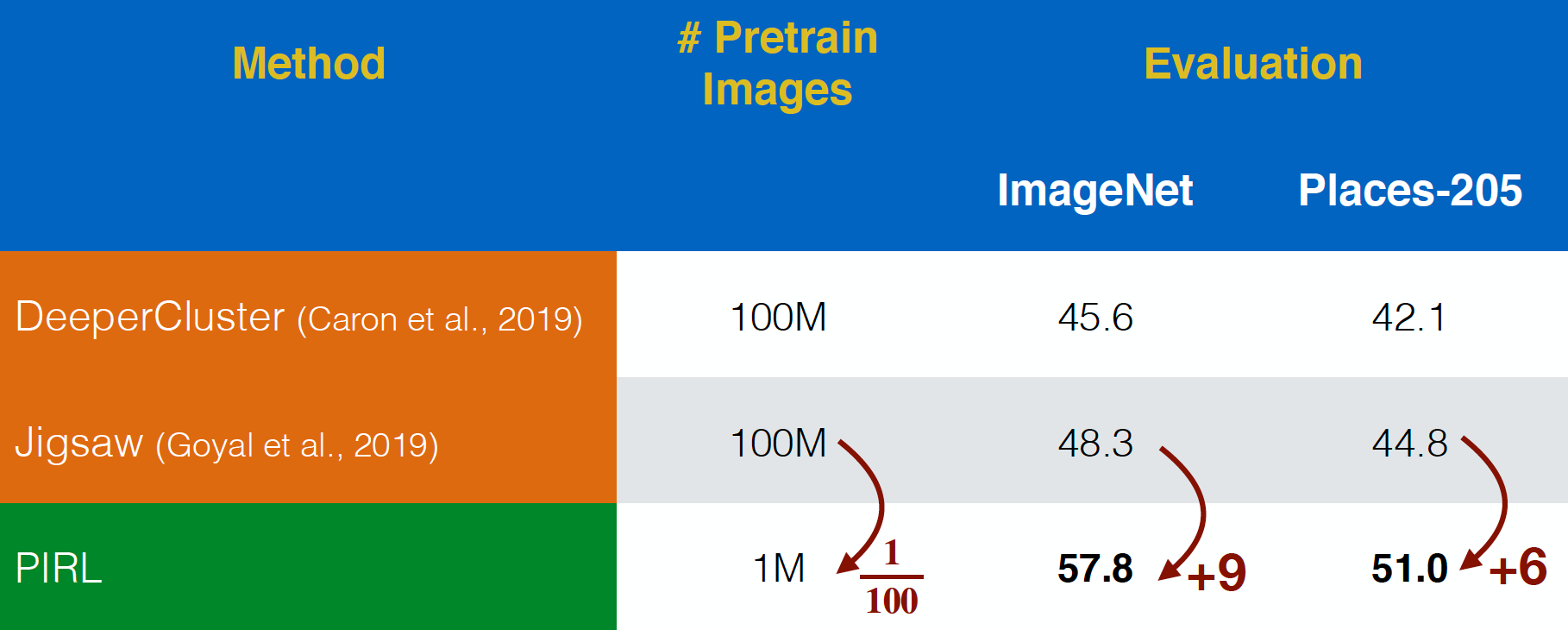
Fig. 20: pre-addestramento su immagini YFCC non modificate.

Caratteristiche semantiche

Ritornando a verificare le caratteristiche semantiche, diamo un’occhiata all’accuratezza del PIRL e del Puzzle per diversi livelli della rappresentazione, da conv1 a res5. È interessante notare che l’accuratezza continua a migliorare per i diversi strati, sia per PIRL che per il Puzzle, ma, nel caso di quest’ultimo, peggiora nel quinto strato.

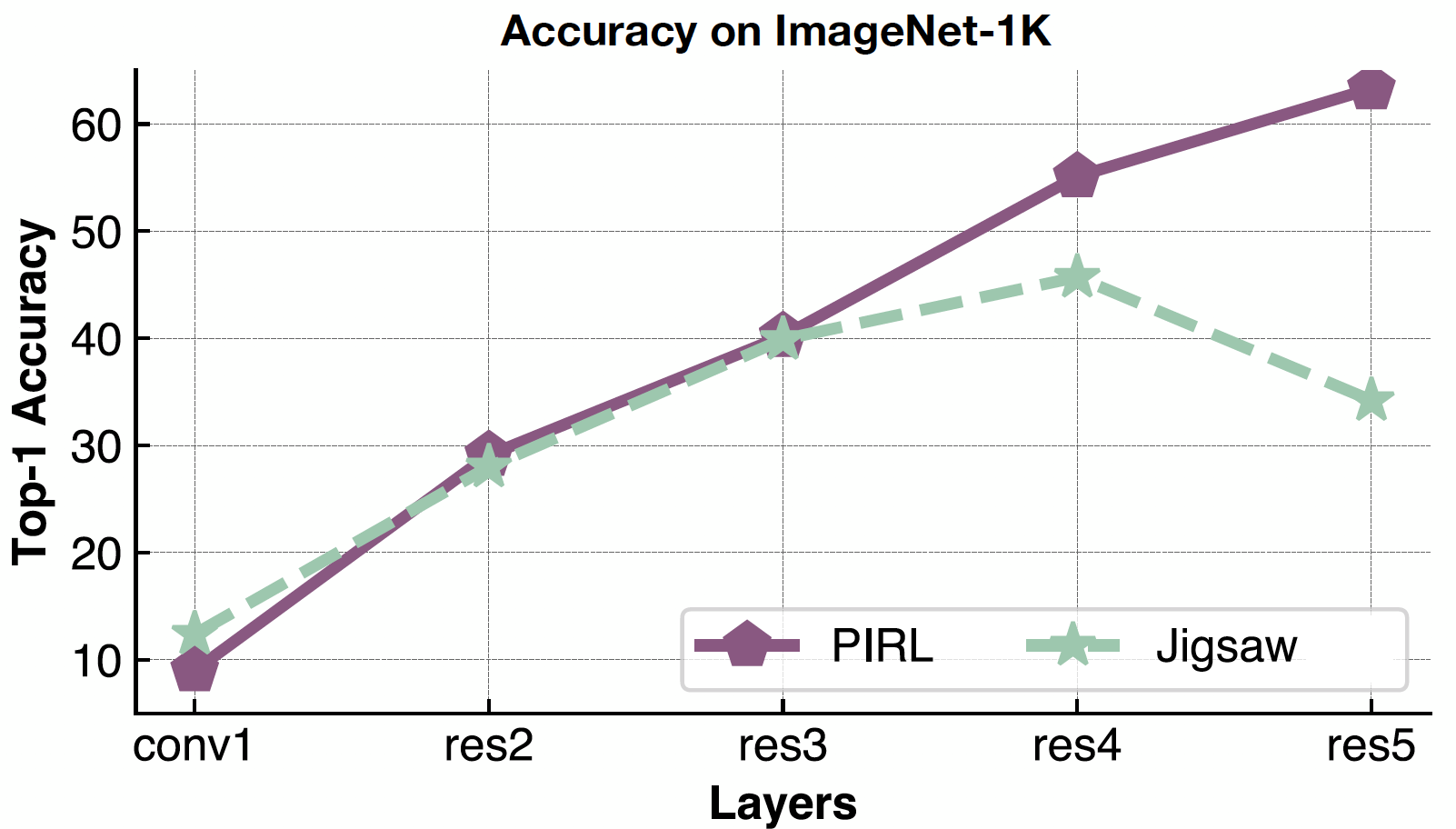
Fig. 21: qualità della rappresentazione di PIRL, strato per strato

Scalabilità

PIRL si comporta molto bene in relazione alla complessità del problema in quanto non si predice mai il numero di permutazioni, ma si utilizza quest’ultimo come input. Di conseguenza, PIRL può facilmente scalare su tutte le $362.880$ possibili permutazioni applicabili alle $9$ finestre, laddove, nel Puzzle, siccome si vogliono prevedere tali permutazioni, si è limitati dalla dimensione dello spazio di output.

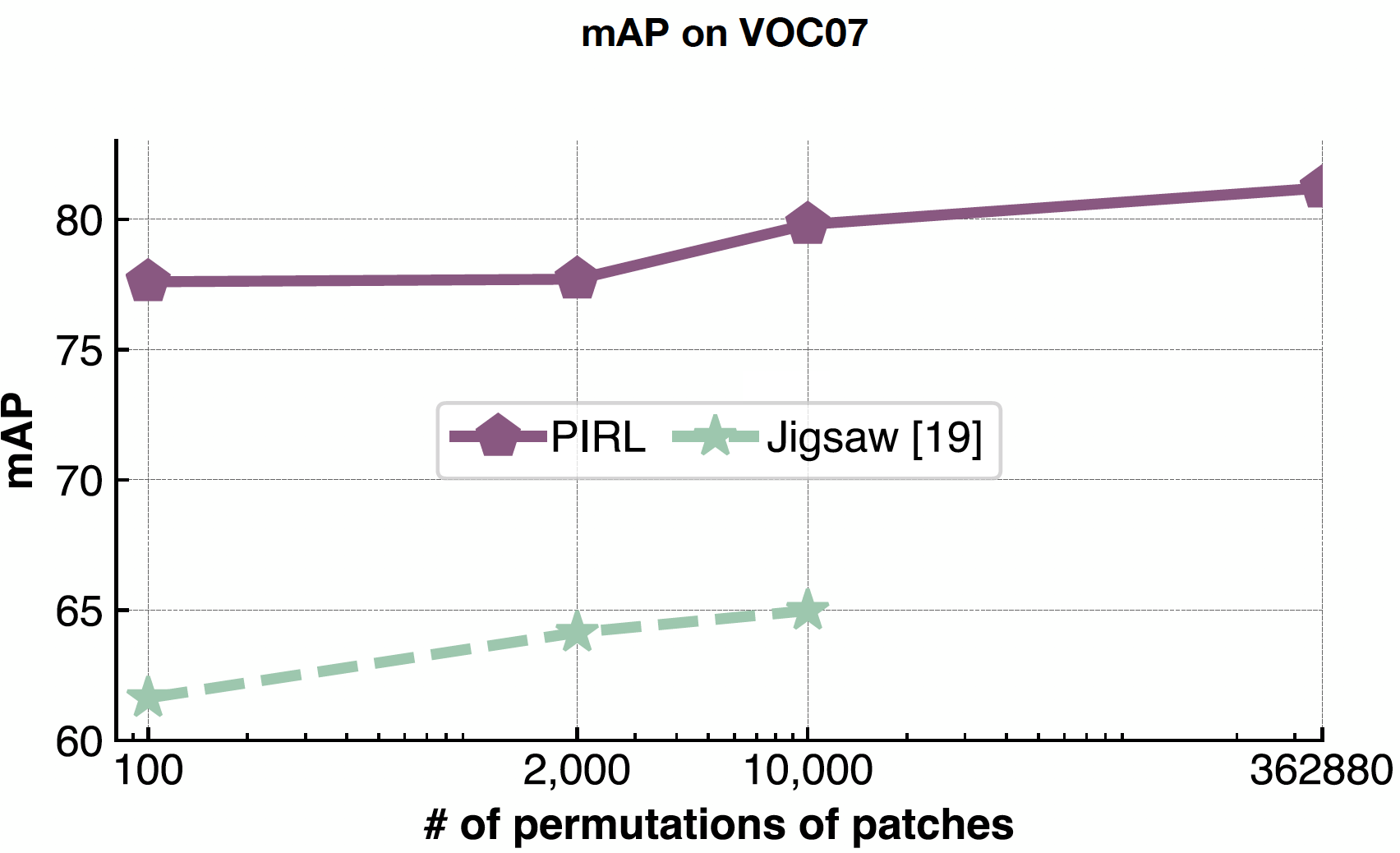
Fig. 22: conseguenza della variazione nel numero di permutazioni delle finestre (*patches*)

Il paper Misra & van der Maaten, 2019, PIRL, mostra inoltre come PIRL potrebbe essere facilmente esteso ad altri compiti come il Puzzle, le rotazioni e via dicendo. In più, potrebbe persino essere esteso a combinazioni di questi compiti, come Puzzle + Rotazioni.

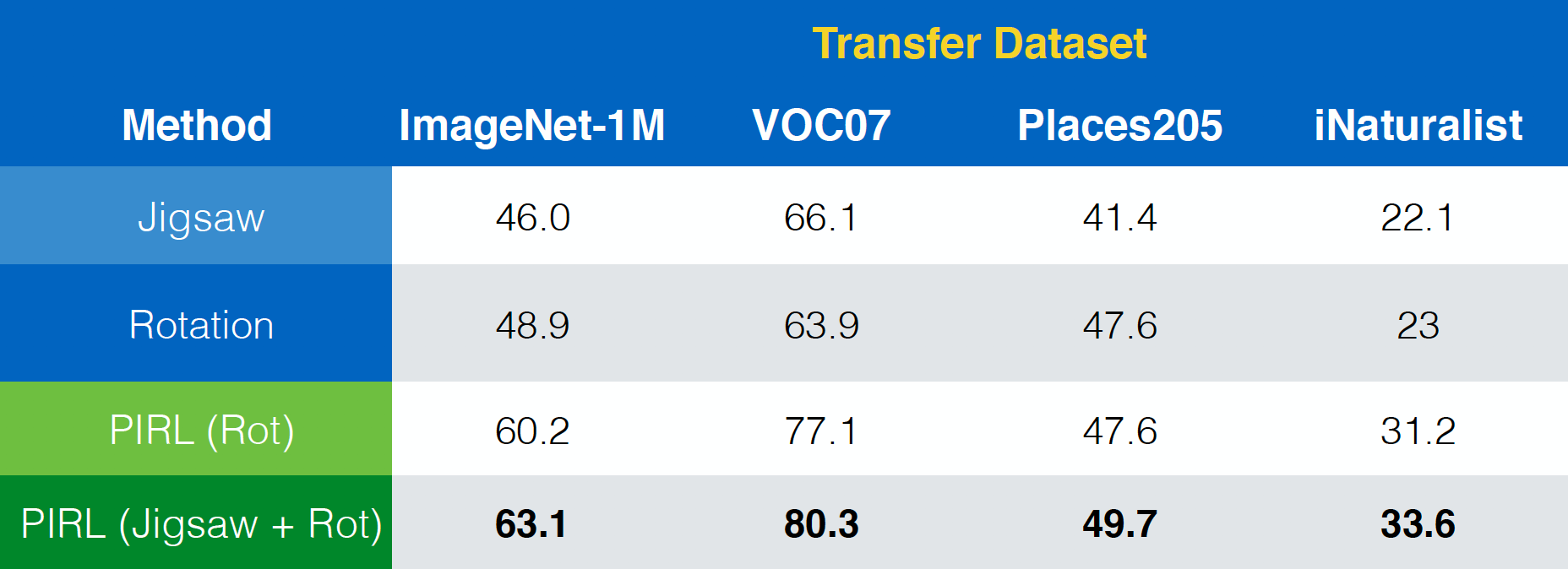
Fig. 23: utilizzo di PIRL con (combinazioni di) diversi compiti di pretesto

Invarianza vs performance

Considerando le proprietà d’invarianza, si potrebbe, in linea di massima, dire che l’invarianza di PIRL sia maggiore rispetto a quella del Clustering, la cui invarianza è, a sua volta, maggiore rispetto ai compiti di pretesto. Analogamente, la performance di PIRL è maggiore di quella del Clustering, la cui performance è maggiore rispetto ai compiti di pretesto. Ciò suggerisce che considerare più invarianze potrebbe migliorare le performance.

Limitazioni

1. Non è molto chiaro per quale insieme dei dati siano importanti le trasformazioni. Il Puzzle funziona, ma non è molto chiaro perché.
2. Vi è un effetto di saturazione all’aumentare della dimensione del modello o dei dati.
3. Quali invarianze sono importanti? (Si potrebbe pensare, come lavoro futuro, a quali invarianze funzionino per uno specifico compito supervisionato.)

In generale, bisognerebbe provare a predire sempre più informazione, provando al contempo ad essere più invarianti possibili.

Chiarimenti importanti

Apprendimento contrastivo e normalizzazione del batch

1. Se si utilizza lo strato di normalizzazione del batch nell’apprendimento contrastivo, le rete non impara solamente una maniera banale di separare i positivi dai negativi (siccome l’informazione passa da un campione al successivo)?

Risposta: In PIRL non è mai stato osservato un fenomeno di questo tipo, cosicché è stata utilizzata la normalizzazione del batch classica.

1. È corretto quindi utilizzare la normalizzazione del batch in ogni rete contrastiva?

Risposta: In generale, sì. In SimCLR si utilizza una variante della classica normalizzazione del batch per emulare grandi dimensioni del batch. Si potrebbe quindi pensare a qualche modifica per rendere l’addestramento più facile.

1. La normalizzazione del batch funziona nel paper di PIRL solamente perché è implementata come banco di memoria, visto che tutte le rappresentazioni non vengono considerate contemporaneamente? (Visto che la normalizzazione del batch non è specificamente utilizzata nel paper di MoCo, per esempio).

Risposta: Sì, in PIRL, lo stesso batch non contiene tutte le rappresentazioni e questo potrebbe spiegare perché funziona qui e non in altri compiti dove le rappresentazioni sono tutte correlate all’interno del batch.

1. Ci sono altre idee su come costruire altre funzioni di perdita calcolate su coppie di dati? Si deve forse utilizzare AlexNet o altre architetture che non hanno la normalizzazione del batch? Oppure c’è un modo di disattivare lo strato di normalizzazione del batch?

Risposta: Generalmente i frame dei video sono correlati fra loro e la performance della normalizzazione del batch degrada quando vi sono autocorrelazioni. Inoltre, anche la più semplice implementazione di AlexNet utilizza la normalizzazione del batch, in quanto rende l’addestramento molto più stabile. Si potrebbe persino usare un livello di apprendimento maggiore e anche per altri compiti downstream. Si potrebbero utilizzare varianti della normalizzazione del batch, come ad esempio normalizzazione di gruppo per compiti di apprendimento video, poiché non dipendono dalla dimensione del batch.

Funzioni di perdita di PIRL

In PIRL, per quale motivo si utilizza NCE (Stimatore Contrastivo del Rumore, Noise Contrastive Estimator) per minimizzare la perdita e non solamente la probabilità negativa della distribuzione dei dati: $h(v_{I},v_{I^{t}})$?

Risposta: Sinceramente, si potrebbero usare entrambi. Il motivo dell’utilizzo di NCE ha più a che fare col modo in cui il paper sul banco di memoria è stato configurato. Così, considerando $k+1$ negativi, si risolvono $k+1$ problemi binari. Si può anche farlo utilizzando un softmax, ovvero si applica il softmax e si minimizza la log-verosimiglianza negativa.

Self-supervised learning project related tips

Come si può far funzionare un semplice modello di apprendimento auto-supervisionato? Come si può iniziare con l’implementazione?

Risposta: Ci sono delle classi di tecniche che sono utili per i compiti iniziali. Ad esempio, si potrebbe partire dai compiti di pretesto. La Rotazione è un compito semplice da implementare. Il numero di pezzi che si muovono è in generale un buon indicatore. Se si pianifica d’implementare un metodo esistente, bisogna guardare più attentamente i dettagli menzionati dall’autore, come l’esatto livello di apprendimento utilizato, il modo in cui le normalizzazioni del batch sono utilizzate, ecc. Più numerosi sono questi dettagli, più ardua è l’implementazione. La prossima cosa critica da considerare è l’aumento dei dati. Se qualcosa funziona, si continua incrementando l’aumento dei dati.

Modelli generativi

Hai mai pensato di combinare modelli generativi con reti contrastive?

Risposta: Generalmente, è una buona idea. Ma non è ancora stata implementata parzialmente perché è problematico e per niente banale addestrare questi modelli. Approcci integrativi sono più difficili da implementare, ma questa potrebbe essere una strada per il futuro.

Distillazione

L’incertezza del modello non dovrebbe incrementare quando viene addestrata con delle etichette più “ricche” fornite da distribuzioni più “soffuse”?

Risposta: Se si addestra il modello su annotazioni con codifiche one-hot, il modello tende ad essere troppo confidente. Alcuni metodi utilizzano tecniche come ammorbidimento delle annotazioni, che è una versione semplificata della distillazione in cui si prova a predire un vettore con codifica one-hot. Ora, anziché predire l’intero vettore, vi si estrae una massa di probabilità: anziché predire un uno e degli zeri, si predice ad esempio un $0,97$ e si aggiunge, ad esempio, $0,01$, $0,01$ e $0,01$ sulle altre componenti (in maniera uniforme). La distillazione è una maniera consapevole di fare ciò. Anziché aumentare casualmente le probabilità di un compito non correlato, si ha una rete pre-addestrata per fare ciò. Generalmente, distribuzioni più soffuse sono molto utili nei metodi di pre-addestramento. I modelli tendono ad essere troppo confidenti e le distribuzioni più soffuse sono più facili da addestrare e convergono più rapidamente. Questi benefici sono presenti nella distillazione.