Reti avversarie generative

Introduzione alle reti generative avversarie (Generative Adversarial Networks, GAN)

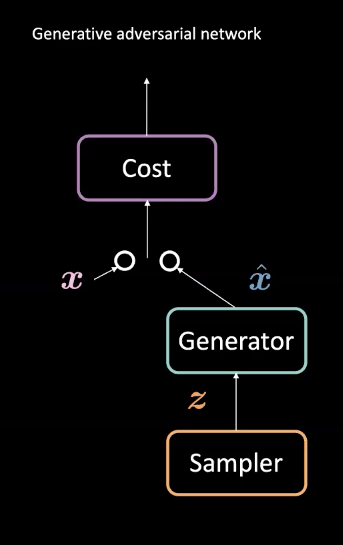
Fig. 1: architettura di una GAN

Le GAN sono un tipo di rete neurale usato per l’apprendimento automatico non supervisionato. Sono composte da due moduli avversari: una rete generatrice (anche chiamata generatore) e una rete del costo. Questi moduli competono fra di loro in maniera tale che la rete del costo cerchi di filtrare istanze fittizie dei dati, mentre il generatore si occupi di ingannare questo filtro tramite la creazione di esempi realistici $\vect{\hat{x}}$. Grazie a questa competizione, il modello impara un generatore che crei dati realistici. Questi possono essere utilizzati in compiti come previsioni future o nella generazione di immagini dopo che la rete sia stata addestrata su un dataset specifico.

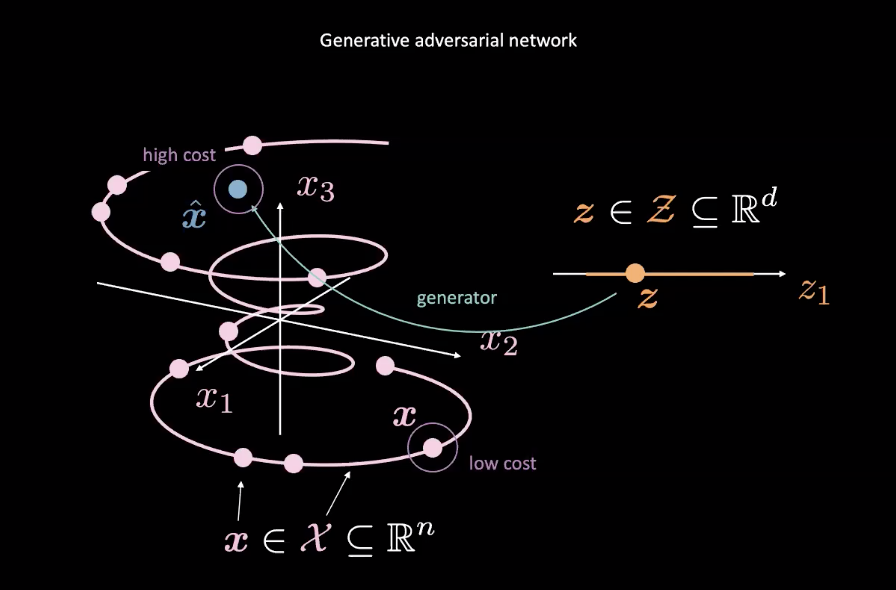
Fig. 2: mappatura di una GAN da una variabile aleatoria

Le GAN sono un esempio di modello ad energia (Energy Based Model, EBM). In quanto tale, la rete di costo è addestrata al fine di assegnare un costo basso per input vicini alla distribuzione reale dei dati, denotata in Fig. 2 dall’espressione $\vect{x}$ in rosa. I dati provenienti da altre distribuzioni, come il $\vect{x}$ in blu (sempre in Fig. 2), dovrebbero avere un costo più elevato. Una perdita basata sull’errore quadratico medio (Mean Square Error, MSE) viene tipicamente utilizzata per calcolare il costo della performance della rete. Vale la pena notare che la funzione di costo produce uno scalare positivo in un intervallo denso specifico (ad esempio, $\text{cost} : \mathbb{R}^n \rightarrow \mathbb{R}^+ \cup {0}$). Questo al contrario di un discriminatore classico il quale classifica sulla base di un insieme discreto.

Nel frattempo, la rete generatrice ($\text{generator} : \mathcal{Z} \rightarrow \mathbb{R}^n$) è addestrata a migliorare la sua mappatura di una variabile aleatoria $\vect{z}$ verso dati realistici $\vect{\hat{x}}$ generati per ingannare la rete del costo. Il generatore viene addestrato nei confronti dell’output della rete di costo, in un tentativo di minimizzazione dell’energia di $\vect{\hat{x}}$. Denotiamo questa energia con $C(G(\vect{z}))$, dove $C(\cdot)$ è la rete di costo è $G(\cdot)$ è la rete generatrice.

L’addestramento della rete di costo si basa sulla minimizzazione della perdita MSE, mentre l’addestramento del generatore avviene attraverso la minimizzazione della rete di costo, usando i gradienti di $C(\vect{\hat{x}})$ su $\vect{\hat{x}}$.

Per assicurare che ai punti esterni alla varietà dei dati venga assegnato un costo alto, mentre ai punti interni risulti un costo basso, la funzione di perdita della rete di costo $\mathcal{L}_{C}$ è $C(x)+[m-C(G(\vect{z}))]^+$ dato un margine positivo $m$. La minimizzazione di $\mathcal{L}_{C}$ richiede sia che $C(\vect{x}) \rightarrow 0$ che $C(G(\vect{z})) \rightarrow m$. La perdita del generatore $\mathcal{L}_{G}$ è semplicemente $C(G(\vect{z}))$, il che incoraggia il generatore ad assicurare che $C(G(\vect{z})) \rightarrow 0$. Tuttavia, questo crea della instabilità in quanto $0 \leftarrow C(G(\vect{z})) \rightarrow m$.

Differenze fra GAN e VAE –>

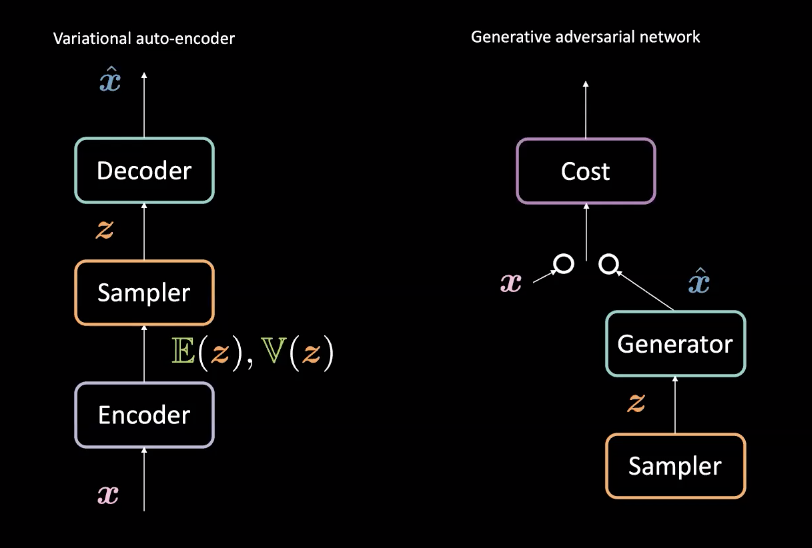
Fig. 3: VAE (a sinistra) vs. GAN (a destra) --- progettazione architettonica

Se comparate con gli Autoencoder variazionali (VAE) di cui alla Settimana 8, le GAN creano dei generatori in maniera leggermente diversa. Si ricordi che i VAE mappano gli input $\vect{x}$ in uno spazio latente $\mathcal{Z}$ tramite un codificatore e, tramite un decodificatore, mappano da $\mathcal{Z}$ di nuovo nello spazio dei dati a produrre $\vect{\hat{x}}$. Si avvalgono della perdita di ricostruzione per fare in modo tale che $\vect{x}$ e $\vect{\hat{x}}$ siano simili. Le GAN, invece, vengono addestrate in un contesto avversario dove le reti generatrice e di costo competono come prima descritto. Queste reti sono addestrate con successo tramite la retropropagazione e i metodi basati sul gradiente. Un paragone fra le differenze architettoniche di questi modelli è presente in Fig. 3.

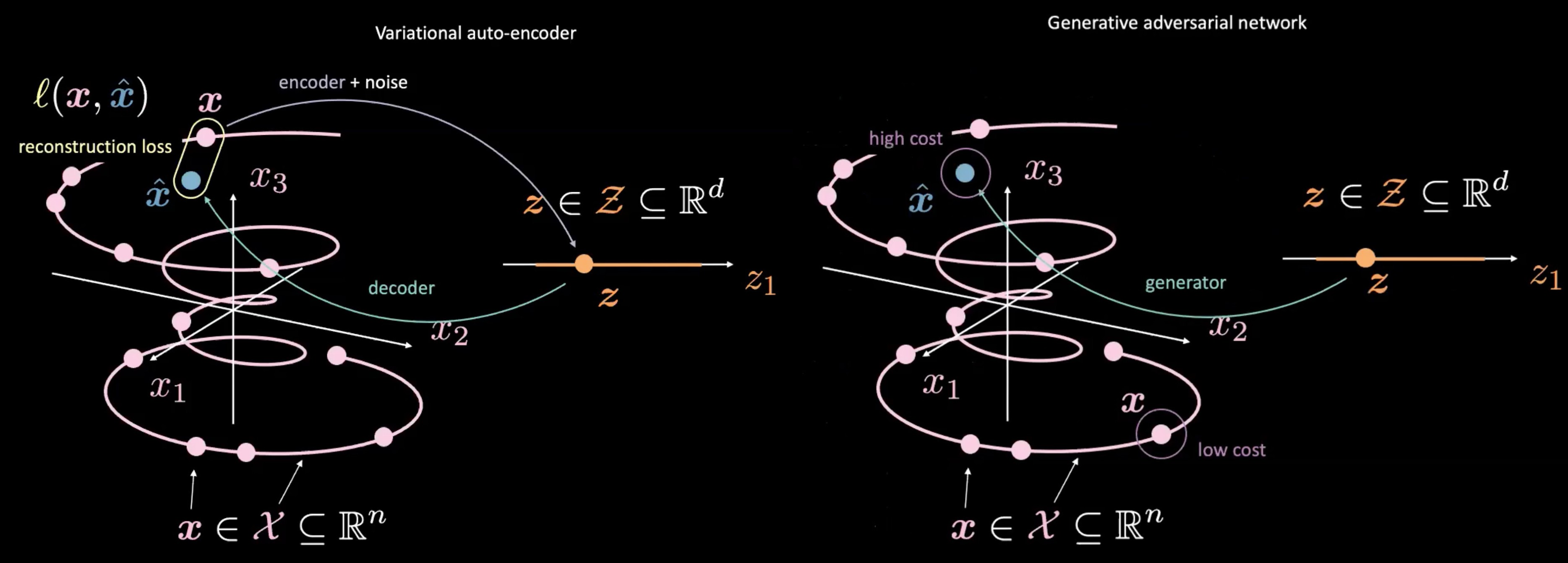
Fig. 4: VAE (a sinistra) vs. GAN (a destra) --- mappatura a partire da un campione casuale $\vect{z}$

Le GAN differiscono dai VAE anche nel modo in cui producono e utilizzano $\vect{z}$. Le GAN iniziano campionando $\vect{z}$, similarmente a quanto succede nello spazio latente di un VAE; utilizzano quindi una rete generativa per mappare $\vect{z}$ in $\vect{\hat{x}}$. Questo $\vect{\hat{x}}$ è quindi passato attraverso una rete discriminatrice/di costo per valutare quanto esso sia “reale”. Una delle principali differenze rispetto ai VAE è che non è necessario misurare una relazione diretta (come la perdita di ricostruzione) fra l’output della rete generativa $\vect{\hat{x}}$ e il dato reale $\vect{x}$. Invece, forziamo $\vect{\hat{x}}$ a essere simile a $\vect{x}$ addestrando un generatore a produrre $\vect{\hat{x}}$ in modo tale che la rete discriminatrice/di costo produca dei punteggi che sono simili a quelli dei dati reali $\vect{x}$ o dei dati “più reali”.

Grosse limitazioni delle GAN

Le GAN possono essere degli strumenti potenti per costruire dei generatori; tuttavia, hanno una serie di grosse limitazioni.

1. Convergenza instabile

Al miglioramento delle performance del generatore nel corso dell’addestramento, segue un degradamento di quelle del discriminatore in quanto quest’ultimo non riesce più a distinguere facilmente fra i dati reali e quelli sintetici. Se il generatore è perfetto, allora le varietà dei dati reali e di quelli sintetici si sovrappongono, con la conseguenza che il discriminatore compirà molte errate classificazioni.

Questo pone un problema per la convergenza della GAN: il feedback ricevuto dal discriminatore diviene sempre meno significativo nel tempo. Se la GAN continua l’addestramento oltre al punto in cui il discriminatore inizia a dare feedback completamente casuali, allora il generatore inizia ad addestrarsi su riferimenti completamente inaffidabili e la sua qualità potrebbe degradarsi. [Fare riferimento a convergenza dell’addestramento nelle GAN]

Il risultato di questa natura avversaria fra il generatore e il discriminatore è un punto di equilibrio instabile piuttosto che un vero e proprio equilibrio.

2. Scomparsa del gradiente (o “gradiente evanescente”)

Proviamo a utilizzare la entropia binaria incrociata come perdita di una GAN

Come il discriminatore diventa più “fiducioso”, $D(\vect{x})$ si avvicina a $1$ e $D(\vect{\hat{x}})$ a $0$. Questa “fiducia” nella previsione fa sì che gli output della rete di costo vengano “spostati” verso regioni piatte dove il gradiente diviene più saturato. Queste regioni forniscono gradienti piccoli ed evanescenti che danneggiano l’addestramento della rete generatrice. Dunque, quando si addestra una GAN, ci si vuole assicurare che il costo aumenti gradualmente con il livello di certezza.

3. Collasso della moda

Se un generatore mappa tutti i $\vect{z}$ del campionatore ad un unico $\vect{\hat{x}}$ in grado d’imbrogliare il discriminatore, allora il generatore produrrà solamente questo $\vect{\hat{x}}$. Alla fine, il discriminatore imparerà a distinguere specificamente questo input sintetico. Il risultato di ciò è che il generatore semplicemente scopre il $\vect{\hat{x}}$ più plausibile e il ciclo continua; conseguentemente, il discriminatore rimane intrappolato in minimi locali mentre passa in rassegna sempre gli stessi $\vect{\hat{x}}$ sintetici. Una possibile soluzione a questa problematica è l’applicazione di una qualche penalità al generatore così da sfavorire la produzione ripetuta dello stesso output dati input differenti fra di loro.

Codice sorgente di una rete avversaria generativa profonda convoluzionale (Deep Convolutional Generative Adversarial Network, DCGAN)

Il codice sorgente dell’esempio è reperibile qui.

Il generatore

1. Il generatore esegue un sovracampionamento dell’input utilizzando vari moduli nn.ConvTranspose2d inframmezzati da nn.BatchNorm2d e nn.ReLU.
2. Al termine della parte sequenziale, la rete utilizza nn.Tanh() per confinare l’output nell’intervallo $(-1; 1)$.
3. Il vettore aleatorio d’input ha dimensione $nz$. L’output ha una dimensione di $nc \times 64 \times 64$, dove $nc$ è il numero di canali.

class Generator(nn.Module):
    def __init__(self):
        super().__init__()
        self.main = nn.Sequential(
            # l'input è Z, passa attraverso una convoluzione
            nn.ConvTranspose2d(     nz, ngf * 8, 4, 1, 0, bias=False),
            nn.BatchNorm2d(ngf * 8),
            nn.ReLU(True),
            # dimensione dello stato (ngf * 8) x 4 x 4
            nn.ConvTranspose2d(ngf * 8, ngf * 4, 4, 2, 1, bias=False),
            nn.BatchNorm2d(ngf * 4),
            nn.ReLU(True),
            # dimensione dello stato (ngf * 8) x 8 x 8
            nn.ConvTranspose2d(ngf * 4, ngf * 2, 4, 2, 1, bias=False),
            nn.BatchNorm2d(ngf * 2),
            nn.ReLU(True),
            # dimensione dello stato (ngf * 2) x 16 x 16
            nn.ConvTranspose2d(ngf * 2,     ngf, 4, 2, 1, bias=False),
            nn.BatchNorm2d(ngf),
            nn.ReLU(True),
            # dimensione dello stato (ngf * 1) x 32 x 32
            nn.ConvTranspose2d(    ngf,      nc, 4, 2, 1, bias=False),
            nn.Tanh()
            # dimensione dello stato (nc) x 64 x 64
        )

    def forward(self, input):
        output = self.main(input)
        return output

Il discriminatore

1. È importante utilizzare nn.LeakyReLU come funzione di attivazione onde evitare l’azzeramento del gradiente nelle regioni negative. Senza questi gradienti, il generatore non riceverebbe aggiornamenti.
2. Alla fine della parte sequenziale, il discriminatore utilizza nn.Sigmoid() per classificare l’input.

class Discriminator(nn.Module):
    def __init__(self):
        super().__init__()
        self.main = nn.Sequential(
            # l'input è (nc) x 64 x 64
            nn.Conv2d(nc, ndf, 4, 2, 1, bias=False),
            nn.LeakyReLU(0.2, inplace=True),
            # dimensione dello stato (ndf) x 32 x 32
            nn.Conv2d(ndf, ndf * 2, 4, 2, 1, bias=False),
            nn.BatchNorm2d(ndf * 2),
            nn.LeakyReLU(0.2, inplace=True),
            # dimensione dello stato (ndf*2) x 16 x 16
            nn.Conv2d(ndf * 2, ndf * 4, 4, 2, 1, bias=False),
            nn.BatchNorm2d(ndf * 4),
            nn.LeakyReLU(0.2, inplace=True),
            # dimensione dello stato (ndf*4) x 8 x 8
            nn.Conv2d(ndf * 4, ndf * 8, 4, 2, 1, bias=False),
            nn.BatchNorm2d(ndf * 8),
            nn.LeakyReLU(0.2, inplace=True),
            # dimensione dello stato (ndf*8) x 4 x 4
            nn.Conv2d(ndf * 8, 1, 4, 1, 0, bias=False),
            nn.Sigmoid()
        )

    def forward(self, input):
        output = self.main(input)
        return output.view(-1, 1).squeeze(1)

Queste due classi sono inizializzate con i nomi di netG e netD.

Funzione di perdita per la GAN

Utilizziamo l’entropia incrociata binaria (Binary Cross Entropy, BCE) fra l’obiettivo e l’output.

criterion = nn.BCELoss()

Preparazione

Predisponiamo un rumore fisso fixed_noise di dimensione opt.batchSize e della lunghezza del vettore aleatorio nz. Inoltre, creiamo delle etichette per i dati reali e quelli generati (sintetici): rispettivamente real_label e fake_label.

fixed_noise = torch.randn(opt.batchSize, nz, 1, 1, device=device)
real_label = 1
fake_label = 0

Dopodiché predisponiamo gli ottimizzatori per la rete discriminatrice e generatrice.

optimizerD = optim.Adam(netD.parameters(), lr=opt.lr, betas=(opt.beta1, 0.999))
optimizerG = optim.Adam(netG.parameters(), lr=opt.lr, betas=(opt.beta1, 0.999))

Addestramento

Ogni epoca di addestramento è suddivisa in due passi.

Il primo passo consiste nell’aggiornamento della rete discriminatrice. Innanzitutto, le diamo come input i dati reali provenienti dai dataloaders, calcoliamo la perdita fra l’output e la real_label e accumuliamo i gradienti via retropropagazione. Dopodiché, passiamo al discriminatore i dati sintetici prodotti dal generatore utilizzando il fixed_noise, calcoliamo la perdita fra l’output e la fake_label e accumuliamo il gradiente. Infine, utilizziamo i gradienti accumulati per calcolare i parametri della rete discriminatrice.

Si noti che effettuiamo un detach (“distaccamento”) dei dati fittizi per impedire la propagazione del gradiente al generatore mentre stiamo addestrando il discriminatore.

Inoltre, si noti che dobbiamo chiamare zero_grad() solamente una volta all’inizio per azzerare i gradienti in modo tale che i gradienti provenienti sia dai dati reali che da quelli sintetici possano essere utilizzati per l’aggiornamento. Le due chiamate .backward() accumulano detti gradienti. Infine, necessitiamo solo di una chiamata optimizerD.step() per aggiornare i parametri.

# addestramento con dati reali (real)
netD.zero_grad()
real_cpu = data[0].to(device)
batch_size = real_cpu.size(0)
label = torch.full((batch_size,), real_label, device=device)

output = netD(real_cpu)
errD_real = criterion(output, label)
errD_real.backward()
D_x = output.mean().item()

# addestramento con dati sintetici (fake)
noise = torch.randn(batch_size, nz, 1, 1, device=device)
fake = netG(noise)
label.fill_(fake_label)
output = netD(fake.detach())
errD_fake = criterion(output, label)
errD_fake.backward()
D_G_z1 = output.mean().item()
errD = errD_real + errD_fake
optimizerD.step()

Il secondo passo consiste nell’aggiornare la rete generatrice. Stavolta, diamo al discriminatore i dati fittizi, ma computiamo la perdita con la real_label! Lo scopo di ciò è addestrare il generatore a produrre $\vect{\hat{x}}$ realistici.

netG.zero_grad()
label.fill_(real_label)  # le fake_labels sono reali per la fz. di costo del generatore
output = netD(fake)
errG = criterion(output, label)
errG.backward()
D_G_z2 = output.mean().item()
optimizerG.step()