World Model e reti avversarie generative

Modelli della realtà (world model) per il controllo autonomo

Uno degli utilizzi più importanti dell’apprendimento auto-supervisionato è imparare modelli della realtà (world model, letteralmente “modello del mondo”) per il controllo. Quando noi umani svolgiam un compito, facciamo riferimento a un modello interiore sul funzionamento del mondo. Per esempio, costruiamo delle intuizioni sulle leggi della fisica da quando abbiamo circa 9 mesi, principalmente tramite l’osservazione. In un certo senso, ciò è simile all’apprendimento auto-supervisionato; apprendendo a predire ciò che accadrà, impariamo princìpi astratti, così come l’apprendimento auto-supervisionato apprende le caratteristiche latenti. Ma, facendo un passo ulteriore, i modelli interni ci permettono di agire sul mondo. Ad esempio, possiamo utilizzare le intuizioni sulla fisica da noi imparate e ciò che abbiamo appreso sul funzionamento dei nostri muscoli per predire — ed eseguire – come prendere al volo una penna che sta cadendo.

Che cos’è un modello della realtà?

Un sistema d’intelligenza autonomo comprende quattro moduli principali (Fig. 1). Innanzitutto, il modulo di percezione (perception) osserva il mondo e ne calcola una rappresentazione del suo stato. Questa rappresentazione è incompleta in quanto 1) l’agente non è in grado di osservare l’universo nella sua interezza e 2) l’accuratezza delle osservazioni è limitata. Vale anche la pena notare che nel modello feed-forward, il modulo di percezione è presente solo nell’istante iniziale. Dopodiché, il modulo attuativo (actor, anche chiamato modulo di politica) immagina di compiere un’azione sulla base dello stato del mondo o di una rappresentazione di quest’ultimo. Come terzo passo, il modulo di modellazione (model) predice il risultato dell’azione dato lo stato del mondo (o una sua rappresentazione) ed eventualmente delle caratteristiche lantenti. Questa previsione viene passata avanti al prossimo istante temporale come stima per il prossimo stato del mondo, assumento il ruolo del modulo di percezione di cui al primo istante temporale. La Fig. 2 fornisce una dimostrazione nel dettaglio di questo processo feed-forward. Infine, il modulo di critica (critic) trasforma questa stessa previsione in un costo dovuto all’attuazione dell’azione proposta: ad esempio, data la velocità con la quale credo la penna stia cadendo, se muovo i muscoli in un determinato modo, di quanto mancherò la presa?

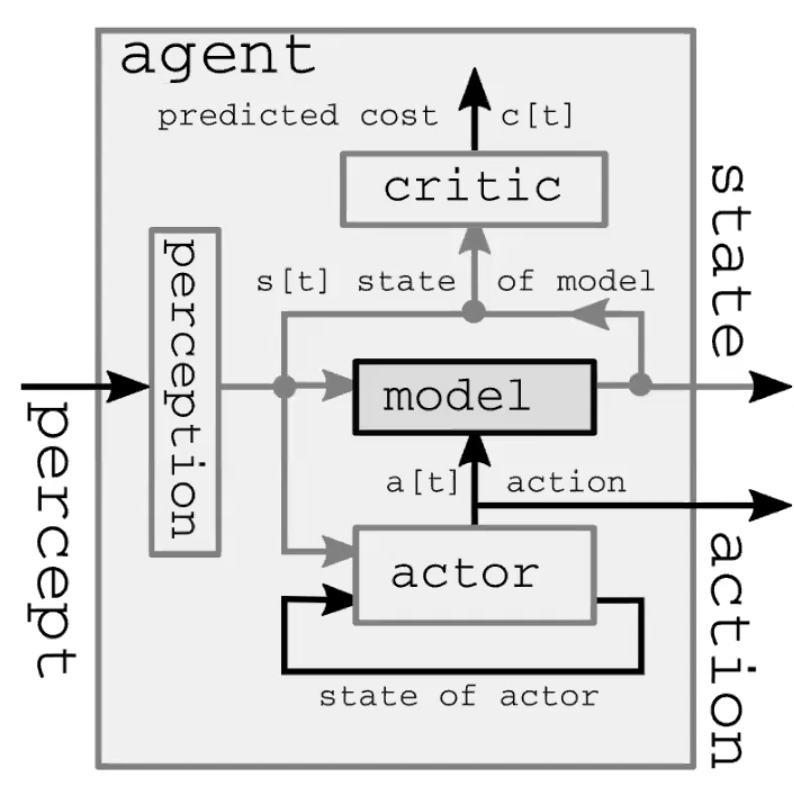
Fig. 1: dimostrazione dell'architettura di un sistema intelligente artificiale di tipo world model.

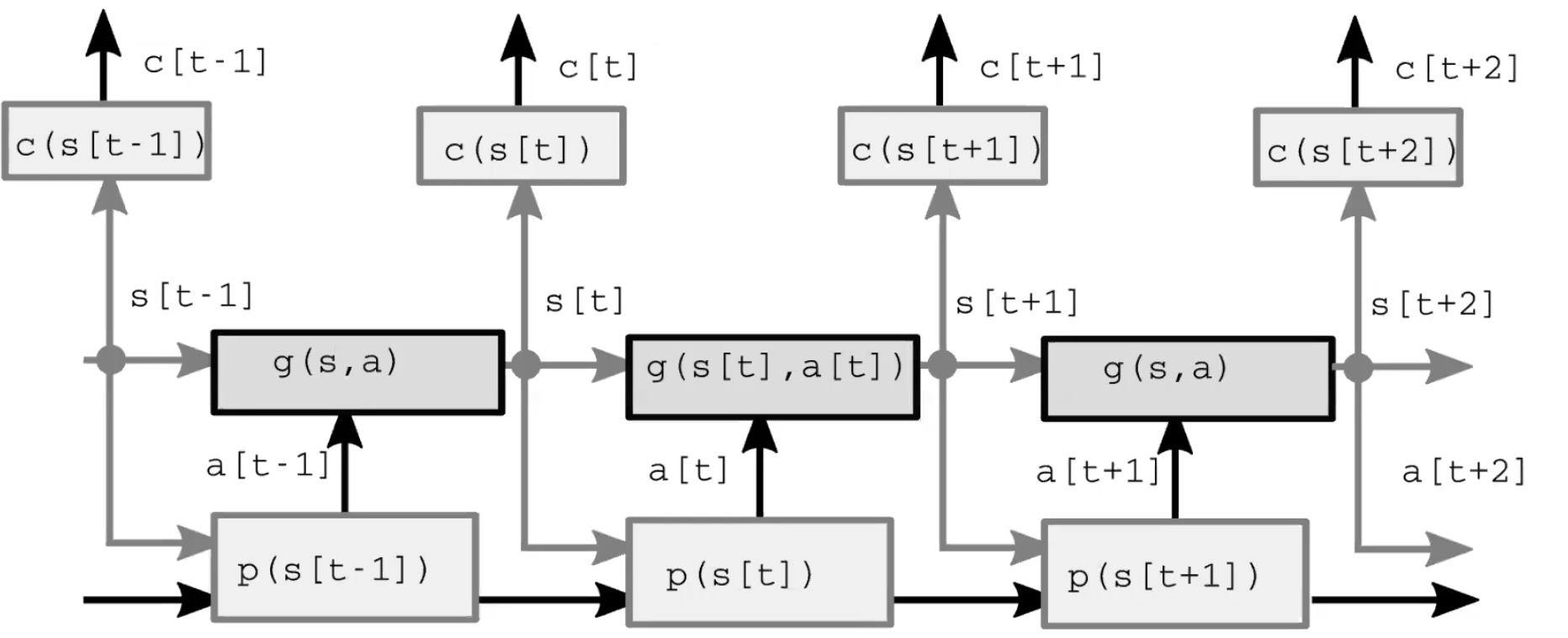
Fig. 2: architettura del modello

La configurazione classica

Nel controllo ottimo classico, non vi è alcun modulo attuativo / di politica, ma vi è solo una variabile attuativa. Questa formulazione è ottimizzata da un metodo classico chiamato Model Predictive Control (“modello di controllo predittivo”), che è stato utilizzato dalla NASA negli anni ‘60 per calcolare le traiettorie del razzo al passaggio da calcolatori umani (principalmente matematiche di colore) ai computer elettronici. Possiamo pensare a questi sistemi come una rete neurale ricorrente (recurrent neural network, RNN) “srotolato” nel tempo, e alle azioni come variabili latenti; possiamo quindi usare la retropropagazione ed i metodi a gradiente (o eventualmente altri metodi, come la programmazione dinamica per un insieme di azioni discrete) per inferire la sequenza di azioni che minimizzi la somma dei costi per ogni istante temporale.

Nota: utilizziamo il termine “inferenza” per le variabili latenti e “apprendimento” per i parametri, nonostante il processo di ottimizzazione sia fra loro generalmente simile. Una differenza importante è che una variabile latente assume un valore specifico per ogni istanza dei dati, mentre i parametri sono condivisi fra le varie istanze.

Una miglioria

Preferiremmo non passare per il processo complicato di attuazione della retropropagazione ogni volta che vogliamo ottenere un piano di previsione. Per risolvere ciò, utilizziamo lo stesso trucchetto già applicato agli autoencoder variazionali per migliorare la codificazione sparsa: addestriamo un autoencoder per predire direttamente, dalla rappresentazione del mondo, la sequenza attuativa ottimale. Sotto questo regime, il codificatore diviene una “rete della politica”.

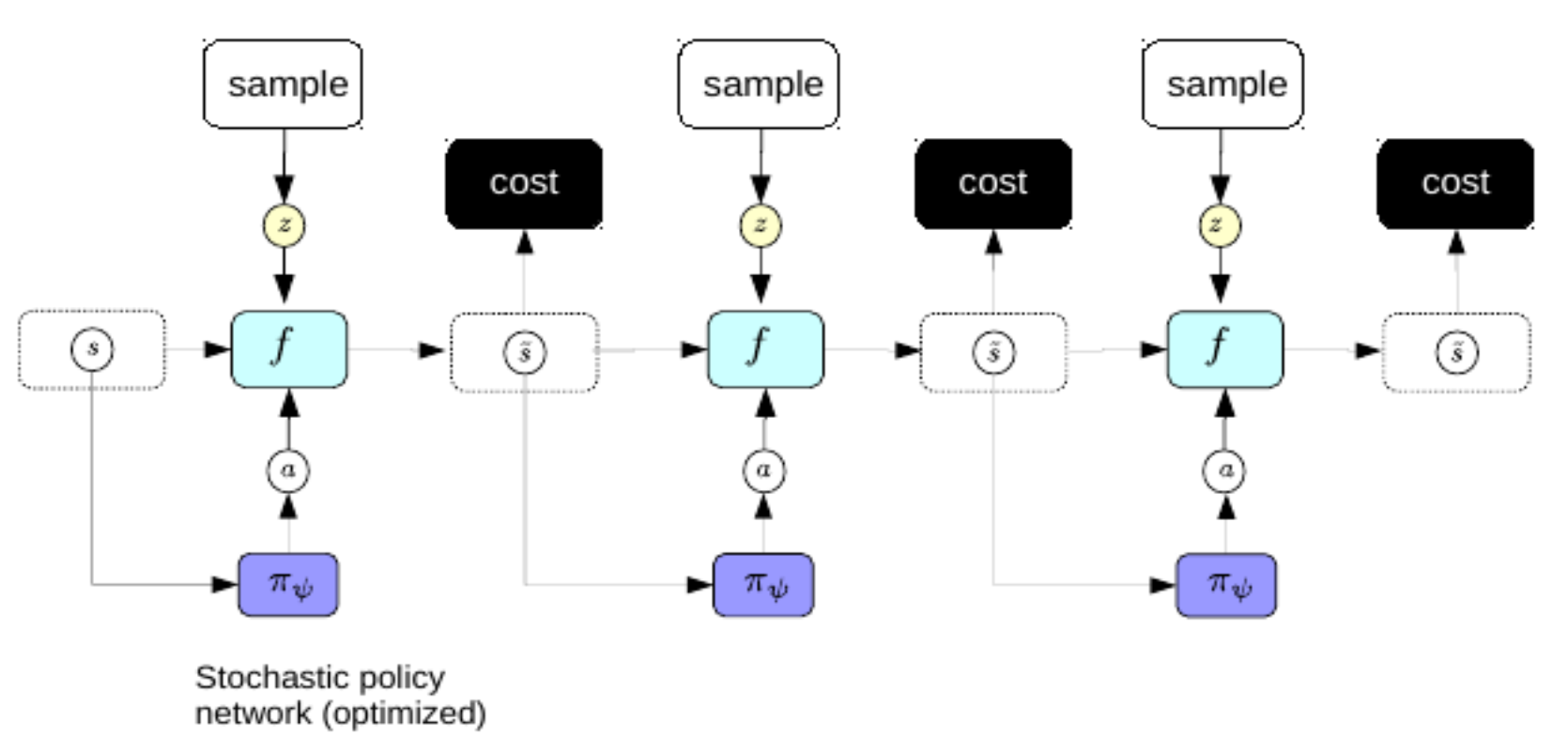
Fig. 3: rete della politica

Una volta addestrata, possiamo usare le reti della politica per predire la sequenza di azioni ottimale immediatamente dopo la percezione.

Apprendimento per riforzo (Reinforcement Learning, RL)

Le principali differenze fra il RL e quanto finora studiato sono duplici:

1. Nel RL, la funzione di costo è una “scatola nera” (black box), ovvero non ci è nota. In altre parole, l’agente non capisce le dinamiche che stanno dietro alla ricompensa.
2. Nella configurazione del RL, non si utilizza un modello “in avanti” (forward) per fare passi nell’ambiente. Invece, si interagisce con il mondo reale e s’impara il risultato delle azioni tramite l’osservazione di ciò che accade di conseguenza a esse. Nel mondo reale, la nostra stima dello stato del mondo è imperfetta, così che non è sempre possibile predire cosa accadrà nel futuro prossimo.

Il problema principale del RL è che la funzione di costo non è differenziabile. Ciò significa che l’unica modalità di apprendimento è tramite tentativi ed errori (trial and error). La questione diviene dunque come esplorare lo spazio degli stati in maniera efficiente. Una volta risolto questo punto, il prossimo problema è il trade-off fondamentale fra l’esplorazione e lo sfruttamento (explore vs. exploit): è preferibile compiere azioni al fine di apprendere in maniera massimale l’ambiente, oppure sfruttare quanto già imparato per ottenere una ricompensa più alta possibile?

I metodi di tipo Actor-Critic (“agente-critico”) sono una famiglia molto diffusa di algoritmi di RL che si propongono di addestrare sia un agente che un critico. Molti metodi di RL funzionano in maniera simile, addestrando un modello della funzione di costo (il critico). Nei metodi Actor-Critic il ruolo del critico è di apprendere il valore atteso della funzione del valore. Questo permette una retropropagazione attraverso il modulo, poiché il critico è una rete neurale. La responsabilità dell’attore è quella di proporre azioni da compiere nell’ambiente, mentre il lavoro del critico è di apprendere un modello della funzione di costo. L’attore e il critico lavorano in tandem, il che risulta in un apprendimento più efficiente rispetto al modello con solo attore. Se non si dispone di un buon modello della realtà, è molto più difficile apprendere: ad esempio, l’auto sull’orlo del burrone non saprà che cadere giù da quest’ultimo sia una idea cattiva. Il modello della realtà permette agli umani e agli animali d’imparare molto più rapidamente degli agenti di RL: disponiamo già di un modello della realtà veramente buono nella nostra testa.

Non possiamo sempre prevedere il futuro reale a causa di due tipi d’incertezza intrinseca: aleatoria ed epistemica. L’incertezza aleatoria è dovuta da fattori dell’ambiente che non si possono controllare od osservare. L’incertezza epistemica è dovuta ad un’assenza, nel modello, di dati di addestramento, ragion per cui il modello non riesce a prevedere il futuro.

Il modello di tipo forward vorrebbe predire

dove $z$ è una variabile latente di cui non conosciamo il valore. Essa rappresenta ciò che non si può conoscere del mondo, ma che comunque influenza la previsione (ovvero, l’incertezza aleatoria). È possibile regolarizzare $z$ tramite sparsità, rumore o tramite un codificatore. Si può usare il modello forward per imparare a pianificare. Ciò è possibile disponendo di un decodificatore che decodifichi una concatenazione della rappresentazione dello stato e dell’incertezza $z$. La miglior $z$ è quella che minimizza la differenza fra lo stato stimato $\hat s_{t+1}$ e lo stato osservato $s_{t+1}$.

Reti avversarie generative (Generative Adversarial Networks, GAN)

Vi sono numerose variazioni delle GAN: qui vediamo una GAN come una forma di modelli ad energia con metodi contrastivi. Innalza l’energia delle istanze contrastive e la abbassa per le istanze di addestramento. Una GAN base è composta di due parti: un generatore (generator) che produce esempi contrastivi in maniera intelligente e un discriminatore (discriminator, a volte chiamato critico) che essenzialmente è una funzione di costo e agisce come un modello ad energia. Entrambe le parti sono reti neurali.

I due tipi di input della GAN sono rispettivamente le istanze di addestramento e le istanze contrastive. La GAN fa passare le istanze di addestramento attraverso il discriminatore e abbassa l’energia di queste. Per quanto riguarda le istanze contrastive, la GAN campiona le variabili latenti a partire da una data distribuzione, le passa attraverso il generatore, che produce qualcosa di simile agli esempi di addestramento; inifine, le passa attraverso il discriminatore per innalzarne l’energia. La funzione di perdita del discriminatore è la seguente:

dove $L_d$ può essere una funzione di perdita basata su di un margine (fra valore atteso e osservato), come $F(y) + [m - F(\bar{y})]^+$ oppure $\log(1 + \exp[F(y)]) + \log(1 + \exp[-F(\bar{y})])$ fintantoché renda $F(y)$ decrescente e $F(\bar{y})$ crescente. In questo contesto, $y$ è la classe di appartenenza dell’istanza, mentre $\bar{y}$ è la risposta del modello. La funzione di perdita per il generatore invece è la seguente:

dove $z$ è la variabile latente e $G$ è la rete neurale generativa. Vogliamo far sì che il generatore adatti i suoi pesi e produca $\bar{y}$ con un’energia bassa affinché possa “sbugiardare” il discriminatore.

Il motivo per cui questo tipo di modello è chiamato “rete avversaria generativa” è perché abbiamo due funzioni obiettivo che sono incompatibili fra di loro e dobbiamo minimizzarle contemporaneamente. Non è un problema di discesa del gradiente, in quanto l’obiettivo è trovare un equilibrio di Nash fra queste due funzioni: una discesa del gradiente non è in grado di fare ciò da sé.

Sorgeranno dei problemi quando avremo istanze che saranno vicine alla varietà reale dei dati. Immaginiamo di avere una varietà infinitamente sottile. Il discriminatore deve produrre una probabilità pari a $0$ fuori dalla varietà e probabilità infinita al suo interno. Siccome questo è molto difficile da ottenere, la GAN utilizza una sigmoide e produce $0$ fuori dalla varietà e $1$ al suo interno. Il problema con questo tipo di configurazione è che, se addestriamo il sistema con successo, il discriminatore produce $0$ fuori dalla varietà