Autoencoder discriminativi ricorrenti sparsi

Autoencoder discriminativi ricorrenti sparsi (Discriminative recurrent Sparse Auto-Encoder, DrSAE)

L’idea dietro al DrSAE consiste nel combininare la codificazione sparsa, o gli autoencoder sparsi, con l’addestramento discriminativo.

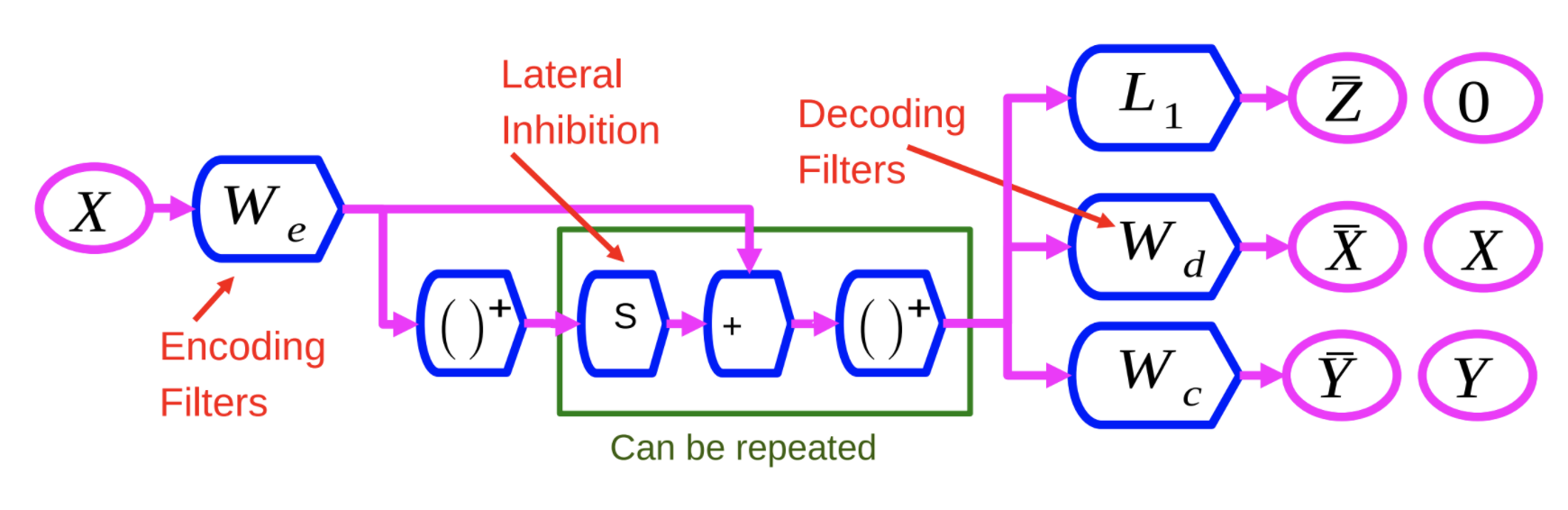
Fig. 1: Autoencoder discriminativi ricorrenti sparsi

Il codificatore, $W_e$ è simile al codificatore del metodo LISTA. La variabile $X$ viene passata attraverso $W_e$ e attraverso delle funzioni non-lineari. Questo risultato è poi moltiplicato per un’altra matrice appresa, $S$, ed aggiunto a $W_e$. Dopodiché viene passato nuovamente attraverso delle funzioni non-lineari. Il processo può venir ripetuto più volte; ogni ripetizione identifica uno strato.

Addestriamo questa rete neurale con tre criteri differenti:

1. $L_1$: applichiamo il criterio $L_1$ al vettore delle caratteristiche $X$ al fine di renderlo sparso.
2. Ricostruzione di $X$: ciò viene svolto utilizzando una matrice di decodificazione che riproduce l’input dato l’output, il che si ottiene minimizzando l’errore quadrato, indicato da $W_d$ nella Fig. 1.
3. Aggiunta di un terzo termine: questo terzo termine, indicato da $W_c$, è un semplice classificatore lineare il quale tenta di predire una categoria.

Il sistema è addestrato al fine di minimizzare contemporaneamente tutti questi 3 criteri.

Il vantaggio di ciò è il seguente: costringendo il sistema a trovare rappresentazioni che possono ricostruire l’input, si sta praticamente distorcendo il sistema all’estrazione di caratteristiche che contengano il massimo dell’informazione riguardo l’input. In altre parole, arricchisce le caratteristiche.

Sparsità di gruppo

Qui l’idea è di generare caratteristiche sparse, ma non normali caratteristiche estraibili tramite convoluzione, ma caratteristiche che siano sparse dopo l’operazione di aggregazione (pooling).

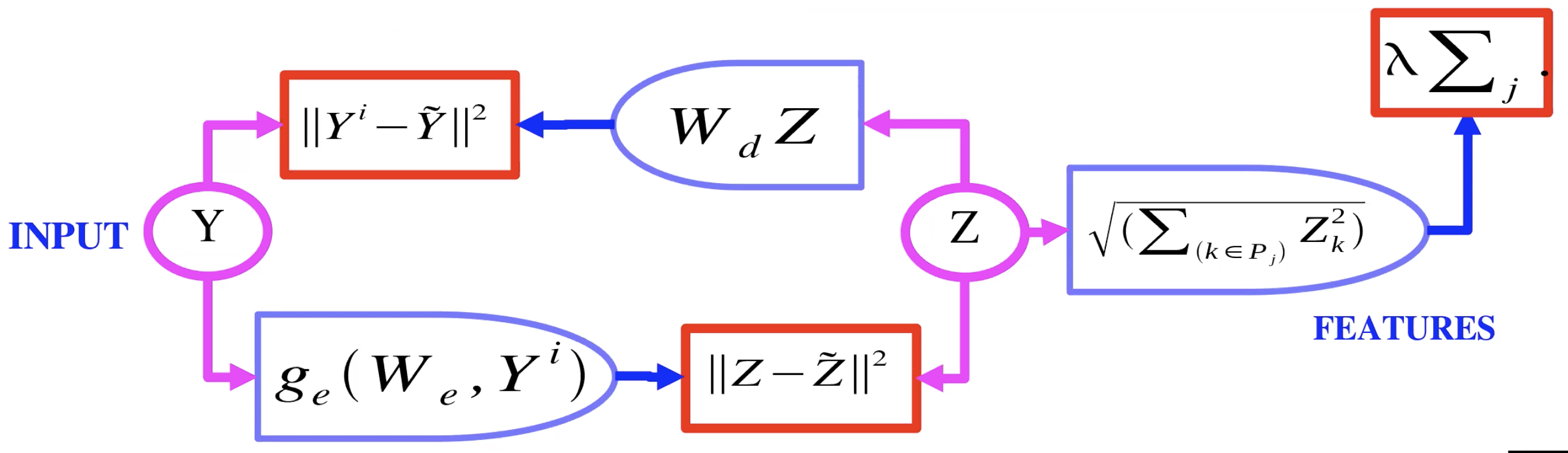
Fig. 2: Autoencoder con sparsità di gruppo

La Fig. 2 mostra un esempio di autoencoder con sparsità di gruppo. Qui, invece di passare la variabile latente $Z$ attraverso un $L_1$, grossomodo passa attraverso un $L_2$ di gruppo. Cioè, si calcola la norma $L_2$ per ogni componente in un gruppo di $Z$, e si prende la somma di queste norme. Così ora che abbiamo ciò che viene utilizzato come regolarizzatore, possiamo ottenere della sparsità all’interno di gruppi di $Z$. Questi gruppi, o insiemi di caratteristiche, tendono a raggruppare assieme caratteristiche che sono reciprocamente simili.

AE con sparsità di gruppo: domande e chiarimenti

Domanda: si può, per i VAE, in maniera simile a quanto fatto precedentemente, utilizzare una strategia del tipo classificatore + regolarizzatore?

Risposta: aggiungere rumore e forzare della sparsità in un VAE sono due strategie per ridurre l’informazione che giunge alla variabile latente / al codice. Prevengono l’apprendimento della funzione identità.

D: Nel capitolo “AE con sparsità di gruppo”, cosa è $P_j$?

R: $p$ è un’aggregazione di caratteristiche. Per un vettore $z$, equivale ad un sottoinsieme dei valori in $z$.

D: Chiarimento sull’aggregazione di caratteristiche

R: (Yann LeCun disegna la rappresentazione degli AE con sparsità di gruppo) Il codificatore produce la variabile latente $z$, che viene regolarizzata usando la norma $L_2$ delle caratteristiche aggregate. Questa $z$ è usata dal decodificatore per la ricostruzione delle immagini.

D: La regolarizzazione di gruppo aiuta nel raggruppamento di caratteristiche simili?

R: La risposta non è chiara, di lavoro su questo tema n’è stato fatto prima che ci fossero potenza computazionale o dati a disposizione. Queste tecniche non sono state più portate in primo piano.

Addestramento a livello d’immagine, filtri locali senza condivisione dei pesi

Non è chiaro se questi siano d’aiuto o meno. Le persone interessate in questo tema sono o interessate nel restauro d’immagini o un certo tipo di apprendimento auto-supervisionato. Ciò funzionerebbe bene se il dataset fosse molto piccolo. Quando si hanno dei codificatori e decodificatori che sono convoluzionali che si addestrano con sparsità di gruppo su cellule complesse, dopo che è stato fatto il pre-addestramento, si prende il decodificatore e lo si scarta, si conserva il codificatore e lo si utilizza come estrattore di caratteristiche, ad esempio come primo strato di una rete convoluzionale, a cui si aggiungono ulteriori strati convoluzionali di seguito.

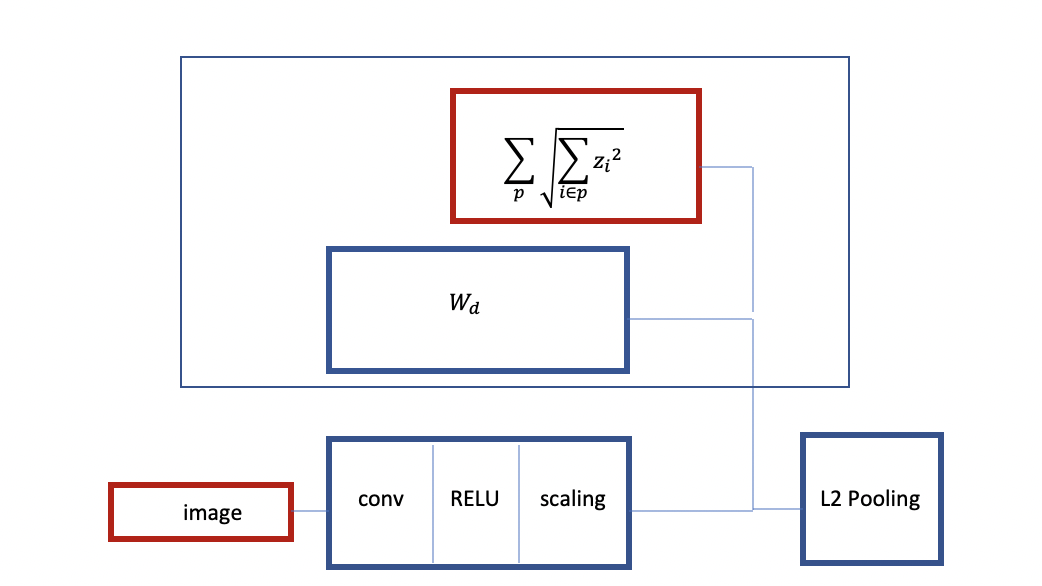
Fig. 3: struttura di uno strato convoluzionale ReLU con sparsità di gruppo

Come si può notare sopra, s’inizia con un’immagine, si ha a disposizione un codificatore che è sostanzialmente uno strato convoluzionale ReLU e, di seguito, una sorta di strato di riscalamento. Si addestra la rete con sparsità di gruppo. Si ha un decodificatore lineare e un criterio di raggruppamento per 1. Si considera la sparsità di gruppo come un regolarizzatore. Ciò equivale ad effettuare un’aggregazione tramite norma $L_2$ con un’architettura simile alla sparsità di gruppo.

Si può anche addestrare un’altra istanza della medesima rete. Stavolta, si possono aggiungere più strati e avere un decodificatore con l’aggregazione $L_2$ e un criterio di sparsità, lo si addestra a ricostruire l’input con un’aggregazione alla fine. Questo creerà una rete convoluzionale pre-addestrata di due strati. Questa procedura viene anche chiamata “autoencoder sovrapposti”. La caratteristica pricipale qui è che la rete è addestrata per produrre caratteristiche invarianti con sparsità di gruppo.

D: Si dovrebbero utilizzare tutti i possibili sotto-alberi come gruppi?

R: Sta a voi decidere, si possono avere anche alberi multipli se lo si desidera. Si pssono addestrare alberi più grandi del necessario, e poi rimuovere i rami non utilizzati.

Fig. 4: addestramento a livello d'immagine, filtri locali senza condivisione dei pesi

Questi sono chiamati pattern a girandola. Sono una tipologia di organizzazione delle caratteristiche. L’orientamento varia in continuazione come ci si muove attorno ai punti rossi. Se prendiamo uno di questi punti rossi e ci disegnamo attorno un piccolo cerchio, noteremo che l’orientamento dell’estrattore sembra variare in continuazione come ci si muove attorno. Trend simili si sono notati anche nel cervello.

D: Il termine relativo alla sparsità di gruppo è addestrato affinché assuma valori piccoli?

È un regolarizzatore. Il termine in sé non viene addestrato, è fisso. È la norma $L_2$ dei gruppi, e i gruppi sono predeterminati. Ma, siccome questo è un criterio, determina che cosa il codificatore e il decodificatore faranno e che tipologia di caratteristiche saranno quindi estratte.

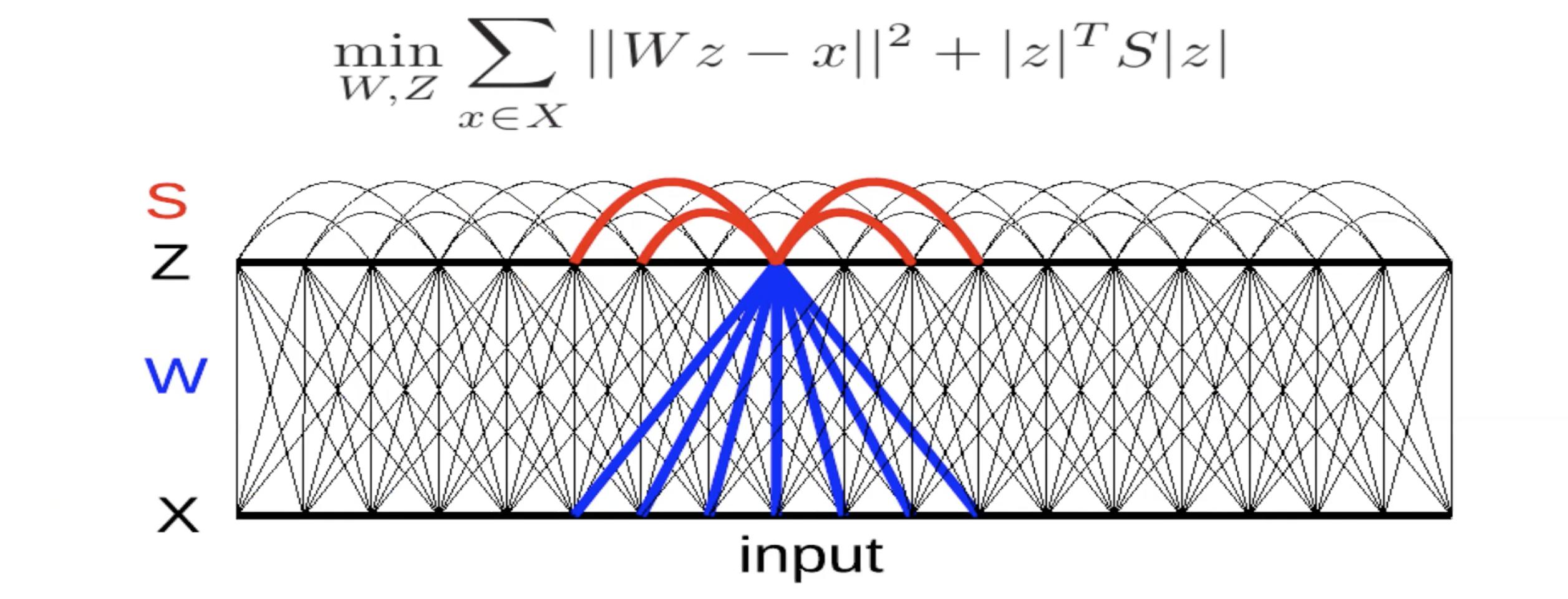
Fig. 5: caratteristiche invarianti ottenute tramite inibizione laterale

Qui c’è un decodificatore lineare con errore quadratico di ricostruzione. C’è un criterio nell’energia. La matrice $S$ è determinata a mano o addestrata per massimizzare questo termine. Se i termini in $S$ sono grandi e positivi, ne consegue che il sistema non vuole che $z_i$ e $z_j$ si attivino contemporaneamente. Di conseguenza, è una specie di mutua inibizione (chiamata inibizione naturale nelle neuroscienze). Di conseguenza, si cerca di trovare un valore di $S$ più grande possibile.

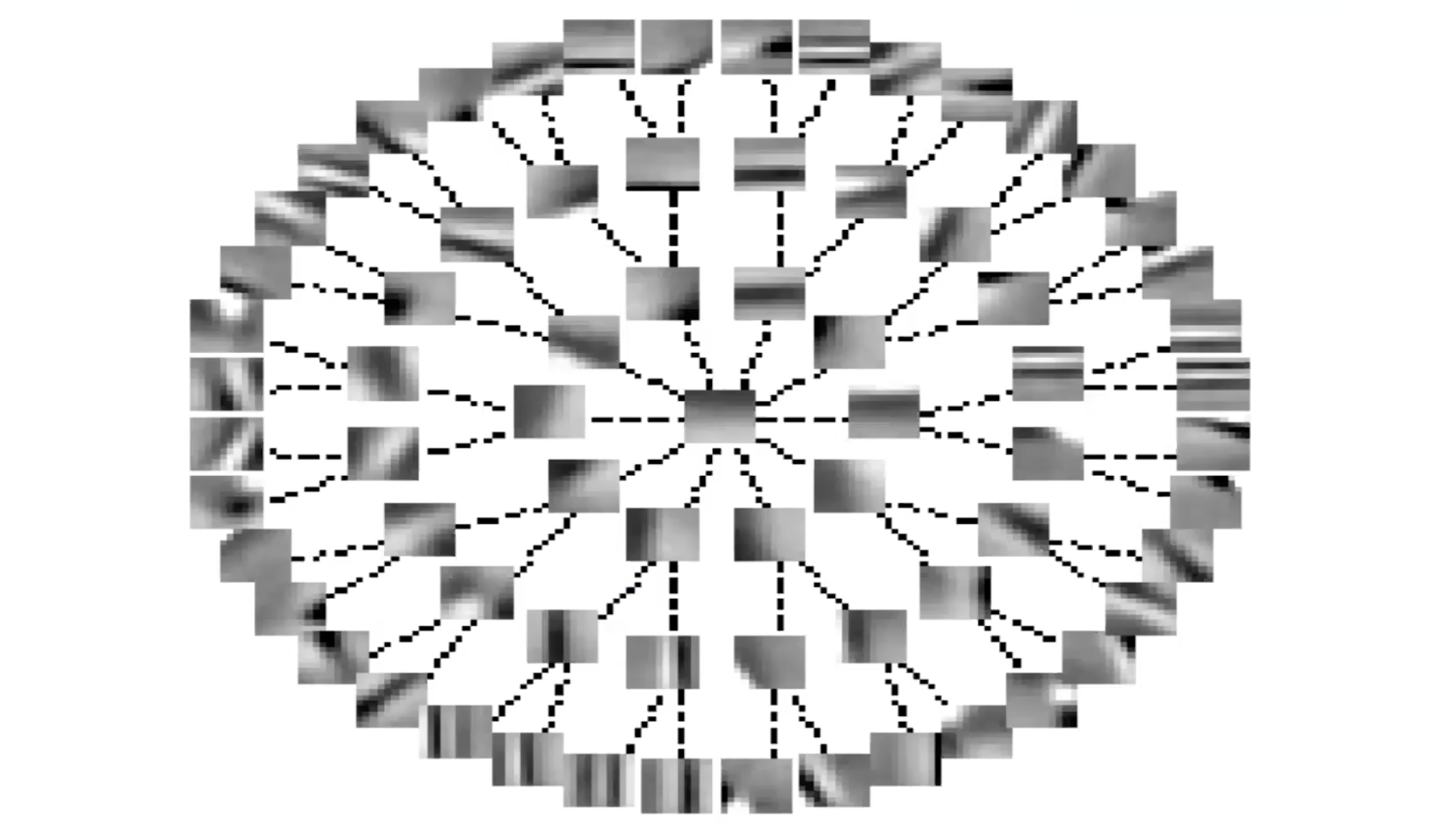
Fig. 6: caratteristiche invarianti ottenute tramite inibizione laterale (forma ad albero)

Organizzando $S$ nei termini di un albero, le linee rappresentano i termini a zero nella matrice $S$. La mancanza di una linea corrisponde ad un termine non-nullo. Quindi, ogni caratteristica inibisce tutte le altre, ad eccezione di quelle che si trovano più in alto o più in basso nell’albero. Ciò è come la converse della sparsità di gruppo.

Si nota nuovamente come i sistemi organizzano le caratteristiche in una maniera più o meno continua. Le caratteristiche lungo i rami di un albero rappresentano le stesse caratteristiche con diversi livelli di selettività. Le caratteristiche lungo la periferia variano più o meno in maniera continua perché non c’è inibizione.

Per addestrare questo sistema, ad ogni iterazione si dà come input al modello una $x$ e si trova un $z$ che minimizzi la funzione di energia. Quindi si opera un passo della discesa del gradiente per aggiornare $W$. Si può anche operare un passo di ascesa del gradiente per rendere i termini di $S$ più grandi.