Modelli generativi - autoencoder variazionali

Introduzione agli autoencoder variazionali (Variational Autoencoders, VAE)

Riepilogo: autoencoder (AE)

Per ricapitolare a grandi linee, una forma molto semplice di AE è composta come segue:

• Prima di tutto, l’autoencoder prende un input e lo mappa in uno stato nascosto tramite una trasformazione affine $\boldsymbol{h} = f(\boldsymbol{W}_h \boldsymbol{x} + \boldsymbol{b}_h)$, dove $f$ è una funzione di attivazione applicata elemento per elemento.
• Dopodiché, $\hat{\boldsymbol{x}} = g(\boldsymbol{W}_x \boldsymbol{h} + \boldsymbol{b}_x)$, dove $g$ è una funzione di attivazione. Questa è la fase di decodifica.

Per una spiegazione dettagliata, fare riferimento alle note della settimana 7.

Intuizione dietro ai VAE e paragone con gli autoencoder classici

Di seguito, introdurremo gli autoencoder variazionali (VAE), un tipo di modello generativo. Per quale motivo ci interessiamo ai modelli generativi? Per rispondere a ciò, i modelli discriminativi imparano ad effettuare previsioni data un’osservazione, ma i modelli generativi mirano a simulare il processo di generazione dei dati. Una consequenza è che i modelli generativi possono comprendere meglio le relazioni causali sottostanti, il che porta a una migliore generalizzazione.

Si noti che, sebbene VAE abbia gli autoencoder (AE) nel proprio nome (data la similarità strutturale o architettonica fra i due), gli AE e i VAE hanno formulazioni molto diverse. Si veda la Fig. 1 sotto:

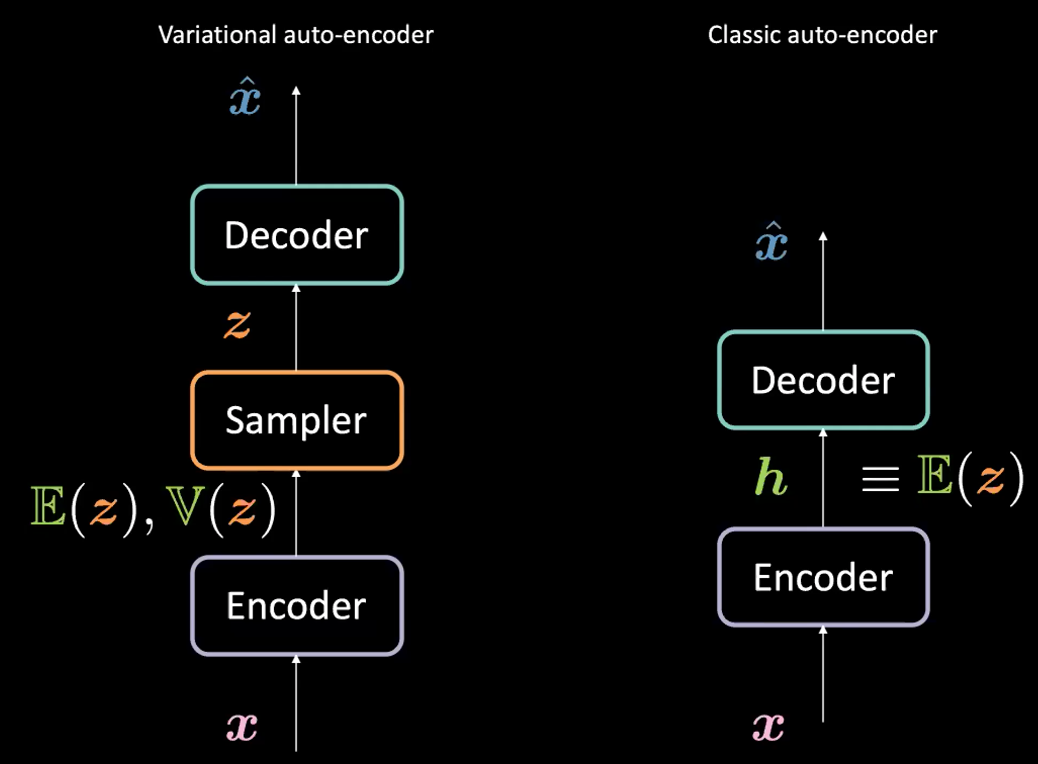
Fig. 1: VAE vs. AE classici

Qual è la differenza tra autoencoder variazionali (VAE) e autoencoder classici (AE)?

I VAE:

• Prima di tutto, la fase di codificazione: passiamo l’input $\boldsymbol{x}$ al codificatore (encoder). Anziché generare una rappresentazione nascosta $\boldsymbol{h}$ (il codice), il codice nei VAE comprende due elementi: $\mathbb{E}(\boldsymbol{z})$ e $\mathbb{V}(\boldsymbol{z})$ dove $\boldsymbol{z}$ è la variabile aleatoria latente che si comporta secondo una distribuzione gaussiana con media $\mathbb{E}(\boldsymbol{z})$ e varianza $\mathbb{V}(\boldsymbol{z})$. Si noti che nella pratica si utilizzano distribuzioni gaussiane, ma potrebbero teoricamente esserne usate di altre.
• Il codificatore sarà una funzione da $\mathcal{X}$ toa $\mathbb{R}^{2d}$: $\boldsymbol{x} \mapsto \boldsymbol{h}$ (qui denotiamo con $\boldsymbol{h}$ la concatenazione di $\mathbb{E}(\boldsymbol{z})$ e $\mathbb{V}(\boldsymbol{z})$).
• Dopodiché, opereremo un campionamento di $\boldsymbol{z}$ dalla distribuzione di cui sopra, parametrizzata dal codificatore; nello specifico, $\mathbb{E}(\boldsymbol{z})$ e $\mathbb{V}(\boldsymbol{z})$ sono passate ad un campionatore (sampler) per generare la variabile latente $\boldsymbol{z}$.
• Poi, $\boldsymbol{z}$ viene passato al decodificatore (decoder) per generare $\hat{\boldsymbol{x}}$.
• Il decodificatore sarà una funzione da $\mathcal{Z}$ a $\mathbb{R}^{n}$: $\boldsymbol{z} \mapsto \boldsymbol{\hat{x}}$.

Di fatto, per un autoencoder classico, possiamo pensare a $\boldsymbol{h}$ come il solo vettore $\E(\boldsymbol{z})$ nella formulazione del VAE. In breve, la differenza principale fra i VAE e gli AE è che i primi hanno un buon spazio latente che permette l’attuazione di processi generativi.

La funzione obiettivo (perdita) dei VAE

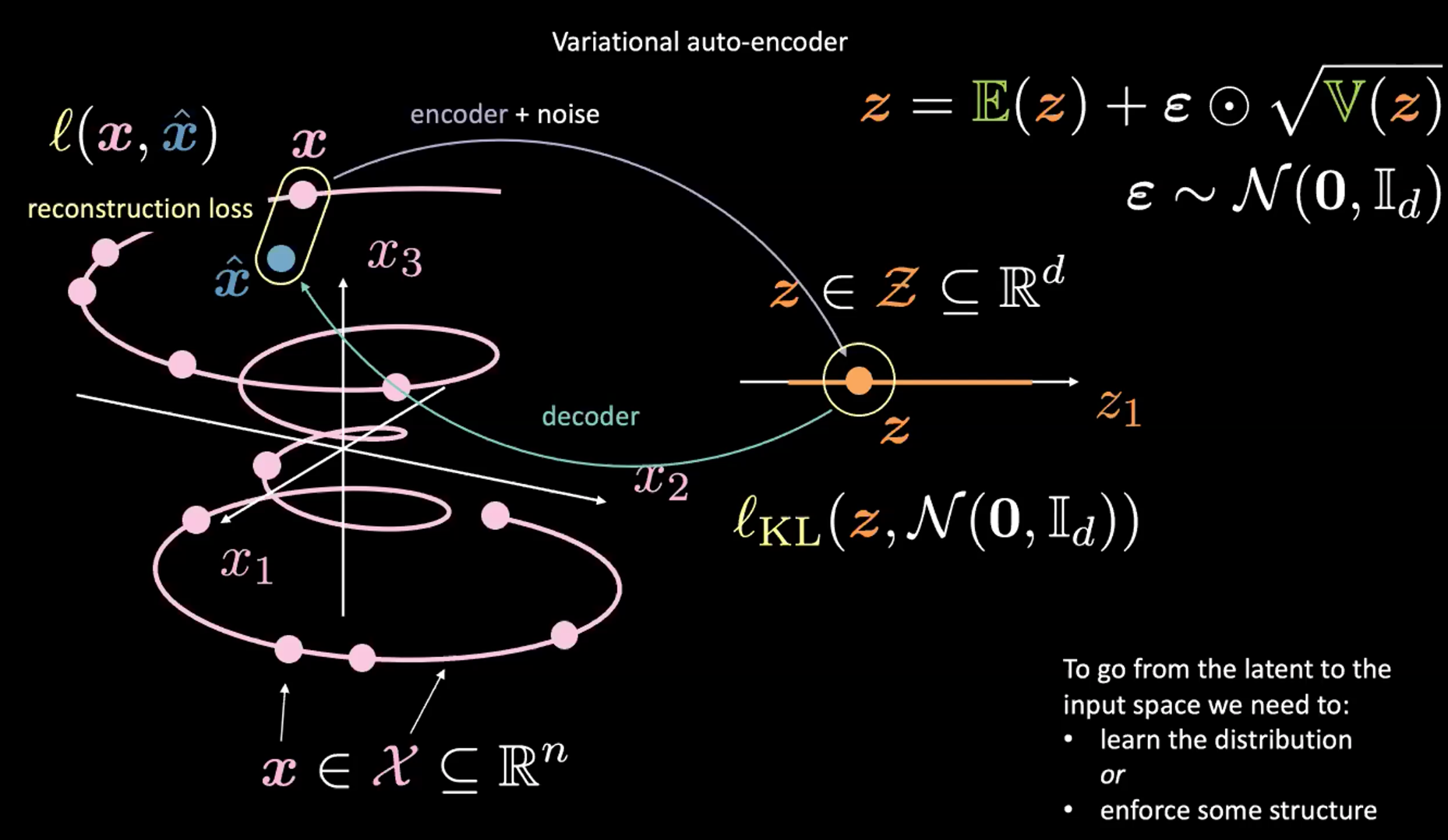
Fig. 2: mappatura dallo spazio di input allo spazio latente

Si osservi la Fig. 2 qui sopra. Per ora, s’ignori l’angolo in alto a destra (che è il trucco della riparametrizzazione che verrà spiegato nella sezione successiva).

Prima di tutto, codifichiamo dallo spazio di input (a sinistra) allo spazio latente (a destra) tramite il codificatore e del rumore. Dopodiché, decodifichiamo dallo spazio latente (a destra) allo spazio di output (a sinistra). Per passare dallo spazio latente a quello d’input (passaggio che rappresenta il processo generativo) necessitiamo o di imparare la distribuzione (del codice latente) o di vincolare una certa struttura sullo spazio latente.

Come al solito, per addestrare un VAE, minimizziamo una funzione di perdita. La funzione di perdita è composta da un termine di ricostruzione e da un termine di regolarizzazione.

• Il termine di ricostruzione si trova nello strato finale (parte sinistra della figura). Questo corrisponde a $l(\boldsymbol{x}, \hat{\boldsymbol{x}})$ nella figura.
• Il termine di regolarizzazione si trova nello spazio latente, per imporre una struttura gaussiana specifica nello spazio latente (lato destro della figura). Operiamo ciò utilizzando un termine di penalità $l_{KL}(\boldsymbol{z}, \mathcal{N}(\boldsymbol{0}, \boldsymbol{I}_d))$. In assenza di questo termine, il VAE si comporterebbe come un AE classico, il che potrebbe portare a sovradattamento (overfitting) e non avremmo a disposizione le proprietà generative alle quali siamo interessati.

Discussione sul campionamento di $\boldsymbol{z}$ (trucco della riparametrizzazione – reparameterization trick)

Come operiamo il campionamento dalla distribuzione restituita dal codificatore nei VAE? Come dalla sezione precedente, campioniamo dalla distribuzione gaussiana, al fine di ottenere $\boldsymbol{z}$. Tuttavia, ciò è problematico, perché quando operiamo la discesa del gradiente per addestrare il modello VAE, non sappiamo come fare la retropropagazione attraverso il modulo di campionamento.

Invece, usiamo il trucco della riparametrizzazione per “campionare” $\boldsymbol{z}$. Utilizziamo $\boldsymbol{z} = \mathbb{E}(\boldsymbol{z}) + \boldsymbol{\epsilon} \odot \sqrt{\mathbb{V}(\boldsymbol{z})}$ dove $\epsilon\sim \mathcal{N}(\boldsymbol{0}, \boldsymbol{I}_d)$. In questo caso, la retropropagazione durante l’addestramento è possibile. Nello specifico, il gradiente passerà attraverso la moltiplicazione elemento per elemento e all’addizione come nell’equazione qui sopra.

Dissezione della funzione di perdita dei VAE

Visualizzazioni delle stime della variabile latente e dalla perdita di ricostruzione

Come prima citato, la funzione di perdita dei VAE è composta di due parti: un termine di ricostruzione e un termine di regolarizzazione. Possiamo scrivere ciò come

Per visualizzare lo scopo di ogni termine nella funzione di perdita, possiamo pensare ad ogni valore stimato $\boldsymbol{z}$ come un cerchio nello spazio $2D$, dove il centro del cerchio è $\mathbb{E}(\boldsymbol{z})$ e l’area circostante rappresenta i possibili valori di $\boldsymbol{z}$, area determinata da $\mathbb{V}(\boldsymbol{z})$.

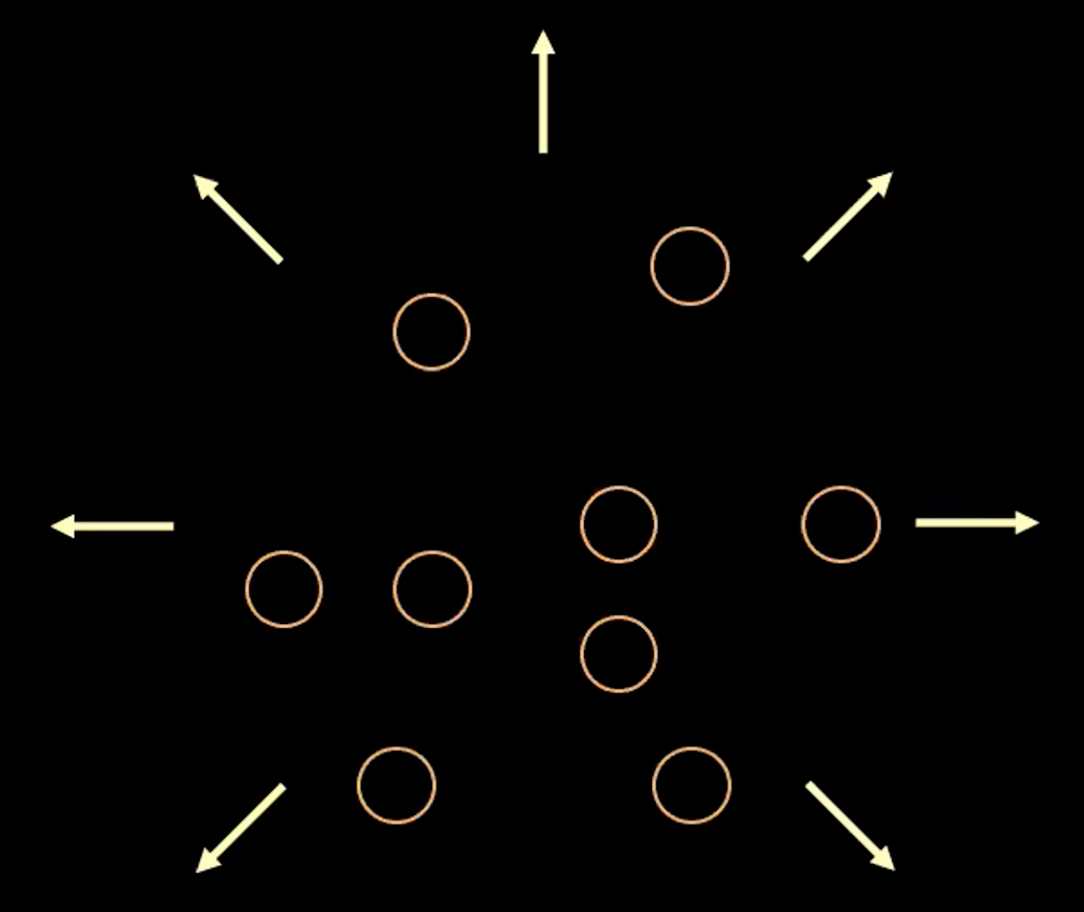
Fig. 3: visualizzazione del vettore $z$ come bolle nello spazio latente

Nella Fig. 3 qui sopra, ogni bolla rappresenta una regione stimata di $\boldsymbol{z}$ e le frecce rappresentano come il termine di ricostruzione “allontani” ogni valore stimato dagli altri, fenomeno di cui spieghiamo di più qui sotto.

Se c’è una sovrapposizione fra qualsiasi due stime di $z$ (visivamente, se due bolle si sovrappongono) ciò causa ambiguità al processo di ricostruzione perché i punti facenti parte dell’intersezione possono essere mappati a entrambi gli input originari. Quindi la perdita di ricostruzione allontanerà tali punti.

Ad ogni modo, se usiamo solo la perdita di ricostruzione, le stime continueranno ad essere mutuamente allontanate e il sistema potrebbe divergere. Qui il termine di penalità entra in gioco

Nota: per input binari, la perdita di ricostruzione è

e per input a valori reali è

Il termine di penalità

Il secondo termine è l’entropia relativa (una misura di distanza fra due distribuzioni) tra $\boldsymbol{z}$, che proviene da una gaussiana con media $\mathbb{E}(\boldsymbol{z})$ e varianza $\mathbb{V}(\boldsymbol{z})$, e la distribuzione normale standard. Se espandiamo con questo termine, la funzione di perdita diviene

dove ogni espressione nella sommatoria ha quattro termini. Sotto trascriviamo e rendiamo in un grafico il primo di questi termini (v. Fig. 4)

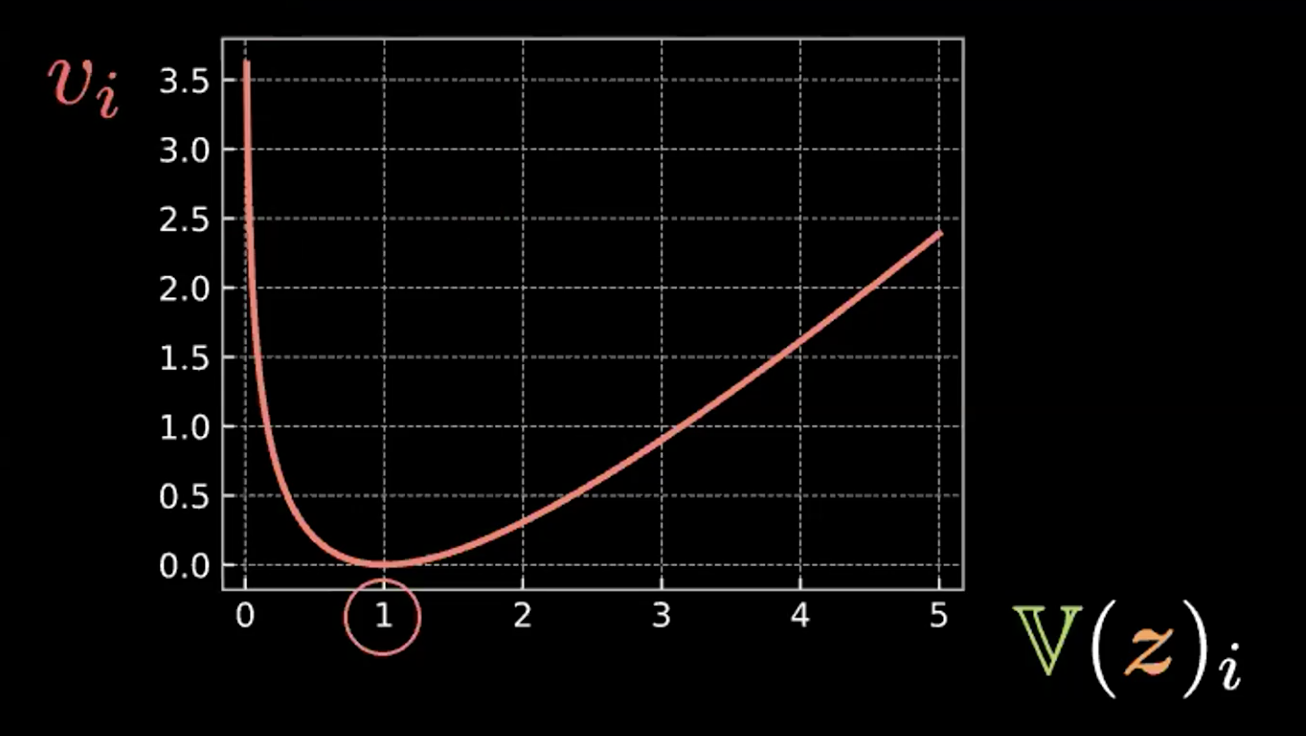
Fig. 4: grafico visualizzante l'effetto dell'entropia nel forzare le bolle ad avere varianza pari a 1

Così possiamo vedere che questa espressione è minimizzata quando $z_i$ ha varianza 1. Quindi, il nostro termine di penalità terrà la varianza della stima della variabile latente circa attorno a 1. Visivamente, ciò si traduce nel fatto che le nostre bolle di cui sopra avranno un raggio di circa 1.

L’ultimo termine, $\mathbb{E}(z_i)^2$, minimizza la distanza fra $z_i$ e quindi ne previene la divergenza incoraggiata dal termine di ricostruzione.

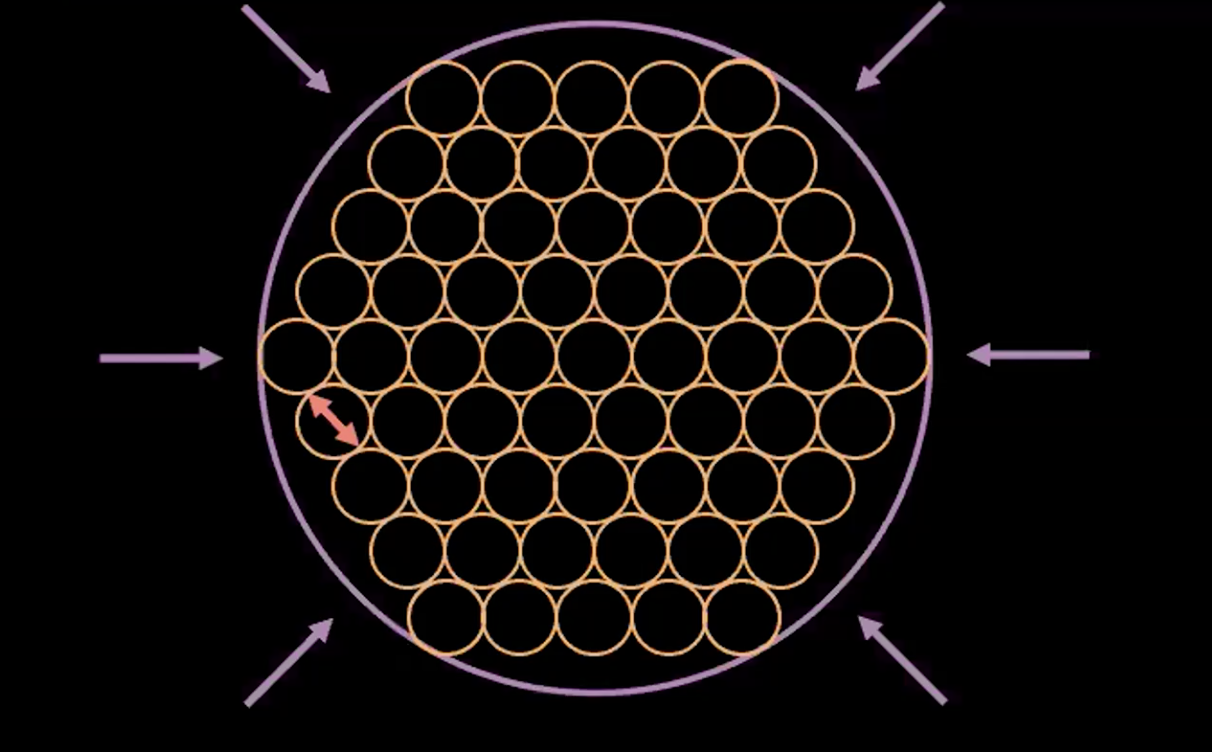
Fig. 5: interpretazione della VAE come "bolla di bolle"

La Fig. 5 qui sopra mostra come la perdita del VAE spinge le variabili latenti stimate il più vicino possibile senza sovrapposizioni, tenendo la varianza stimata di ogni punto attorno a uno.

Nota: il $\beta$ nella funzione di perdita del VAE è un iperparametro che detta quanto peso dare al termine di ricostruzione e a quello di penalità.

Implementazione di un autoencoder variazionale

Il notebook di Jupyter può essere reperito qui.

In questo notebook, implementiamo un VAE e lo addestriamo sul dataset MNIST. Quindi campioniamo $\boldsymbol{z}$ da una distribuzione normale e lo diamo come input al decodificatore e compariamo il risultato. Infine, vediamo come $\boldsymbol{z}$ cambia in proiezioni bidimensionali.

Nota: nel dataset di MNIST che utilizziamo, i valori dei pixel sono stati normalizzati affinché rientrino nel range $[0, 1]$.

Il codificatore e il decodificatore

1. Definiamo il codificatore (encoder) e il decodificatore (decoder) nel nostro modulo VAE.
2. Nell’ultimo strato lineare del codificatore, poniamo la grandezza dell’output pari a $2d$: i primi $d$ valori rappresentano le medie; i successivi $d$ sono le varianze. Campioniamo $boldsymbol{z} \in R^d$ utilizzando media e varianza come spiegato nel trucco della riparametrizzazione prima citato.
3. Per l’ultimo strato lineare nel decodificatore, usiamo la funzione di attivazione sigmoidale così che possiamo ottenere output nel range $[0, 1]$, analogamente ai dati di input.

class VAE(nn.Module):
def __init__(self):
super().__init__()

self.encoder = nn.Sequential(
nn.Linear(784, d ** 2),
nn.ReLU(),
nn.Linear(d ** 2, d * 2)
)

self.decoder = nn.Sequential(
nn.Linear(d, d ** 2),
nn.ReLU(),
nn.Linear(d ** 2, 784),
nn.Sigmoid(),
)

La riparametrizzazione e la funzione forward

Per la funzione di riparametrizzazione reparametrise, se il modello è in modalità di addestramento (train), calcoliamo la deviazione standard (std) dalla varianza al logaritmo (logvar). Usiamo quest’ultima anziché la varianza perché vogliamo essere sicuri che la varianza non sia negativa, e prenderne il logaritmo ci assicura che abbiamo il range completo della varianza, il che si traduce in un addestramento più stabile.

Durante l’addestramento, reparametrise opererà il trucco della riparametrizzazione permettendoci di svolgere la retropropagazione. Connettendoci al concetto delle bolle, come spiegato nel corso della lezione, ogni volta che questa funzione viene chiamata, disegniamo un punto eps = std.data.new(std.size()).normal_(), così che, se lo facciamo 100 volte, otterremo 100 punti che grosso modo formano una sfera, perché stiamo campionando da una distribuzione normale; la linea di codice eps.mul(std).add_(mu) centrerà questa sfera in mu con raggio uguale a std.

Per quanto riguarda la funzione forward, prima computiamo mu (prima metà), poi la logvar (seconda metà) per il codificatore, dopodiché computiamo $\boldsymbol{z}$ tramite la funzione reparametrise. Infine, restituiamo l’output del decodificatore.

def reparameterise(self, mu, logvar):
if self.training:
std = logvar.mul(0.5).exp_()
eps = std.data.new(std.size()).normal_()
return eps.mul(std).add_(mu)
else:
return mu

def forward(self, x):
mu_logvar = self.encoder(x.view(-1, 784)).view(-1, 2, d)
mu = mu_logvar[:, 0, :]
logvar = mu_logvar[:, 1, :]
z = self.reparameterise(mu, logvar)
return self.decoder(z), mu, logvar

Funzione di perdita per il VAE

Qui definiamo l’errore di ricostruzione (entropia incrociata binaria – binary cross-entropy) e l’entropia relativa (penalità corrispondente alla divergenza di Kullback-Leibler).

def loss_function(x_hat, x, mu, logvar):
BCE = nn.functional.binary_cross_entropy(
x_hat, x.view(-1, 784), reduction='sum'
)
KLD = 0.5 * torch.sum(logvar.exp() - logvar - 1 + mu.pow(2))

return BCE + KLD

Generazione di nuove osservazioni

Dopo l’addestramento del nostro nodello, possiamo campionare un $z$ casuale dalla distribuzione normale e darlo come input al nostro decodificatore. Possiamo osservare, in Fig. 6, che alcuni di questi risultati non siano buoni in quanto il nostro decodificatore non ha “coperto” l’intero spazio latente. Ciò si può migliorare addestrando il modello per più epoche.

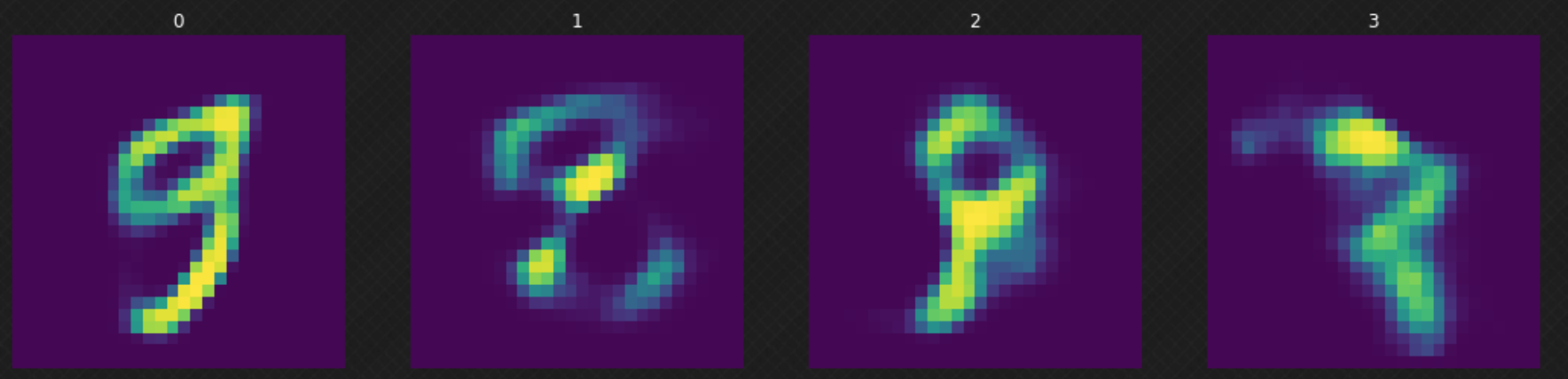
Fig. 6: movimenti casuali nello spazio latente

Possiamo osservare come vi siano delle fusioni fra cifre, il che non sarebbe stato possibile se avessimo usato un autoencoder. Possiamo vedere che, percorrendo lo spazio latente, l’output del decodificatore sembri ancora autentico. La Fig. 7 di sotto mostra la fusione della cifra $3$ nella cifra $8$.

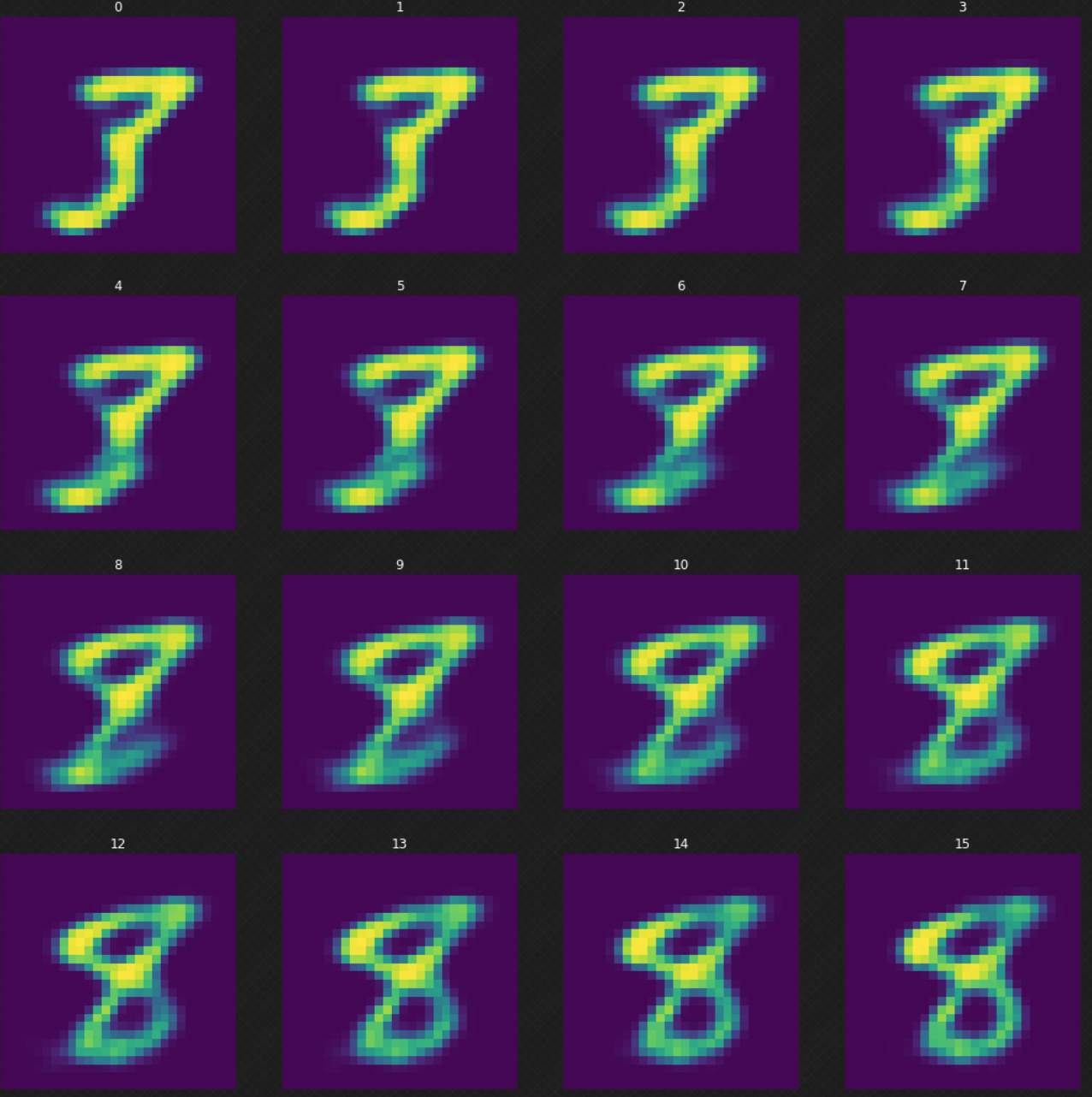
Fig. 7: fusione del 3 in 8

Proiezione delle medie

Infine, diamo un’occhiata a come lo spazio latente varia durante/dopo l’addestramento. I grafici in Fig. 8 rappresentano la media dell’output del codificatore, proiettate nello spazio 2D, dove ogni colore rappresenta una cifra. Possiamo vedere che all’epoca 0 le classi sono sparpagliate ovunque, con poca concentrazione. Come il modello viene addestrato, lo spazio latente diviene meglio definito e le classi (le cifre) iniziano a formare dei cluster.

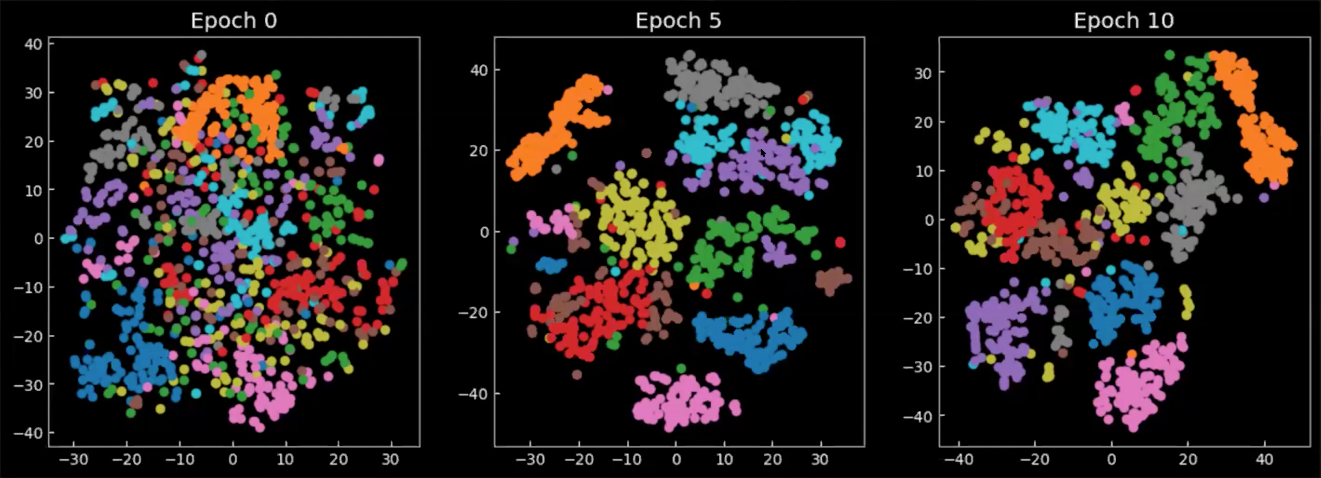
Fig. 8: proiezione in 2D delle medie $\E(\vect{z})$ nello spazio latente