Modelli ad energia a variabile latente regolarizzata

EBM a variabile latente regolarizzata

I modelli a variabile latente sono capaci di produrre una distribuzione di previsioni $\overline{y}$ condizionate a un input osservato $x$ e una variabile latente aggiuntiva $z$. I modelli basati sull’energia possono anche contenere variabili latenti:

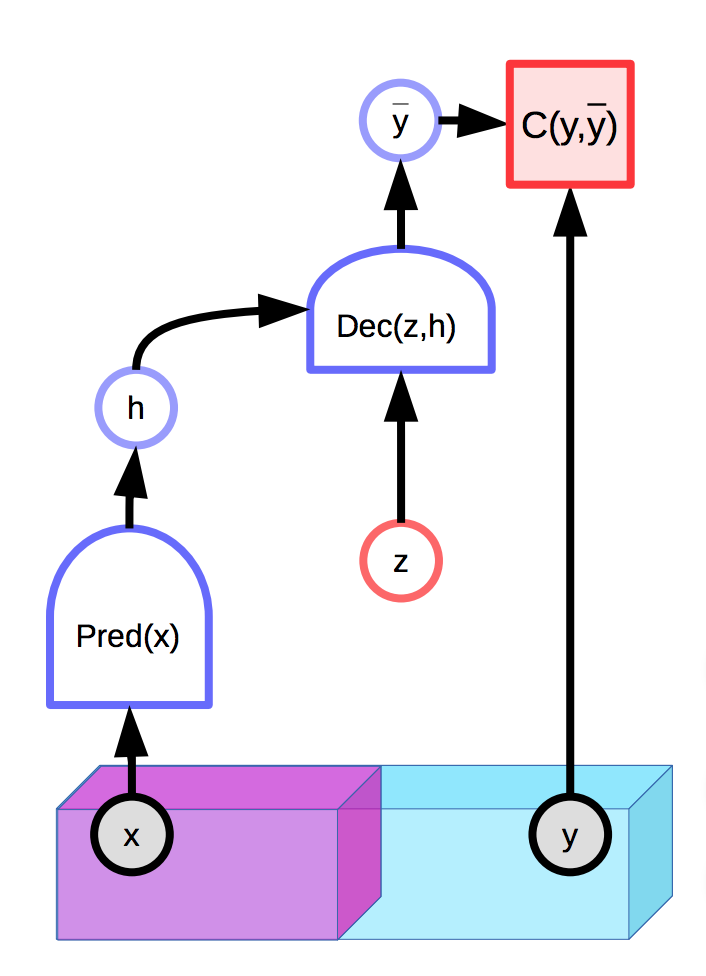
Fig. 1: Esempio di EBM con variabile latente

Si vedano gli appunti della precedente lezione per maggiori dettagli.

Sfortunatamente, se la variabile latente $z$ ha troppa potenza espressiva nella produzione della previsione finale $\overline{y}$, ogni output reale $y$ verrà perfettamente ricostruito a partire dall’input $x$ tramite un $z$ scelto in maniera appropriata. Ciò significa che la funzione di energia sarà 0 ovunque, poiché l’energia è ottimizzata su entrambi gli $y$ e i $z$ durante l’inferenza.

Una soluzione naturale è limitare la capacità d’informazione della variabile latente $z$. Un modo per ottenere ciò è tramite regolarizzazione della variabile latente:

Questo metodo limiterà il volume dello spazio di $z$ a valori molto piccoli; valori che, a loro volta, determineranno lo spazio di $y$ a bassa energia. Il valore di $\lambda$ controlla questo compromesso. Un esempio utile per $R$ è la norma $L_1$, la quale può essere vista come un’approssimazione quasi-ovunque differenziabile della dimensione effettiva. Aggiungendo rumore a $z$ contemporaneamente limitandone la sua norma $L_2$ può anche risultare nella limitazione del suo contenuto informativo.

Codificazione sparsa (Sparse Coding)

La codificazione sparsa è un esempio di EBM a variabile latente regolarizzata e incondizionata: essenzialmente, il suo scopo è quello di approssimare i dati con una funzione lineare a tratti.

Il vettore $n$-dimensionale $z$ tenderà ad avere un numero massimo di componenti non-nulle $m « n$; quindi, ogni $Wz$ sarà composto da elementi del sottospazio generato da $m$ colonne di $W$.

Dopo ogni passo di ottimizzazione, la matrice $W$ e la variabile latente $z$ vengono normalizzate dalla somma delle norme $L_2$ delle colonne di $W$. Ciò garantisce che $W$ e $z$ non divergano a infinito o a zero.

FISTA

Fig. 2: grafico computazionale di FISTA

FISTA (Fast ISTA) è un algoritmo che ottimizza la funzione di energia per codificazione sparsa $E(y,z)$ rispetto $z$ ottimizzando in maniera alternata i due termini $\Vert y - Wz\Vert^2$ e $\lambda \Vert z\Vert_{L^1}$. Inizializziamo $Z(0)$ e aggiorniamo $Z$ in maniera iterativa secondo la regola seguente:

L’espressione interna $Z(t) - \frac{1}{L}W_d^\top(W_dZ(t) - Y)$ è un passo del gradiente per il termine $\Vert y - Wz\Vert^2$. La funzione di contrazione $\text{Shrinkage}$ trasla, dopodiché, i valori verso 0, poi ottimizza il termine $\lambda \Vert z\Vert_{L_1}$.

LISTA

FISTA è computazionalmente troppo costoso da applicare a grandi insiemi di dati con alta dimensionalità (ad esempio, le immagini). Un modo per renderlo più efficiente è invece quello di addestrare una rete per predire la variabile latente $z$ ottimale:

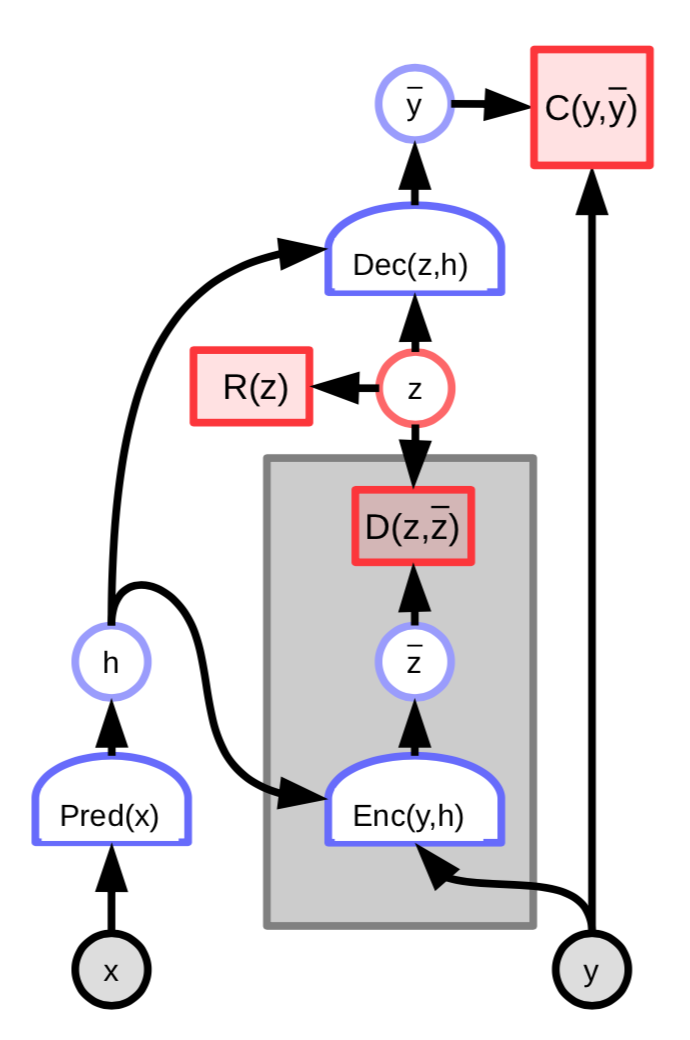
Fig. 3: EBM con codificatore della variabile latente

L’energia di questa architettura include un termine aggiuntivo per misurare la differenza fra la variabile latente prevista $\overline z$ e la variabile latente ottimale $z$:

Possiamo inoltre definire

e quindi scrivere

Questa regola di aggiornamento può essere interpretata come una rete ricorsiva, il che dà l’idea che possiamo invece apprendere i parametri $W_e$ i quali determinano iterativamente la variabile latente $z$. La rete viene fatta agire per un numero fissato di istanti temporali $K$ e i gradienti di $W_e$ sono calcolati usando la classica retropropagazione nel tempo. La rete addestrata produce quindi un buon $z$ in un numero minore d’iterazioni rispetto all’algoritmo FISTA.

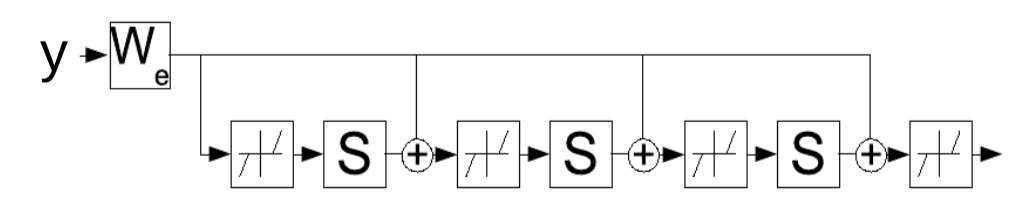
Fig. 4: LISTA visualizzata come una rete ricorrente dispiegata nel tempo.

Esempi di codificazione sparsa

Quando un sistema di codificazione sparsa con vettore latente di 256 dimensioni viene applicato alle cifre manoscritte di MNIST, impara un insieme di 256 tratti che possono essere combinati in maniera lineare per riprodurre quasi perfettamente l’intero dataset di addestramento. Il regolarizzatore sparso assicura che essi possano essere riprodotti a partire da un piccolo numero di tratti.

Fig. 5: codificatore sparso su MNIST. Ogni immagine è una colonna addestrata di $W$.

Quando un sistema di codificazione sparsa è addestrato su pezzi d’immagini naturali, le caratteristiche apprese sono filtri di Gabor, ovvero bordi orientati. Queste caratteristiche assomigliano a quelle imparate nelle prime parti dei sistemi visivi animali.

Codificazione sparsa convoluzionale

Supponiamo di avere un’immagine e una mappa delle caratteristiche ($z_1z_2…z_n$) dell’immagine. Possiamo quindi operare una convoluzione ($*$) su ciascuna delle mappe delle caratteristiche con un filtro $K_i$. Conseguentemente, la ricostruzione può essere calcolata semplicemente come:

Ciò differisce dalla codificazione sparsa originale, dove la ricostruzione era effettuata come $Y=\sum_{i}W_iZ_i$. Nella codificazione sparsa regolare, abbiamo una somma pesata di colonne dove i pesi sono i coefficienti di $Z_i$. Nella codificazione sparsa convoluzionale, è ancora un’operazione lineare, ma la matrice-dizionario ora è un insieme di mappe delle caratteristiche le quali sono convolute con ogni filtro; infine, sommiamo i risultati delle convoluzioni.

Autoencoder convoluzionale sparso su immagini naturali

Fig. 6 filtri e funzioni di base ottenute. Decodificatore convoluzionale lineare

I filtri nel codificatore e nel codificatore appaiono molto simili. Il codificatore è semplicemente una convoluzione seguita da non-linearità e quindi uno strato diagonale per variare la scala. Dopodiché la sparsità è imposta dal vincolo del codice. Il decodificatore è nient’altro che un decodificatore lineare convoluzionale e la ricostruzione utilizzata è l’errore al quadrato.

Di conseguenza, se imponiamo che ci sia solo un filtro, allora questo sarà del tipo center-surround. Con due filtri, possiamo ottenere dei filtri dalle forme bizzarre. Con quattro filtri, otteniamo bordi orientati (orizzontali e verticali); abbiamo due polarità per ogni filtro. Con otto filtri, possiamo ottenere bordi orientati in 8 orientamenti diversi. Con 16, otteniamo più orientamenti compresi i centers-around. All’aumentare del numero di filtri, otteniamo filtri diversi in aggiunta a quelli per i bordi orientati; ad esempio filtri per il riconoscimento di reticoli (grating), centers-around, ecc.

Questo fenomeno sembra essere interessante in quanto è simile a quanto si osserva nella corteccia visiva. Questa è quindi un’indicazione che possiamo apprendere caratteristiche molto buone in una maniera completamente non-supervisionata.

Come uso secondario, se prendiamo queste caratteristiche e le utilizziamo in una rete convoluzionale e le addestriamo su un qualche compito, non otteniamo necessariamente risultati migliori rispetto all’addestramento della rete da zero. Comunque, ci sono certe situazioni in cui ciò può aiutare a migliorare le performance. Ad esempio, nei casi dove il numero di istanze non è molto grande o ci sono poche categorie, addestrando in maniera completamente supervisionata, otteniamo delle caratteristiche degeneri.

Fig. 7 codificazione convoluzionale sparsa su un'immagine a colori

La figura qui sopra rappresenta un altro esempio su un’immagine a colori. Il filtro di decodificazione (a destra) ha dimensione 9 per 9. Questo filtro viene applicato in maniera convoluzionale sull’intera immagine. L’immagine a sinistra è del codice sparso ottenuto dal codificatore. Il vettore $Z$ è molto sparso: ci sono pochissime componenti che sono bianche o nere (non grigie).

Autoencoder variazionali (Variational Autoencoder)

Gli autoencoder variazionali hanno un’architettura simile agli EBM con variabile latente regolarizzata, con l’eccezione della sparsità. Negli autoencoder variazionali, il contenuto informativo del codice è limitato dalla rumorosità.

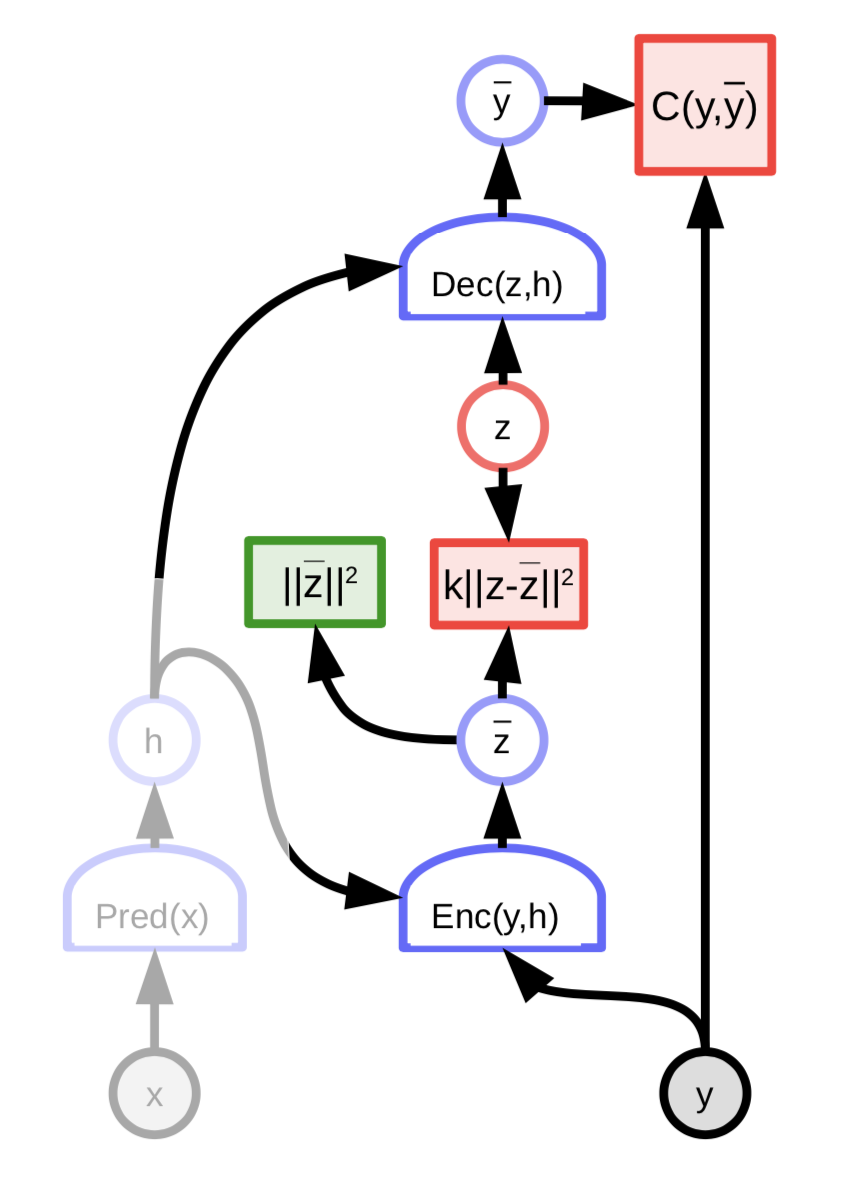
Fig. 8: architettura di un *autoencoder* variazionale

La variabile latente $z$ non è ottenuta minimizzando la funzione di energia rispetto a $z$; invece, la funzione di energia è visualizzata tramite il campionamento casuale di $z$ secondo una distribuzione, collegata a ${\overline z}$, il cui logaritmo rappresenta il costo. La distribuzione è una gaussiana con media ${\overline z}$; ciò risulta nell’aggiunta di rumore a ${\overline z}$.

I vettori della codifica con aggiunta di rumore gaussiano possono essere visualizzati come sfere sfocate, come mostrato in Fig. 9(a).

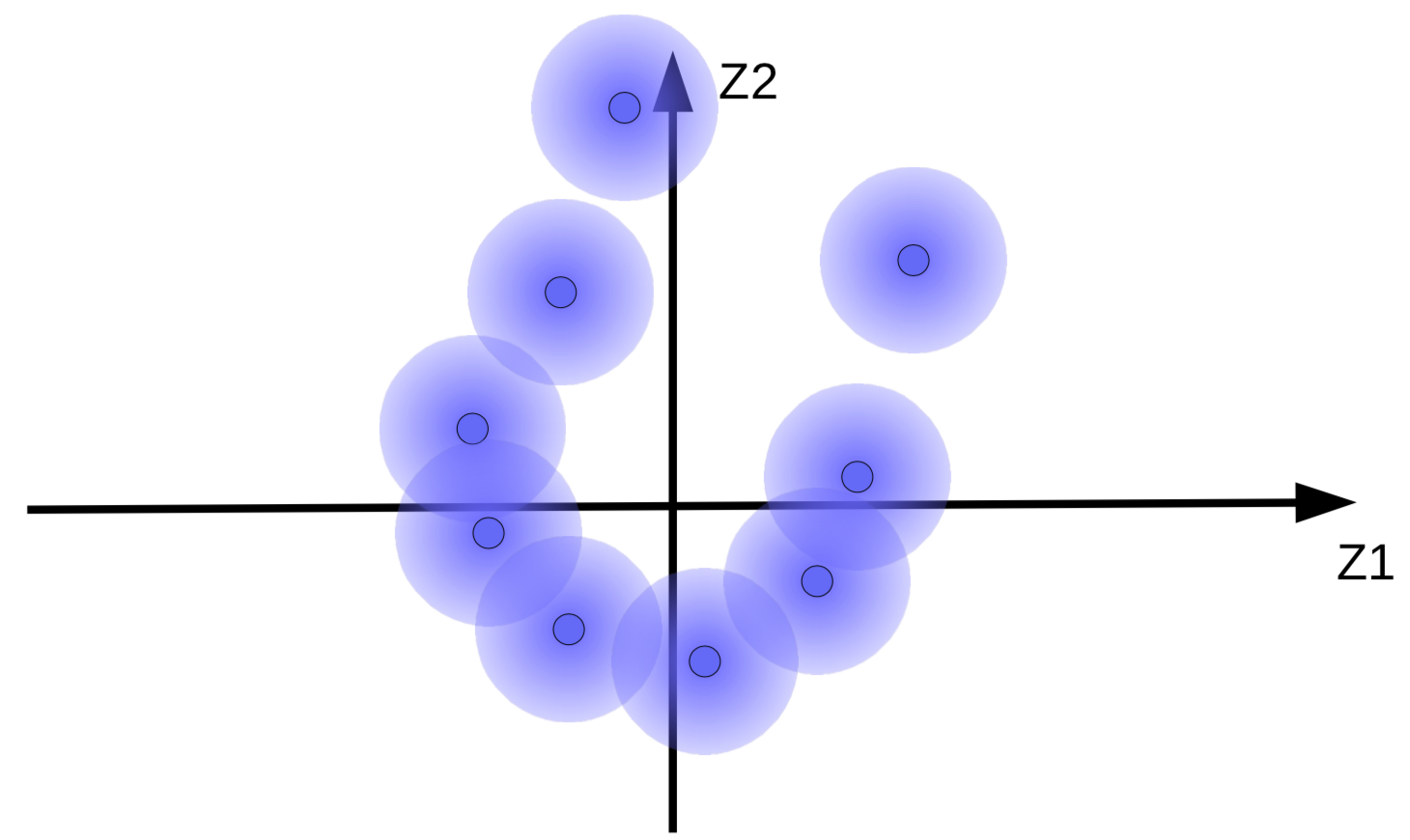(a) insieme originale di sfere sfocate

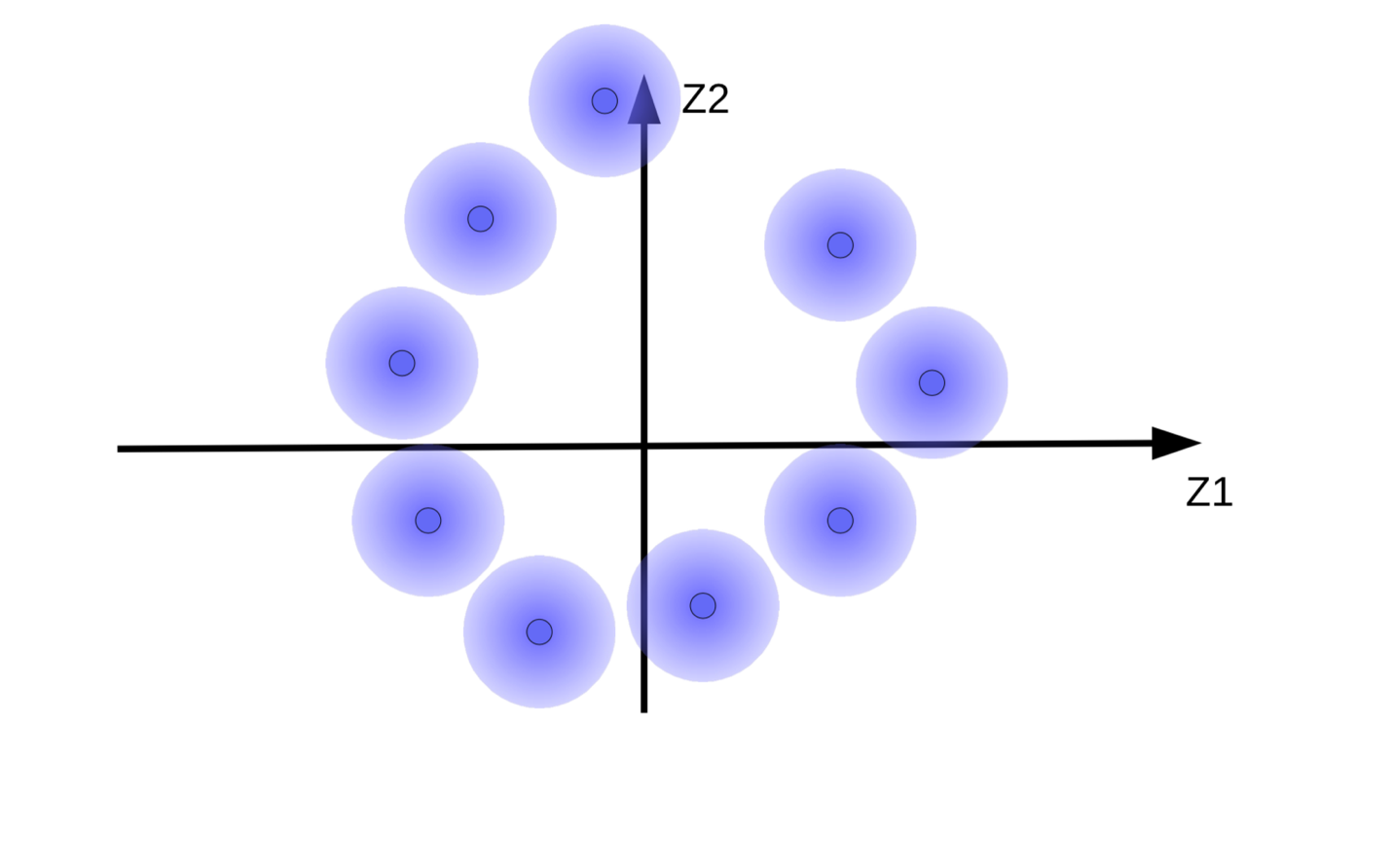(b) movimento delle sfere sfocate per effetto della minimizzazione di energia in assenza di regolarizzazione

Il sistema cerca di rendere il vettore della codifica $\overline z}$ più grande possibile in modo da limitare al massimo l’effetto del rumore $z$. Ciò risulta in una sfera sfocata che si allontana dall’origine come mostrato in Fig. 9(b). Un’altra ragione per cui il sistema cerca di rendere il vettore della codifica grande è per prevenire la sovrapposizione delle sfere sfocate, il che creerebbe al decodificatore confusione fra le diverse istanze durante la fase di ricostruzione.

Tuttavia, si vuole che le sfere sfocate si concentrino attorno una varietà dei dati, se ce n’è una. Di conseguenza, i vettori delle codifiche vengono regolarizzati in modo tale da avere una media e una varianza vicine a zero. Per fare ciò, le “colleghiamo” all’origine con una molla, come mostra la Fig. 10.

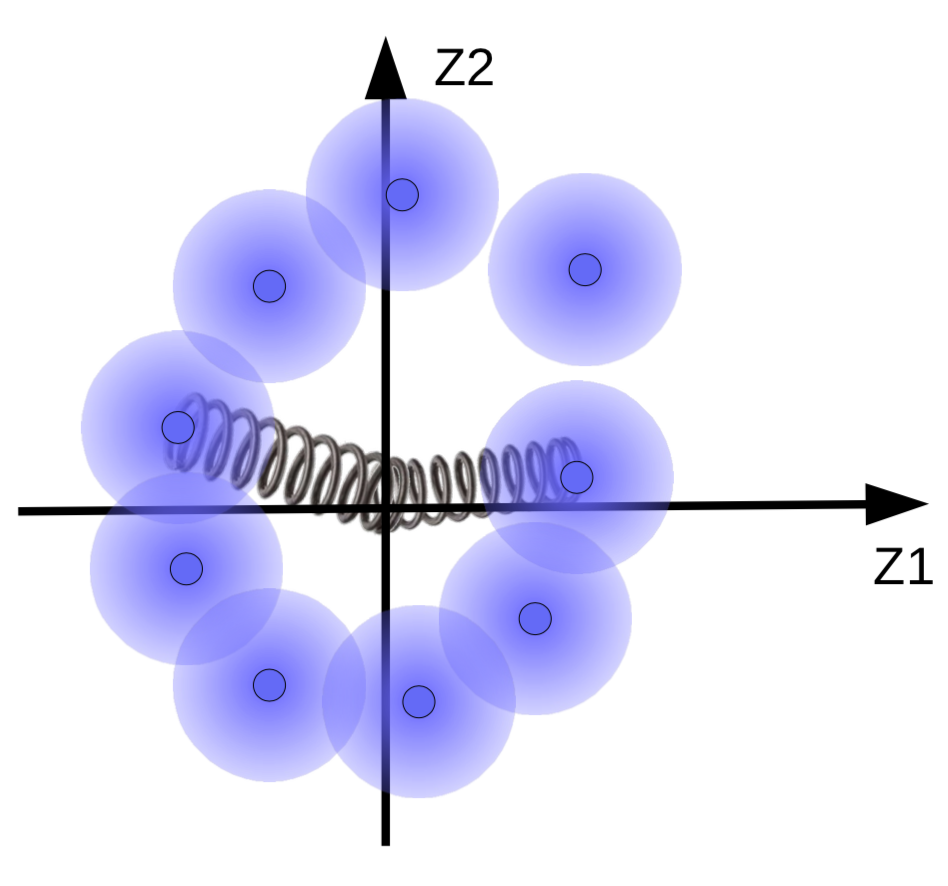
Fig. 10: gli effetti della regolarizzazione visualizzati tramite molle.

La forza della molla determina quanto vicine le sfere sfocate sono all’origine. Se la molla è troppo debole, le sfere si allontanano troppo dall’origine, risultando in alti valori di energia. Per prevenire ciò, il sistema permette alle sfere di sovrapporsi solo se le istanze corrispondenti sono simili.

Non è possibile adattare la dimensione delle sfere sfocate. Essa è limitata da una funzione di penalità (divergenza di Kullback-Leibler) che cerca di rendere la varianza vicina ad 1 così che la dimensione della sfera non sia né troppo grande né troppo piccola da collassare.