Introduzione agli autoencoder

Applicazione degli autoencoder (AE)

Generazione d’immagini

Puoi riconoscere quale fra i volti della Fig. 1 è falso? In effetti, entrambi sono prodotti dal generatore StyleGan2. Nonostante i dettagli facciali siano molto realistici, lo sfondo sembra strano (a sinistra: sfocatura, a destra: oggetti deformati). Questo accade perché la rete neurale è addestrata su campioni di visi. Lo sfondo ha una più grande variabilità. Qui la dimensione della varietà ha circa 50 dimensioni, uguale ai gradi di libertà di un’immagine di un volto.

Fig. 1: volti generati da StyleGan2

Differenze nell’interpolazione nello spazio dei pixel e nello spazio latente

Fig. 2: un cane e un uccello

Se effettuiamo un’interpolazione lineare fra un’immagine di un cane e quella di un unccello (Fig.2) nello spazio dei pixel, otteniamo una sovrapposizione sbiadita delle due immagini, come in Fig. 3. Dall’angolo in alto a sinistra all’angolo in basso a destra, il peso dell’immagine del cane diminuisce, mentre aumenta il peso dell’immagine dell’uccello.

Fig. 3: risultati dopo l'interpolazione

Se si interpola fra due rappresentazioni nello spazio latente e si dà in input il risultato al decoder, si otterrà una trasformazione da cane a uccello come in Fig. 4.

Fig. 4: risultato dopo l'elaborazione del decoder

Ovviamente, lo spazio latente coglie meglio la struttura di un’immagine.

Esempi di trasformazione

Fig. 5: zoom

Fig. 6: traslazione

Fig. 7: luminosità

Fig. 8: rotazione (si noti che la rotazione potrebbe essere in 3D)

Super-risoluzione di immagini

Questo modello punta a miglioirare la risoluzione delle immagini e ricostruire i volti originali. Da sinistra a destra, in Fig. 9, la prima colonna è l’immagine di input (risoluzione 16x16), la seconda è il risultato di una interpolazione bicubica standard, la terza è l’output generato da una rete neurale; a destra vi è l’immagine originaria (https://github.com/david-gpu/srez).

Fig. 9: ricostruzione dei volti originari

Dalle immagini di output è chiaro che vi sono delle distorsioni nei dati di addestramento, il che rende inaccurata la ricostruzione dei volti. Per esempio, l’uomo asiatico in alto a sinistra viene ricostruito, in output, con dei lineamenti europei a causa dello sbilanciamento nelle immagini di addestramento. Il viso ricostruito della donna in basso a sinistra sembra strano a causa della scarsità d’immagini, nei dati di addestramento, da quell’angolatura particolare.

Reintegrazione fotografica

Fig. 10: sovraimposizione di una pezza grigia sui volti

La sovraimposizione di una pezza grigia sui volti, come in Fig. 10, allontana l’immagine dalla varietà di addestramento. La ricostruzione del volto in Fig. 11 è effettuata cercando l’esempio di immagine più vicino giacente nella varietà di addestramento tramite minimizzazione di una funzione di energia.

Fig. 11: ricostruzione dell'immagine di cui alla Fig. 10

Da didascalia a immagine

Fig. 12: esempio di creazione di un'immagine a partire dalla didascalia

La traslazione da descrizione testuale a immagine della Fig. 12 è ottenuta estraendo rappresentazioni di caratteristiche testuali associate a informazioni visive salienti e decodificando queste ultime in immagini.

Cosa sono gli autoencoder

Gli autoencoder sono reti neurali artificiali addestrate in modo non supervisionato, le quali reti puntano prima di tutto a imparare rappresentazioni codificate dei nostri dati, dopodiché a generare nuovamente i dati di input (più accuratamente possibile) dalle rappresentazioni codificate. Quindi, l’output di un autoencoder è una sua previsione dell’input.

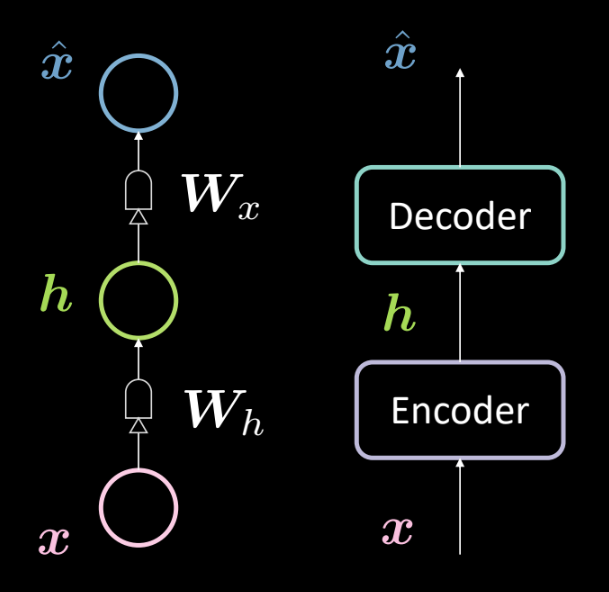
Fig. 13: architettura di un semplice autoencoder

La Fig. 13 mostra l’architettura di un semplice autoencoder. Come prima, iniziamo dal basso con l’input $\boldsymbol{x}$ il quale è soggetto a un codificatore (trasformazione affine definita da $\boldsymbol{W_h}$, seguita da una “spremitura”). Questo risulta in uno strato nascosto intermedio $\boldsymbol{h}$. Questo a sua volta è soggetto a un decodificatore (un’altra trasformazione affine definita da $\boldsymbol{W_x}$ seguita da un’altra “spremitura”). Ciò produce l’output $\boldsymbol{\hat{x}}$, il quale è la previsione/ricostruzione dell’input da parte del modello. Come da nostra convenzione, poniamo che questa sia una rete neurale a 3 strati.

Possiamo rappresentare la rete di cui sopra in maniera matematica utilizzando le seguenti equazioni

Specifichiamo le seguenti dimensionalità:

Nota: affinché possiamo rappresentare le componenti principali (principal component analysis, PCA), dobbiamo porre di avere parametri collegati, ovvero $\boldsymbol{W_x}\ \dot{=}\ \boldsymbol{W_h}^\top$.

Perche utilizziamo gli autoencoder?

A questo punto, ci si potrebbe chiedere quale sia la motivazione di prevedere l’input e quali siano le applicazioni degli autoencoder.

L’applicazione principale di un autoencoder è per il rilevamento di anomalie o la riduzione di rumore (denoising) delle immagini. Sappiamo che il compito di un autoencoder è quello di essere capace di ricostruire i dati giacenti in una varietà, ovvero, data questa varietà, vogliamo che il nostro autoencoder sia capace di ricostruire solo l’input esistente in tale varietà. Quindi limitiamo il modello a ricostruire cose osservate durante l’addestramento, cosicché ogni variazione presente nel nuovo input verrà rimossa in quanto il modello non sarà sensibile a questo tipo di perturbazioni.

Un’altra applicazione di un autoencoder è la compressione d’immagini. Se abbiamo una dimensionalità intermedia $d$ più piccola di quella dell’input $n$, allora il codificatore può essere usato come compressore e le rappresentazioni nascoste (codificate) rappresenterebbero tutta (o quasi tutta) l’informazione dell’input specifico, ma occupando meno spazio.

Errore di ricostruzione

Vediamo ora le funzioni di perdita basate sull’errore di ricostruzione che utilizziamo normalmente. La perdita totale per il dataset è data dalla media della perdita per singola istanza, ovvero

Se l’input è categorico, possiamo usare la perdita basata sull’entropia incrociata (cross-entropy) per calcolare la perdita per istanza, che è data dalla formula

E se l’input assume valori reali, potremmo voler usare la perdita basata sullo scarto quadratico medio, data dalla formula

Strati intermedi sovra-/sottocompleti

Quando la dimensionalità dello strato nascosto $d$ è minore della dimensionalità dell’input $n$, possiamo dire che tale strato nascosto è sottocompleto. Similarmente, quando $d>n$, possiamo chiamarlo uno strato nascosto sovracompleto. La Fig. 14 mostra uno strato nascosto sottocompleto a sinistra e uno sovracompleto a destra.

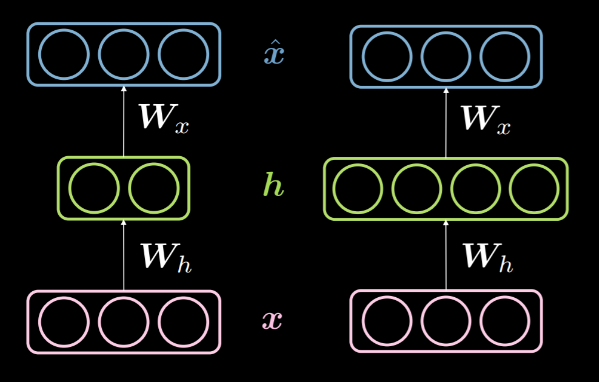
Fig. 14: strati nascosti -- sottocompleto vs. sovracompleto

Come detto sopra, uno strato nascosto sottocompleto può essere usato per fini di compressione, giacché stiamo codificando l’informazione dell’input in meno dimensioni. D’altro canto, in uno strato sovracompleto stiamo codificando in più dimensioni dell’input. Ciò facilita l’ottimizzazione.

Siccome stiamo cercando di ricostruire l’input, il modello è propenso a copiare tutte le caratteristiche dell’input nello strato nascosto, cercando di farlo passare all’output, essenzialmente comportandosi come la funzione identità. Ciò va necessariamente evitato in quanto implicherebbe che il nostro modello fallisce nell’apprendimento. Dunque, dobbiamo applicare qualche vincolo ulteriore applicando un collo di bottiglia dell’informazione. Lo facciamo per limitare le possibili configurazioni che lo strato nascosto può assumere a solo quelle configurazioni viste durante l’addestramento. Ciò permette una ricostruzione selettiva (limitata ad un sottoinsieme dello spazio d’input) e rende il modello insensibile a qualsiasi cosa non presente nella varietà.

C’è da notare che uno strato sottocompleto non può comportarsi come la funzione identità samplicemente perché esso non ha abbastanza dimensioni per copiare l’input. Quindi, uno strato nascosto sottocompleto è meno incline a sovradattare se comparato con uno strato sovracompleto, ma potrebbe sempre farlo. Per esempio, dati un codificatore e un decodificatore potenti, il modello potrebbe semplicemente associare un numero a ogni dato e imparare la mappatura. Ci sono svariati metodi per evitare il sovradattamento come metodi di regolarizzazione, architettonici, ecc.

Autoencoder per la riduzione del rumore (denoising autoencoder)

La Fig. 15 mostra la varietà dell’autoencoder per la riduzione del rumore e l’intuizione sul suo funzionamento.

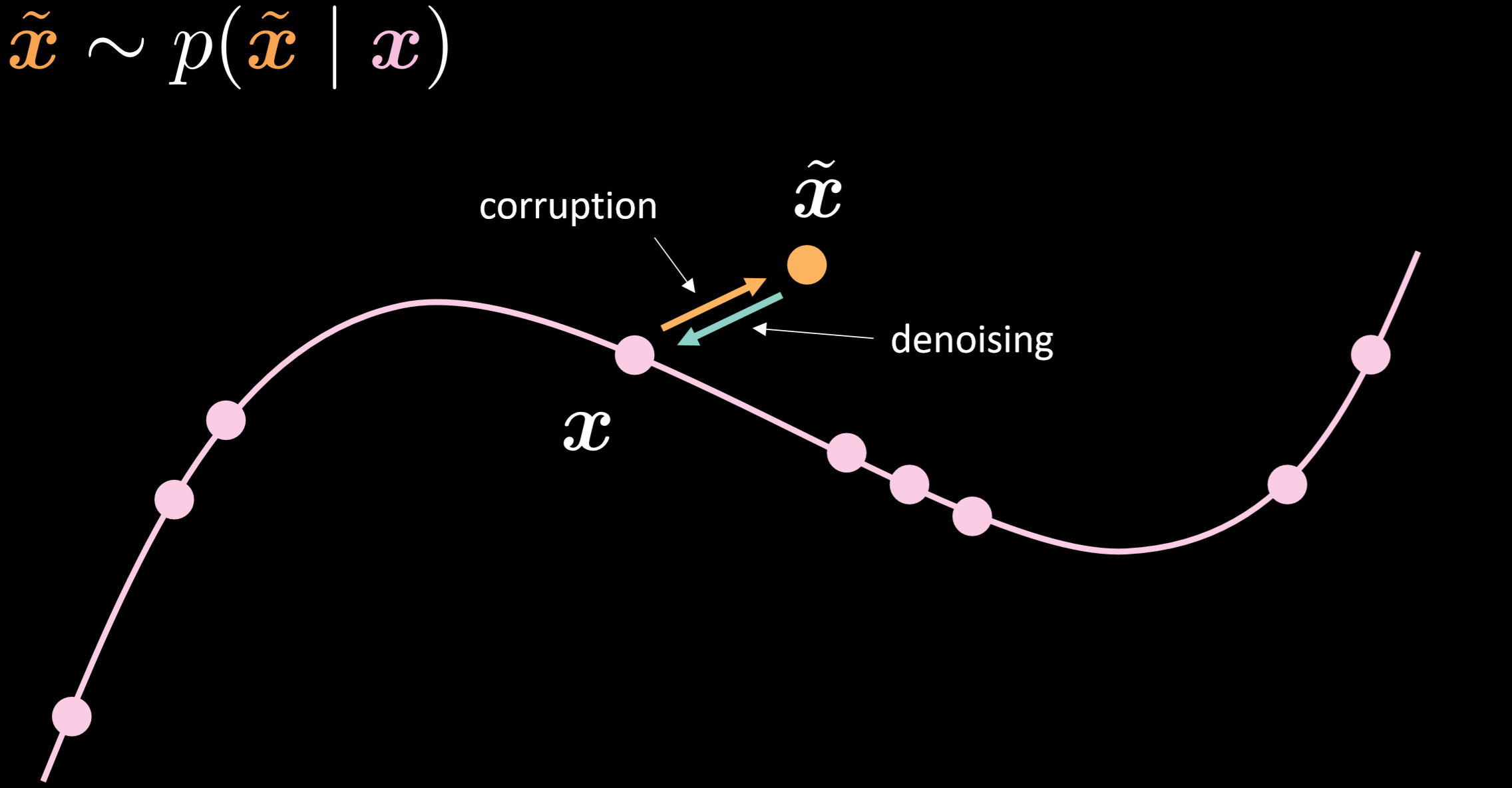
Fig. 15: autoencoder per la riduzione del rumore

In questo modello, assumiamo di voler iniettare la stessa distribuzione rumorosa che osserviamo nella realtà, così che possiamo imparare come poterla recuperare robustamente. Comparando l’input e l’output, possiamo vedere che i dati già presenti nella varietà non si sono mossi, mentre quelli che ne erano lontani si sono mossi di molto.

La Fig. 16 ci dà la relazione fra dati d’input e di output.

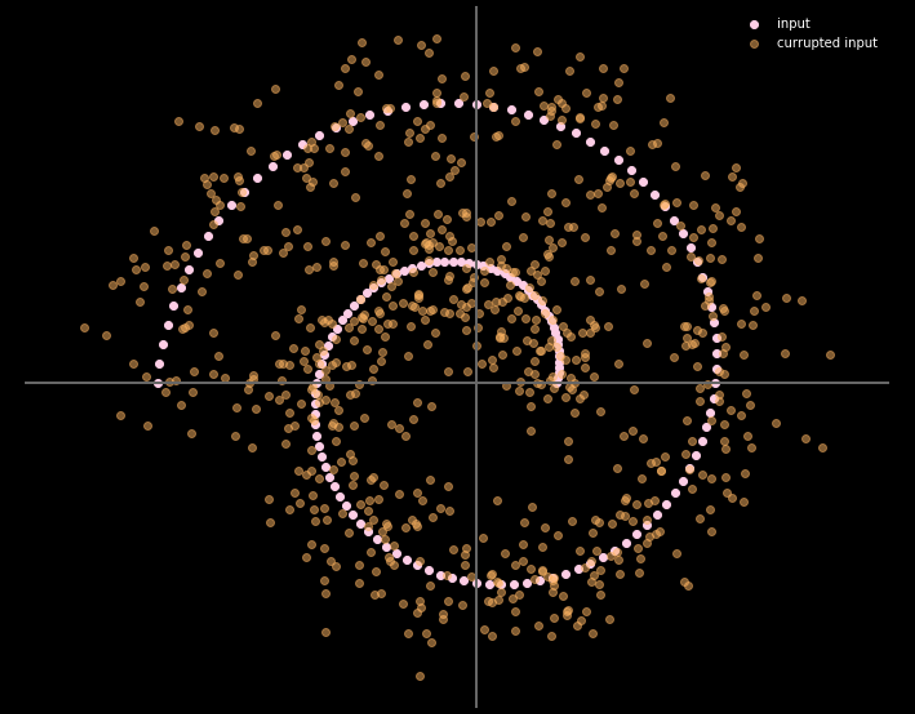
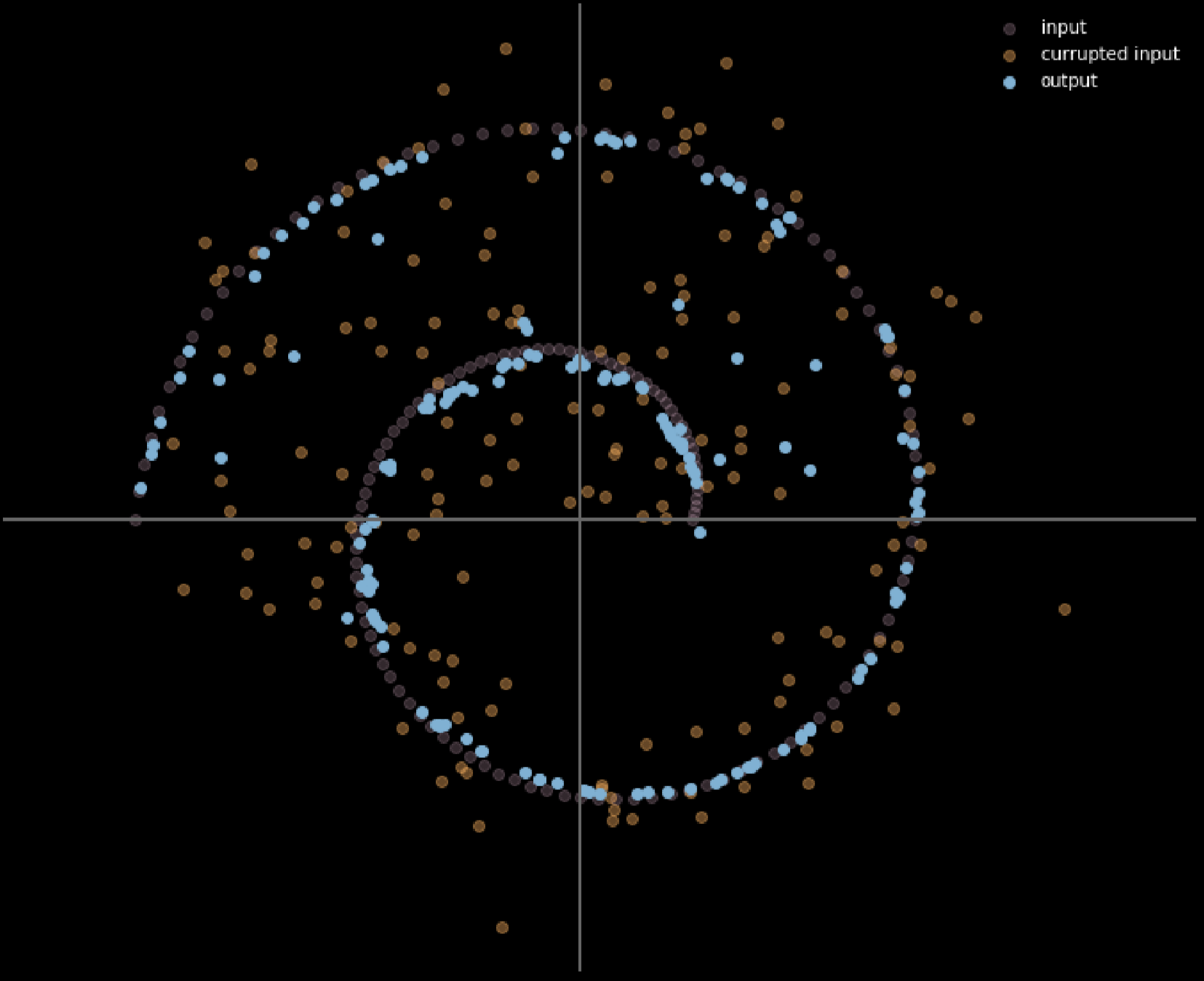
Fig. 16: input e output dell'autoencoder per la riduzione del rumore

Possiamo anche utilizzare colori differenti per rappresentare la distanza della quale ogni punto si è mosso; la Fig. 17 ne mostra il diagramma.

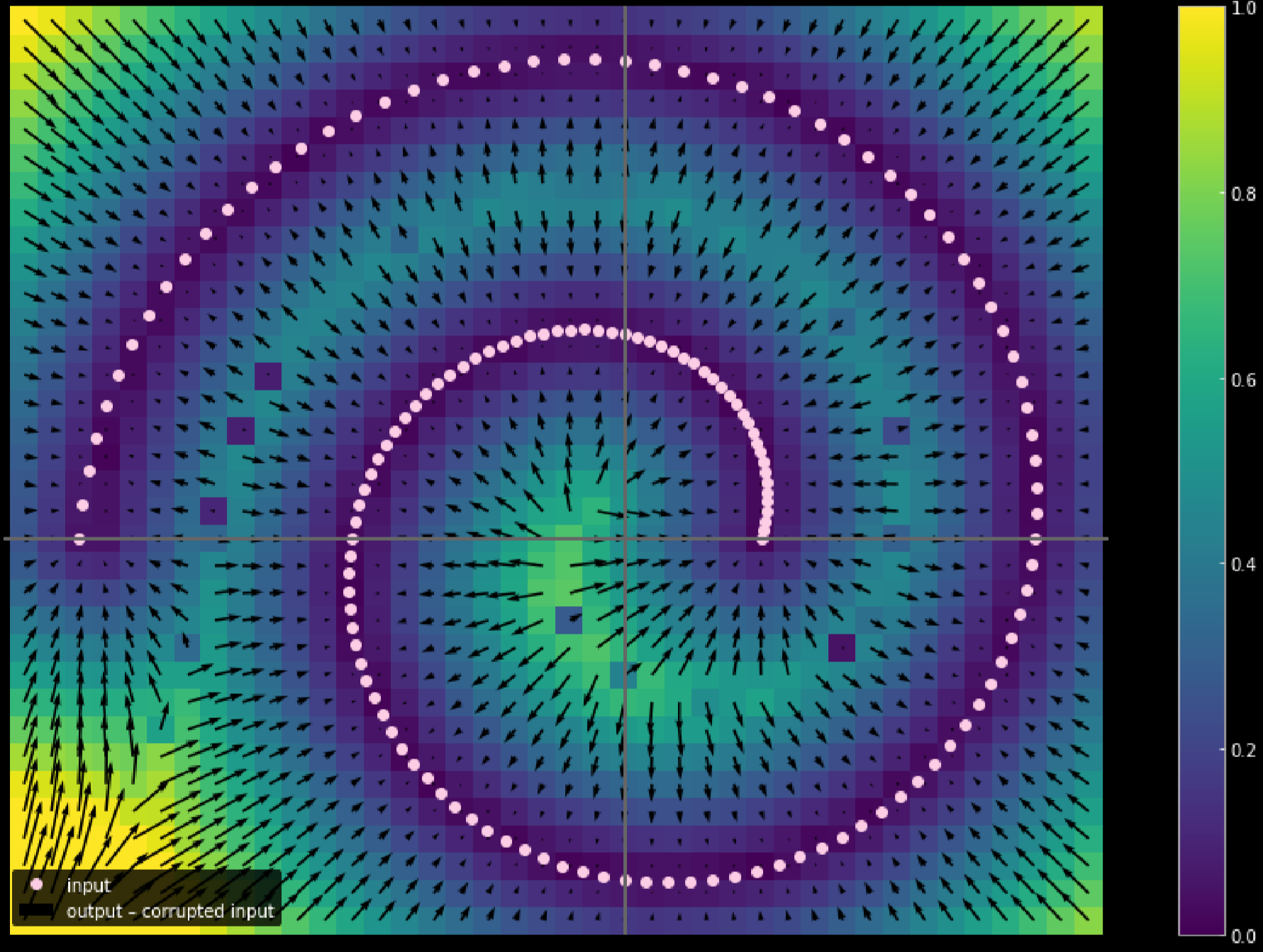
Fig. 17: misurare la distanza percorsa da ogni dato d'input

Più chiaro è il colore, più grande è la distanza percorsa dal punto. Dal diagramma, si può notare che i punti agli angoli hanno percorso una distanza vicina a 1 unità, mentre i punti all’interno dei 2 rami non si sono mossi per nulla, in quanto sono attratti dai rami in alto e in basso durante il processo di addestramento.

Autoencoder contrattivi

La Fig. 18 mostra la funzione di perdita e la varietà dell’autoencoder contrattivo

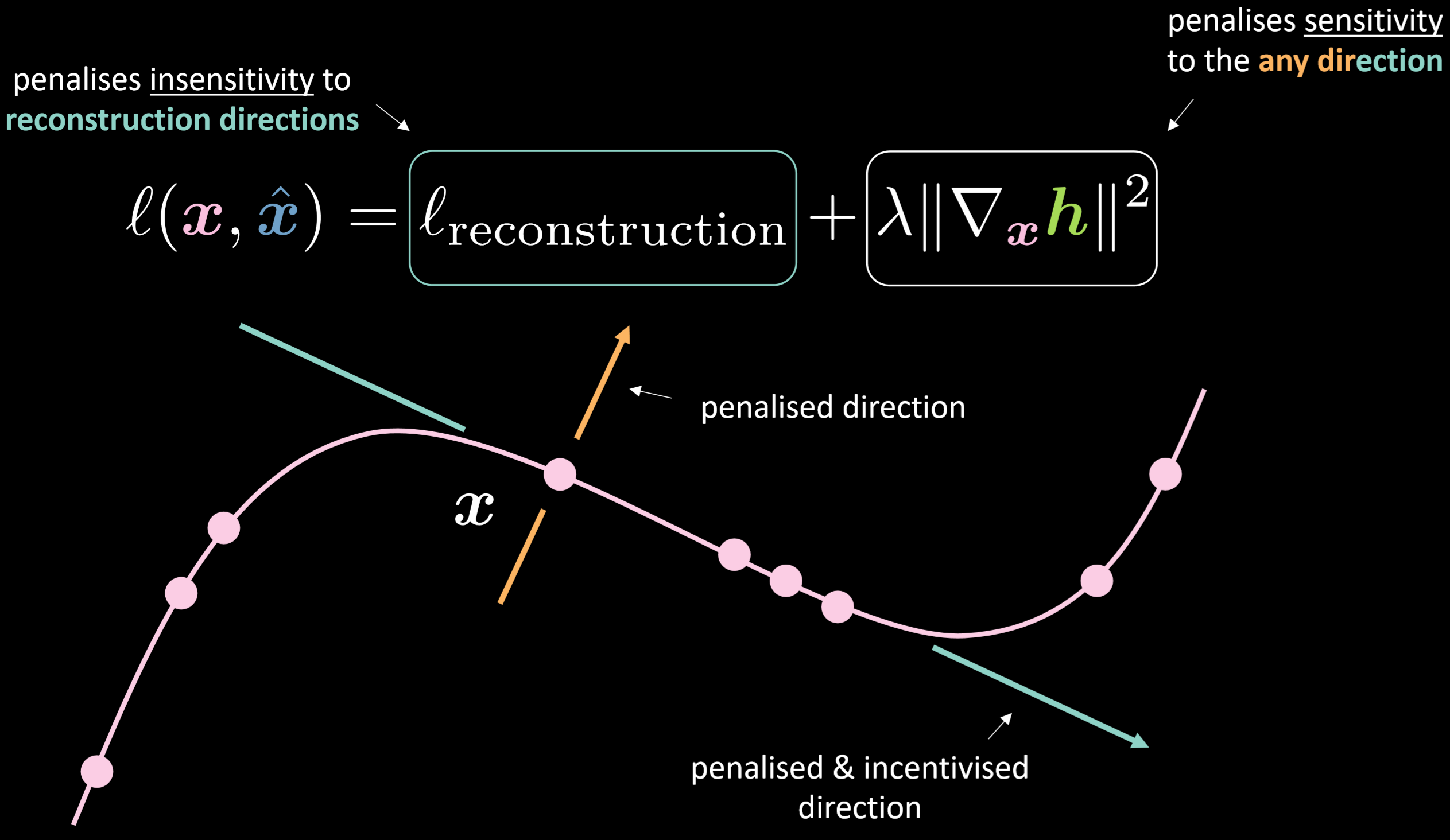
Fig. 18: autoencoder contrattivo

La funzione di perdita contiene il termine di ricostruzione più la norma al quadrato del gradiente della rapppresentazione nascosta sull’input. Quindi, la perdita complessiva minimizza la variazione dello strato nascosto data una variazione dell’input. Il beneficio è quello di rendere il modello sensibile alle direzioni di ricostruzione e insensibile a tutte le altre direzioni.

La Fig. 19 mostra come questi autoencoder funzionano in generale.

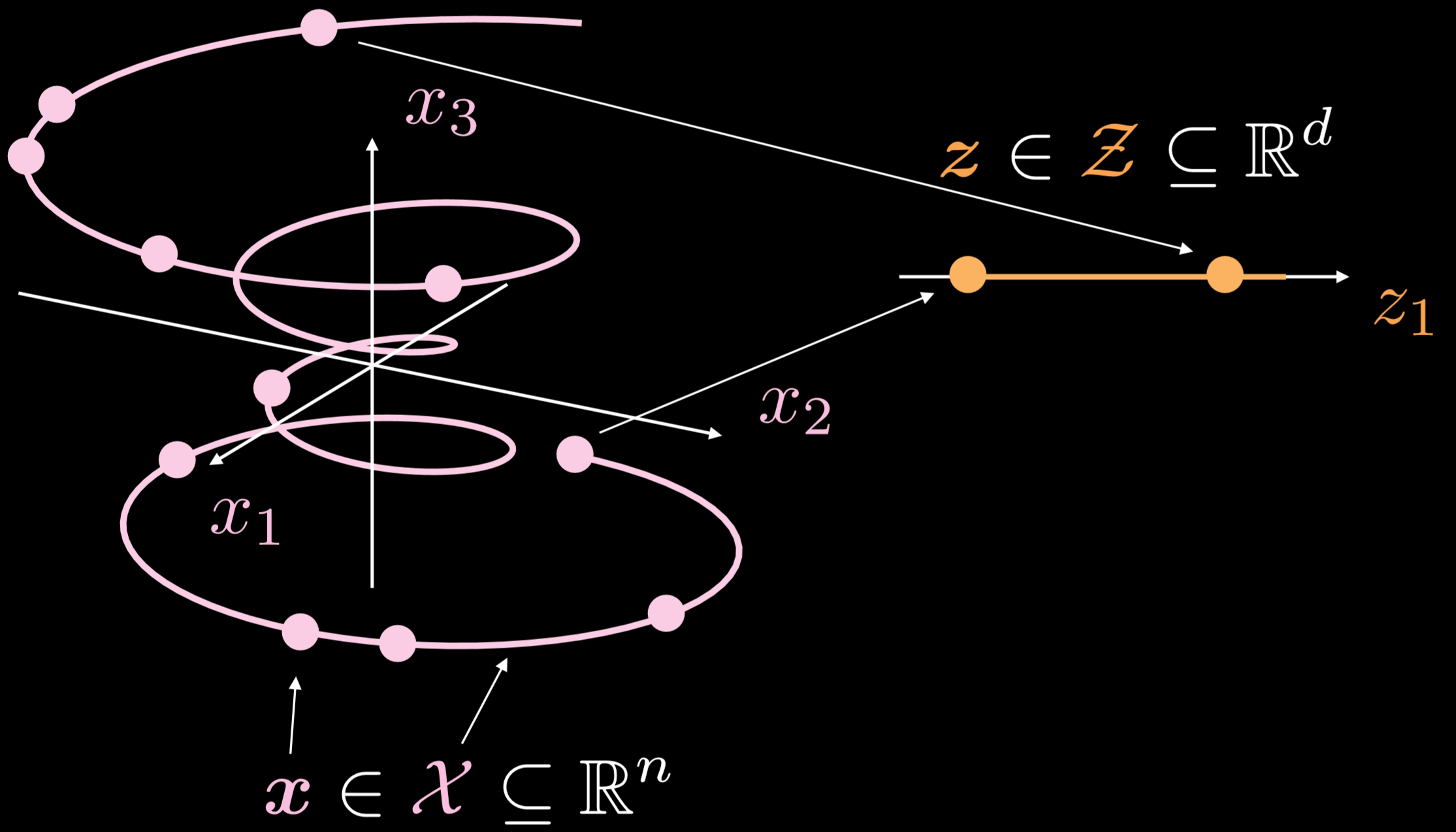
Fig. 19: autoencoder basilare

La varietà di addestramento è un oggetto unidimensionale che si muove in tre dimensioni. Dato $\boldsymbol{x}\in \boldsymbol{X}\subseteq\mathbb{R}^{n}$, l’obiettivo dell’autoencoder è di distendere lungo una direzione la linea “arricciata”, dove $\boldsymbol{z}\in \boldsymbol{Z}\subseteq\mathbb{R}^{d}$. Il risultato di ciò è che un punto dell’input sarà trasformato in un punto dello spazio latente. Ora abbiamo la corrispondenza tra punti dell’input e punti nello spazio latente, ma non abbiamo la corrispondenza fra regioni dello spazio d’input e regioni dello spazio latente. Successivamente, utilizzeremo il decodificatore per trasformare un punto dello strato latente per generare uno strato di output che abbia significato.

Implementazione degli autoencoder - Notebook

Il Jupyter Notebook può essere reperito qui.

In questo notebook, implementeremo un autoencoder standard ed un autoencoder per la riduzione del rumore e ne compareremo gli output.

Definizione dell’architettura dell’autoencoder e la perdita di ricostruzione

Abbiamo immagini di dimensione $28 \times 28$ e usiamo uno strato nascosto di dimensione $30$. La routine di trasformazione tratta in questo modo le dimensioni: $784\to30\to784$. Applicando la funzione tangente iperbolica alle routine di codificazione e decodificazione, siamo in grado di limitare il range dell’output nell’intervallo $(-1,1)$. Lo scarto quadratico medio (mean squared error, MSE) verrà usato come funzione di perdita del modello.

python=
class Autoencoder(nn.Module):
    def __init__(self):
        super().__init__()
        self.encoder = nn.Sequential(
            nn.Linear(n, d),
            nn.Tanh(),
        )
        self.decoder = nn.Sequential(
            nn.Linear(d, n),
            nn.Tanh(),
        )

    def forward(self, x):
        x = self.encoder(x)
        x = self.decoder(x)
        return x

model = Autoencoder().to(device)
criterion = nn.MSELoss()

Addestramento di un autoencoder standard

Per addestrare un autoencoder standard usando PyTorch, bisogna inserire questi 5 metodi nel ciclo di addestramento:

Passaggio in avanti:

1) Passaggio dell’immagine d’input attraverso il modello chiamando output = model(img).
2) Calcolo della perdita tramite criterion(output, img.data).

Passaggio all’indietro:

3) Azzerare il gradiente per assicurarci di non accumularne il valore: optimizer.zero_grad().
4) Retropropagazione: loss.backward()
5) Passo all’indietro: optimizer.step()

La Fig. 20 mostra l’output di un autoencoder standard.

Fig. 20: output di un autoencoder standard

Addestrare un autoencoder per la riduzione del rumore

Per l’autoencoder per la riduzione del rumore, bisogna aggiungere i seguenti passaggi: 1) Chiamare nn.Dropout() per “spegnere” in maniera casuale alcuni neuroni.
2) Creare la maschera per il rumore: do(torch.ones(img.shape)).
3) Creare immagini perturbate (“cattive”) moltiplicando le immagini reali (“buone”) con la maschera binaria: img_bad = (img * noise).to(device)

La Fig. 21 mostra l’output dell’autoencoder per la riduzione del rumore.

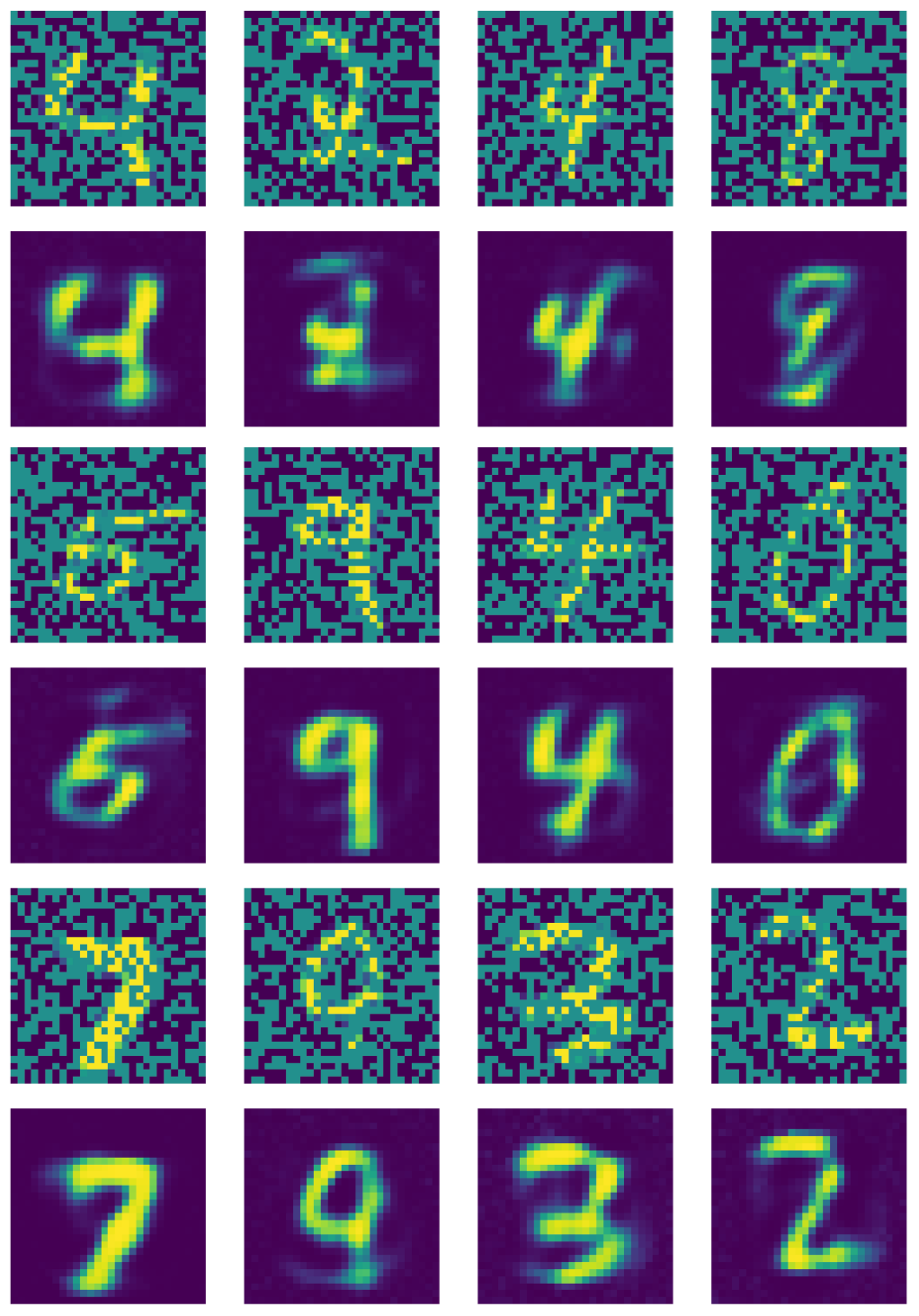
Fig.21: output dell'_autoencoder_ per la riduzione del rumore

Comparazione dei filtri

È importante notare che, nonostante il fatto che le dimensioni dello strato di input siano $28 \times 28 = 784$, uno strato nascosto con dimensione pari a $500$ sia comunque ancora uno strato sovracompleto a causa del numero di pixel neri nell’immagine. Di sotto vi sono esempi di filtri utilizzati in un autoencoder standard sottocompleto addestrato. Chiaramente, i pixel nella regione dove esistono i numeri indicano il riconoscimento di una qualche sorta di pattern, mentre i pixel al di fuori di questa regione sono pressoché casuali. Ciò indica che l’autoencoder standard non s’interessa dei pixel fuori dalla regione dove si trova il numero.

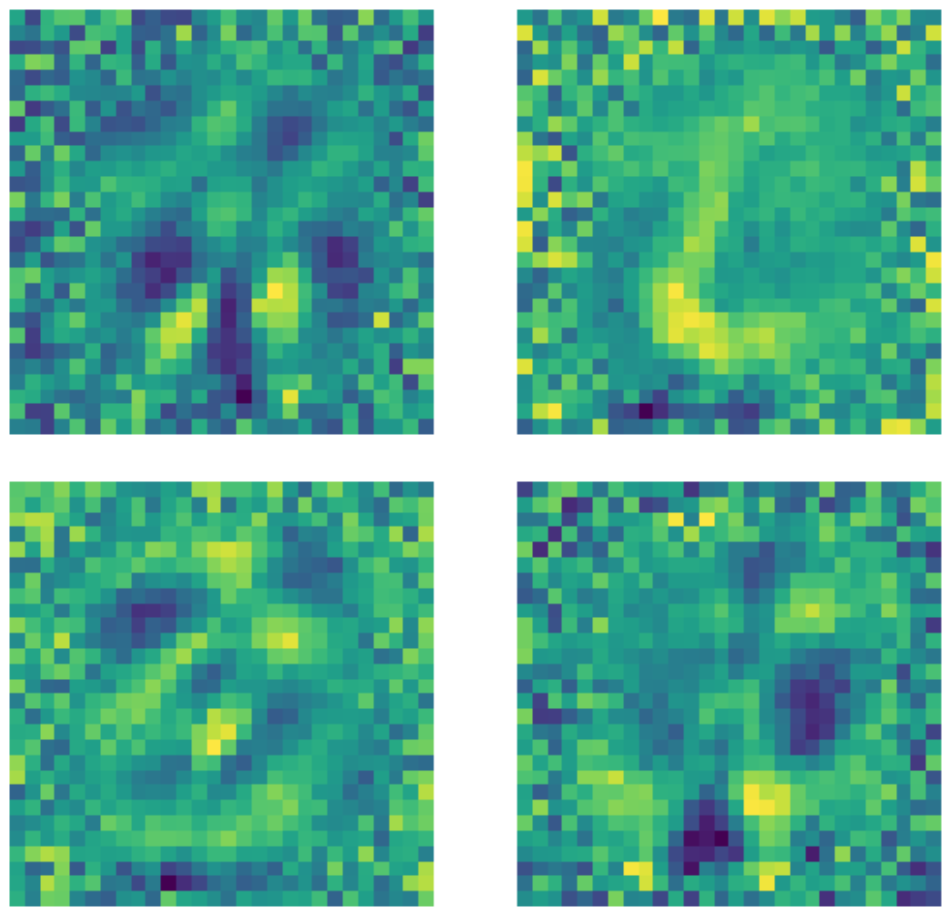
Fig. 22: filtri di un AE standard.

D’altro canto, quando lo stesso dato viene dato in pasto ad un autoencoder per la riduzione del rumore con una maschera di dropout applicata ad ogni immagine prima di applicarvi il modello, si verifica qualcosa di diverso. Ogni filtro che impara un pattern, impara anche ad assegnare un valore costante ai pixel esterni alla regione dove si trova il numero.

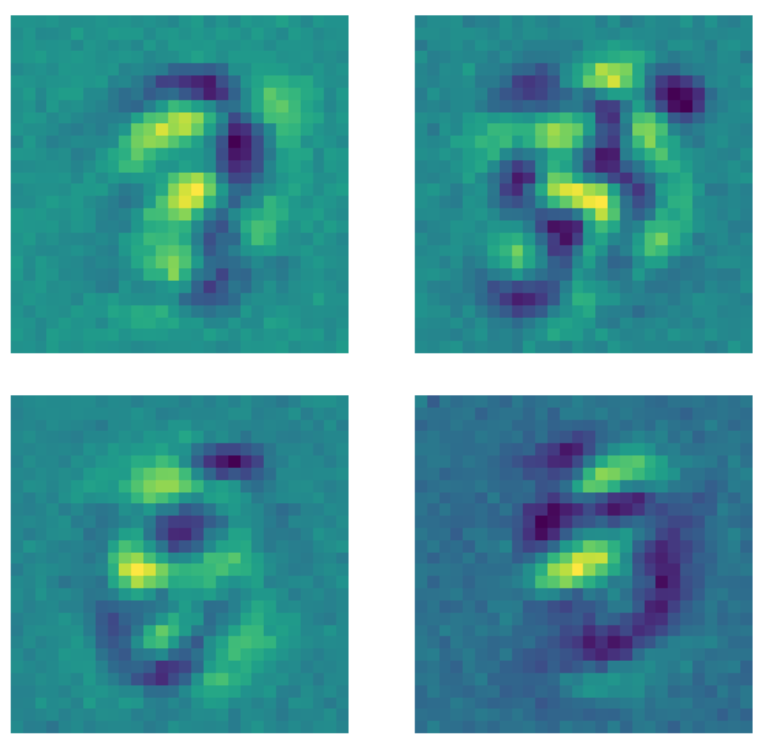
Fig. 23: filtri di un AE per la riduzione del rumore

Se comparato allo stato dell’arte, il nostro autoencoder si comporta persino meglio! Si può notare ciò dai risultati esposti sotto.

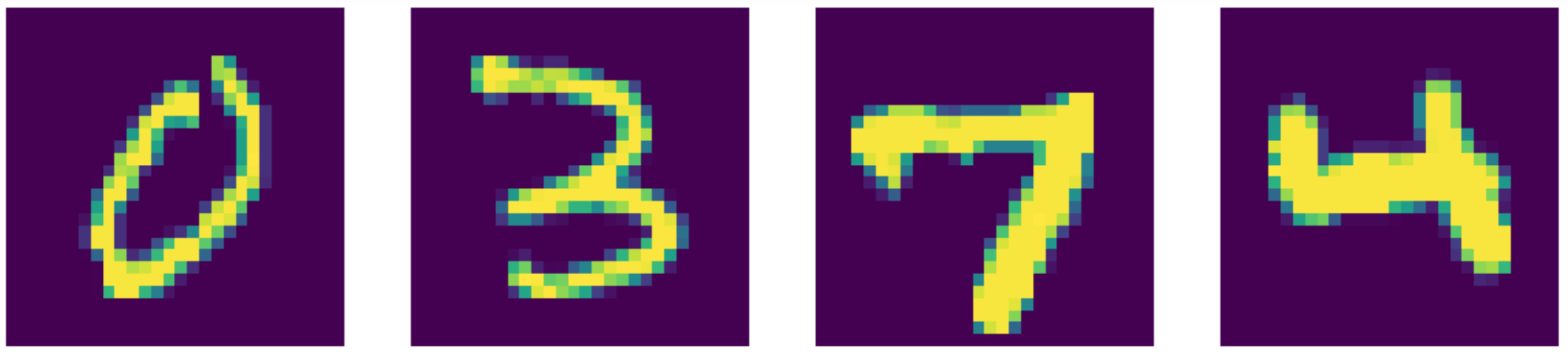
Fig. 24: dati di input (cifre da MNIST).

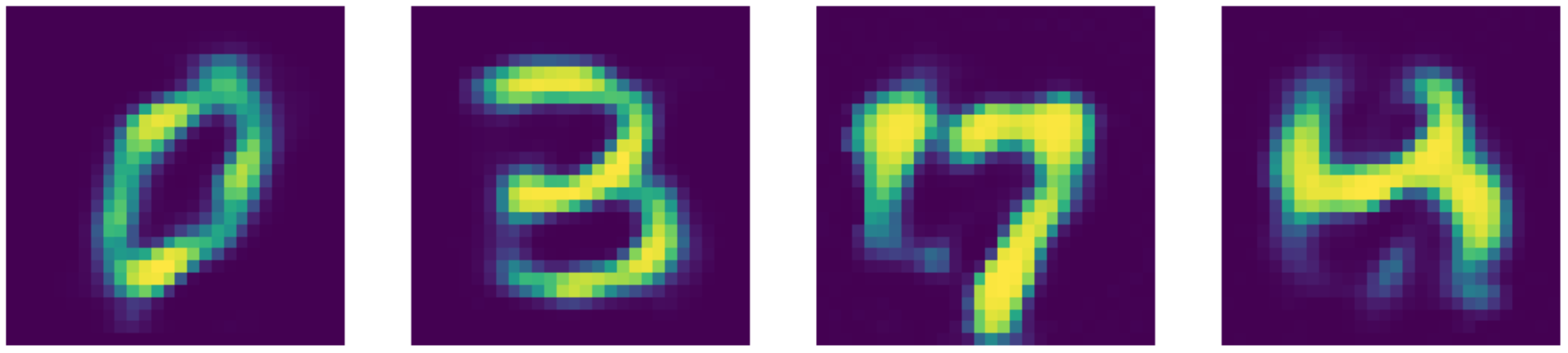
Fig. 25: ricostruzioni dell'autoencoder per la riduzione del rumore

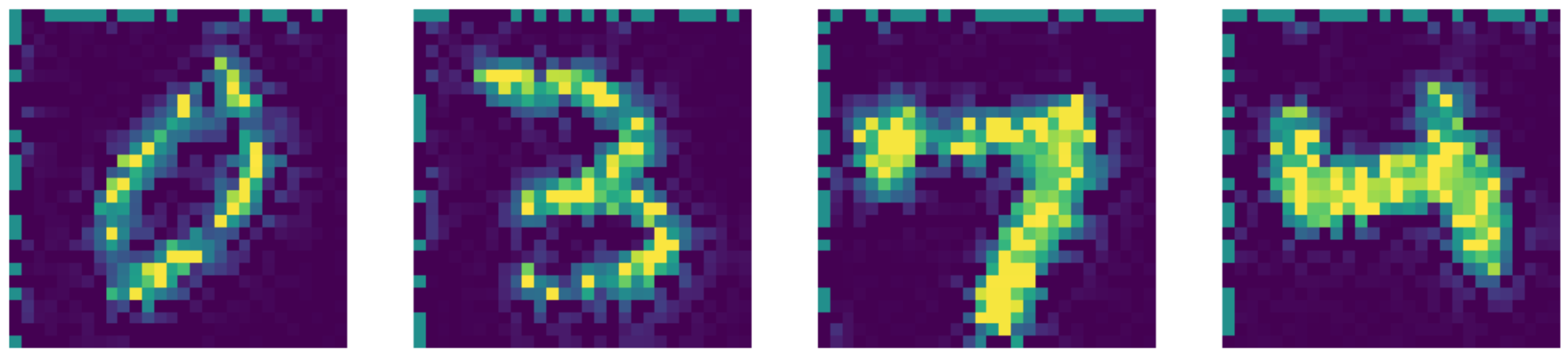
Fig. 26: output dell'inpainting di Telea.

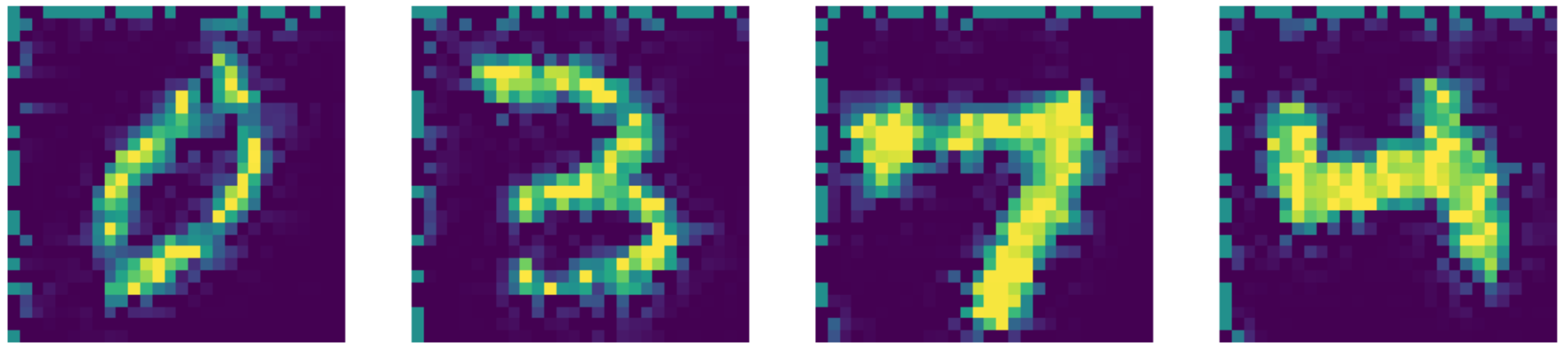
Fig. 27: output dell'inpainting di Navier-Stokes.