SSL, EBM con dettagli ed esempi

Apprendimento auto-supervisionato

L’apprendimento auto-supervisionato (self-supervised learning, SSL) abbraccia sia l’apprendimento supervisionato che quello non supervisionato. Il pretesto dell’SSL è quello di imparare una buona rappresentazione dell’input che può conseguentemente essere utilizzata per compiti supervisionati. Nell’SSL, il modello è addestrato a prevedere una parte dei dati condizionatamente al fatto di conoscere un’altra parte degli stessi. Per esempio, BERT è stato addestrato usando tecniche di SSL e l’autoencoder per denoising, in particolare, ha prodotto risultati allo stato dell’arte per quanto riguarda il processamento del linguaggio naturale (NLP).

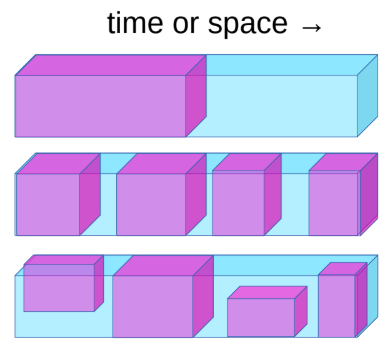
Fig. 1: apprendimento auto-supervisionato (*Self Supervised Learning*)

I compiti di apprendimento auto-supervisionato possono essere definiti come:

• prevedere il futuro a partire dal passato;
• prevedere ciò che è occluso a partire da ciò che è visibile.

Per esempio, se un sistema è addestrato a prevedere il prossimo frame quanto la telecamera si sta muovendo, il sistema imparerà in maniera implicita la profondità e la parallasse. Questo forzerà il sistema ad imparare che gli oggetti occlusi dalla sua visione non spariscono, ma continuano ad esistere; inoltre, imparerà la distinzione fra oggetti animati, inanimati e lo sfondo. Può anche finire per imparare concetti intuitivi di fisica come la gravità.

I sistemi di NLP allo stato dell’arte come BERT pre-addestrano una gigantesca rete neurale sulla base di compiti di SSL. Si rimuovono delle parole da una frase e si richiede al sistema di predire le parole mancanti. Ciò è risultato dare risultati di ampio successo. Idee simili erano anche state provate nel mondo della visione artificiale. Come mostrato nell’immagine sotto, si possono prendere delle immagini e rimuovere una porzione di figura, addestrando il modello a prevedere la porzione mancante.

Fig. 2: risultati analoghi nella visione artificiale

Nonostante questi modelli possano completare gli spazi vuoti mancanti, essi non hanno ottenuto lo stesso successo dei sistemi di NLP. Se si dovesse considerare una rappresentazione interna generata da questi modelli come input di un sistema di visione artificiale, sarebbe impossibile battere un modello pre-addestrato in maniera supervisionata su ImageNet. La differenza qui è che l’NLP lavora in un dominio discreto, mentre le immagini sono continue. Il divario per quanto concerne il successo è dovuto al fatto che in un dominio discreto sappiamo come rappresentare l’incertezza: possiamo utilizzare un softmax (esponenziale normalizzata) sui possibili output, mentre nel continuo non siamo in grado di farlo.

Un sistema intelligente (agente d’intelligenza artificiale) dev’essere in grado di predire i risultati delle sue stesse azioni prese sui suoi dintorni e su se stesso, al fine di prendere decisioni intelligenti. Siccome il mondo non è completamente deterministico e una macchina o un cervello umano non hanno abbastanza potenza di calcolo per considerare tutte le possibilità, dobbiamo insegnare ai sistemi AI (artificial intelligence) di effettuare le previsioni in presenza di incertezza in spazi di grandi dimensioni. I modelli basati sull’energia (energy based models, EBM) possono essere estremamente utili a riguardo.

Una rete neurale addestrata usando i minimi quadrati per predire il prossimo frame di un video risulterà in immagini sfocate perché il modello non può predire esattamente il futuro, così impara, dai dati di addestramento, a fare la media di tutte le possibilità per il prossimo frame al fine di ridurre la perdita.

I modelli a variabile latente basati sull’energia come soluzione per predire il prossimo frame

A differenza della regressione lineare, i modelli a variabile latente basati sull’energia considerano ciò che conosciamo del mondo, più una variabile latente che ci dà informazioni riguardo a cosa è accaduto nella realtà. Una combinazione di queste due informazioni può essere usata per effettuare una previsione vicina a quanto accadrà.

Si può pensare a questi modelli come dei sistemi che valutano la compatibilità fra l’input $x$ e l’output effettivo $y$ in base alla previsione, effettuata utilizzando la variabile latente, minimizzante l’energia del sistema. Si osserva l’input $x$ e si produce una possibile previsione $\bar{y}$ per diverse combinazioni dell’input $x$ e delle variabili latenti $z$ e si sceglie quella che minimizza l’energia, ovvero l’errore di previsione, del sistema.

Dipendentemente dalla variabile latente che scegliamo, possiamo ottenere tutte le possibili previsioni. La variabile latente può essere pensata come un’informazione importante di $y$ che non è presente nell’input $x$.

Le funzioni di energia a valori scalari possono essere di due tipi:

1. $F(x, y)$ condizionate - misurano la compatibilità fra $x$ e $y$
2. $F(y)$ incondizionate - misurano la compatibilità fra le componenti di $y$

Addestrare un modello basato sull’energia

Ci sono due classi di modelli di apprendimento per addestrare i modelli basati sull’energia ai fini di parametrizzare $F(x,y)$:

1. Metodi contrastivi: far decrescere $F(x[i], y[i])$, far aumentare altri punti $F(x[i], y’)$
2. Metodi architettonici: costruire $F(x,y)$ così che il volume delle regioni a bassa energia è limitato o minimizzato tramite tecniche di regolarizzazione

Ci sono sette strategie per dar forma alle funzioni di energia. I metodi contrastivi differiscono nel modo in cui selezionano i punti per causare l’aumento, mentre i metodi architettonici differiscono nelle tecniche tramite le quali limitano la capacità d’informazione del codice.

Un esempio di metodo contrastivo è l’apprendimento basato su massima verosimiglianza. L’energia può essere interpretata come una densità di probabilità logaritmica, negativa, non normalizzata. La distribuzione di Gibbs ci fornisce la verosimiglianza di $y$ dato $x$. Può essere formulata come di seguito:

La massima verosimiglianza cerca di rendere il numeratore grande e il denominatore piccolo ai fini della massimizzazione. Ciò equivale a minimizzare $-\log(P(Y \mid W))$, ovvero

Gradient of the negative log likelihoood loss for one sample Y is as follows:

Nel gradiente qui sopra, il primo termine del gradiente al punto $Y$ e il secondo termine del gradiente ci forniscono il valore atteso del gradiente dell’energia su tutti i $Y$.

Quindi, quando operiamo una discesa del gradiente, il primo termine prova a ridurre l’energia fornita dal punto $Y$ e il secondo termine prova ad aumentare l’energia data a tutti gli altri $Y$.

Il gradiente della funzione di energia è usualmente molto complesso e quindi la computazione, la stima o l’approssimazione del suo integrale è un caso molto interessante in quanto è intrattabile nella maggior parte dei casi.

Modelli a variabile latente basati sull’energia

Il vantaggio principale dei modelli a variabile latente è che permettono di effettuare previsioni plurime attraverso la variabile latente. Al variare di $z$ in un insieme definito, $y$ muta all’interno della varietà delle possibili previsioni. Alcuni esempi sono:

1. K-means
2. Modellazione sparsa
3. Ottimizazione generativa a variabile latente Generative Latent Optimization (GLO)

Questi modelli possono essere di due tipi:

1. Modelli condizionati in cui $y$ dipende da $x$
   1. \[F(x,y) = \text{min}_{z} E(x,y,z)\]
   2. \[F_\beta(x,y) = -\frac{1}{\beta}\log\int_z e^{-\beta E(x,y,z)}\]
2. Modelli incondizionati con funzioni di energia a valori scalari, in cui $F(y)$ misura la compatibilità fra le componenti di $y$
   1. \[F(y) = \text{min}_{z} E(y,z)\]
   2. \[F_\beta(y) = -\frac{1}{\beta}\log\int_z e^{-\beta E(y,z)}\]

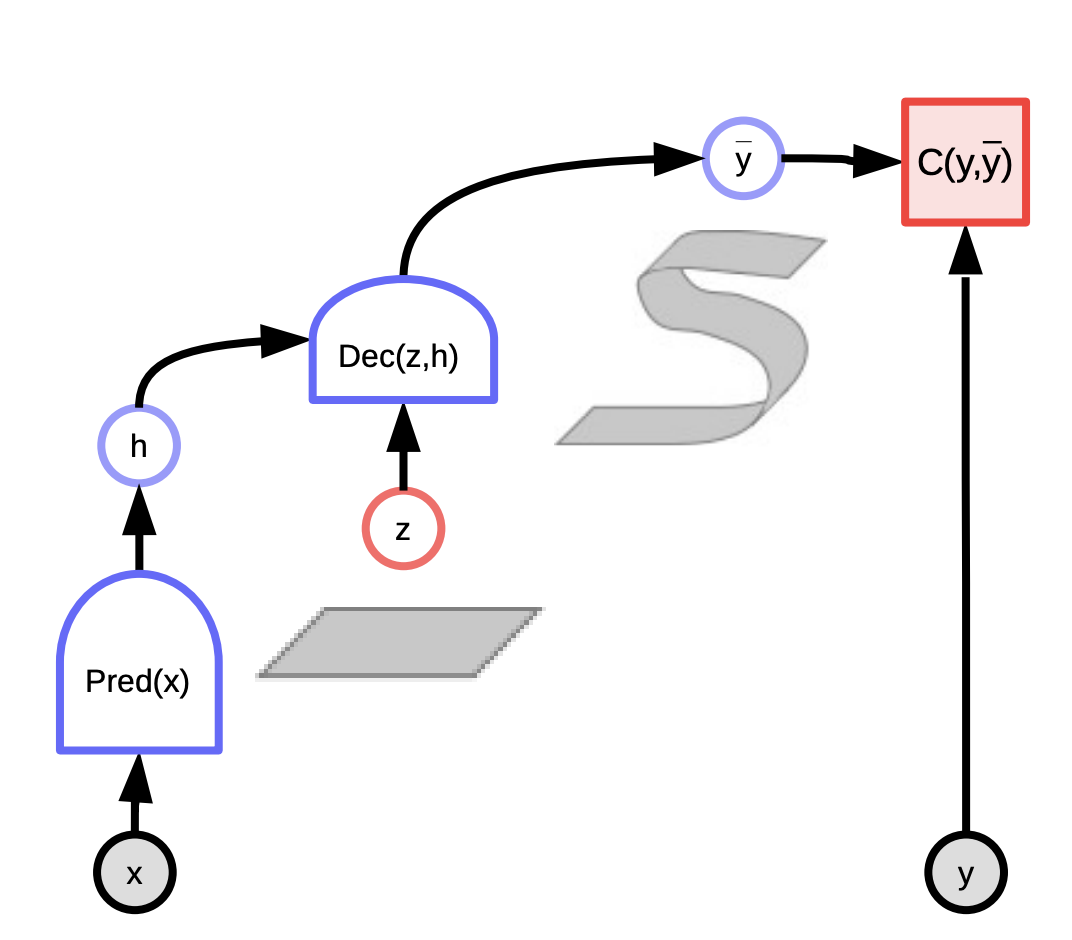
Fig. 3: EBM a variabile latente

Esempio di EBM a variabile latente: K-means

L’algoritmo K-means è un metodo di clustering partizionale il quale può anche essere considerato un modello basato sull’energia nel quale stiamo cercando di modellare una distribuzione su $y$. La funzione di energia è $E(y,z) = \Vert y-Wz \Vert^2$, dove $z$ è un vettore one-hot ($0$ ovunque tranne per un elemento valorizzato a $1$).

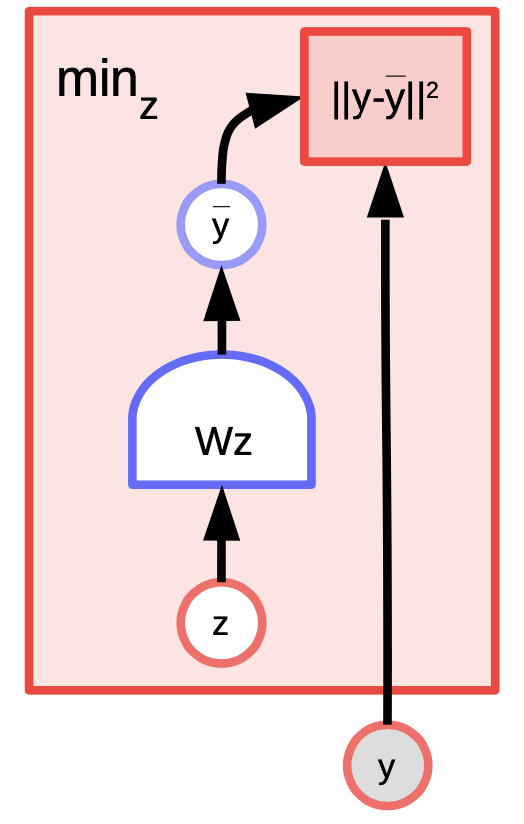
Fig. 4: esempio di K-means

Dati i valori di $y$ e $k$, possiamo fare inferenza ottenendo quale delle $k$ possibili colonne di $W$ minimizzi l’errore di ricostruzione o la funzione di energia. Per addestrare l’algoritmo, possiamo adottare un approccio dove dobbiamo trovare uno $z$ in modo tale da scegliere le colonne di $W$ più vicine a $y$ e cercare di avvicinarcisi sempre di più prendendo un passo del gradiente e ripetendo il procedimento. Tuttavia, il coordinate descent funziona meglio e più velocemente.

Nel grafico sotto possiamo vedere i punti lungo la spirale rosa. Le chiazze nere attorno alla linea corrispondono ad avvallamenti quadratici attorno a ogni prototipo di $W$.

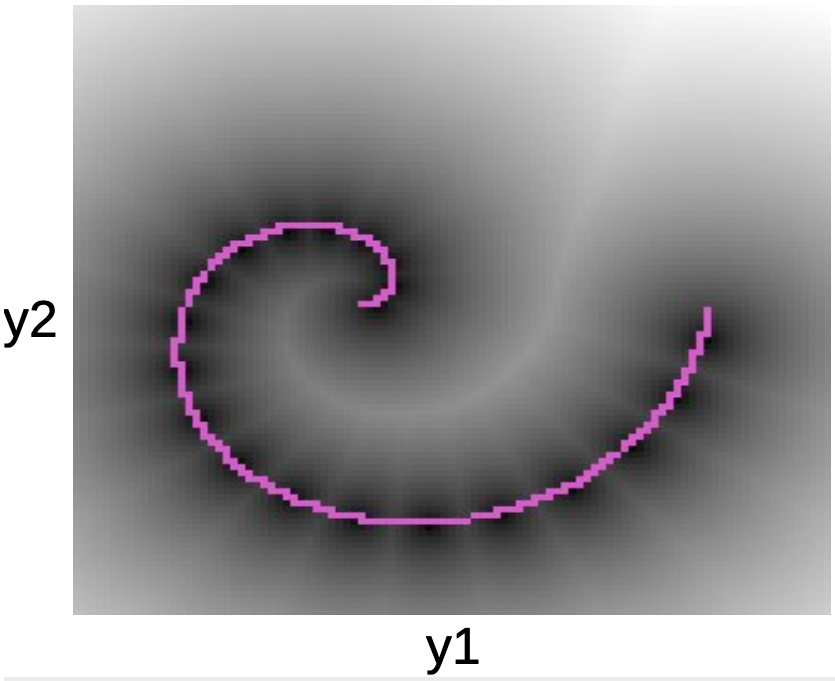
Fig. 5: grafico della spirale

Una volta che abbiamo imparato la funzione di energia, possiamo chiederci domande come:

1. Dato un punto $y_1$, come possiamo prevedere $y_2$?
2. Dato $y$, possiamo trovarne il punto più vicino nella varietà dei dati?

K-means appartiene ai metodi architettonici (opposti ai metodi contrastivi). Di conseguenza, piuttosto che aumentare l’energia, riduciamo l’energia per alcune regioni. Uno svantaggio di ciò è che una volta che il valore di $k$ è stato scelto, ci possono essere solo $k$ punti che hanno energia $0$ e tutti gli altri punti avranno un livello di energia crescente in maniera quadratica come ci allontaniamo da questi punti.

Metodi contrastivi

Secondo il Dr. Yann LeCun, tutti useranno metodi architettonici ad un certo punto nel futuro, ma, in questo momenti, sono i metodi contrastivi a funzionare bene sulle immagini. Si consideri la figura di sotto che ci mostra alcuni punti e curve di livello della superficie dell’energia. Idealmente, desidereremmo che la superficie abbia l’energia più bassa nella varietà dei dati. Di conseguenza, vorremmo abbassare l’energia (ovvero il valore di $F(x,y)$) attorno agli esempi di addestramento, ma ciò potrebbe non bastare. Quindi aumentiamo l’energia per le $y$ nella regione laddove esse avrebbero dovuto avere alta energia, ma ce l’hanno bassa.

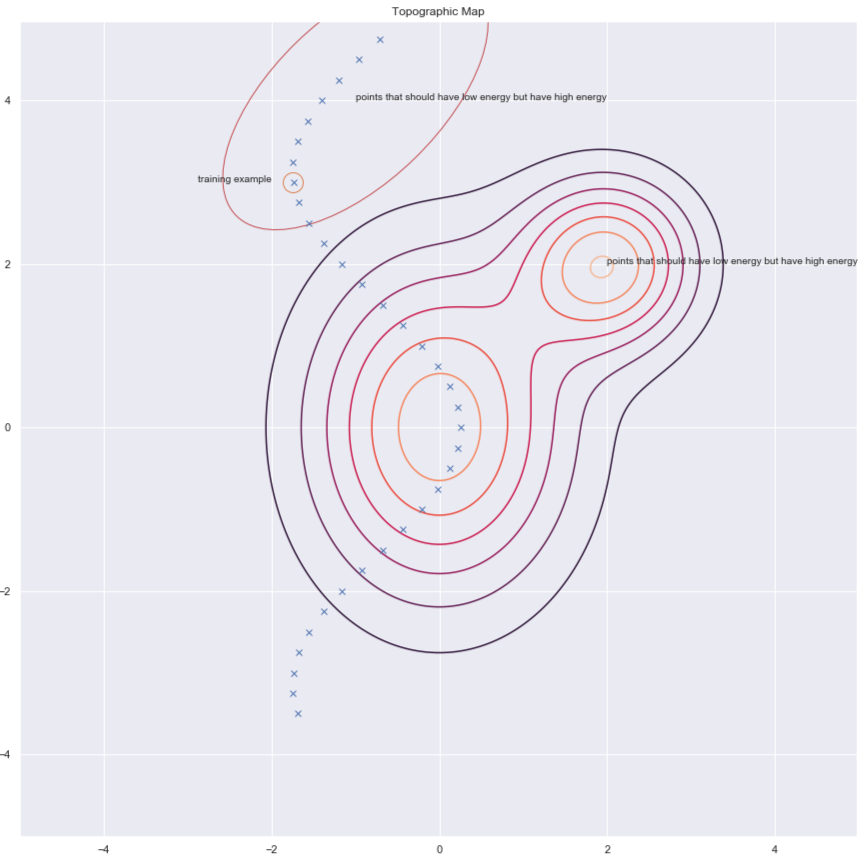
Fig. 6: metodi contrastivi

Ci sono svariati modi di identificare le candidate $y$ alle quali andremo ad aumentare l’energia. Alcuni esempi sono:

1. denoising autoencoder (autoencoder per la riduzione del rumore)
2. divergenza contrastiva
3. metodo Monte Carlo
4. catene di Markov Monte Carlo
5. Monte Carlo ibrido

Qui tratteremo brevemente gli autoencoder per la riduzione del rumore e la divergenza contrastiva.

Autoencoder per la riduzione del rumore (denoising autoencoder, DAE)

Un modo per rintracciare le $y$ alle quali aumentare l’energia è tramite la perturbazione casuale dell’esempio di addestramento, come esemplificato dalle frecce verdi nel grafico qui sotto:

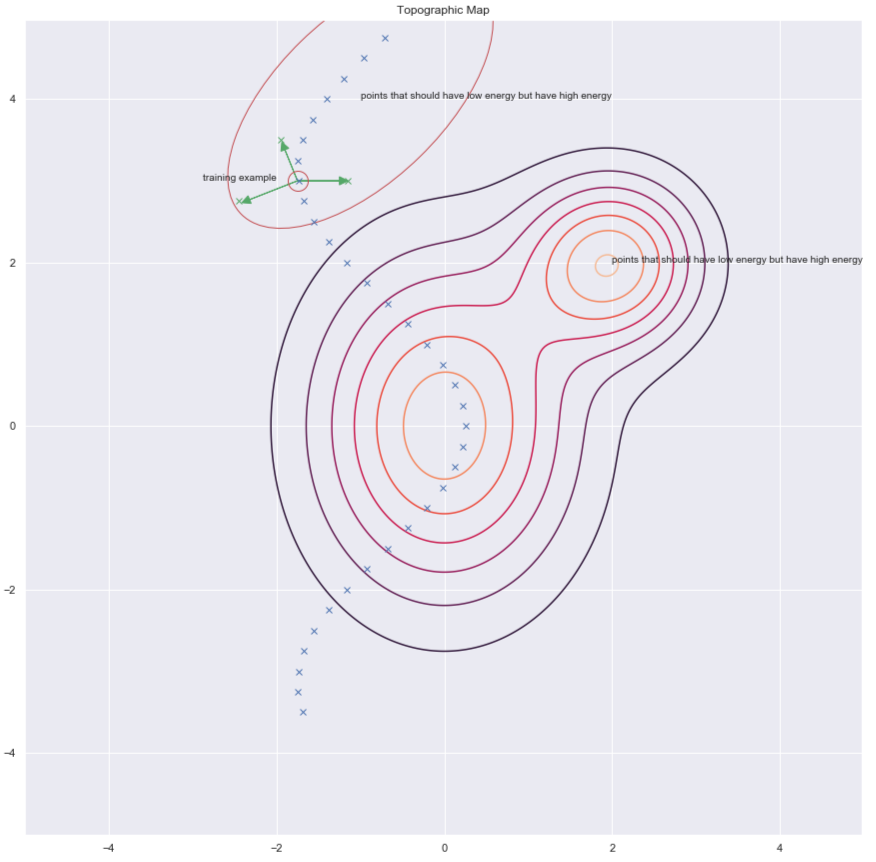
Fig. 7: mappa topografica

Una volta perturbato il dato, possiamo incrementarne l’energia in questo punto. Se ripetiamo ciò per un numero sufficiente di volte per tutti i dati, i campioni dell’energia si raggomitoleranno attorno agli esempi di addestramento. Il seguente grafico illustra come viene operato l’addestramento:

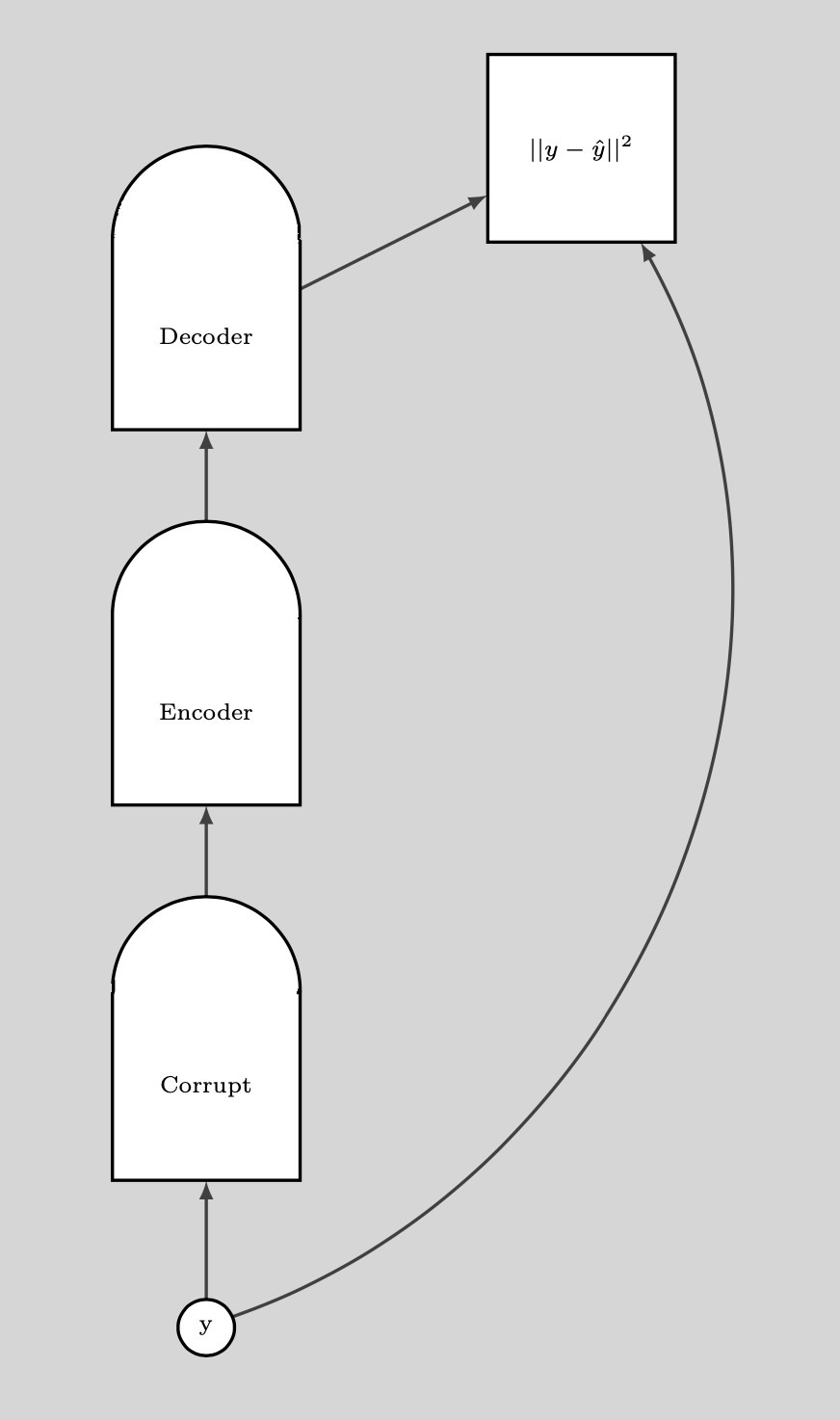
Fig. 8: l'addestramento

Procedura per l’addestramento:

1. Considerare un punto $y$ e perturbarlo
2. Addestrare un encoder e un decoder per ricostruire il dato originale a partire dal punto perturbato

Se il DAE è addestrato correttamente, l’energia crescerà in maniera quadratica come ci spostiamo dalla varietà dei dati.

Il grafico seguente illustra come si utilizzano i DAE.

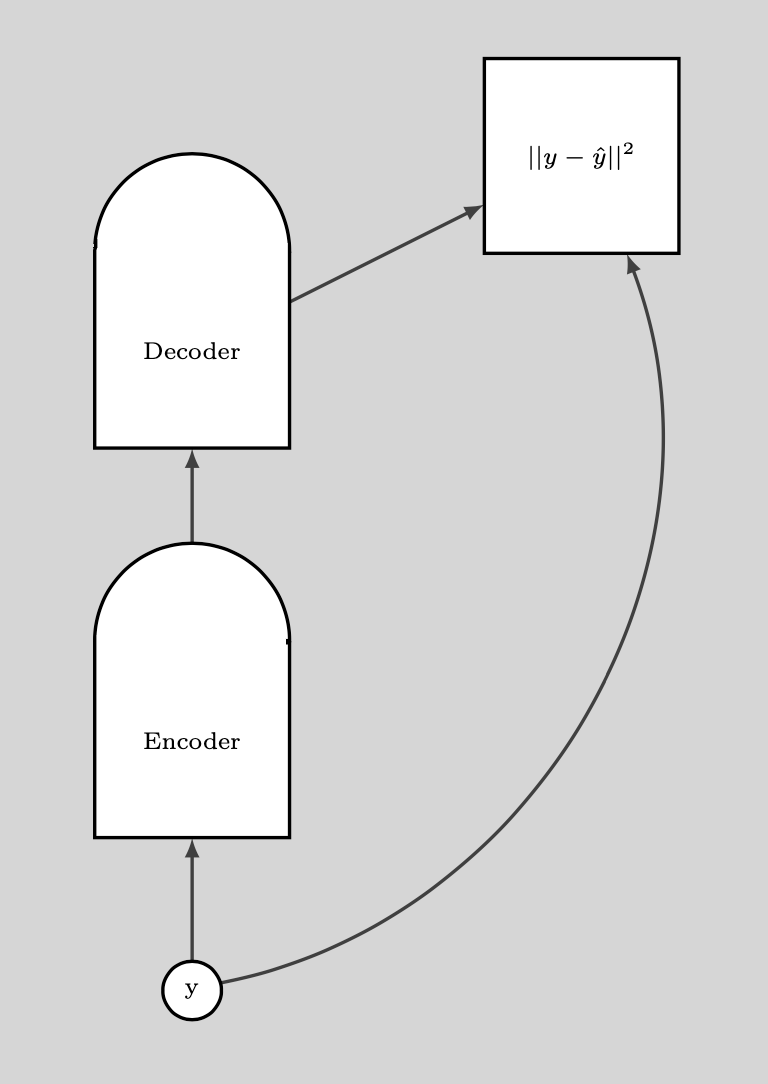
Fig. 9: utilizzo di un DAE

BERT

BERT è addestrato in maniera analoga, con la differenza che lo spazio è discreto in quanto stiamo lavorando sul linguaggio. La tecnica di perturbazione consiste nel mascherare alcune delle parole e la fase di ricostruzione consiste prevedere le parole mancanti, ragione per cui questo metodo è chiamato autoencoder mascherato (masked autoencoder).

Divergenza contrastiva

La divergenza contrastiva ci propone un metodo più intelligente per trovare i punti $y$ per i quali vogliamo aumentare l’energia. Possiamo dare una perturbazione casuale a uno dei nostri punti di addestramento e quindi muoverci giù lungo il paesaggio della funzione di energia usando la discesa del gradiente. Alla fine della traiettoria, aumentiamo l’energia per il punto su cui terminiamo. Ciò è illustrato dalla linea verde nel grafico qui sotto.

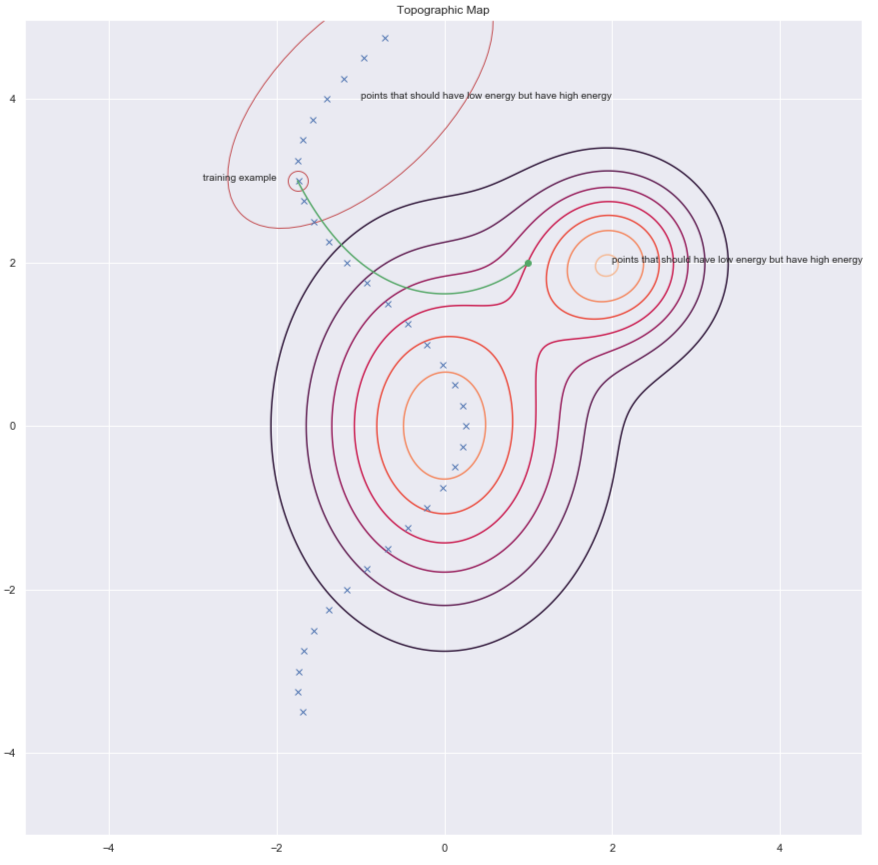
Fig. 10: divergenza contrastiva