Modelli ad Energia (EBM, Energy-Based Models)

Panoramica

Introduciamo un nuovo quadro per la definizione di modelli, che fornisce un sistema unificato per la creazione di modelli supervisionati, non-supervisionati e auto-supervisionati. I modelli ad energia (EBM, Energy-Based Models) osservano un insieme di variabili di ingresso $x$ e un insieme di variabili di uscita $y$. Per spiegarne l’utilità, pensiamo a due casi problematici principali in cui la formulazione classica di classificatori neurali feed-forward non risulta adeguata:

1. il caso in cui la procedura necessaria per l’inferenza richiede un calcolo più complesso di quello realizzabile attraverso una serie finita di somme ponderate.
2. il caso in cui il problema ammette più di un output per un singolo input. Per esempio, si consideri il problema di predirre fotogrammi successivi in un video. Generalmente, una rete neurale per la classificazione viene allenata in modo tale che emetta un punteggio per ogni classe presente nel problema. Tuttavia, ciò non è possibile in un campo continuo ad alta dimensionalità come quello delle immagini: non possiamo calcolare una funzione softmax che indichi l’immagine corretta tra tutte quelle possibili, come invece facciamo con le classi in un problema di classificazione ordinario. Anche se l’output fosse discreto, potrebbe comunque avere una cardinalità molto elevata. Per esempio, il testo, come formato, ha proprietà compositive, il che porta ad avere un enorme numero di possibili combinazioni valide da considerare. Gli EMB forniscono un struttura migliore per trattare questi tipi di dati.

L’Approccio EMB

Invece di provare a categorizzare le $x$ secondo i valori di $y$, ciò che vogliamo fare è calcolare se una coppia ($x$, $y$) sia opportuna oppure no, data la distribuzione dei dati. In altre parole, vorremmo trovare una $y$ che sia compatibile con l’input $x$. Il problema può anche essere posto come la ricerca di una $y$ per cui il valore di una funzione $F(x,y)$ sia basso. Come esempi pratici:

• $y$ è una fedele versione ad alta risoluzione di $x$?
• Il testo A è una corretta traduzione del testo B?

Definizione

Definiamo una funzione scalare di energia $F: \mathcal{X} \times \mathcal{Y} \rightarrow \mathcal{R}$ dove $F(x,y)$ descrive il livello di affinità per la coppia $(x,y)$. Valori elevati di $F$ indicano abbinamenti incompatibili, mentre valori bassi indicano una buona compatibilità tra $x$ e $y$. (N.B.: quest’energia è minimizzata durante l’inferenza, non durante l’apprendimento.) L’inferenza è eseguita secondo l’equazione seguente:

Soluzione: inferenza basata sul gradiente

Richiediamo che la funzione di energia sia liscia e differenziabile, in modo tale da permettere l’inferenza attraverso metodi incentrati sull’uso del gradiente. Per effettuare l’inferenza, minimizziamo questa funzione usando la discesa del gradiente per trovare $y$ compatibili. Esistono anche molti metodi alternativi all’uso del gradiente per ottenere il minimo di una funzione.

Parentesi: I modelli grafici sono un caso speciale dei modelli ad energia. La loro funzione di energia è scomponibile in una somma di termini energetici. Ogni addendo prende in considerazione un sottoinsieme delle variabili del sistema. Se organizzati in configurazioni apposite, esistono algoritmi di inferenza efficienti per calcolare il minimo di una somma di termini rispetto alla variabile che siamo interessati ad inferire.

EBM a Variabili Latenti

In questi tipi di problema, la variabile di uscita $y$ dipende sia da $x$ sia da un’altra variabile $z$ (la variabile latente), di cui non conosciamo il valore in quanto non viene osservata. Queste variabili latenti possono fornire informazioni ausiliarie utili alla risoluzione del problema.

Un esempio di variabile latente può essere la posizione degli estremi di ogni parola in un blocco di testo in un contesto in cui, per esempio, si cerca di interpretare una frase scritta senza spazi, o una frase pronunciata, qualora la separazione tra parole fosse difficile da individuare. Per esempio, lingue come il francese hanno confini spesso quasi impercettibili tra le parole. Per cui, avere a disposizione questa variabile latente (la separazione tra la parole, in questo esempio) nel modello risulterebbe molto efficace per l’interpretazione dei dati in entrata. In quanto latenti, il valore di queste variabili non è però conosciuto, e bisogna ricorrere ad altri metodi per gestirle.

Inferenza

Per eseguire l’inferenza con EBM a variabili latenti, si deve minimizzare la funzione di energia rispetto a $y$ e $z$ in maniera simultanea.

Ciò è equivalente a una ridefinizione della funzione di energia a favore della forma:

\(F_\infty(x,y) = \text{argmin}_{z}E(x,y,z)\), con \(F_\beta(x,y) = -\frac{1}{\beta}\log\int_z \exp(-\beta E(x,y,z)).\)

Quando $\beta \rightarrow \infty$, allora $\check{y} = \text{argmin}_{y}F(x,y)$.

Un altro vantaggio nell’includere variabili latenti è la possibilità, facendo variare le variabili latenti all’interno di un certo intervallo, di far a sua volta variare la previsione in uscita $y$ nella varietà di possibili previsioni (il nastro è mostrato nella figura sotto).

Questo permette alla macchina di produrre molteplici output, invece di uno solo.

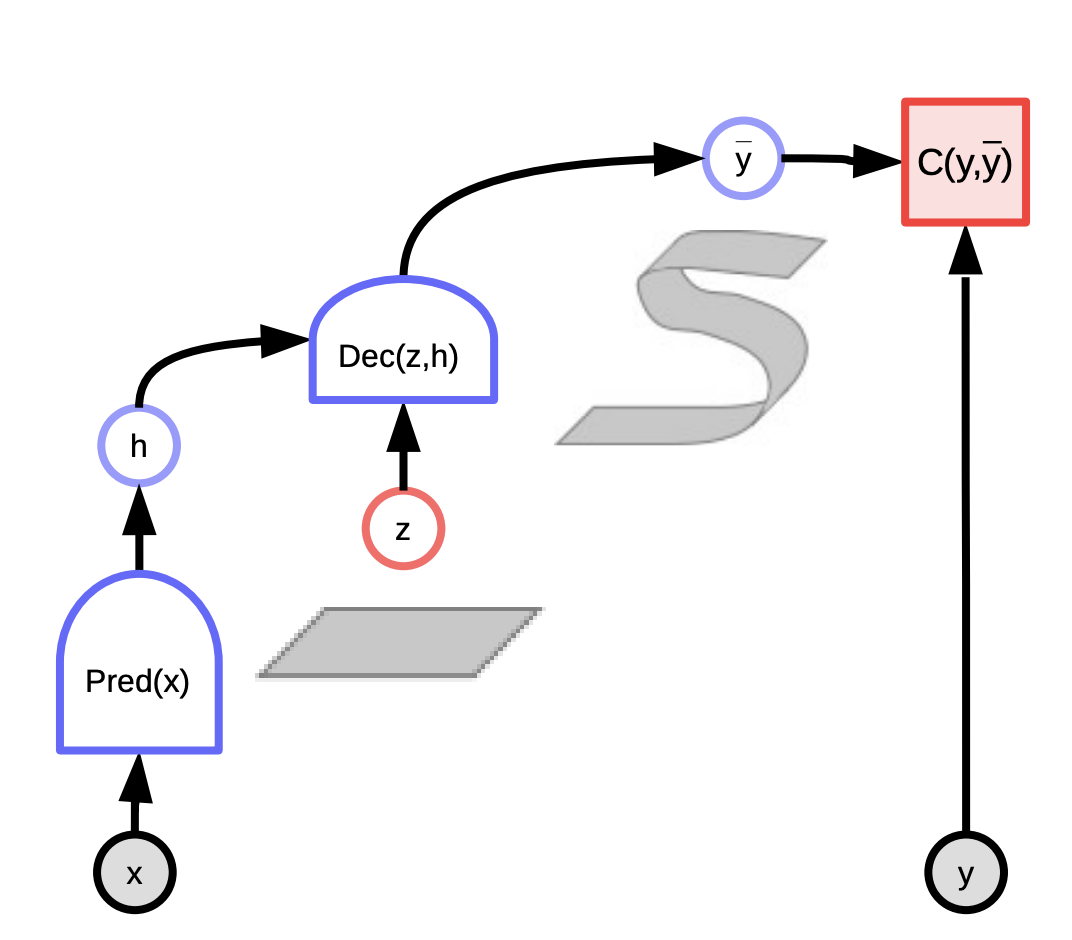
Fig. 1: Grafo computazionale di un modello ad energia.

Esempi

Un esempio pertinente è la previsione di fotogrammi in un filmato. Esistono svariate applicazioni di questa tecnologia, tra cui la compressione di video, o l’uso di filmati raccolti da auto a guida autonoma per dedurre il comportamento di altre vetture. Invece di produrre una singola previsione, spesso uguale alla media di tutti i fotogrammi plausibili, l’EBM è in grado di produrre varie immagini individualmente realistiche condizionate dalle variabili $z$. Variando $z$ si può attraversare ed esplorare lo spazio delle immagini prodotte dal modello.

Un altro esempio è la traduzione di testo. La traduzione è da sempre un problema difficile per via dell’inesistenza di una singola traduzione corretta di un testo da una lingua a un’altra. Solitamente, esistono diversi modi di esprimere un concetto, ed è difficile trovare ragioni per preferirne uno a un altro. Sarebbe, dunque, vantaggioso poter parametrizzare tutte le possibili traduzioni che un sistema è in grado di produrre a partire da un testo dato in termini di variabili latenti $z$. Per esempio, ipotizziamo di voler tradurre un testo dal tedesco all’inglese: esiste più di una traduzioone corretta, e modificando delle variabili latenti saremmo in grado di modificare la traduzione prodotta dal modello esplorandone lo spazio.

Modelli ad Energia vs. Modelli Probabilistici

Le energie possono essere considerate come probabilità logaritmiche non normalizzate; si può quindi usare la distribuzione di Boltzmann per convertire l’energia in probabilità con l’apposita normalizzazione:

dove $\beta$ è una costante positiva che può essere calibrata a seconda del modello. Valori elevati di $\beta$ tendono a creare un modello che produce una funzione a frequenze più alte dove la probabilità è fortemente concentrata in alcuni punti e vicina a zero altrove, mentre valori bassi di $\beta$ rendono la funzione più regolare. (In fisica, $\beta$ è il reciproco della temperatura: $\beta \rightarrow \infty$ significa che la temperatura tende a zero).

Se marginalizziamo $z$: $P(y \mid x) = \int_z P(y,z \mid x)$, otteniamo:

Perciò, in presenza di una variabile latente $z$, per eliminarla in maniera corretta a livello probabilistico, si può ridefinire la funzione energetica $E$ a favore di $F_\beta$ (Energia Libera).

Energia Libera

Calcolare questa quantità non è sempre semplice… Infatti, nella maggior parte dei casi, il problema diventa intrattabile. In presenza di una variabile latente rispetto a cui minimizzare il modello o marginalizzare (che è ciò che succede quando definiamo questa funzione di energia $F$), nel qual caso il problema di minimizzazione corrispone al limite per $\beta$ che va a infinito, allora il problema diventa risolvibile.

Nella definizioone di $F_\beta(x, y)$ qui sopra, $P(y \mid x)$ è semplicemente il risultato dell’applicazione della formula di Boltzmann e $z$ è stata marginalizzata in maniera implicita al suo interno. I fisici chiamano questa quantità l’“energia libera” (free energy, in inglese), ed è per questo che la identifichiamo con la lettera $F$. $E$ è l’energia, $F$ è l’energia libera.

Domanda: quali sono i vantaggi dei modelli ad energia? Nei modelli probabilistici, è comunque possibile avere variabili latenti e marginalizzarle.

La differenza è che nei modelli probabilistici non abbiamo modo di scegliere la funzione obiettivo da minimizzare e, per aderire al framework probabilistico, ogni oggetto che manipoliamo deve essere una distribuzione normalizzata (che può essere approssimata tramite metodi variazionali, ecc.). Qui, invece, in concreto, l’obiettivo è prendere decisioni. In un sistema di guida autonoma, per esempio, data una probabilità di 0.8 di girare a sinistra e una probabilità di 0.2 di girare a destra, le decisione sarà di girare a sinistra. Il valore esatto delle probabilità non ha importanza; ciò che importa è la scelta binaria, perchè costretti a prendere una decisione concreta. Le probabilità sono dunque irrilevanti in confronto all’attuazione della decisione. Se invece si vuole combinare l’output di due sistemi separati (per esempio, uno umano e uno artificiale) e questi sistemi non sono stati creati ed allenati assieme, si dovranno calibrare i loro risultati in modo da combinarli prima di prendere una decisione. Per calibrare i risultati, bisogna trasformarli in probabilità. Se invece si crea un sistema decisionale end-to-end, dove tutte le parti sono al corrente della presenza delle altre parti e sono ottimizzate in unisono, allora qualsiasi funzione di punteggio è consentita, purchè assegni il punteggio più alto alla miglior decisione. I modelli ad energia lasciano, quindi, più scelta nella costruzione, nell’apprendimento, e nell’obiettivo del modello. Se invece insistiamo nella scelta di un modello probabilistico, allora bisogna utilizzare il metodo della massima verosimiglianza; in pratica, il modello deve essere allenato in modo tale che la probabilità dei dati osservati sia massima. Il problema è che è provato che funzioni solo quando il modello è “corretto”, e un modello non è mai corretto. Per citare un grande statistico George Box, “Tutti i modelli sono sbagliati, ma alcuni sono utili”. I modelli probabilistici, quindi, specialmente quelli in spazi ad alta dimensionalità o in spazi combinatori come il linguaggio di testo, sono tutti modelli approssimativi. A loro modo, sono tutti sbagliati, e se proviamo a normalizzarli, li rendiamo ancora più sbagliati. Quindi è meglio non normalizzarli ed utilizzare le energie.

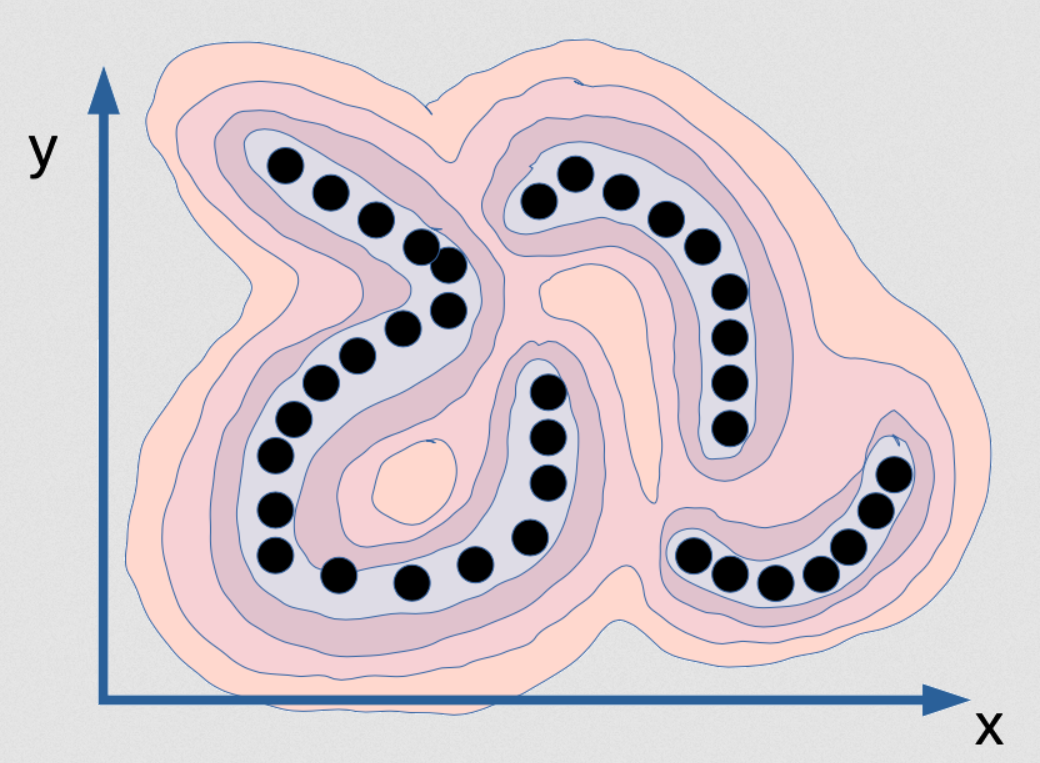
Fig. 2: Visualizzazione della funzione di energia che mostra la dipendenza tra $x$ e $y$ come funzione implicita

Questa funzione di energia mostra la relazione tra $x$ e $y$. È simile ad un territorio montuoso, se vogliamo trovare un’analogia. La vallate corrispondono alla presenza dei dati, mentre le montagne si elevano tutto intorno. Per allenare un modello probabilistico, immaginiamo che i punti esistano su una varietà topologica sottile e infinita. La distribuzione di dati per i dati rappresentati dai pallini neri è dunque una semplice linea, senza spessore, nello specifico tre segmenti, in questo esempio. Allenando un modello probabilistico su questi dati, il modello di densità ideale dovrebbe essenzialmente corrispondere a questa varietà. Su questa varietà, la densità dovrebbe essere infinita, mentre anche solo a un’$\epsilon$ di distanza, la densità dovrebbe tendere a zero. Non solo la densità dovrebbe essere infinita in questo spazio, ma l’integrale nelle variabili di integrazione $x$ e $y$ dovrebbe essere uguale a 1. Questo, però, è difficile da ottenere, a livello di implementazione su un computer, ed è praticamente impossibile in generale. Per calcolare questa funzione con una rete neurale, per esempio, questa dovrebbe avere un numero infinito di parametri, calibrati in maniera tale che l’integrale del risultato fornito dal sistema sull’intero dominio sia 1; il che è impossibile, in pratica. Questa è la soluzione richiesta dal metodo della massima verosimiglianza, e nessun computer è in grado di modellarla. Tra l’altro, tale modello non sarebbe nemmeno tanto utile. Se anche avessimo il modello di densità perfetto per questo esempio partico, non potremmo comunque svolgere l’inferenza. Dato un valore di $x$, il valore corretto di $y$ sarebbe comunque impossibile da trovare attraverso un algoritmo, perchè tutti i valori di $y$, al di là di quelli in un insieme di misura nulla, hanno probabilità uguale a zero, e solo un numero discreto di valori è fattibile come soluzione. La funzione, in questo caso, corrisponderebbe a una somma di funzioni delta di Dirac. In questo esempio:

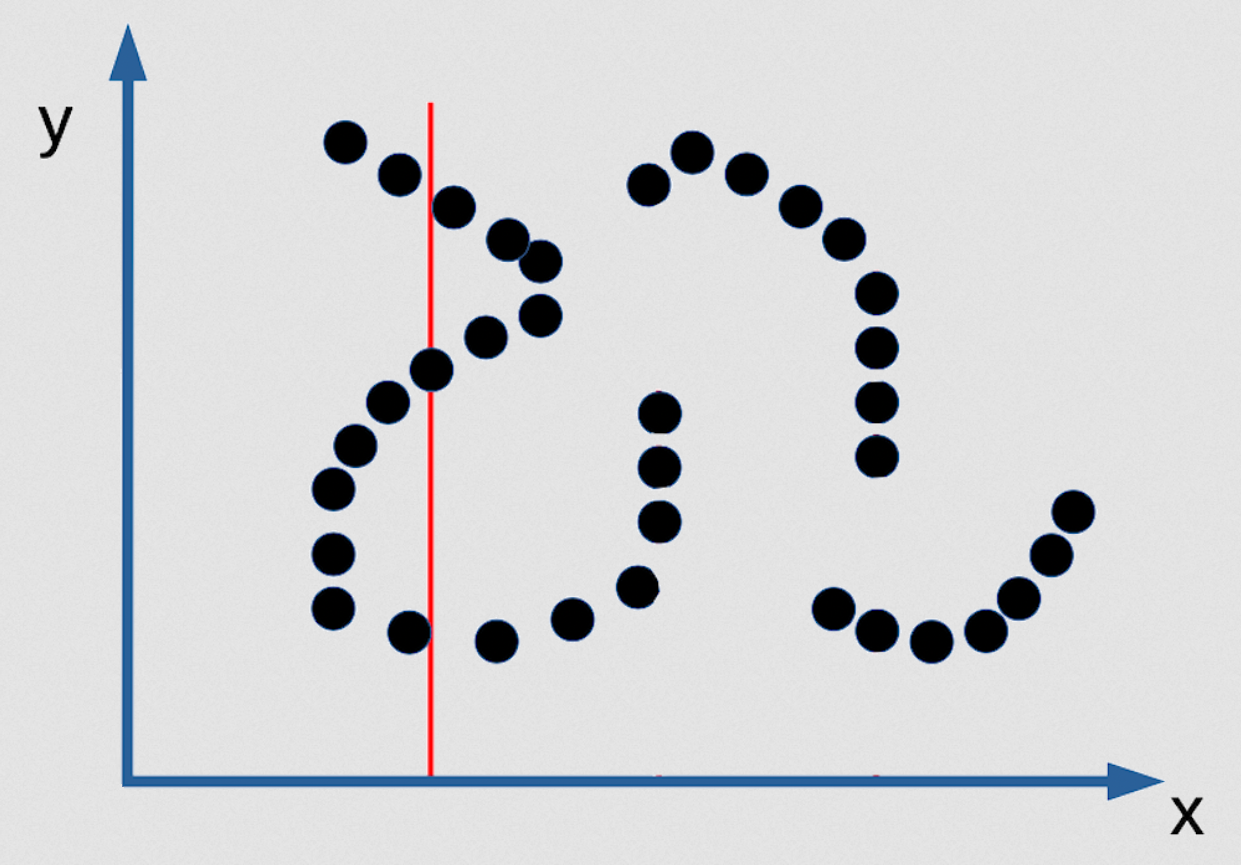
Fig. 3: Esempio di molteplici previsioni valide in un EBM

Ci sono 3 valori di $y$ possibili in questo caso, ma questi sono punti di larghezza finita, quindi impossibili da trovare. Nessun algoritmo di inferenza sarebbe in grado di trovarli. L’unico modo per arrivare a una soluzione è utilizzare una funzione di confronto liscia e differenziabile, per poi procedere con la discesa del gradiente fino a trovare un valore accettabile di $y$ per ogni valore di $x$. Ma, in questo caso, il modello probabilistico non sarebbe un modello corretto per il tipo di distribuzione in questo esempio. Questo esempio dimostra, dunque, come l’insistenza su un modello probabilistico non sia una buona idea in queste circostanze.

I bayesiani potrebbero controbattere che il modo di sopperire a questo problema sia di imporre una distribuzione di probabilità a priori che preferisca una funzione di densità liscia. Ma qualsiasi formulazione in termini bayesiani, tralasciando la normalizzazione, è equivalente ad un EBM. Modelli ad energia con regolarizzazione, che si manifesta come un ulteriore addendo nella funzione di energia, sono equivalenti ai modelli bayesiani in cui la verosimiglianza è una funzione esponenziale dell’energia: $\exp(\text{energia}) \times \exp(\text{regolarizzazione}) = \exp(\text{energia} + \text{regolarizzazione})$. Il logaritmo della parte destra corrisponde a un modello ad energia con l’aggiunta della regolarizzazione.

C’è quindi una corrispondenza tra modelli probabilistici e metodi bayesiani, ma insistere nell’utilizzo del metodo della massima verosimiglianza può talvolta essere controproducente, specialmente in spazi ad alta dimensionalità o spazi combinatori dove il modello probabilistico è molto impreciso. Nel caso di ditribuzioni discrete, l’errore può essere accettabile, ma nel caso di distribuzioni continue, il modello potrebbe risultare del tutto incorretto.