RNNs, GRUs, LSTMs, Attenzione, Seq2Seq, e Reti di Memoria

Architetture di apprendimento profondo

Nell’apprendimento profondo, ci sono diversi moduli per realizzare funzioni diverse. La competenza nell’ambito dell’apprendimento profondo implica la progettazione di architetture per risolvere compiti particolari. Simile alla scrittura di programmi con algoritmi per fornire istruzioni a un computer nel passato, l’apprendimento profondo riduce una funzione complessa ad un grafo di moduli funzionali (possibilmente dinamici), le cui funzioni sono finalizzate dall’apprendimento.

Come per quello che abbiamo visto con le reti convoluzionali, l’architettura delle reti è importante.

Reti ricorrenti

In una rete neurale convoluzionale, il grafico o le interconnessioni tra i moduli non possono avere dei loop. Esiste almeno un ordine parziale tra i moduli in modo tale che gli input alla rete siano disponibili quando calcoliamo le uscite.

Come mostrato in Figura 1, ci sono dei cicli nelle reti neurali ricorrenti.

Figura 1. Reti ricorrenti con loop

• $x(t)$ : input che cambia nel tempo
• $\text{Enc}(x(t))$: codificatore che genera una rappresentazione dell’input
• $h(t)$: rappresentazione dell’input
• $w$: parametri addestrabili
• $z(t-1)$: precedente stato nascosto, il quale è l’output del precedente passo temporale
• $z(t)$: stato nascosto corrente
• $g$: funzione che può essere una rete neurale complessa; uno degli input è $z(t-1)$ che è l’output del passo temporale precedente
• $\text{Dec}(z(t))$: decodificatore che genera l’output

Reti ricorrenti: srotolare il ciclo

Srotolare il ciclo lungo la dimensione temporale. L’input è una sequenza $x_1, x_2, \cdots, x_T$.

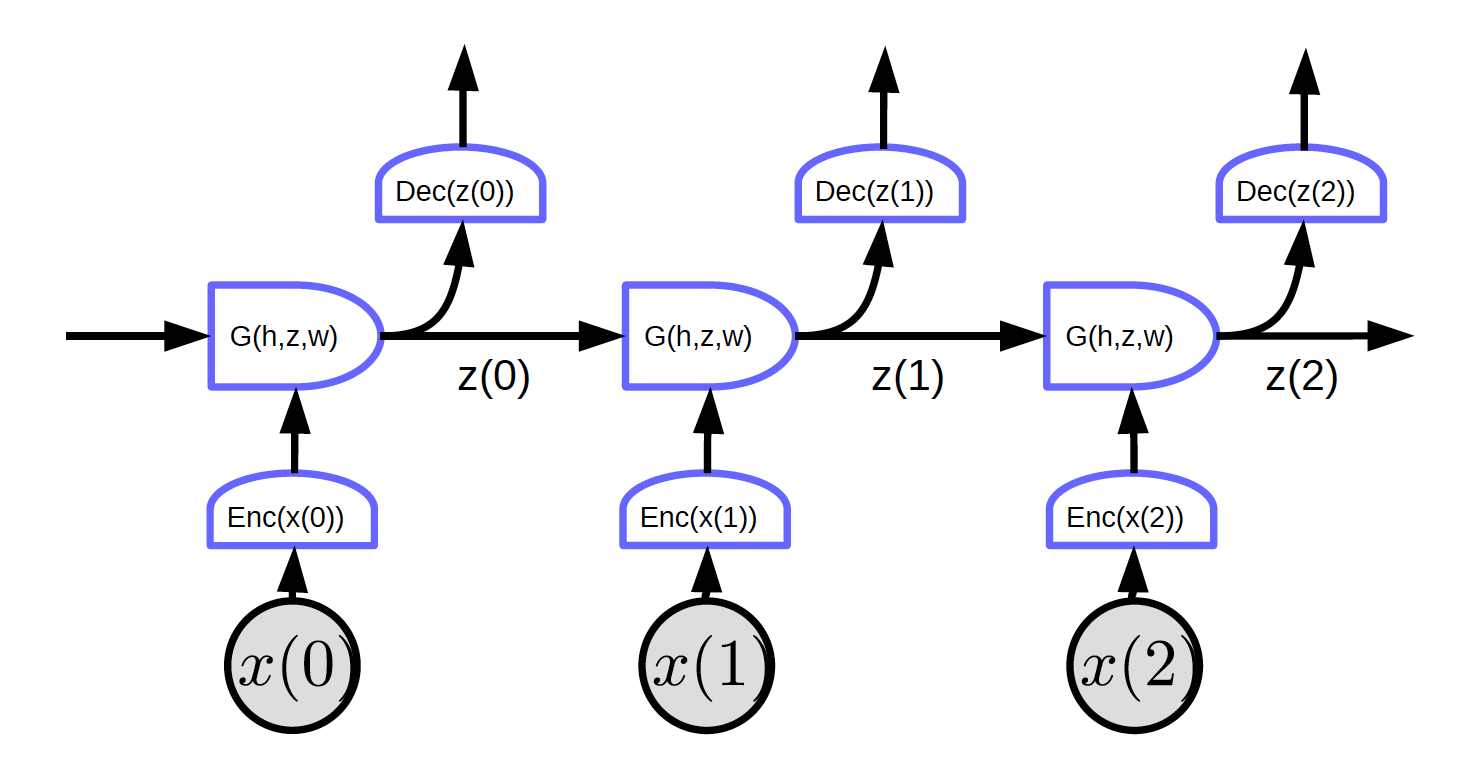
Figura 2. Reti ricorrenti con un ciclo srotolato

In Figura 2, l’input è $x_1, x_2, x_3$

Al tempo t = 0, l’ingresso $x (0)$ viene passato all’encoder che genera la rappresentazione $h(x(0)) = \text{Enc}(x(0))$ e poi lo passa a G per generare lo stato nascosto $z(0) = G(h_0, z’, w)$. Per $t = 0$, $z’$ in $G$ può essere inizializzato a $0$ o inizializzato casualmente. $z(0)$ viene passato sia al decodificatore per generare un output sia al passo temporale successivo.

Poiché non ci sono loop in questa rete e possiamo implementare la backpropagation.

La Figura 2 mostra una rete regolare con una caratteristica particolare: ogni blocco condivide gli stessi pesi. Tre codificatori, decodificatori e funzioni G hanno gli stessi pesi rispettivamente attraverso diversi passi temporali.

BPTT: retropropagazione nel tempo (BPTT, Backprop through time). Sfortunatamente, BPTT non funziona così bene nella forma naive delle RNN.

Problemi con RNN:

1. Scomparsa del gradiente
   • In una lunga sequenza, i gradienti vengono moltiplicati per la matrice del peso (trasposizione) ad ogni passo temporale. Se ci sono piccoli valori nella matrice del peso, la norma dei gradienti diventa esponenzialmente sempre più piccola.
2. Esplosione del gradiente
   • Se abbiamo una matrice di peso con valori elevati e la non linearità nello strato ricorrente non satura, i gradienti esploderanno. I pesi divergeranno nella fase di aggiornamento. Potrebbe essere necessario utilizzare un learning rate molto piccolo per riuscire a far funzionare la discesa del gradiente.

Uno dei motivi per utilizzare gli RNN è il vantaggio di ricordare le informazioni in passato. Tuttavia, potrebbe non riuscire a memorizzare le informazioni molto tempo fa in un semplice RNN senza trucchi.

Un esempio che presenta un problema di scomparsa del gradiente:

L’input sono i caratteri di un programma C. Il sistema dirà se si tratta di un programma sintatticamente corretto. Un programma sintatticamente corretto dovrebbe avere un numero valido di parentesi graffe, quadre e tonde. Pertanto, la rete dovrebbe ricordare quante parentesi aperte ci sono da verificare e se le abbiamo chiuse tutte. La rete deve archiviare tali informazioni in stati nascosti come un contatore. Tuttavia, a causa della scomparsa del gradiente, la rete non riuscirà a conservare tali informazioni se il programma è sufficientemente lungo.

Stratagemmi per RNN

• taglio dei gradienti: (evita l’esplosione dei gradienti) Schiaccia i gradienti quando diventano troppo grandi.
• Inizializzazione (iniziare nel campo di gioco giusto evita l’esplosione/scomparsa dei gradienti) Inizializza le matrici dei pesi per preservare la norma ad una certa misura. Ad esempio, l’inizializzazione ortogonale inizializza la matrice del peso come matrice ortogonale casuale.

Moduli moltiplicativi

Nei moduli moltiplicativi piuttosto che calcolare solo una somma ponderata di input, calcoliamo i prodotti degli input e quindi calcoliamo la somma ponderata di quest’ultimi.

Supponiamo che $x \in {R}^{n\times1}$, $W \in {R}^{m \times n}$, $U \in {R}^{m \times n \times d}$ and $z \in {R}^{d\times1}$. Qui U è un tensore.

\(w_{ij} = u_{ij}^\top z = \begin{pmatrix} u_{ij1} & u_{ij2} & \cdots &u_{ijd}\\ \end{pmatrix} \begin{pmatrix} z_1\\ z_2\\ \vdots\\ z_d\\ \end{pmatrix} = \sum_ku_{ijk}z_k\)

\(s = \begin{pmatrix} s_1\\ s_2\\ \vdots\\ s_m\\ \end{pmatrix} = Wx = \begin{pmatrix} w_{11} & w_{12} & \cdots &w_{1n}\\ w_{21} & w_{22} & \cdots &w_{2n}\\ \vdots\\ w_{m1} & w_{m2} & \cdots &w_{mn} \end{pmatrix} \begin{pmatrix} x_1\\ x_2\\ \vdots\\ x_n\\ \end{pmatrix}\)

ove, $s_i = w_{i}^\top x = \sum_j w_{ij}x_j$.

L’output del sistema è una classica somma ponderata di input e pesi. Questi pesi sono a loro volta una somma ponderate di pesi e input.

Architettura di una Hypernetwork: i pesi sono calcolati da un’altra rete.

Meccanismo di attenzione

$x_1$ e $x_2$ sono vettori, $w_1$ e $w_2$ sono scalari dopo softmax dove $w_1 + w_2 = 1$ e $w_1$ e $w_2$ sono compresi tra 0 e 1.

$w_1x_1 + w_2x_2$ è una somma ponderata di $x_1$ e $x_2$ ponderata per coefficienti $w_1$ e $w_2$.

Modificando la dimensione relativa di $w_1$ e $w_2$, possiamo cambiare l’output di $w_1x_1 + w_2x_2$ in $x_1$ o $x_2$ o alcune combinazioni lineari di $x_1$ e $x_2$.

Gli input possono avere più vettori $x$ (più di $x_1$ e $x_2$). Il sistema sceglierà una combinazione appropriata, la cui scelta è determinata da un’ulteriore variabile z. Un meccanismo di attenzione consente alla rete neurale di focalizzare la sua attenzione su particolari input ed ignorarne altri.

L’attenzione è sempre più importante nei sistemi elaborazione del linguaggio naturale (NLP, Natural Language Processing) che utilizzano architetture di trasformatori o altri tipi di meccanismi di attenzione.

I pesi sono indipendenti dai dati perché z è indipendente dai dati.

Gated Recurrent Units (GRU)

Come accennato in precedenza, le RNNs soffrono del problema della scomparsa/esplosione del gradiente e non riesce a memorizzare gli stati per un periodo temporale molto lungo. GRU, [Cho, 2014] (https://arxiv.org/abs/1406.1078), è un’applicazione di moduli moltiplicativi che tenta di risolvere questi problemi. È un esempio di rete ricorrente con memoria (un altro sono le LSTM). La struttura di un’unità GRU è mostrata di seguito:

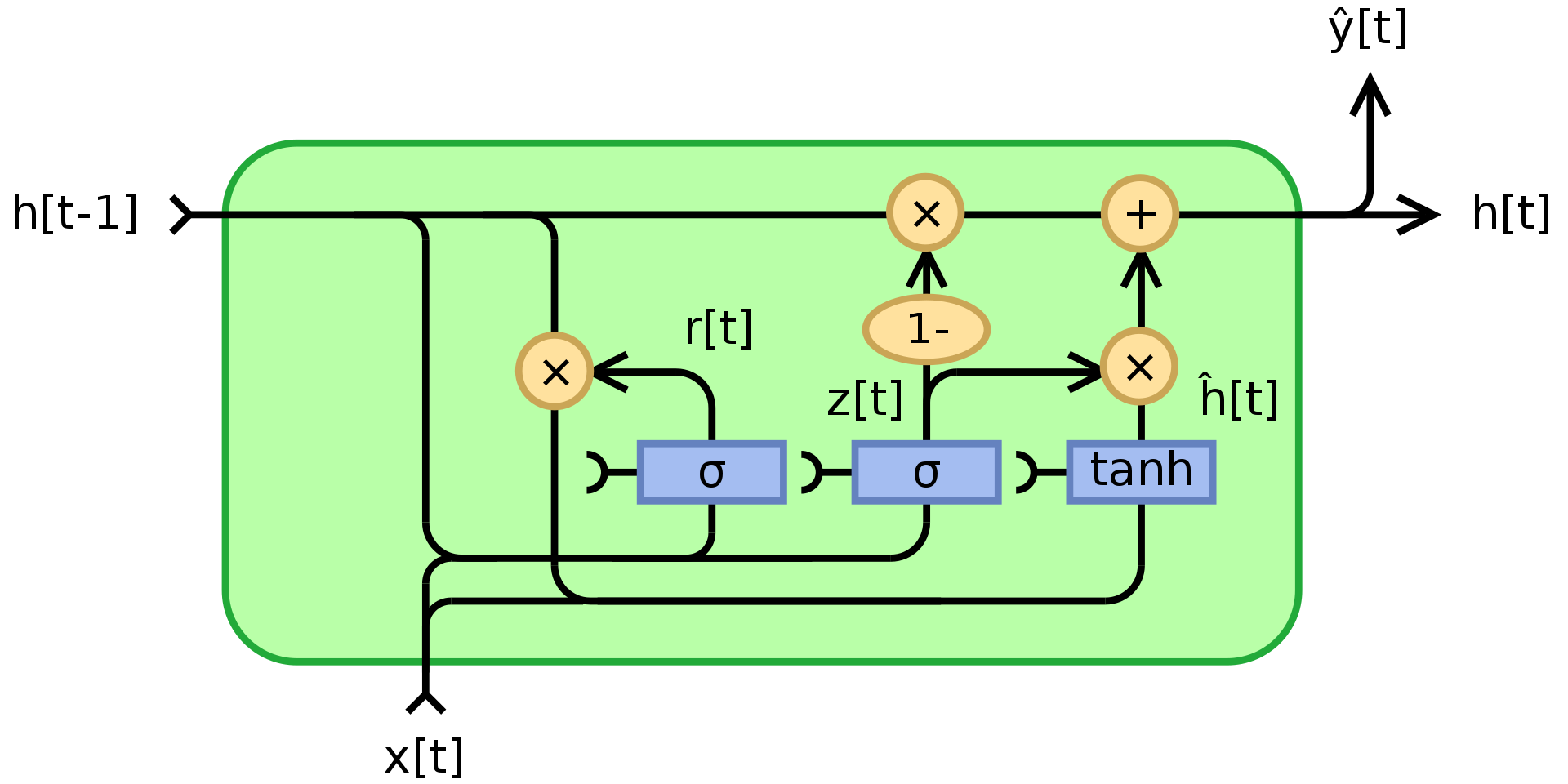
Figura 3. Gated Recurrent Unit

\(\begin{array}{l} z_t = \sigma_g(W_zx_t + U_zh_{t-1} + b_z)\\ r_t = \sigma_g(W_rx_t + U_rh_{t-1} + b_r)\\ h_t = z_t\odot h_{t-1} + (1- z_t)\odot\phi_h(W_hx_t + U_h(r_t\odot h_{t-1}) + b_h) \end{array}\)

dove $\odot$ indica la moltiplicazione degli elementi (prodotto di Hadamard), $x_t$ è il vettore di input, $h_t$ è il vettore di output, $z_t$ è il vettore del gate di aggiornamento, $r_t$ è il vettore del gate di ripristino, $\phi_h$ è una tangente iperbolica e $W$, $U$, $b$ sono parametri da apprendere.

Per essere precisi, $z_t$ è un vettore di gating che determina la quantità di informazioni passate da trasmettere nel futuro. Applica una funzione sigmoide alla somma di due strati lineari e un bias sull’input $x_t$ e lo stato precedente $h_{t-1}$. $z_t$ è un coefficiente tra 0 e 1 come risultato dell’applicazione della sigmoide. Lo stato di output finale $h_t$ è una combinazione convessa di $h_{t-1}$ and $\phi_h(W_hx_t + U_h(r_t\odot h_{t-1}) + b_h)$ via $z_t$. Se il coefficiente è 1, l’output dell’unità corrente è solo una copia dello stato precedente e ignora l’input (che è il comportamento predefinito). Se è inferiore a uno, tiene conto di alcune nuove informazioni dall’input.

Il gate di ripristino $r_t$ viene utilizzato per decidere la quantità di informazioni passate da dimenticare. Nel nuovo contenuto di memoria $\phi_h(W_hx_t + U_h(r_t\odot h_{t-1}) + b_h)$, se il coefficiente in $r_t$ è 0, non viene memorizzata nessuna delle informazioni del passato. Se allo stesso tempo $z_t$ è 0, il sistema è completamente ripristinato poiché $h_t$ guarderebbe solo l’input.

LSTM (Long Short-Term Memory)

GRU è in realtà una versione semplificata di una cella LSTM che è uscita molto prima, [Hochreiter, Schmidhuber, 1997] (https://www.bioinf.jku.at/publications/older/2604.pdf). Costruendo celle di memoria per preservare le informazioni passate, le LSTM mirano anche a risolvere i problemi di perdita di memoria a lungo termine che abbiamo visto nelle RNN. La struttura degli LSTM è mostrata di seguito:

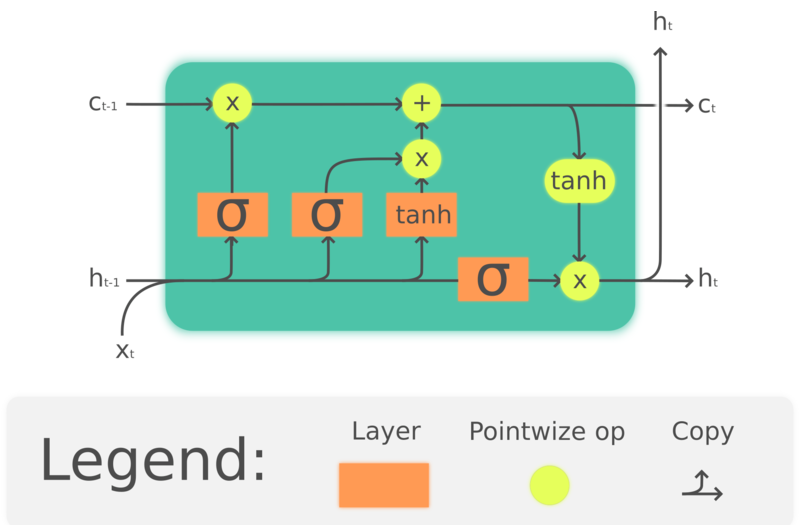
Figura 4. LSTM

\(\begin{array}{l} f_t = \sigma_g(W_fx_t + U_fh_{t-1} + b_f)\\ i_t = \sigma_g(W_ix_t + U_ih_{t-1} + b_i)\\ o_t = \sigma_o(W_ox_t + U_oh_{t-1} + b_o)\\ c_t = f_t\odot c_{t-1} + i_t\odot \tanh(W_cx_t + U_ch_{t-1} + b_c)\\ h_t = o_t \odot\tanh(c_t) \end{array}\)

dove $\odot$ indica la moltiplicazione elemento per elemento, $x_t\in\ mathbb{R}^a$ è un vettore di input per la cella LSTM, $f_t\in\mathbb{R}^h$ è il vettore di attivazione del gate per dimenticare (forget gate), $i_t\in\mathbb{R}^h$ è il vettore di attivazione del gate di input/aggiornamento, $o_t\in\mathbb{R}^h$ è il vettore di attivazione del gate di output, $h_t\in\mathbb{R}^h$ è il vettore dello stato nascosto (noto anche come output), $c_t\in\mathbb{R}^h$ è il vettore di stato della cella.

Un’unità LSTM utilizza una cella $c_t$ per trasmettere le informazioni attraverso l’unità. Essa regola come le informazioni vengono preservate o rimosse dallo stato della cella attraverso strutture chiamate gate. La porta di dimenticanza $f_t$ decide quante informazioni vogliamo conservare dallo stato della cella precedente $c_{t-1}$ osservando l’input corrente e lo stato nascosto precedente e produce un numero compreso tra 0 e 1 come coefficiente di $c_{t-1}$. $\tanh(W_cx_t + U_ch_{t-1} + b_c)$ calcola un nuovo candidato per aggiornare lo stato della cella e, come il gate di dimenticanza, il gate di input $i_t$ decide la quantità di aggiornamento da applicare. Infine, l’output $h_t$ si baserà sullo stato della cella $c_t$, ma verrà sottoposto a $\tanh$, quindi filtrato dal gate di output $o_t$.

Sebbene le LSTM siano ampiamente utilizzati nel NLP, la loro popolarità sta diminuendo. Ad esempio, il riconoscimento vocale si sta muovendo verso l’utilizzo della CNN temporale e l’NLP si sta muovendo verso l’utilizzo di trasformatori.

Modello Sequenza a Sequenza

L’approccio proposto da [Sutskever NIPS 2014] (https://papers.nips.cc/paper/5346-sequence-to-sequence-learning-with-neural-networks.pdf) è il primo sistema di traduzione automatica neurale ad avere comparabili prestazioni agli approcci classici. Utilizza un’architettura encoder-decoder in cui sia l’encoder che il decoder sono LSTM multistrato.

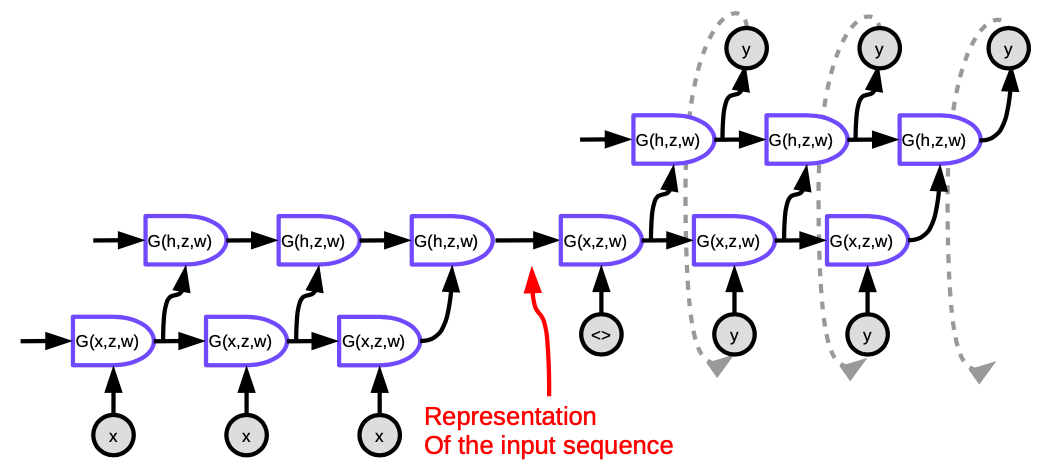
Figura 5. Seq2Seq (Sequenza a Sequenza)

Ogni cella nella figura è una LSTM. Per l’encoder (la parte a sinistra), il numero di passi temporali è uguale alla lunghezza della frase da tradurre. Ad ogni passo, c’è una pila di LSTM (quattro strati nel paper originale) in cui lo stato nascosto dell’LSTM precedente viene dato in ingresso al successivo. L’ultimo livello dell’ultima fase temporale genera un vettore che rappresenta il significato dell’intera frase, che viene quindi immesso in un’altra LSTM (il decodificatore) multistrato, che produce le parole nella lingua di destinazione. Nel decodificatore il testo viene generato in modo sequenziale; ogni passaggio produce una parola che viene inserita come input per il passaggio temporale successivo.

Due punti rendono questa architettura non soddisfacente: in primo luogo, l’intero significato della frase deve essere compresso nello stato nascosto tra l’encoder e il decoder. In secondo luogo, le LSTM in realtà non conservano le informazioni per più di circa 20 parole. La correzione di questi problemi si chiama Bi-LSTM, che esegue due LSTM in direzioni opposte. In un Bi-LSTM il significato è codificato in due vettori, uno generato eseguendo una LSTM da sinistra a destra, e un altro da destra a sinistra. Ciò consente di raddoppiare la lunghezza della frase senza perdere troppe informazioni.

Seq2seq con meccanismo di Attenzione

Il successo dell’approccio di cui sopra è stato di breve durata. Un altro articolo di Bahdanau, Cho, Bengio ha suggerito che invece di avere una rete gigantesca che comprime il significato dell’intera frase in un singolo vettore, avrebbe più senso se ad ogni passo temporale focalizzassimo l’attenzione solo sugli elementi rilevanti della frase in lingua originale con significato equivalente, cioè il meccanismo di attenzione.

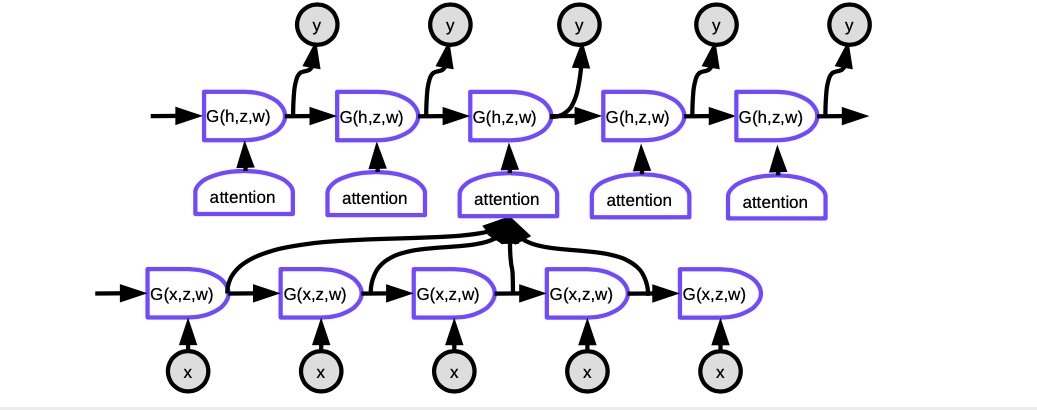
Figura 6. Seq2Seq con Attenzione

Nei modelli con attenzione, per produrre la parola corrente ad ogni passo temporale, dobbiamo prima decidere su quali rappresentazioni nascoste delle parole nella frase di input concentrarci. In sostanza, una rete imparerà a valutare in che misura ciascun ingresso codificato corrisponde all’uscita corrente del decodificatore. Questi punteggi sono normalizzati da un softmax, quindi i coefficienti vengono utilizzati per calcolare una somma ponderata degli stati nascosti nell’encoder in diverse fasi temporali. Regolando i pesi, il sistema può regolare l’area dell’input su cui concentrarsi. La magia di questo meccanismo è che la rete utilizzata per calcolare i coefficienti può essere addestrata attraverso la backpropagation. Non è necessario costruirseli a mano!

I meccanismi di attenzione hanno trasformato completamente la traduzione automatica neurale. Successivamente, Google ha pubblicato un documento Attention Is All You Need e ha presentato il trasformatore, dove ogni strato e gruppo di neuroni utilizza il meccanisdmo di attenzione.

Reti di Memoria

Le reti di memoria derivano dal lavoro a Facebook avviato da Antoine Bordes nel 2014 e Sainbayar Sukhbaatar nel 2015 .

L’idea di una rete di memoria è che ci sono due parti importanti nel tuo cervello: una è la corteccia, dove si trova la memoria a lungo termine. C’è un gruppo separato di neuroni chiamato ippocampo che invia dei fili quasi ovunque nella corteccia. Si pensa che l’ippocampo sia usato per la memoria a breve termine, ricordando le cose per un periodo di tempo relativamente breve. La teoria prevalente è che quando uno dorme, ci siano molte informazioni trasferite dall’ippocampo alla corteccia per essere solidificate nella memoria a lungo termine poiché l’ippocampo ha una capacità limitata.

In una rete di memoria esiste un input per la rete, $x$ (si può pensare ad un indirizzo della memoria) che viene confrontato con i vettori $k_1, k_2, k_3, \cdots$ (“chiavi”) attraverso un prodotto scalare. Dandoli in ingresso ad un softmax si ottiene una matrice di numeri a somma uno. Ci sono poi una serie di altri vettori $v_1, v_2, v_3, \cdots$ (“valori”). Moltiplicando questi vettori per degli scalari ottenuti dai softmax e sommando i vettori così ottenuti (notare la somiglianza con il meccanismo di attenzione) si ottiene il risultato.

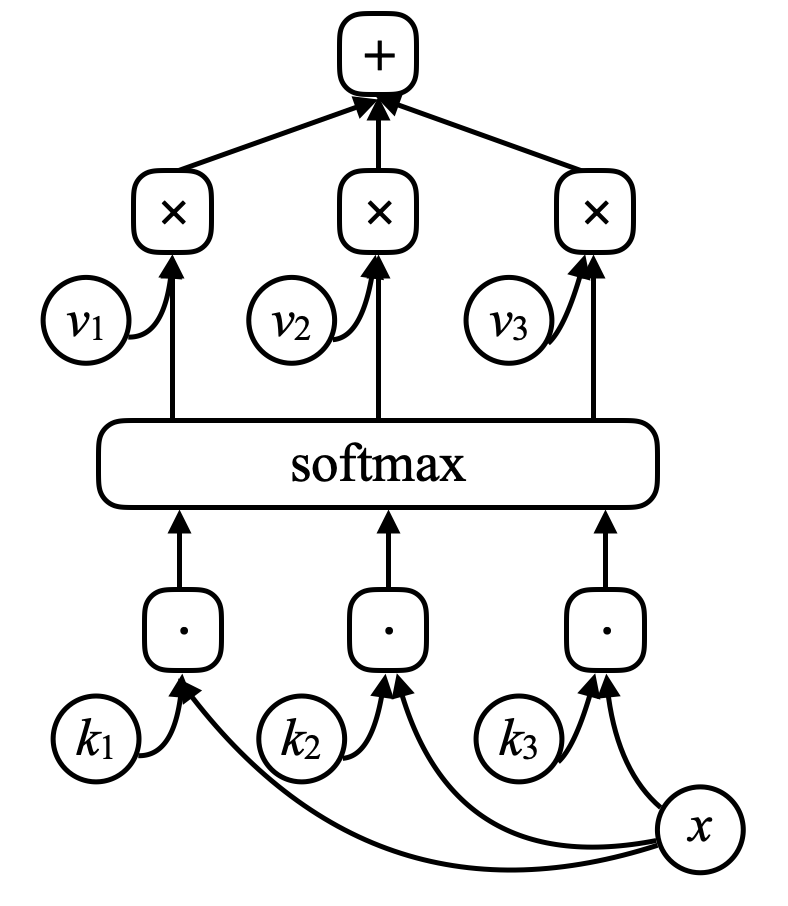
Figura 7. Reti di memoria

Se una delle chiavi (ad esempio $k_i$) corrisponde esattamente a $x$, il coefficiente associato a questa chiave sarà molto vicino a uno. Quindi l’output del sistema sarà essenzialmente $v_i$.

Questa è memoria associativa indirizzabile. Ovvero una memoria in cui ad ogni chiave corrisponde quello specifico valore. E questa è solo una versione leggermente differenziabile, che ti consente di fare retropropagazione e quindi cambiare i vettori attraverso la discesa del gradiente.

Quello che gli autori hanno fatto è stato raccontare una storia a un sistema dandogli una sequenza di frasi. Le frasi vengono codificate in vettori facendole passare attraverso una rete neurale che non è stata preaddestrata. Le frasi vengono riportate in una memoria di questo tipo. Quando si pone una domanda al sistema, si codifica la domanda e la si inserisce come input di una rete neurale, la rete neurale produce un $x$ in memoria e la memoria restituisce un valore.

This value, together with the previous state of the network, is used to re-access the memory. And you train this entire network to produce an answer to your question. After extensive training, this model actually learns to store stories and answer questions.

Questo valore, insieme allo stato precedente della rete, viene utilizzato per accedere nuovamente alla memoria. Così viene addestrata l’intera rete per produrre una risposta alla tua domanda. Dopo un lungo addestramento, questo modello impara effettivamente a memorizzare storie e rispondere a domande.

\(\alpha_i = k_i^\top x \\ c = \text{softmax}(\alpha) \\ s = \sum_i c_i v_i\)

In una rete di memoria, esiste una rete neurale che accetta un input e quindi produce un indirizzo per la memoria, ritorna il valore alla rete, continua ad eseguire e alla fine produce un output. Questo è molto simile ad un computer poiché c’è una CPU e una memoria esterna dove leggere e scrivere.

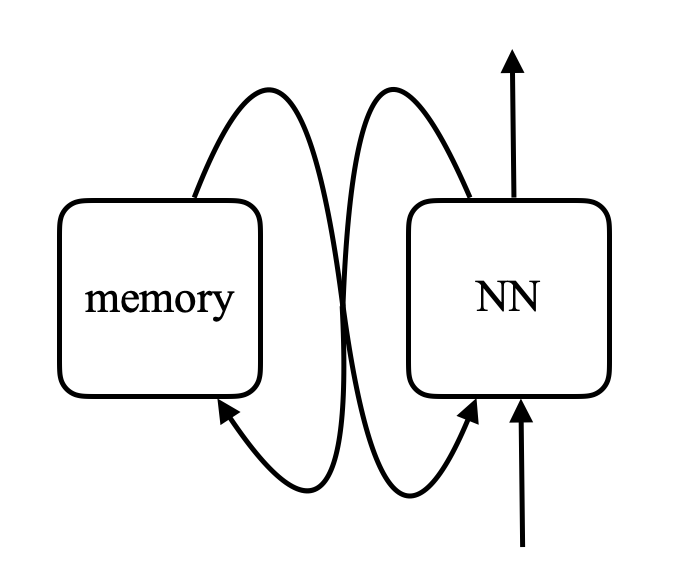
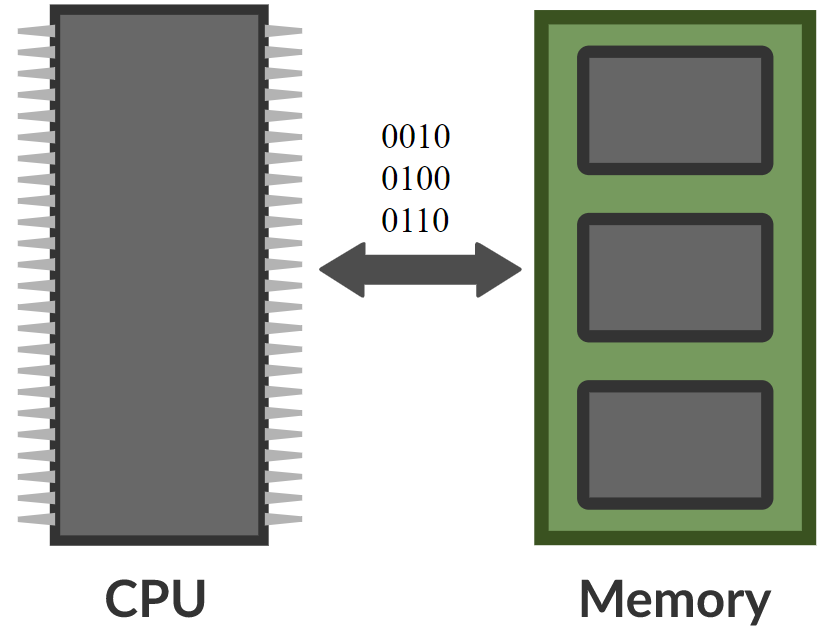
Figura 8. Confronto fra reti di memoria e computer (Foto da Khan Acadamy)

Ci sono persone che immaginano che tu possa effettivamente costruire computer differenziabili da questo tipo di modelli. Un esempio è la Neural Turing Machine di DeepMind, che è stata resa pubblica tre giorni dopo la pubblicazione dell’articolo di Facebook su arXiv.

L’idea è quella di confrontare gli input con le chiavi, generare coefficienti e produrre valori - che è fondamentalmente ciò che fa un modello trasformatore. Un trasformatore è fondamentalmente una rete neurale in cui ogni gruppo di neuroni è una di queste reti.