Applicazioni di Reti Convoluzionali

Riconoscimento di codici ZIP

Nella lezione precedente, abbiamo dimostrato come una rete convoluzionale sia in grado di riconoscere le cifre, tuttavia una questione rimane aperta: come fa il modello a selezionare ciascuna cifra ed evitare perturbazioni sulle cifre vicine? Il passaggio successivo consiste nel rilevare oggetti non sovrapposti e utilizzare l’approccio generale della soppressione dei non-massimi (non-maximum suppression, NMS). Supponendo che l’input sia una serie di cifre non sovrapposte, la strategia è quella di addestrare diverse reti convoluzionali ed utilizzare il voto di maggioranza oppure scegliere le cifre corrispondenti al punteggio più alto generato dalla rete convoluzionale.

Riconoscimento mediante CNN

Qui presentiamo il compito di riconoscere 5 codici postali non sovrapposti. Al sistema non sono state fornite istruzioni su come separare ogni cifra ma sa che è necessario predire 5 cifre. Il sistema (Figura 1) è costituito da 4 reti convoluzionali di dimensioni diverse, ciascuna delle quali produce un insieme di output. L’output è rappresentato da matrici. Le quattro matrici di output provengono da modelli con diverse larghezze del kernel nell’ultimo livello. In ogni output ci sono 10 righe che rappresentano le 10 categorie, da 0 a 9. Il quadrato bianco più grande rappresenta un punteggio più alto nella corrispondente categoria. In questi quattro blocchi di output, le dimensioni orizzontali del kernel degli ultimi layer sono rispettivamente 5, 4, 3 e 2. La dimensione del kernel decide la larghezza della finestra di visualizzazione del modello sull’input, pertanto ogni modello predice cifre basate su dimensioni della finestra diverse. Il modello quindi prende il voto di maggioranza e seleziona la categoria che corrisponde al punteggio più alto in quella finestra. Per estrarre informazioni utili, è necessario tenere presente che non tutte le combinazioni di caratteri sono possibili, pertanto correggere gli errori facendo leva sulle restrizioni sull’input è utile per garantire che gli output siano veri codici postali.

Figura 1: Diversi classificatori su riconoscimento di codici zip

Ora bisogna imporre l’ordine dei caratteri. Il trucco è utilizzare un algoritmo di cammino minimo. Poiché ci vengono forniti intervalli di caratteri possibili e il numero totale di cifre da prevedere, possiamo affrontare questo problema calcolando il costo minimo di generazione delle cifre e le transizioni tra le cifre. Il percorso deve essere continuo dalla cella in basso a sinistra sul grafico alla cella in alto a destra, e può contenere solo i movimenti da sinistra a destra e dal basso verso l’alto. Si noti che se lo stesso numero viene ripetuto, l’algoritmo dovrebbe essere in grado di distinguere che è in presenza di due numeri ripetuti invece di prevedere una singola cifra.

Riconoscimento facciale

Le reti neurali convoluzionali svolgono bene i compiti di rilevamento ed anche il rilevamento dei volti non fa eccezione. Per eseguire il rilevamento facciale, raccogliamo un set di dati di immagini con e senza volti, su cui addestriamo una rete convoluzionale (con una dimensione della finestra di circa 30 $\times$ 30 pixel) la quale ha il compito di rilevare la presenza di un volto. Una volta addestrata, applichiamo il modello a una nuova immagine e se ci sono facce approssimativamente all’interno di una finestra di 30 $\times$ 30 pixel, la rete convoluzionale illuminerà l’output nelle posizioni corrispondenti. Esistono tuttavia due problemi.

• Falsi positivi: ci sono molti modi in cui un oggetto che non è un volto possa apparire in una parte di immagine. Durante la fase di addestramento, il modello potrebbe non vederne tutte le varianti (ovvero, potrebbe non vedere un set completamente rappresentativo di immagini non contenente un volto). Pertanto, il modello potrebbe soffrire di molti falsi positivi durante la fase di test. Ad esempio, se il modello non è stato addestrato su immagini contenenti una mano, potrebbe rilevare un volto in base alla tonalità di pelle e scambierebbe una mano per un volto, risultando in falsi positivi.

• Diverse dimensioni del viso: Non tutti i volti sono 30 $\times$ 30 pixel, quindi i volti di dimensioni diverse potrebbero non essere rilevati. Un modo per gestire questo problema è generare più versioni della stessa immagine su diverse scale. Il rilevatore originale rileverà volti di circa 30 $\times$ 30 pixel. Se si riscala l’immagine di un fattore $\sqrt 2$, il modello rileverà volti più piccoli nell’immagine originale poiché ciò che era 30 $\times$ 30 è ora diventato 20 $\times$ 20 pixel all’incirca. Per rilevare volti più grandi, possiamo rimpicciolire l’immagine. Questo processo è economico poiché metà del costo deriva dall’elaborazione dell’immagine originale non in scala. La somma dei costi di tutte le altre reti combinate è quasi uguale all’elaborazione dell’immagine originale non ridimensionata. La dimensione della rete è il quadrato della dimensione dell’immagine su un lato, quindi se riduci l’immagine di $\sqrt 2$, la rete che devi eseguire è più piccola di un fattore di 2. Quindi il costo complessivo è $1+1/2+1/4+1/8+1/16+…$, che è 2. Da cui segue che il costo d’esecuzione di un modello multiscala è solamente il doppio di quello normale.

Un sistema di rilevamento facciale multiscala

Figura 2: Sistema di rilevamento facciale

Le mappe mostrate in (Figura 3) indicano i punteggi dei rilevatori di volti. Questo rilevatore di volti riconosce volti di dimensioni 20 $\times $ 20 pixel. In scala fine (Scala 3) ci sono molti punteggi alti ma non sono molto definiti. Quando il fattore di ridimensionamento aumenta (Scala 6), vediamo più aree bianche raggruppate. Quelle regioni bianche rappresentano i volti rilevati. Quindi applichiamo la soppressione dei non-massimi per ottenere la posizione finale del viso.

Figura 3: Punteggi dei rilevatori di volti per diversi fattori di scala

Soppressione dei non-massimi

In ogni regione con punteggio elevato vi è probabilmente sotto una faccia. Se vengono rilevati più volti molto vicini al primo, significa che solo uno dovrebbe essere considerato corretto e il resto sbagliato. Con la soppressione dei non-massimi, prendiamo il punteggio più alto tra le bounding boxes sovrapposte e rimuoviamo gli altri. Il risultato sarà una unica bounding box nella posizione ottimale.

Estrazione negativa

Nell’ultima sezione, abbiamo discusso di come il modello si possa imbattere in un numero elevato di falsi positivi al momento del test poiché ci sono molti modi per far apparire un oggetto che non è una faccia. Nessun set di addestramento potrà mai includere tutti gli oggetti che sembrano volti ma non lo sono. Possiamo mitigare questo problema attraverso il mining negativo. Nel mining negativo, creiamo un set di dati negativi formato da pezzi (patches) di immagine che non contengono volti che il modello rileva erroneamente come facce. I dati vengono raccolti eseguendo il modello su input noti per non contenere volti. Quindi addestriamo nuovamente il rivelatore utilizzando il set di dati negativi. Possiamo ripetere questo processo per aumentare la solidità del nostro modello contro i falsi positivi.

Segmentazione semantica

La segmentazione semantica è il compito di assegnare una categoria a ciascun pixel di un’immagine di input.

CNN per visione robotica adattiva a lungo raggio

In questo progetto, l’obiettivo era etichettare le regioni delle immagini di input in modo che un robot potesse distinguere tra strade e ostacoli. Nella figura, le regioni verdi sono aree su cui il robot può guidare e le regioni rosse sono ostacoli, come ad esempio l’erba alta. Per addestrare la rete per questa attività, abbiamo preso una patch dall’immagine ed l’abbiamo manualmente etichettata come attraversabile o meno (rispettivamente, verde o rosso). Addestriamo quindi la rete convoluzionale sui pezzi di immagine (patch) chiedendole di prevederne il colore. Una volta che il sistema sia stato sufficientemente addestrato, viene applicato all’intera immagine, etichettando tutte le regioni dell’immagine come verdi o rosse.

Figura 4:CNN per visione robotica adattiva a lungo raggio (programma DARPA LAGR 2005-2008)

Esistono cinque categorie da classificare: 1) verde intenso, 2) verde, 3) viola: linea del piede ostacolo, 4) rosso: ostacolo 5) rosso intenso: sicuramente un ostacolo.

Etichette stereo (Figura 4, Colonna 2) Le immagini vengono catturate dalle 4 telecamere sul robot e poi raggruppate in 2 coppie di visione stereo.Utilizzando le distanze note tra le telecamere della coppia stereo possiamo stimare le posizioni di ogni pixel nello spazio 3D; quest’ultime possono infatti essere calcolate misurando le distanze relative tra i pixel che appaiono in entrambe le telecamere in una coppia stereo. Questo è lo stesso processo che i nostri cervelli usano per stimare la distanza degli oggetti che vediamo. Utilizzando le informazioni sulla posizione stimata, si esegue il fitting di una superficie piana al terreno ed i pixel vengono quindi etichettati come verdi se si trovano vicino al suolo e rossi se si trovano sopra di esso.

• Motivazione per l’utilizzo delle ConvNet e le loro limitazioni: la visione stereo funziona solo fino a 10 metri e la guida di un robot richiede una visione a lungo raggio. Una ConvNet, invece, è in grado di rilevare oggetti a distanze molto maggiori se addestrata correttamente.

Figura 5: Piramide invariante per scala di immagini normalizzate sulla distanza

• Usata come input del modello: un’importante pre-elaborazione include la costruzione di una piramide a scala invariante di immagini normalizzate sulla distanza (Figura 5). È simile a quello che abbiamo fatto prima di questa lezione quando abbiamo cercato di rilevare i volti di più dimensioni.

Output del modello (Figura 4, colonna 3)

Il modello genera un’etichetta per ogni pixel dell’immagine fino all’orizzonte. Queste sono gli output di classificazione di una rete convoluzionale multiscala.

• Come il modello diventa adattivo: i robot hanno accesso continuo alle etichette stereo, permettendo alla rete di riaddestrarsi, adattandosi al nuovo ambiente in cui si trova. Si noti che solo l’ultimo strato della rete verrebbe riaddestrato in base all’ambiente. I livelli precedenti vengono addestrati in laboratorio e mantenuti costanti.

Prestazioni del sistema

Quando cercava di raggiungere una coordinata GPS dall’altra parte di una barriera, il robot “vedeva” la barriera da molto lontano e pianificava un percorso che la evitava. Questo avviene grazie alla CNN che rileva oggetti a 50-100m di distanza.

Limitazioni

Negli anni 2000, le risorse di calcolo erano limitate. Il robot era in grado di elaborare circa 1 fotogramma (frame) al secondo, il che significa che non sarebbe stato in grado di rilevare una persona che lo incrociava per un intero secondo prima di essere in grado di reagire. La soluzione per questa limitazione è un modello di odometria visiva a basso costo. Non si basa su reti neurali, ha una visione di ~2,5m ma reagisce rapidamente.

Analisi ed etichettatura delle scene

In questa attività, il modello genera una categoria di oggetti (edifici, automobili, cielo, ecc.) per ogni pixel. L’architettura è anche multi-scala (Figura 6).

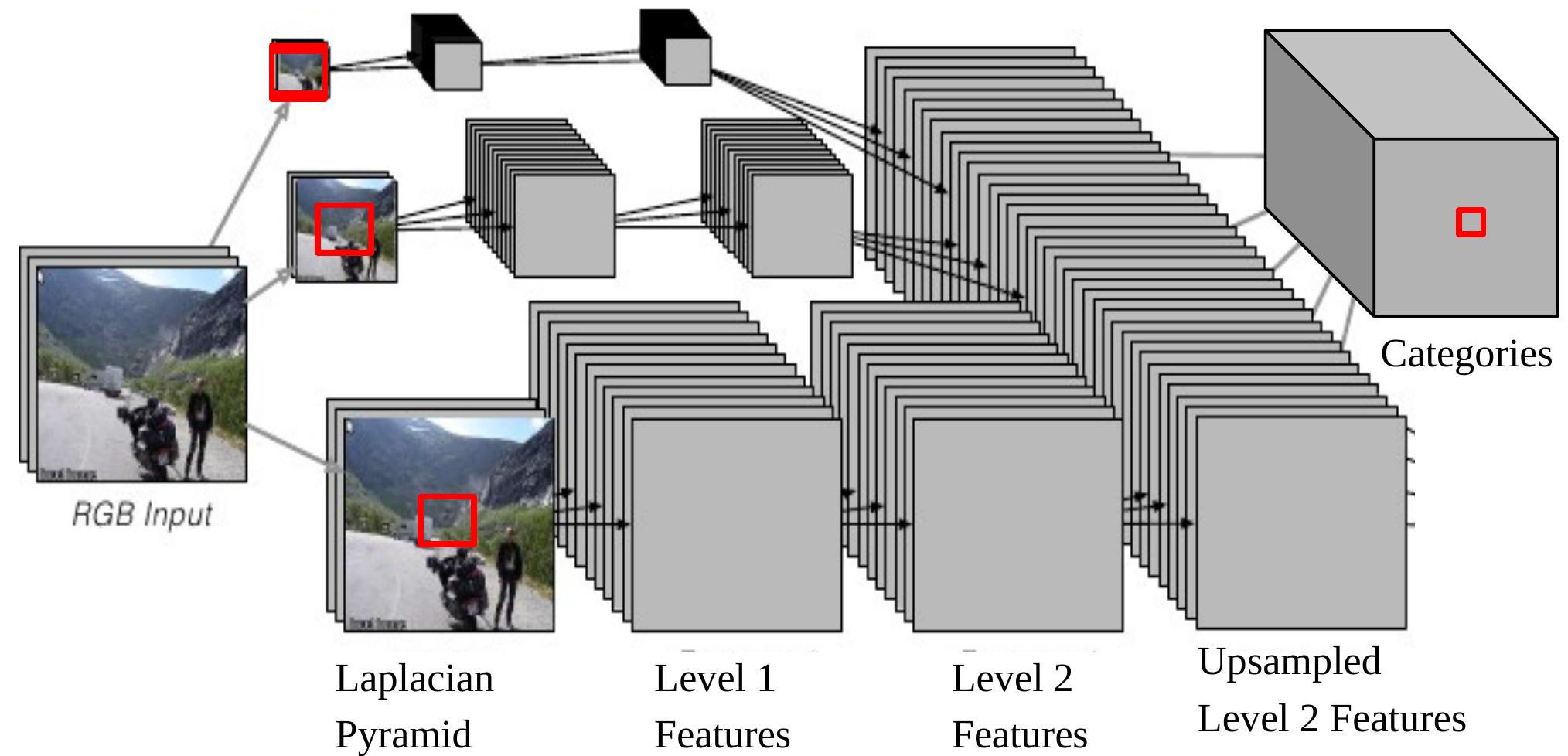
Figura 6: CNN multi-scala per l'analisi di scene

Si noti che se si proietta indietro un output della CNN sull’input, questo corrisponde a una finestra di input di dimensioni $46 \times 46$ sull’immagine originale nella parte inferiore della Piramide Laplaciana. Significa che stiamo usando il contesto di $46 \times 46$ pixel per decidere la categoria del pixel centrale.

Tuttavia, a volte questa dimensione del contesto non è sufficiente per determinare la categoria di oggetti più grandi.

L’approccio multiscala consente una visione più ampia fornendo ulteriori immagini ridimensionate come input. I passaggi sono i seguenti:

1. Prendi la stessa immagine, riducila di un fattore 2 e di un fattore 4, separatamente.
2. Queste due immagini extra che sono state ridimensionate vengono inviate alla stessa ConvNet (stessi pesi, stessi kernel) e otteniamo altri due set di caratteristiche (features) di Livello 2.
3. Sovracampionamento di queste caratteristiche in modo che abbiano le stesse dimensioni delle caratteristiche di livello 2 dell’immagine originale.
4. Impila le tre serie di caratteristiche (ricampionate) insieme e utilizzarle come input ad un classificatore.

Ora la più grande dimensione effettiva del contenuto, che deriva dall’immagine 1/4 ridimensionata, è $184 \times 184$, ($46 \times 4 = 184$).

Prestazioni: senza post-elaborazione ed eseguendolo fotogramma per fotogramma (frame-by-frame), il modello funziona molto velocemente anche su hardware standard. Ha una dimensione piuttosto piccola di dati di allenamento (2k~3k), ma i risultati sono ancora da record.