Comprendere le convoluzioni e i meccanismi di differenziazione automatica

Comprendere una convoluzione monodimensionale

In questa parte discuteremo delle convoluzioni, giacché vogliamo esplorare la sparsità, la stazionarietà e la composizionalità dei dati.

Anziché utilizzare la matrice $A$, come fatto nella settimana scorsa, cambieremo la larghezza della matrice con la dimensione del kernel $k$. Di conseguenza, ogni riga della matrice ora è interpretabile come un kernel. Possiamo utilizzare i kernel tramite accatastamento e traslazione (Fig. 1). Dunque avremo $m$ strati di altezza $n-k+1$.

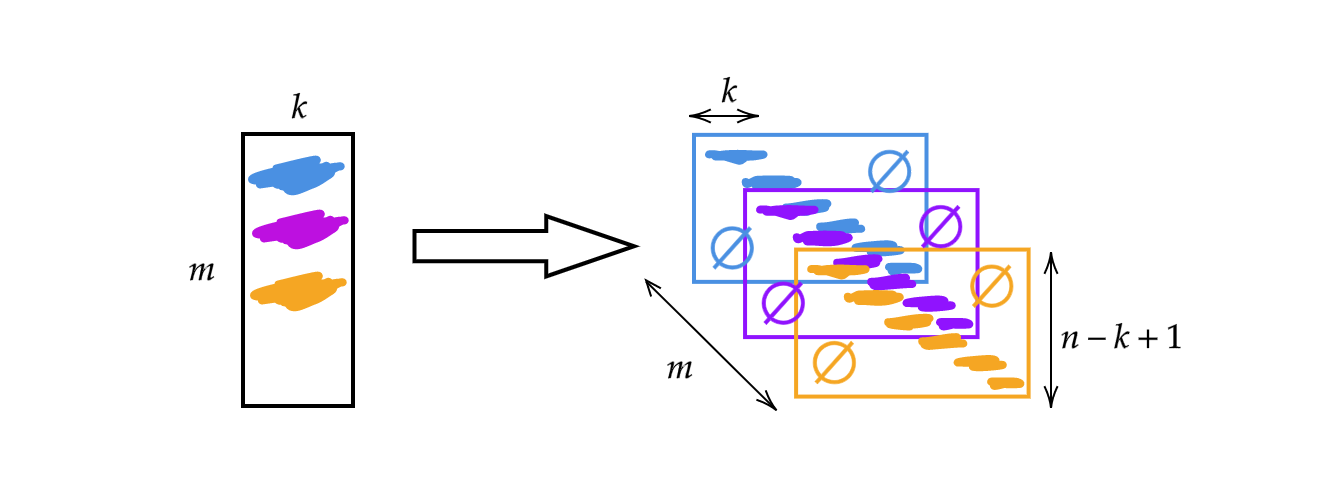
Fig. 1: illustrazione di una convoluzione monodimensionale

L’output corrisponde a $m$ (spessore) vettori di dimensione $n-k+1$.

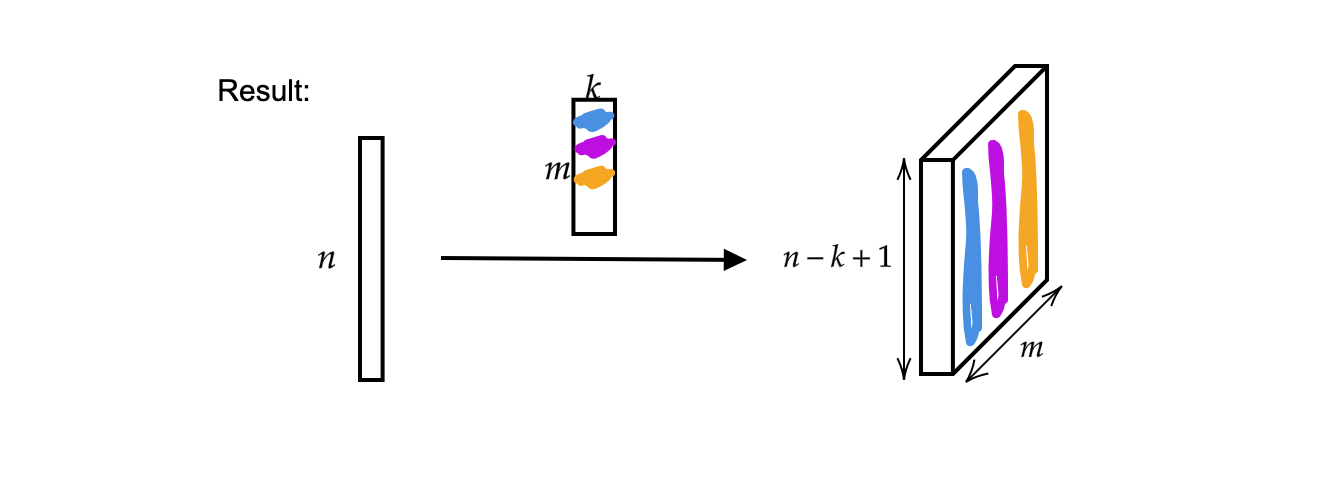
Fig. 2: risultato di una convoluzione monodimensionale

Inoltre, un singolo vettore di input può essere visto come un segnale monofonico.

Fig 3: un segnale monofonico

Ora, l’input $x$ è una mappatura

dove $\Omega = \lbrace 1, 2, 3, \cdots \rbrace \subset \mathbb{N}^1$ (poiché questo è un segnale monodimensionale, ha $1$ dominio dimensionale) e in questo caso il numero di canali $c$ è $1$. Quando $c = 2$, questo diventa un segnale stereofonico.

Per la convoluzione in 1D, possiamo solo computare il prodotto scalare kernel per kernel (Fig. 4).

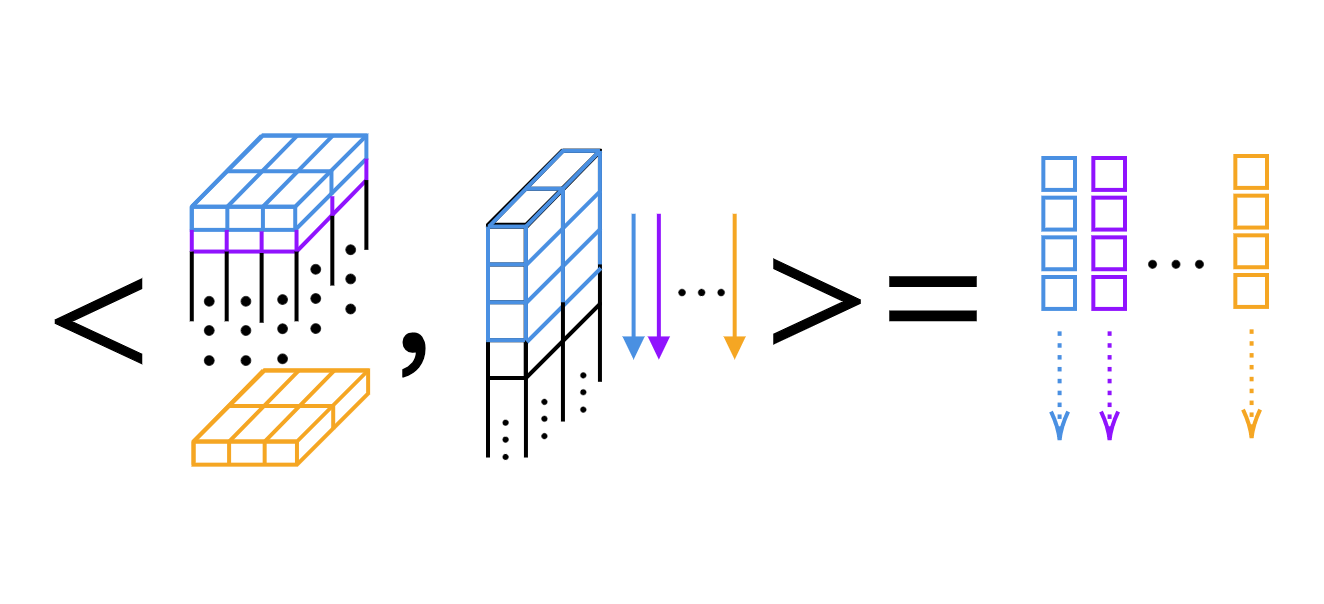
Fig 4: Prodotto scalare kernel per kernel di una convoluzione in 1D

Dimensione del kernel e larghezza dell’output in PyTorch

Suggerimento: Possiamo usare il punto di domanda in IPython per accedere alla documentazione delle funzioni. Ad esempio,

Init signature:
nn.Conv1d(
	in_channels,           # numero di canali dell'immagine di input
	out_channels,          # numero di canali prodotti dalla convoluzione
	kernel_size,           # dimensione del kernel convoluzionale
	stride=1,              # passo della convoluzione
	padding=0,             # padding ("imbottitura") di zeri in entrambi i lati dell'input
	dilation=1,            # spaziatura fra elementi del kernel
	groups=1,              # numero di connessioni raggruppate fra input e output
	bias=True,             # se `True`, aggiunge un bias addestrabile all'output
	padding_mode='zeros',  # accetta valori come `zeros` e `circular`
)

Convoluzione 1D

Abbiamo una convoluzione $1$-dimensionale applicata ad un segnale a $2$ canali (segnale stereofonico) a $16$ canali ($16$ kernel) con kernel di dimensione $3$ e passo $1$. Successivamente, abbiamo $16$ kernel di spessore $2$ e lunghezza $3$. Assumiamo che il segnale di input abbia una dimensione del batch pari a $1$ (un segnale), $2$ canali e $64$ istanze. Il risultante strato di output ha $1$ segnale, $16$ canali e la lunghezza del segnale è pari a $62$ ($=64-3+1$). Inoltre, se consideriamo la grandezza del bias, scopriamo che essa è $16$, dal momento che abbiamo un bias per peso.

conv = nn.Conv1d(2, 16, 3)  # 2 canali (segnale stereo), 16 kernel di dimensione 3
conv.weight.size()          # output: torch.Size([16, 2, 3])
conv.bias.size()            # output: torch.Size([16])

x = torch.rand(1, 2, 64)    # batch di dimensione 1, 2 canali, 64 istanze
conv(x).size()              # output: torch.Size([1, 16, 62])

conv = nn.Conv1d(2, 16, 5)  # 2 canali, 16 kernel di dimensione 5
conv(x).size()              # output: torch.Size([1, 16, 60])

Convoluzione 2D

Prima di tutto, chiariamo che il dato di input sia $1$ immagine composta da $20$ canali (assumiamo sia un’immagine iperspettrale) con altezza $64$ e larghezza $128$. La convoluzione 2D ha $20$ canali di input e $16$ kernel di dimensione $3 \times 5$. Dopo la convoluzione, l’output rimane $1$ immagine composta da $16$ canali di altezza $62$ $(=64-3+1)$ e larghezza $124$ ($=128-5+1$).

x = torch.rand(1, 20, 64, 128)    # 1 istanza, 20 canali, altezza 64, e larghezza 128
conv = nn.Conv2d(20, 16, (3, 5))  # 20 canali, 16 kernel, dimensione del kernel 3 x 5
conv.weight.size()                # output: torch.Size([16, 20, 3, 5])
conv(x).size()                    # output: torch.Size([1, 16, 62, 124])

Se volessimo ottenere la stessa dimensionalità, dovremmo introdurre del padding. Prendendo come riferimento il codice qui sopra, possiamo aggiungere nuovi parametri alla funzione di convoluzione: stride=1 e padding=(1,2), ovvero padding di $1$ pixel nella direzione $y$ ($1$ sopra l’immagine, $1$ di sotto) e $2$ nella direzione $x$. Dopodiché, il segnale di output ha la stessa dimensione rispetto all’input. Il numero di dimensioni da conservare per l’insieme dei kernel per una convoluzione 2D è $4$.

# 20 canali, 16 kernel di dimensione 3 x 5, passo di 1, padding di 1 e 2
conv = nn.Conv2d(20, 16, (3, 5), 1, (1, 2))
conv(x).size()  # output: torch.Size([1, 16, 64, 128])

Come funziona il gradiente automatico?

In questa sezione andremo a chiedere a torch di verificare tutte le computazioni sui tensori così che possiamo ottenere i calcoli delle derivate parziali.

• Creare un tensore $\boldsymbol{x}$ di dimensione $2 \times 2$ con proprietà di accumulazione del gradiente;
• Sottrarre $2$ da tutti gli elementi di $\boldsymbol{x}$ ottenendo $\boldsymbol{y}$; (se stampiamo y.grad_fn, otteniamo <SubBackward0 object at 0x12904b290>, il che significa che y è generato dal modulo della sottrazione $\boldsymbol{x}-2$. Possiamo anche utilizzare y.grad_fn.next_functions[0][0].variable per ri-ottenere il tensore originale);
• Facciamo ancora un’operazione: $\boldsymbol{z} = 3\boldsymbol{y}^2$;
• Calcoliamo la media di $\boldsymbol{z}$

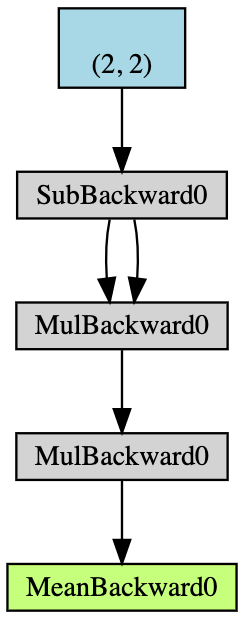
Fig. 5: Diagramma di flusso dell'esempio di calcolo automatico del gradiente

La retropropagazione è usata per computare i gradienti. In questo esempio, il processo di retropropagazione può essere visto come una computazione del gradiente $\frac{d\boldsymbol{a}}{d\boldsymbol{x}}$. Dopo aver calcolato a mano $\frac{d\boldsymbol{a}}{d\boldsymbol{x}}$ a fini validativi, possiamo vedere che l’esecuzione di a.backward() ci dà lo stesso valore di x.grad del nostro calcolo.

Di seguito il processo di computazione della retropropagazione a mano:

Quandunque si utilizzi una derivata parziale in PyTorch, si ottiene la stessa dimensione dei dati originali. Ma lo jacobiano corretto dovrebbe essere il trasposto di quanto ottenuto.

Verso cose più complicate

Ora abbiamo un vettore $x$ di dimensione $1 \times 3$, assegniamo a $y$ il doppio di $x$ e raddoppiamo $y$ fintantoché la sua norma è inferiore a $1000$. A causa dell’aleatorietà di $x$, non possiamo direttamente sapere il numero di iterazioni in cui la procedura sarà completata.

x = torch.randn(3, requires_grad=True)

y = x * 2
i = 0
while y.data.norm() < 1000:
    y = y * 2
    i += 1

Tuttavia, possiamo facilmente inferirlo conoscendo il gradiente

gradients = torch.FloatTensor([0.1, 1.0, 0.0001])
y.backward(gradients)

print(x.grad)
tensor([1.0240e+02, 1.0240e+03, 1.0240e-01])
print(i)
9

Per l’inferenza, possiamo utilizzare requires_grad=True per evidenziare che vogliamo tenere traccia dell’accumulazione del gradiente, come mostrato di sotto. Se omettiamo requires_grad=True nella dichiarazione di $x$ o $w$ e chiamiamo backward() su $z$, ci sarà un errore di runtime, giacché non c’è accumulazione del gradiente su $x$ oppure $w$.

# Sia x che w supportano l'accumulazione del gradiente
x = torch.arange(1., n + 1, requires_grad=True)
w = torch.ones(n, requires_grad=True)
z = w @ x
z.backward()
print(x.grad, w.grad, sep='\n')

Inoltre, possiamo specificare with torch.no_grad() per omettere l’accumulazione del gradiente.

x = torch.arange(1., n + 1)
w = torch.ones(n, requires_grad=True)

# Non vi sarà accumulazione del gradiente sui tensori
with torch.no_grad():
    z = w @ x

try:
    z.backward()  # PyTorch darà errore qui, visto che z non permette accumulo del gradiente
except RuntimeError as e:
    print('RuntimeError!!! >:[')
    print(e)

Materiale aggiuntivo – gradienti personalizzati

Inoltre, invece di operazioni numeriche basilari, possiamo generare il nostro modulo o la nostra funzione da noi definiti, da inserire nel grafo neurale. Il Jupyter Notebook corrispondente può essere trovato qui.

Per fare ciò, dobbiamo ereditare torch.autograd.Function e sovraccaricare le funzioni forward() e backward(). Per esempio, se vogliamo addestrare reti neurali, dobbiamo effettuare il passaggio in avanti e conoscere le derivate parziali dell’input nei confronti dell’output, in modo tale da utilizzare questo modulo in ogni punto del codice. Quindi, usando la retropropagazione (regola della derivazione delle funzioni composte), possiamo riprende il modulo ed utilizzarlo ovunque sia necessario nella catena di operazioni, fintantoché sappiamo calcolare le derivate parziali dell’input sull’output.

In questo caso, ci sono tre esempi di modulo personalizzato nel notebook, add, split e max. Per esempio, nel modulo personalizzato sull’addizione:

# Custom addition module
class MyAdd(torch.autograd.Function):

    @staticmethod
    def forward(ctx, x1, x2):
        # ctx è un contesto dove possiamo salvare
        # i calcoli per backward
        ctx.save_for_backward(x1, x2)
        return x1 + x2

    @staticmethod
    def backward(ctx, grad_output):
        x1, x2 = ctx.saved_tensors
        grad_x1 = grad_output * torch.ones_like(x1)
        grad_x2 = grad_output * torch.ones_like(x2)
        # dobbiamo restituire i gradienti nell'ordine
		# dell'input verso avanti (escludendo ctx)
        return grad_x1, grad_x2

Se abbiamo un’addizione di due oggetti e otteniamo un output, dobbiamo sovrascrivere la funzione forward come fatto sopra. E quando facciamo la retropropagazione, dobbiamo copiare il gradiente da entrambe le direzioni. In questo modo sovrascriviamo la funzione backward tramite copiatura.

Per split e max, si faccia riferimento al notebook per il codice su come sovrascrivere le funzioni forward e backward. Se utilizziamo Split, nella retropropagazione dovremmo sommare i gradienti. Per argmax, viene selezionato l’indice dell’oggetto maggiore, così il gradiente tale indice dovrebbe essere valorizzato a $1$ mentre tutti gli altri a $0$. Si ricordi che, per ogni modulo personalizzato, dobbiamo sovrascrivere il passaggio in avanti e, nella funzione backward, il modo con il quale si calcolano i gradienti.