Tecniche di ottimizzazione II

Metodi adattivi

L’SGD con momento rappresenta attualmente lo stato dell’arte dei metodi di ottimizzazione per molti problemi di ML. Ma ci sono altri metodi, generalmente chiamati adattivi, innovati nel corso degli anni, particolarmente utili per problemi mal condizionati (nel caso in cui SGD non funzioni).

Nella formulazione di SGD, ogni singolo peso della rete è aggiornato utilizzando un’equazione con lo stesso livello di apprendimento ($\gamma$ globale). Qui, per metodi adattivi intendiamo che adattiamo il livello di apprendimento individualmente per ogni peso. Per questo scopo, è utilizzata l’informazione fornitaci dai gradienti per ogni peso.

Le reti più frequentemente utilizzate hanno diverse strutture in diverse parti di esse. Per esempio, la prima frazione di una CNN può essere molto spesso composta da strati convoluzionali su immagini grandi, mentre più in fondo alla rete possiamo avere convoluzioni di un gran numero di canali su immagini piccole. Queste due opreazioni sono molto diverse, cosicché un livello di apprendimento che funzioni bene per la prima parte della rete potrebbe non andare bene per le sezioni finali. Ciò implica i livelli di apprendimento adattivi potrebbero essere di una certa utilità.

I pesi nella parte finale della rete (4096 nella Fig. 1 di cui sotto) sfociano direttamente nell’output e hanno un forte effetto su quest’ultimo. Di conseguenza, necessitiamo di un livello di apprendimento più basso per loro. D’altro canto, i pesi degli strati iniziali hanno un effetto individuale più limitato sull’output, specialmente quando inizializzati in maniera casuale.

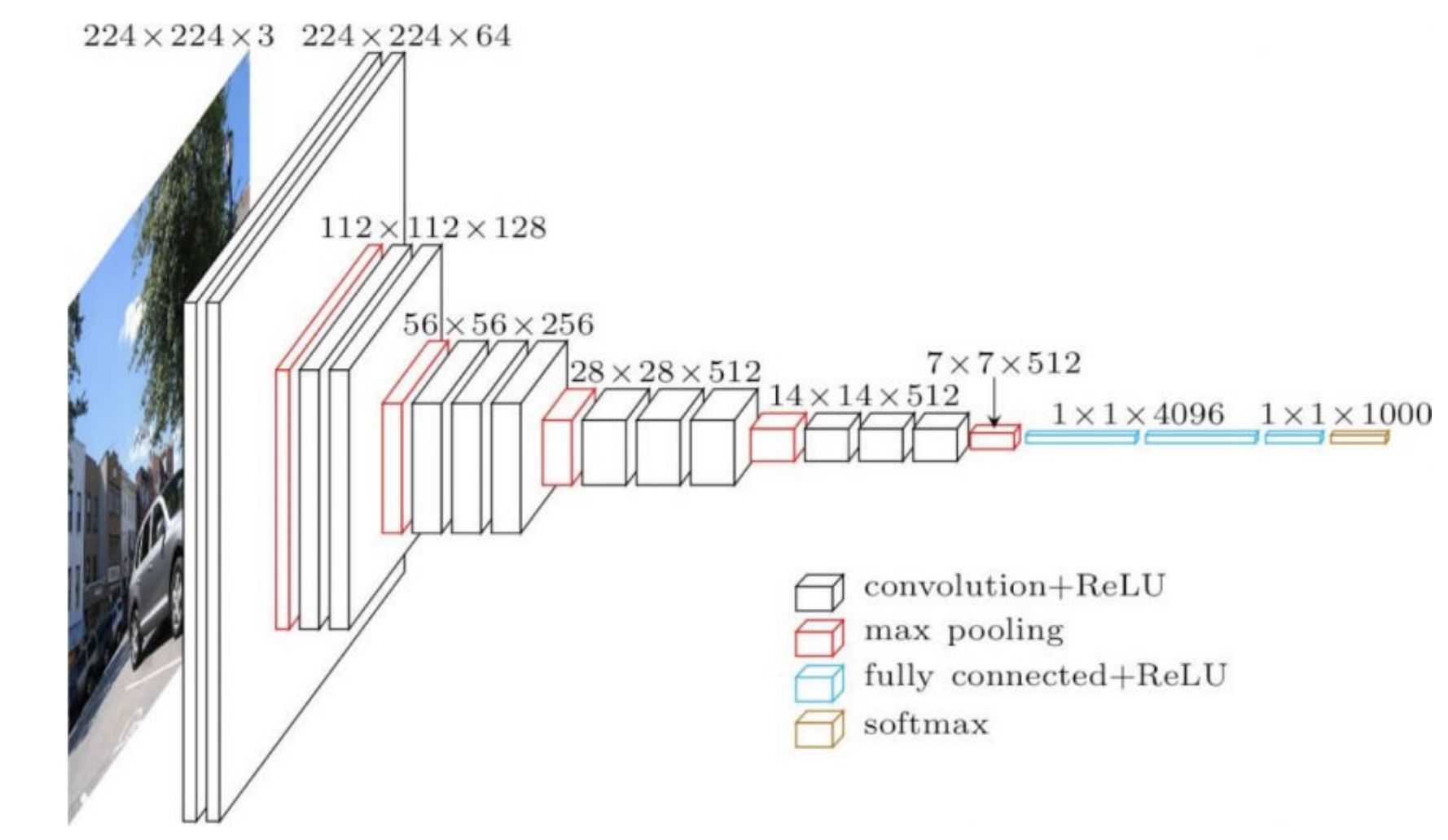
Fig. 1: la CNN VGG16

RMSprop

L’intuizione dietro a RMSprop (acronimo di Root Mean Square Propagation) è che il gradiente viene normalizzato attraverso la radice della media quadratica di quest’ultimo.

Nell’equazione di cui sotto, l’elevazione a quadrato del gradiente viene effettuata individualmente per ogni elemento del vettore.

dove $\gamma$ è il livello di apprendimento globale, $\epsilon$ è una costante molto piccola (dell’ordine di $10^{-7}$ o $10^{-8}$) utilizzata al fine di evitare errori di divisione per 0 e $v_{t+1}$ è una stima del secondo momento.

Aggiorniamo $v$ al fine di stimare una quantità rumorosa tramite una media mobile esponenziale (un metodo standard per mantenere una media di una quantità che può cambiare con il tempo). Abbiamo bisogno di dare più peso ai valori più recenti in quanto apportano più informazione. Un modo per fare ciò è smorzare in maniera esponenziale i valori meno recenti. Nel calcolo di $v$, i valori più vecchi vengono ridotti di un fattore costante $\alpha \in (0;1)$ ad ogni passo. Questo smorza i valori meno recenti finché non sono più una parte importante della media mobile esponenziale.

Il metodo originario tiene una media mobile esponenziale del secondo momento non centrato, cosicché non serve che sottraiamo la media in questo caso. Il secondo momento è usato per normalizzare il gradiente elemento per elemento, ovvero, ogni elemento del gradiente viene diviso per la radice della stima del secondo momento. Se il valore atteso del gradiente è piccolo, questo processo è simile alla divisione del gradiente per la sua deviazione standard.

Utilizzando un $\epsilon$ piccolo al denominatore non si causano divergenze, in quanto, quando $v$ è molto piccolo, anche il momento è molto piccolo di conseguenza.

ADAM

ADAM, acronimo di ADAptive Moment estimation, un RMSprop con l’aggiunta del momento, è un metodo più spesso utilizzato. L’aggiornamento del momento è convertito in una media mobile esponenziale e non è necessario cambiare il livello di apprendimento quando abbiamo a che fare con $\beta$. Come in RMSprop, calcoliamo una media mobile esponenziale del gradiente al quadrato.

dove $m_{t+1}$ è la media mobile esponenziale del momento.

Esiste anche una forma di correzione della distorsione della media mobile nel corso delle iterazioni, ma essa non è indicata in questa formula.

Considerazioni pratiche

Quando addestriamo reti neurali, SGD spesso prende una direzione sbagliata all’inizio del processo di addestramento, laddove RMSprop invece punta verso la direzione corretta. Comunque, RMSprop induce rumore così come l’SGD classico, e rimbalza attorno all’ottimo in maniera significativa quando si avvicina ad esso. Così come aggiungiamo il momento a SGD, otteniamo lo stesso miglioramento con ADAM. È un buono stimatore poco rumoroso della soluzione, cosicché ADAM è genericamente raccomandato al posto di RMSprop.

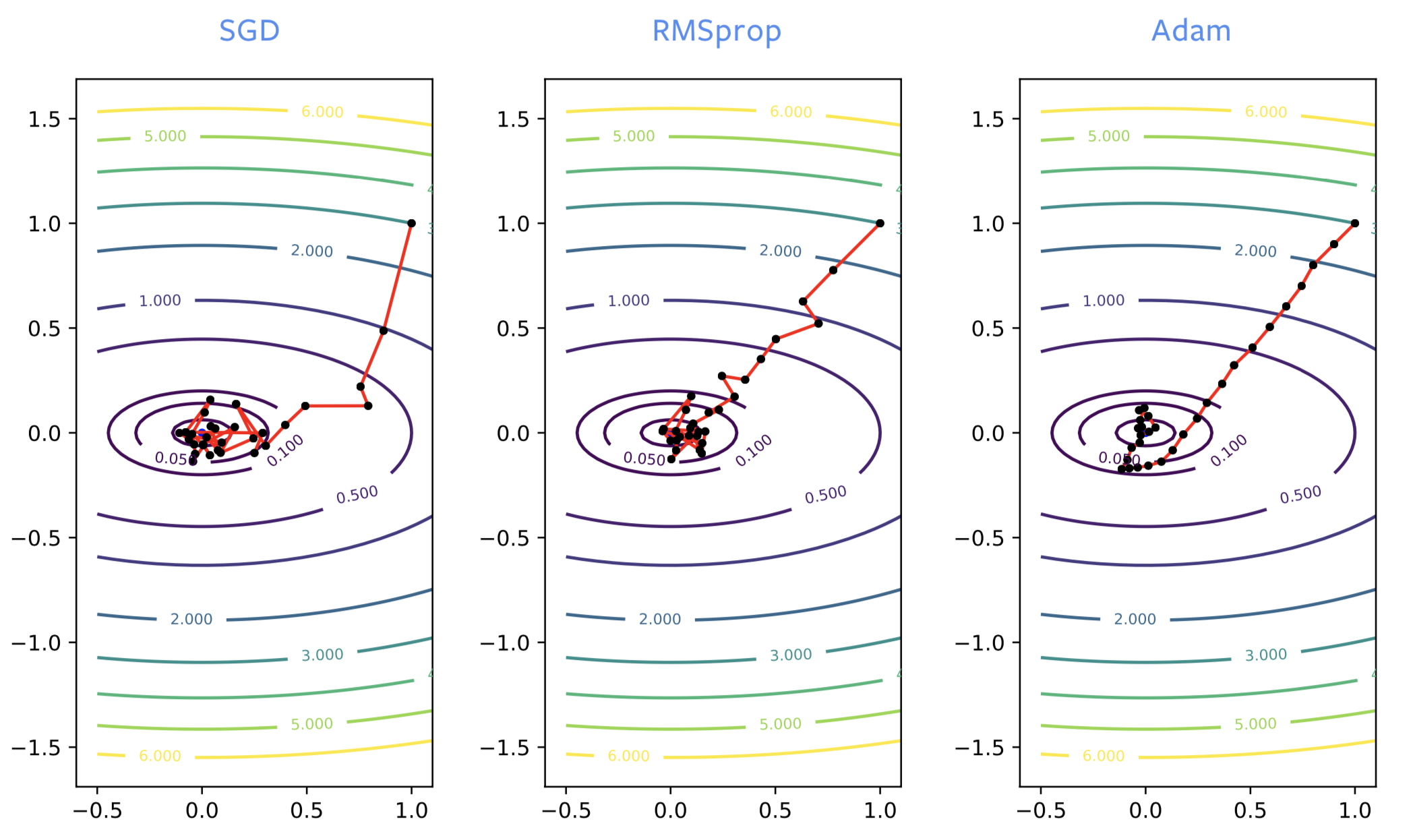
Fig. 2: SGD vs RMSprop vs ADAM

ADAM è necessario per addestrare alcune delle reti per modelli di linguaggio. Per ottimizzare le reti neurali, SGD con momento o ADAM sono normalmente preferiti. Tuttavia, la teoria di ADAM, nelle pubblicazioni, è poco compresa; ha inoltre svariati svantaggi:

• si può mostrare che, su problemi molto semplici, il metodo non converge;
• è noto che il metodo introduca errori di generalizzazione. Se la rete neurale è addestrata affinché restituisca una perdita pari a zero sui dati di addestramento, non restituirà perdita zero su altri punti che non ha mai visto precedentemente. È molto comune, in particolar modo su problemi di visione, che si ottengono errori di generalizzazione peggiori rispetto a quanto avremmo ottenuto con SGD. Alcuni fattori che potrebbero causare ciò potrebbero essere, ad esempio: la tendenza a convergere verso minimi locali più vicini al punto di partenza, troppo poco rumore in ADAM, o la sua struttura;
• con ADAM manteniamo 3 buffer, laddove SGD ne necessita soltanto 2. Ciò non è di grossa importanza, a meno che non addestriamo un modello di grandezza dell’ordine di svariati gigabyte, il che potrebbe eccedere la memoria a disposizione;
• ci sono 2 parametri del momento da adeguare, anziché uno solo.

Strati di normalizzazione

Anziché migliorare gli algoritmi di ottimizzazione, gli strati di normalizzazione migliorano la struttura della rete. Sono strati ulteriori da inserire fra strati già esistenti. L’obiettivo è migliorare l’ottimizzazione e le performance per quanto riguarda la generalizzazione.

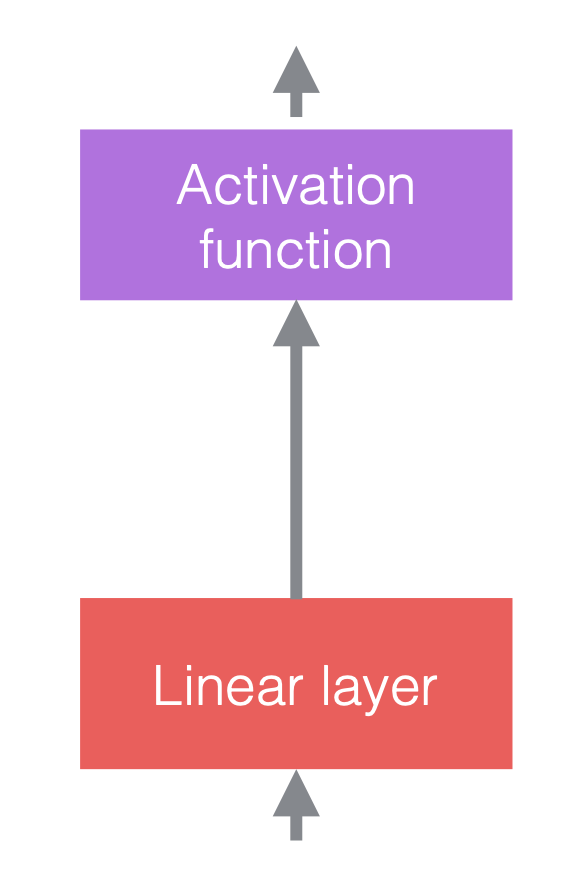
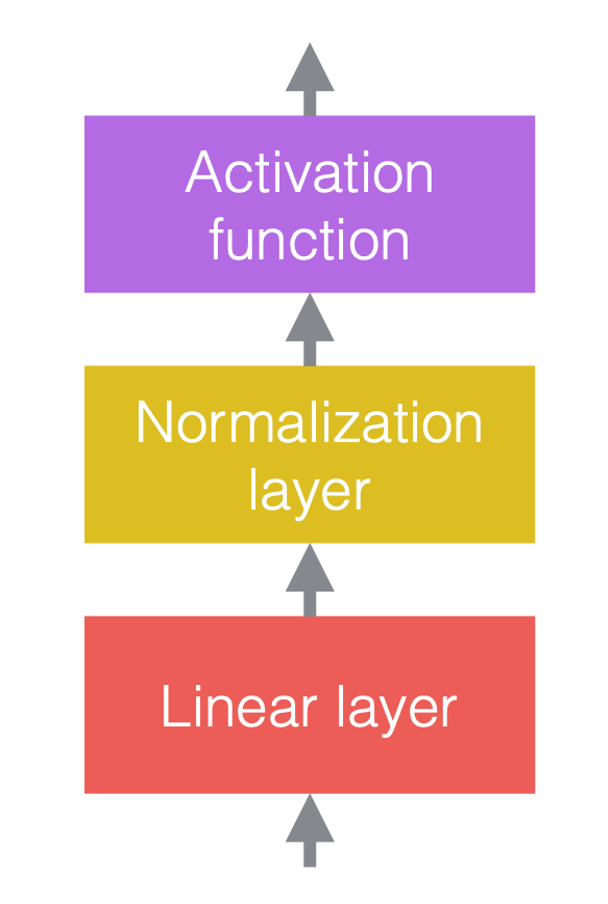
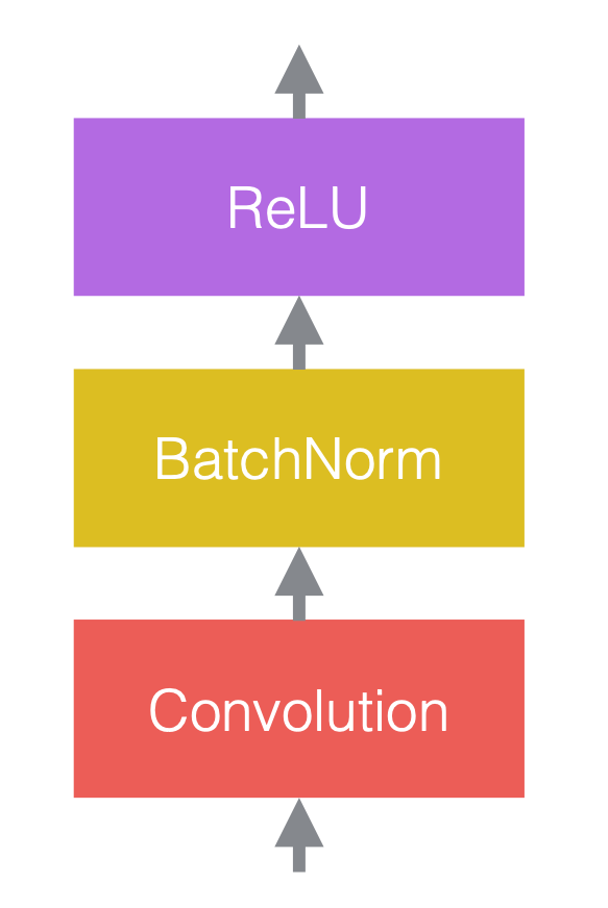
Nelle reti neurali, normalmente alterniamo operazioni lineari con operatori non lineari. Questi ultimi sono anche conosciuti come funzioni di attivazione, ad esempio ReLU. Possiamo posizionare strati di normalizzazione prima degli strati lineari o dopo le funzioni di attivazione. La pratica più comune è metterli prima degli strati lineari e delle funzioni di attivazione, come nella figura qui sotto.

(a) Prima dell’aggiunta di normalizzazione	(b) Dopo l’aggiunta della normalizzazione	(c) Un esempio nelle CNN

Nella Fig. 3(c), la convoluzione è lo strato lineare, seguita dalla normalizzazione del batch (“batch normalization” in inglese), seguita dalla ReLU.

Si noti che gli strati di normalizzazione influenzano i dati che ne passano attraverso, ma non variano la potenza della rete, nel senso che, con un’adeguata configurazione dei pesi, la rete non normalizzata è sempre in grado di fornire lo stesso output della rete normalizzata.

Operazioni di normalizzazione

Questa è la generica notazione della normalizzazione:

dove $x$ è un vettore di input, $y$ è il vettore di output, $\mu$ è la stima della media di $x$, $\sigma$ è la stima della media della deviazione standard (std) di $x$, $a$ è il fattore di scala e $b$ è il termine di distorsione. I valori di entrambi questi ultimi due termini si apprendono nel corso dell’addestramento.

Senza i parametri “addestrabili” $a$ e $b$, la distribuzione di output del vettore di output $y$ avrà media fissa 0 e std 1. Il fattore di scala $a$ e il termine di distorsione $b$ mantengono il potere di rappresentazione della rete, ovvero, i valori di output possono sempre variare all’interno di un qualsiasi range specifico. Si noti che $a$ e $b$ non invertono la normalizzazione, perché si possono imparare con l’addestramento e sono molto più stabili di $\mu$ e $\sigma$.

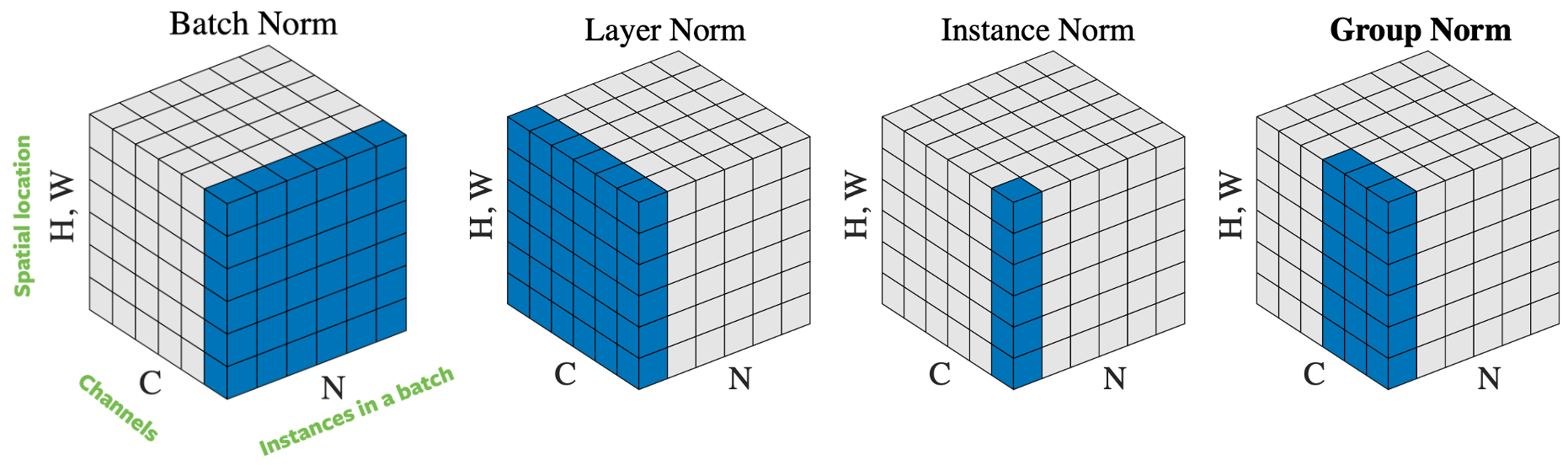
Fig. 4: Operatori di normalizzazione.

Ci sono svariati modi di normalizzare il vettore di input in base a come selezioniamo i campioni per la normalizzazione. In Fig. 4 vi sono quattro diversi approcci diverso alla normalizzazione, per un mini-batch di $N$ immagini di altezza $H$ e base $W$ e composte da $C$ canali:

• Normalizzazione del batch: la normalizzazione viene applicata su un solo canale dell’input. Questo è il primo approccio proposto e anche quello più conosciuto. Per approfondire, si legga How to Train Your ResNet 7: Batch Norm (in inglese);
• Normalizzazione dello strato: la normalizzazione viene applicata ad un’immagine contemporaneamente su tutti i suoi canali;
• Normalizzazione dell’istanza: la normalizzazione è applicata solamente su un’immagine e un canale;
• Normalizzazione di gruppo: la normalizzazione è applicata ad un’immagine su alcuni dei suoi canali. Ad esempio, i canali da 0 a 9 formano un gruppo, quelli da 10 a 19 ne formano un altro, e così via. In pratica, la dimensione di un gruppo è quasi sempre 32. Questo è l’approccio raccomandato da Aaron Defazio, in quanto mostra delle buone performance in pratica e non contrasta con SGD.

In pratica, sia la normalizzazione del batch che la normalizzazione di gruppo funzionano bene per problemi di visione artificiali, mentre la normalizzazione dello strato e dell’istanza sono usate in maniera massiccia per problemi di linguaggio.

Perché la normalizzazione aiuta l’addestramento?

Nonostante la normalizzazione funzioni bene in pratica, le ragioni dietro alla sua efficacia sono ancora dibattute. Originariamente, la normalizzazione viene proposta per ridurre la “variazione interna alle distribuzioni”, ma alcuni accademici hanno dimostrato che questo non accade in alcuni esperimenti. Nonostante ciò, la normalizzazione mostra chiaramente una combinazione dei seguenti fattori:

• le reti con strati di normalizzazione sono più facili da ottimizzare, permettendo l’impiego di livelli di apprendimento più alti. La normalizzazione ha un effetto di ottimizzazione che velocizza l’addestramento della rete neurale;
• gli stimatori di media e std sono rumorosi per effetto della casualità dei campioni del batch. Questo rumore aggiuntivo risulta in una miglior generalizzazione in alcuni casi. La normalizzazione ha anche un effetto di regolarizzazione;
• la normalizzazione riduce la sensibilità all’inizializzazione dei pesi.

Come risultato di ciò, la normalizzazione ci permette di essere più “sventati” – si possono combinare in maniera deliberata quasi tutti i mattoni, avendo comunque una buona chance di addestrarla senza dover effettuare considerazioni sullo scarso condizionamento del problema.

Considerazioni pratiche

È importante che la retropropagazione sia effettuata attraverso il calcolo della media e della std, così come l’applicazione della normalizzazione, altrimenti l’addestramento della rete porterà a divergenze. Il calcolo della retropropagazione è moderatamente complicato e soggetto a errori, ma PyTorch è in grado di computarlo automaticamente per noi, il che è molto utile. Le classi di strati di normalizzazione in PyTorch sono indicate qui sotto:

torch.nn.BatchNorm2d(num_features, ...)
torch.nn.GroupNorm(num_groups, num_channels, ...)

La normalizzazione del batch fu il primo metodo sviluppato ed è, ad oggi, il più conosciuto. Tuttavia, Aaron Defazio raccomanda, invece, l’utilizzo della normalizzazione di gruppo. È più stabile, più semplice da comprendere nella sua teoria e normalmente funziona meglio. Una dimensione dei gruppi pari a 32 è un buon valore di default.

Si noti che, per la normalizzazione del batch e dell’istanza, la media e la std sono fissate dopo l’addestramento, anziché computate nuovamente quando la rete è usata per l’inferenza, perché, al fine di applicare la normalizzazione, sono necessari più istanze di addestramento. Ciò non è necessario per la normalizzazione di gruppo e dello strato, in quanto la loro normalizzazione viene effettuata sulla singola istanza di addestramento.

La morte dell’ottimizzazione

Qualche volta possiamo avventurarci in campi di cui non conosciamo nulla e migliorare come lì si implementano le cose. Uno di questi esempi è l’utilizzo di reti neurali profonde nel campo dell’imaging a risonanza magnetica (MRI) per accelerare la ricostruzione delle immagini ottenute tramite MRI.

Fig. 5: A volte funziona!

Ricostruzione da MRI

Nel problema tradizionale della ricostruzione da MRI, i dati grezzi sono ottenuti da un macchinario per l’MRI e le immagini sono ricostruite utilizzando un semplice sequenza d’istruzioni (algoritmo). Il macchinario cattura i dati in uno spazio bidimensionale di Fourier, una riga o una colonna alla volta (ogni pochi millisecondi). Questo input grezzo è composto da un canale della frequenza e un canale della fase e il valore rappresenta l’ampiezza di una sinusoide con quella frequenza e quella fase specifica. Detto in maniera semplice, può essere vista come un’immagine a valori complessi, con un canale reale e un canale immaginario. Se applichiamo la trasformata di Fourier inversa a questo input, ovvero, sommiamo tutte queste sinusoidi pesate per il loro rispettivo valore, otteniamo l’immagine anatomica di partenza.

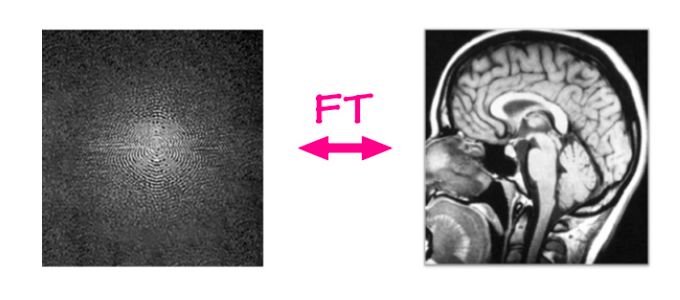
Fig. 6: ricostruzione da MRI

Al momento, esiste una mappatura lineare dal dominio di Fourier al dominio dell’immagine e questa mappatura è molto efficiente, c’impiega pochissimi millisecondi, indipendentemente dalla grandezza dell’immagine. Ma la domanda è, si può essere ancora più veloci?

MRI accelerato

Il nuovo problema che dev’essere risolto è l’MRI accelerato, dove per accelerazione intendiamo che si deve svolgere il processo di ricostruzione dell’MRI ancora più veloce. Vogliamo far funzionare i macchinari più velocemente, riuscendo contemporaneamente a produrre immagini della stessa qualità. Un modo per fare ciò, e anche quello di più successo, è non catturare tutte le colonne della scansione MRI. Possiamo saltare alcune colonne in maniera casuale, anche se, in pratica, è utile catturare le colonne centrali, in quanto convogliano una buona parte dell’informazione di tutta l’immagine, ma al di fuori di esse, catturiamo le colonne casualmente. Il problema è che non possiamo più utilizzare la mappatura lineare per ricostruire l’immagine. L’immagine più a destra della Fig. 7 mostra l’output della mappatura lineare applicata ad un sotto-campionamento dello spazio di Fourier. È chiaro che questo metodo non ci fornisce un output utile, e che c’è del margine per fare qualcosa di un po’ più intelligente.

Figure 7: Mappatura lineare di un sotto-campionamento nello spazio di Fourier

Compressed sensing

Una delle più grandi svolte di tanti anni di matematica teorica è stata la tecnica del compressed sensing. Una pubblicazione di Candes et al. mostra che, teoricamente, si dovrebbe essere in grado di ottenere una ricostruzione perfetta dal sotto-campionamento nello spazio di Fourier. In altre parole, quando il segnale che stiamo cercando di ricostruire è sparso o strutturato in maniera sparsa, allora è possibile ricostruirlo perfettamente a partire da un numero di campionamenti minore. Ma ci sono dei requisiti pratici affinché ciò funzioni – non si deve campionare in maniera casuale, piuttosto dobbiamo farlo in maniera incoerente – anche se in pratica, si finisce per campionare casualmente. Inoltre, è equivalente in termini di tempo campionare una colonna intera o solo metà, così in pratica si campiona sempre un’intera colonna.

Un’altra condizione che si deve verificare è la sparsità nell’immagine, dove per sparsità s’intende che ci sono molti zeri (o pixel neri) nell’immagine. L’input grezzo può essere rappresentato in maniera sparsa se operiamo una decomposizione in lunghezze d’onda, ma questa decomposizione ci fornisce un’immagine approssimativamente sparsa, non perfettamente sparsa. Perciò, questo approccio ci dà una ricostruzione buona ma non perfetta, come possiamo notare in Fig. 8. Ad ogni modo, se l’input fosse sparso nel dominio delle lunghezze d’onda, sicuramente otterremmo un’immagine perfetta.

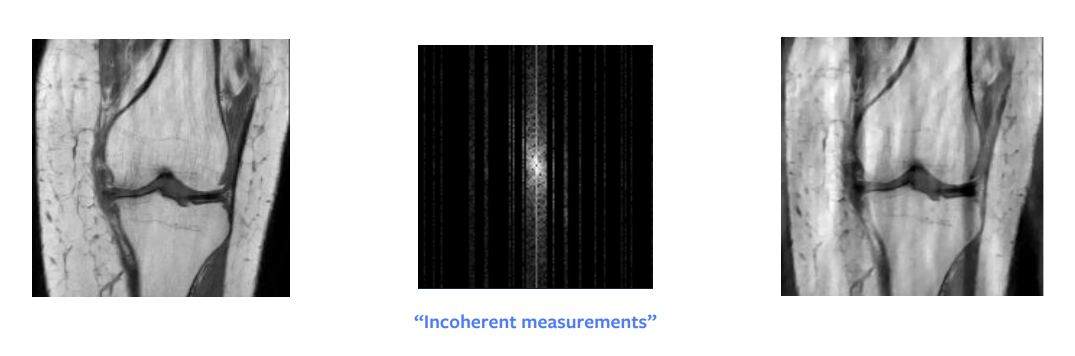
Fig. 8: *Compressed sensing*

Il compressed sensing si basa sulla teoria dell’ottimizzazione. Possiamo ottenere questa ricostruzione risolvendo un piccolo problema di ottimizzazione il quale presenta un ulteriore termine di regolarizzazione:

dove $M$ è la funzione di mascheramento che azzera gli elementi non campionati, $\mathcal{F}$ è la trasformata di Fourier, $y$ sono i dati osservati nel dominio di Fourier, $\lambda$ è la forza del coefficiente di penalizzazione corrispondente alla regolarizzazione e $V$ è la funzione di regolarizzazione.

Il problema di ottimizzazione dev’essere risolto per ogni istante di tempo, o ogni “fetta” di una scansione MRI, il che spesso prende ben più tempo della scansione stessa. Ciò ci dà un’altra ragione per cercare qualcosa di meglio.

Chi ha bisogno dell’ottimizzazione?

Anziché risolvere un piccolo problema di ottimizzazione ad ogni istante temporale, perché non usare una grande rete neurale per produrre direttamente la soluzione richiesta? La nostra speranza è che possiamo addestrare una rete neurale con sufficiente complessità in modo tale da risolvere il problema di ottimizzazione in un passo e da produrre un output che sia tanto buono quanto quello ottenuto risolvendo il problema di ottimizzazione per ogni passo temporale.

dove $B$ è il nostro modello di apprendimento profondo e $y$ sono i dati osservati nel dominio di Fourier.

15 anni fa, questo approccio era difficile – ma oggidì è di più facile implementazione. La Fig. 9 mostra il risultato di un approccio a questo problema utilizzando l’apprendimento profondo; possiamo vedere come l’output sia molto migliore di quello ottenuto tramite l’approccio di compressed sensing, e risulti anche più simile alla scansione completa.

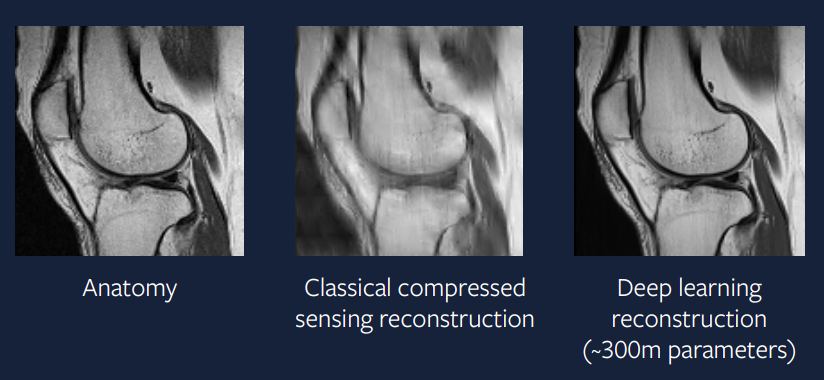
Figure 9: approccio tramite apprendimento profondo

Il modello utilizzato per generare questa ricostruzione utilizza l’ottimizzatore ADAM, strati di normalizzazione di gruppo e una rete neurale convoluzionale basata su U-Net. Un approccio di questo genere è molto vicino alle applicazioni pratiche e, sperabilmente, vedremo queste scansioni MRI accelerate utilizzate nella prassi clinica entro pochi anni. –>