Tecniche di ottimizzazione I

Discesa del gradiente

Iniziamo il nostro studio delle tecniche di ottimizzazione con il più basilare e peggiore (motivazioni a seguire) metodo fra quelli che vedremo, la discesa del gradiente.

Problema:

Soluzione iterativa:

dove:

• $w_{k+1}$ è il valore aggiornato dopo la $k$-esima iterazione,
• $w_k$ è il valore iniziale prima della $k$-esima iterazione,
• $\gamma_k$ è la dimensione del passo,
• $\nabla f(w_k)$ è il gradiente di $f$.

L’assunzione che facciamo è che la funzione $f$ sia continua e differenziabile. Il nostro scopo è trovare il punto più basso (“valle”) della funzione da ottimizzare. In ogni caso, la direzione corrente di questa valle è sconosciuta. Possiamo solamente orientarci a livello locale, quindi la direzione del gradiente negativo è la miglior informazione che possediamo. Fare un piccolo passo in questa direzione può solo che avvicinarci al minimo. Una volta che abbiamo preso effettuato questo passo, possiamo nuovamente computare il nuovo gradiente e nuovamente muoverci di una breve distanza in quella direzione, fintantoché non raggiungiamo la valle. Quindi, essenzialmente, tutto ciò che fa la discesa del gradiente è seguire la direzione in cui il pendio è maggiore (gradiente negativo).

Il parametro $\gamma$ nell’equazione di aggiornamento iterativo è chiamato dimensione del passo. Generalmente, non ne conosciamo il valore ottimale; dobbiamo dunque provare con diversi valori. La prassi è provare una serie di valori in scala logaritmica e usare il migliore fra questi. Ci sono differenti scenari che possono verificarsi. L’immagine sopra descrive questi scenari per una quadratica monodimensionale. Se il livello di apprendimento è troppo basso, allora facciamo una progressione lenta verso il minimo. In ogni caso, questo potrebbe impiegare più tempo di quanto a disposizione. È generalmente molto difficile (o impossibile) ottenere una dimensione del passo che ci porti direttamente al minimo. Ciò che vorremmo idealmente è avere una dimensione del passo un minimo più grande rispetto a quella ottimale. In pratica, ciò fornisce la convergenza più rapida. Comunque, se usiamo un livello di apprendimento troppo grande, le iterazioni si allontanano progressivamente dal minimo ed otteniamo una divergenza. In pratica, vorremmo usare un livello di apprendimento che sia un minimo meno di quello che porti alla divergenza.

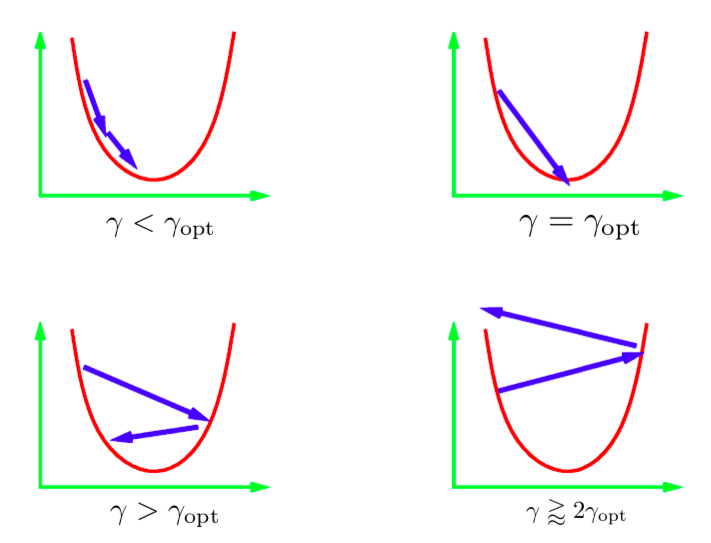
Figure 1: dimensione del passo per una quadratica monodimensionale

Discesa stocastica del gradiente

Nella discesa stocastica del gradiente, sostituiamo il vettore del gradiente corrente con una stima stocastica di quest’ultimo. Specificamente, per una rete neurale, la stima stocastica è ottenuta dal gradiente della funzione di perdita per un singolo punto (istanza) dei dati.

Sia $f_i$ la perdita della rete per l’istanza $i$-esima.

La funzione da minimizzare è $f$, la perdita totale su tutte le istanze.

In SGD, aggiorniamo i pesi in base al gradiente di $f_i$ (anziché alla perdita totale $f$).

Se $i$ è scelto casualmente, allora $f_i$ è uno stimatore di $f$ rumoroso ma non distorto, e può essere scritto matematicamente come:

Come risultato di ciò, il passo $k$-esimo di SGD è in media identico al passo $k$-esimo della discesa del gradiente operata su tutte le istanze:

Quindi, ogni aggiornamento di SGD è lo stesso, in media, di un aggiornamento calcolato su tutti i dati. Comunque, SGD non è solo un SGD rapido con rumore. Oltre a essere più rapido, SGD ci può anche fornire risultati migliori di una discesa del gradiente completa. Il rumore di SGD ci può anche aiutare ad evitare i minimi locali poco profondi e aiutarci a trovare un migliore (più profondo) punto di minimo. Questo fenomeno è chiamato annealing (“ricottura”).

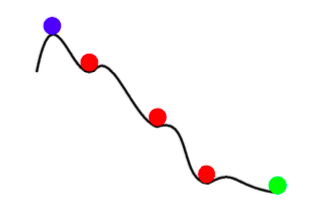
Figure 2: *Annealing* con SGD

Riassumendo, i vantaggi della discesa stocastica del gradiente sono i seguenti:

1. C’è molta informazione ridondante fra le varie istanze. SGD ne previene in buona parte la computazione.
2. Per le prime iterazioni, il rumore è piccolo se comparato all’informazione trasmessa dal gradiente. Quindi un passo del SGD è virtualmente tanto buono quanto un passo del GD.
3. Annealing – il rumore nell’aggiornamento del SGD può prevenire la convergenza verso minimi locali cattivi (poco profondi).
4. La discesa stocastica del gradiente e drasticamente più economica da un punto di vista computazionale (in quanto il gradiente non dev’essere ricalcolato su tutte le istanze).

Mini-batching

La tecnica chiamata mini-batching prevede che si calcoli la funzione di perdita su più istanze selezionate anziché su una sola istanza. Questo riduce il rumore nel passo di aggiornamento.

Spesso siamo in grado di fare un miglior uso del nostro hardware utilizzando mini batch invece di una singola istanza. Per esempio, le GPU sono sottoutilizzate quando usiamo singole istanze per l’addestramento. Le tecniche distribuite di addestramento di reti suddividono un grosso mini-batch fra più macchine di un cluster e ne aggregano i gradienti risultanti. Facebook ha recentemente addestrato una rete sul dataset ImageNet in un’ora usando l’addestramento distribuito.

È importante notare che la discesa del gradiente non dovrebbe mai essere utilizzata con batch grandi quanto il dataset. Nel caso in cui si voglia addestrare una rete in questo modo, si usi la tecnica di ottimizzazione nota come LBFGS. PyTorch e SciPy implementano tutte e due questa tecnica.

Momento

Al momento, abbiamo due quantità da aggiornare iterativamente, anziché una sola. Le formule di aggiornamento sono le seguenti:

$p$ è chiamato momento del SGD. A ogni passo di aggiornamento, aggiungiamo al gradiente stocastico il vecchio valore del momento, dopo averlo “smorzato” di un fattore $\beta$ (il cui valore è compreso fra 0 e 1). $p$ può essere pensato come una media a valori mobili del gradiente. Infine muoviamo $w$ nella direzione del nuovo momento $p$.

Forma alternativa: metodo stocastico della palla pesante

Questa forma è matematicamente equivalente alla precedente. Qui, il passo successivo è una combinazione della direzione della direzione del passo precedente ($w_k - w_{k-1}$) e il nuovo gradiente negativo.

Intuizione

Il momento del SGD è simile al concetto fisico del momento. Il processo di ottimizzazione può essere assimilato a quello del rotolamento di una palla pesante giù per una collina. Il momento mantiene la palla in movimento nella stessa direzione nella quale si sta muovendo. Il gradiente può essere pensato come una forza che spinge la palla in un’altra direzione.

Fig. 3: effetto del momento
Fonte: distill.pub

Anziché apportare grossi cambiamenti nella direzione di moto (come nella figura a sinistra), il momento ne causa di modesti. Il momento smorza le oscillazioni che sono molto comuni quando usiamo solo SGD.

Il parametro $\beta$ è chiamato “fattore di smorzamento”. $\beta$ dev’essere più grande di zero, perché se fosse uguale a zero, si starebbe facendo una semplice discesa del gradiente. Deve altresì essere più piccolo di 1, altrimenti il tutto esploderebbe. Valori piccoli di $\beta$ corrispondono a più repentini cambi di direzione. Per valori più grandi, è richiesto un maggior tempo per “curvare”.

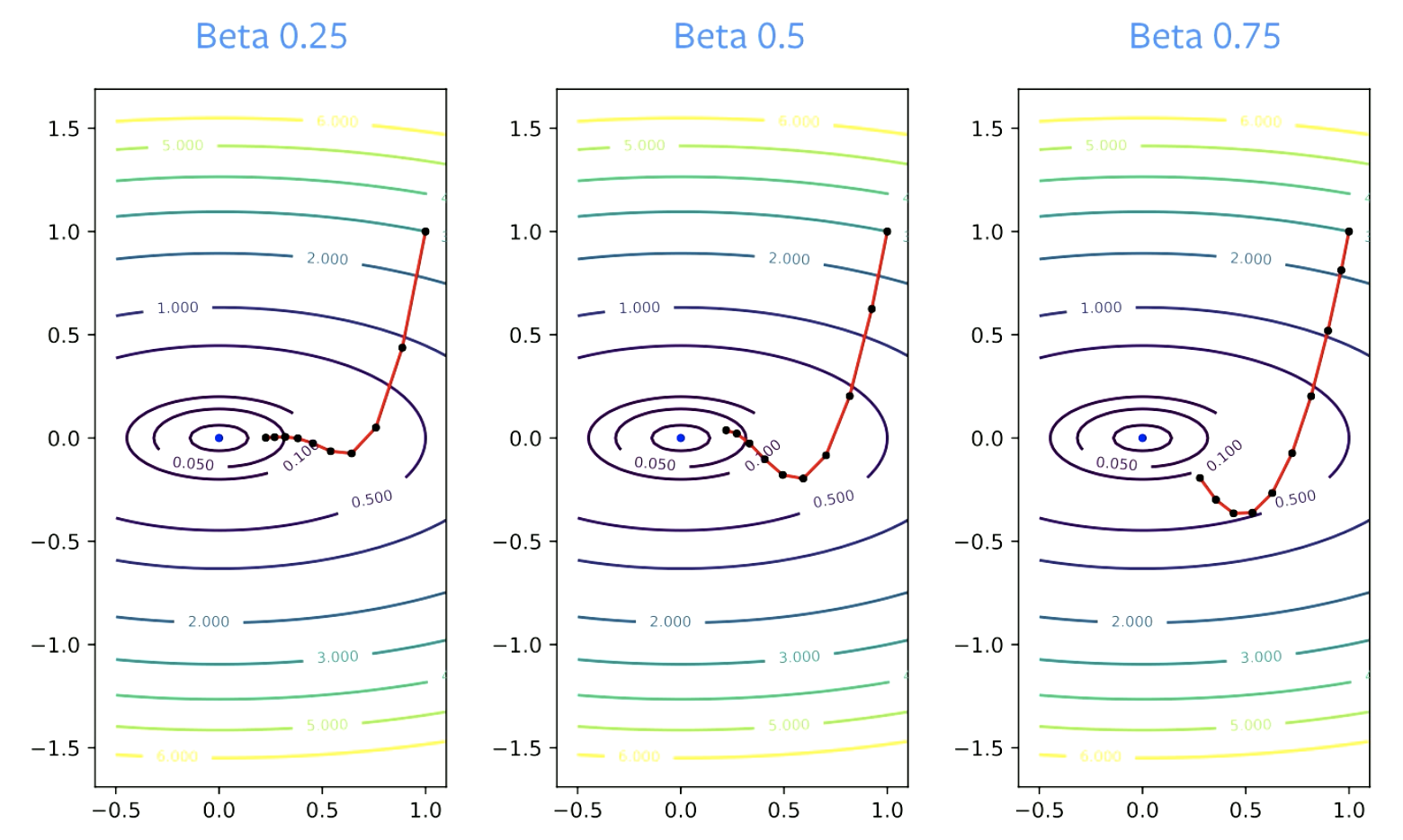
Figure 4: effetto di $\beta$ sulla convergenza

Linee guida pratiche

Il momento dev’essere praticamente sempre utilizzato con la discesa stocastica del gradiente. Valori di $\beta$ pari a 0.9 o 0.99 quasi sempre danno buoni risultati.

Il parametro della lunghezza del passo, usualmente, dev’essere decrementato quando il parametro del momento aumenta per mantenere la convergenza. Se $\beta$ cambia da 0.9 a 0.99, il livello di apprendimento dev’essere decrementato di un fattore di 10.

Perché il momento funziona’?

Accelerazione

Di seguito sono presentate le regole di aggiornamento per il momento di Nesterov:

Col momento di Nesterov, si può ottenere una convergenza accelerata se si scelgono attentamente le costanti. Ma ciò si applica solo a problemi convessi e non a reti neurali.

Molti sostengono che il momento classico sia anch’esso un metodo accelerato, ma, in realtà, è accelerato solo per quadratiche. Inoltre, l’accelerazione non funziona bene con SGD, in quanto quest’ultimo ha rumore e l’accelerazione non sinergizza bene col rumore. Di conseguenza nonostante vi sia un po’ di accelerazione anche nel SGD con momento, esso non è da solo una buona spiegazione delle buone performance della tecnica.

Lisciamento del rumore

Probabilmente, una motivazione più pratica del perché il momento funzioni è il lisciamento del rumore.

Il momento fa una media dei gradienti. È una media mobile dei gradienti che utilizziamo per ogni passo di aggiornamento.

Teoricamente, affinché SGD funzioni, dovremmo prendere una media su tutti i passi di aggiornamento:

Il bello del SGD con momento è che questa media non è più necessaria. Il momento dona un lisciamento al processo di ottimizzazione, il che rende ogni aggiornamento una buona approssimazione verso la soluzione. Con SGD si vuole fare una media di un certo numero di aggiornamenti e poi fare un passo in tale direzione.

Sia l’accelerazione che il lisciamento del rumore contribuiscono alle alte performance del momento.

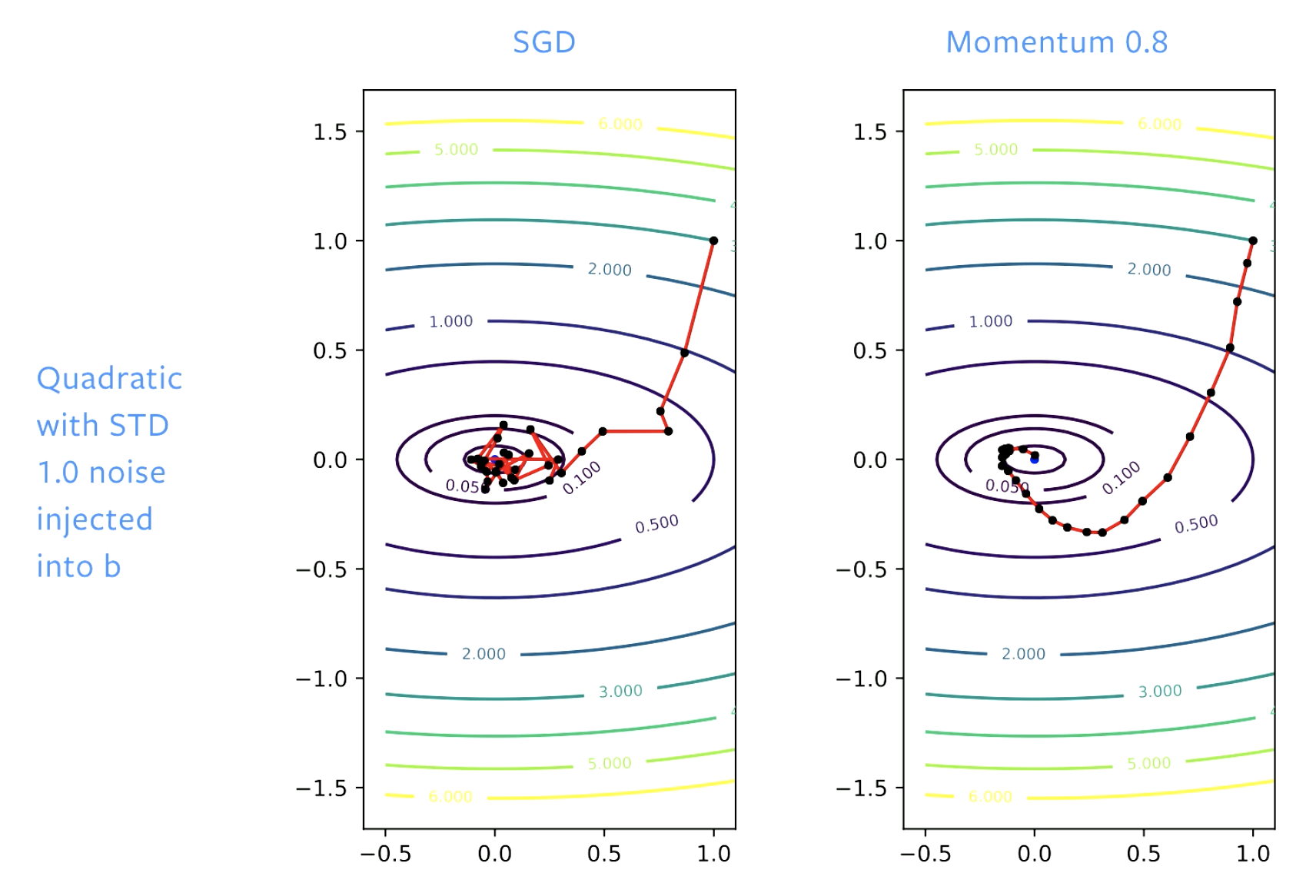
Figure 5: SGD vs. momento

Con SGD, facciamo in prima battuta buoni progressi verso la soluzione, ma quando raggiungiamo una conca (il fondo della valle) continuiamo a rimbalzare attorno al fondale. Se aggiustiamo il livello di apprendimento, continueremo a rimbalzare, anche se un po’ più lentamente. Col momento, andiamo ad “addolcire” i passi, così che non c’è più questo effetto di “rimbalzi”.