Algebra lineare e convoluzioni

🎙️ Alfredo Canziani

Ripasso di algebra lineare

Questo capitolo è un ripasso di algebra lineare base nel contesto delle reti neurali. Iniziamo con un semplice strato nascosto $\boldsymbol{h}$:

\[\boldsymbol{h} = f(\boldsymbol{z})\]

L’output è una funzione nonlineare $f$ applicata a un vettore $z$. Qui $z$ è l’output di una trasformazione affine $\boldsymbol{A} \in\mathbb{R^{m\times n}}$ applicata al vettore di input $\boldsymbol{x} \in\mathbb{R^n}$:

\[\boldsymbol{z} = \boldsymbol{A} \boldsymbol{x}\]

Per semplicità, i bias sono omessi. L’equazione lineare può essere espansa come:

\[\boldsymbol{A}\boldsymbol{x} = \begin{pmatrix} a_{11} & a_{12} & \cdots & a_{1n}\\ a_{21} & a_{22} & \cdots & a_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{m1} & a_{m2} & \cdots & a_{mn} \end{pmatrix} \begin{pmatrix} x_1 \\ \vdots \\x_n \end{pmatrix} = \begin{pmatrix} \text{---} \; \boldsymbol{a}^{(1)} \; \text{---} \\ \text{---} \; \boldsymbol{a}^{(2)} \; \text{---} \\ \vdots \\ \text{---} \; \boldsymbol{a}^{(m)} \; \text{---} \\ \end{pmatrix} \begin{matrix} \rvert \\ \boldsymbol{x} \\ \rvert \end{matrix} = \begin{pmatrix} {\boldsymbol{a}}^{(1)} \boldsymbol{x} \\ {\boldsymbol{a}}^{(2)} \boldsymbol{x} \\ \vdots \\ {\boldsymbol{a}}^{(m)} \boldsymbol{x} \end{pmatrix}_{m \times 1}\]

dove $\boldsymbol{a}^{(i)}$ è la $i$-esima riga della matrice $\boldsymbol{A}$.

Per comprendere il significato di questa trasformazione, analizziamo una componente di $\boldsymbol{z}$ come $a^{(1)}\boldsymbol{x}$. Sia $n=2$, quindi $\boldsymbol{a} = (a_1,a_2)$ e $\boldsymbol{x} = (x_1,x_2)$.

$\boldsymbol{a}$ e $\boldsymbol{x}$ possono essere visualizzati come vettori nel piano cartesiano. Ora, se l’angolo tra $\boldsymbol{a}$ e $\hat{\boldsymbol{\imath}}$ è $\alpha$ è l’angolo fra $\boldsymbol{x}$ e $\hat{\boldsymbol{\imath}}$ è $\xi$, allora le formule trigonometriche $a^\top\boldsymbol{x}$ possono essere espanse come:

\[\begin {aligned} \boldsymbol{a}^\top\boldsymbol{x} &= a_1x_1+a_2x_2\\ &=\lVert \boldsymbol{a} \rVert \cos(\alpha)\lVert \boldsymbol{x} \rVert \cos(\xi) + \lVert \boldsymbol{a} \rVert \sin(\alpha)\lVert \boldsymbol{x} \rVert \sin(\xi)\\ &=\lVert \boldsymbol{a} \rVert \lVert \boldsymbol{x} \rVert \big(\cos(\alpha)\cos(\xi)+\sin(\alpha)\sin(\xi)\big)\\ &=\lVert \boldsymbol{a} \rVert \lVert \boldsymbol{x} \rVert \cos(\xi-\alpha) \end {aligned}\]

L’output misura l’allineamento dell’input ad una specifica riga della matrice $\boldsymbol{A}$. Ciò può essere compreso dall’osservazione dell’angolo fra due vettori, $\xi-\alpha$. Quando $\xi = \alpha$, i due vettori sono perfettamente allineati ed il massimo è raggiunto. If $\xi - \alpha = \pi$, allora $\boldsymbol{a}^\top\boldsymbol{x}$ raggiunge il suo minimo e i due vettori sono orientati in versi opposti. Riassumendo, la trasformazione lineare permette di visualizzare la proiezione di un input in vari orientamenti, come definito da $A$. Questa intuizione è pure espandibile in un numero maggiore di dimensioni.

Un altro modo di capire la trasformazione lineare passa per la comprensione che $\boldsymbol{z}$ può anche essere espanso come:

\[\boldsymbol{A}\boldsymbol{x} = \begin{pmatrix} \vert & \vert & & \vert \\ \boldsymbol{a}_1 & \boldsymbol{a}_2 & \cdots & \boldsymbol{a}_n \\ \vert & \vert & & \vert \\ \end{pmatrix} \begin{matrix} \rvert \\ \boldsymbol{x} \\ \rvert \end{matrix} = x_1 \begin{matrix} \rvert \\ \boldsymbol{a}_1 \\ \rvert \end{matrix} + x_2 \begin{matrix} \rvert \\ \boldsymbol{a}_2 \\ \rvert \end{matrix} + \cdots + x_n \begin{matrix} \rvert \\ \boldsymbol{a}_n \\ \rvert \end{matrix}\]

L’output è una somma pesata di colonne della matrice $\boldsymbol{A}$. Di conseguenza, il segnale non è null’altro che una composizione dell’input.

Estensione dell’algebra lineare alle convoluzioni

Ora, estendiamo l’algebra lineare alle convoluzioni utilizzando come esempio l’analisi di dati audio. Iniziamo rappresentando uno strato densamente connesso come una forma di moltiplicazione matriciale:

\[\begin{bmatrix} w_{11} & w_{12} & w_{13}\\ w_{21} & w_{22} & w_{23}\\ w_{31} & w_{32} & w_{33}\\ w_{41} & w_{42} & w_{43} \end{bmatrix} \begin{bmatrix} x_1\\ x_2\\ x_3 \end{bmatrix} = \begin{bmatrix} y_1\\ y_2\\ y_3\\ y_4 \end{bmatrix}\]

In questo esempio, la matrice dei pesi ha una dimensione di $4 \times 3$, il vettore di input ha una dimensione di $3 \times 1$ e il vettore di output ha una dimensione di $4 \times 1$.

Comunque, i dati audio sono molto più lunghi (ben più di 3 campionamenti). Il numero di campionamenti dei dati audio è uguale alla durata dell’audio (es. 3 secondi) moltiplicato per il rapporto di campionamento (es. 22.05 kHz). Come mostrato sotto, il vettore di input $\boldsymbol{x}$ sarà piuttosto lungo. In maniera analoga, la matrice dei pesi diventerà piuttosto “grossa”.

\[\begin{bmatrix} w_{11} & w_{12} & w_{13} & w_{14} & \cdots &w_{1k}& \cdots &w_{1n}\\ w_{21} & w_{22} & w_{23}& w_{24} & \cdots & w_{2k}&\cdots &w_{2n}\\ w_{31} & w_{32} & w_{33}& w_{34} & \cdots & w_{3k}&\cdots &w_{3n}\\ w_{41} & w_{42} & w_{43}& w_{44} & \cdots & w_{4k}&\cdots &w_{4n} \end{bmatrix} \begin{bmatrix} x_1\\ x_2\\ x_3\\ x_4\\ \vdots\\ x_k\\ \vdots\\ x_n \end{bmatrix} = \begin{bmatrix} y_1\\ y_2\\ y_3\\ y_4 \end{bmatrix}\]

La formulazione qui sopra sarà difficile da addestrare. Fortunatamente vi sono metodi per semplificarla.

Proprietà: localizzazione

A causa della localizzazione (ovvero, non siamo interessati a punti lontani) dei dati, $w_{1k}$ della matrice sopra può essere riempito di zeri quando $k$ è relativamente grande. Di conseguenza, la prima riga della matrice diviene un nucleo di dimensione 3. Denotiamo questo nucleo come $\boldsymbol{a}^{(1)} = \begin{bmatrix} a_1^{(1)} & a_2^{(1)} & a_3^{(1)} \end{bmatrix}$.

\[\begin{bmatrix} a_1^{(1)} & a_2^{(1)} & a_3^{(1)} & 0 & \cdots &0& \cdots &0\\ w_{21} & w_{22} & w_{23}& w_{24} & \cdots & w_{2k}&\cdots &w_{2n}\\ w_{31} & w_{32} & w_{33}& w_{34} & \cdots & w_{3k}&\cdots &w_{3n}\\ w_{41} & w_{42} & w_{43}& w_{44} & \cdots & w_{4k}&\cdots &w_{4n} \end{bmatrix} \begin{bmatrix} x_1\\ x_2\\ x_3\\ x_4\\ \vdots\\ x_k\\ \vdots\\ x_n \end{bmatrix} = \begin{bmatrix} y_1\\ y_2\\ y_3\\ y_4 \end{bmatrix}\]

Proprietà: stazionarietà

I segnali di dati naturali hanno la proprietà di stazionarietà (ovvero, certi motivi si ripeteranno). Ciò ci aiuta a riutilizzare il nucleo $\mathbf{a}^{(1)}$ che abbiamo definito precedentemente. Usiamo questo nucleo posizionandolo avanti di una posizione per ogni istante (ovvero, il passo è 1), ottenendo quanto segue:

\[\begin{bmatrix} a_1^{(1)} & a_2^{(1)} & a_3^{(1)} & 0 & 0 & 0 & 0&\cdots &0\\ 0 & a_1^{(1)} & a_2^{(1)} & a_3^{(1)} & 0&0&0&\cdots &0\\ 0 & 0 & a_1^{(1)} & a_2^{(1)} & a_3^{(1)} & 0&0&\cdots &0\\ 0 & 0 & 0& a_1^{(1)} & a_2^{(1)} &a_3^{(1)} &0&\cdots &0\\ 0 & 0 & 0& 0 & a_1^{(1)} &a_2^{(1)} &a_3^{(1)} &\cdots &0\\ \vdots&&\vdots&&\vdots&&\vdots&&\vdots \end{bmatrix} \begin{bmatrix} x_1\\ x_2\\ x_3\\ x_4\\ \vdots\\ x_k\\ \vdots\\ x_n \end{bmatrix}\]

Sia la parte in alto a destra che quella in basso a sinistra della matrice sono riempite con zeri grazie alla localizzazione, dando origine a sparsità. L’utilizzo continuo di un certo nucleo viene denominato condivisione dei pesi.

Strati multipli composti da matrici di Toeplitz

Dopo questi cambiamenti, rimaniamo con un numero di parametri pari a 3 ($a_1,a_2,a_3$). Rispetto alla precedente matrice dei pesi, che era composta da 12 parametri ($w_{11},w_{12},\cdots,w_{43}$), il numero attuale di parametri è troppo restrittivo e vorremmo espanderlo.

La precedente matrice può essere considerata come uno strato (ovvero, uno strato convoluzionale) con nucleo $\boldsymbol{a}^{(1)}$. Quindi, possiamo costruire più strati con i nuclei $\boldsymbol{a}^{(2)}$, $\boldsymbol{a}^{(3)}$, ecc., aumentando dunque i parametri.

Ogni strato è composto da una matrice contenente solo un nucleo che viene replicato più volte. Questo tipo di matrice si chiama matrice di Toeplitz. In ogni matrice di questo tipo, ogni diagonale discendente da sinistra verso destra è costante. Le matrici di Toeplitz qui utilizzate sono, inoltre, matrici sparse.

Dato il primo nucleo $\boldsymbol{a}^{(1)}$ e il vettore di input $\boldsymbol{x}$, la prima componente dell’output dato questo strato è $a_1^{(1)} x_1 + a_2^{(1)} x_2 + a_3^{(1)}x_3$. Dunque, il vettore di output completo assume una forma del tipo:

\[\begin{bmatrix} \mathbf{a}^{(1)}x[1:3]\\ \mathbf{a}^{(1)}x[2:4]\\ \mathbf{a}^{(1)}x[3:5]\\ \vdots \end{bmatrix}\]

Lo stesso procedimento basato sul prodotto matriciale può essere applicato negli strati convoluzionali successivi con altri nuclei (come $\boldsymbol{a}^{(2)}$ e $\boldsymbol{a}^{(3)}$) ottenendo risultati simili.

Ascoltare le convoluzioni - Jupyter Notebook

In questo notebook, esploriamo la convoluzione come un “prodotto scalare mobile”.

La libreria librosa ci permette di caricare il file audio $\boldsymbol{x}$ e il suo rapporto di campionamento. In questo caso, ci sono 70641 campioni, il rapporto è 22.05kHz e la lunghezza totale della traccia è 3.2s. Il segnale audio importato è ondulato (fare riferimento alla Fig. 1) e possiamo ipotizzarne il suono dall’ampiezza riportata nell’asse $y$. Il segnale audio $x(t)$ è il suono riprodotto quando chiudiamo Windows (fare rifermento alla Fig. 2).

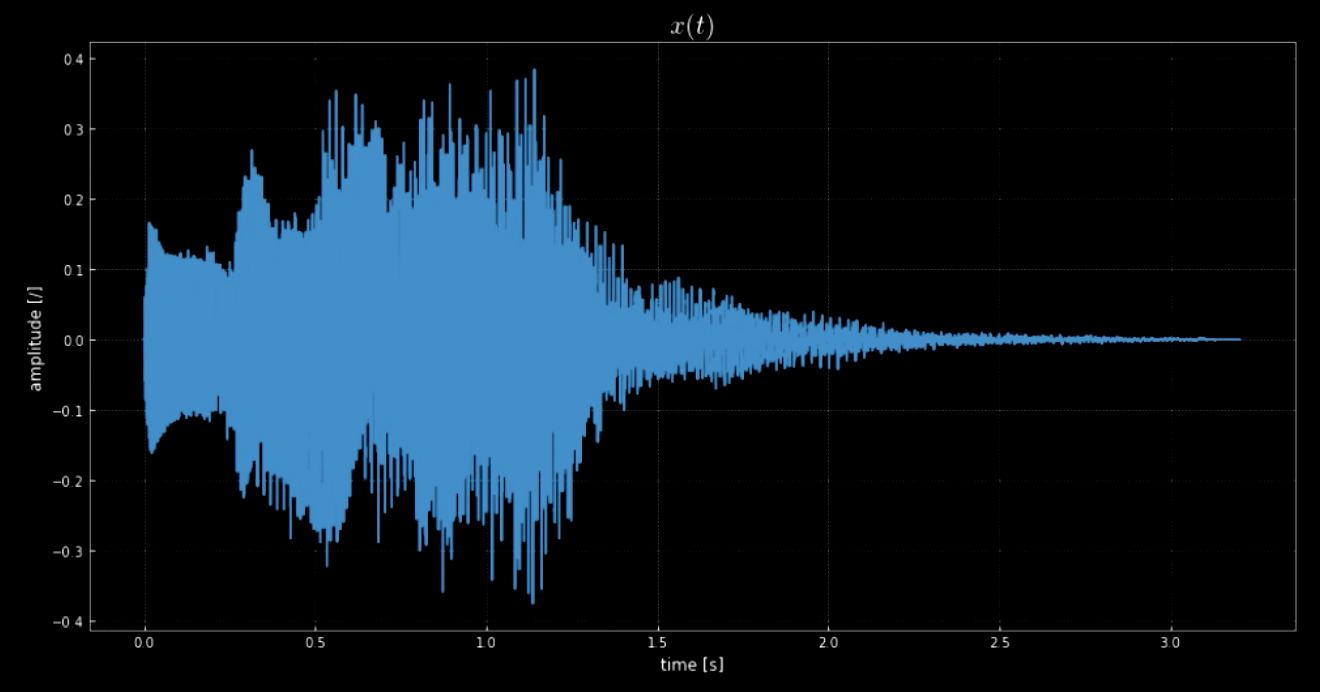
Fig. 1: Una visualizzazione del segnale audio.

Fig. 2: Note del segnale audio di cui sopra.

Dobbiamo separare le note dalla forma delle onde. Per fare ciò, se utilizzassimo la trasformata di Fourier (FT), tutte le note sarebbero estratte contemporaneamente e sarebbe complicato risalire alla localizzazione e al tempo di ogni tono. Quindi, necessitiamo una FT localizzata (anche conosciuta come spettrogramma). Come si osserva dallo spettrogramma (fare riferimento alla Fig. 3), toni diversi raggiungono un picco a frequenze diverse (ad es., il primo tono ha un massimo a 1600). Concatenando i quattro toni alle loro frequenze, otteniamo una versione “a toni” del segnale originario.

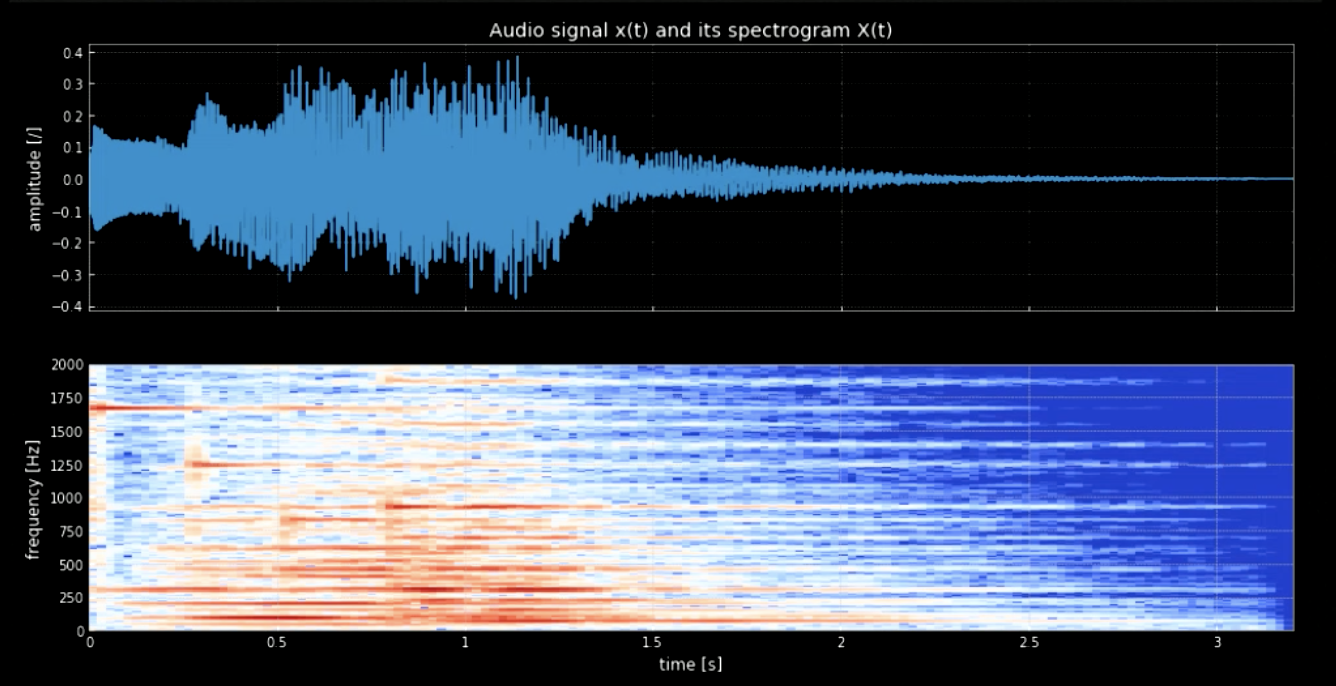
Fig. 3: Il segnale audio e il suo spettrogramma.

La convoluzione del segnale di input con tutti i toni (tutte le note di un pianoforte, per esempio) ci può aiutare ad estrarre tutte le note del pezzo di input (ovvero, gli istanti in cui l’audio si abbina al nucleo specifico). Gli spettrogrammi del segnale originario del segnale dei toni concatenati è mostrato in Fig. 4, mentre le frequenze del segnale originario e dei quattro toni sono mostrate in Fig. 5. Il grafico della convoluzione dei quattro nuclei col segnale di input (segnale originario) è mostrato in Fig. 6. Quest’ultima figura e le tracce audio della convoluzione provano l’efficacia della convoluzione ai fini dell’estrazione delle note.

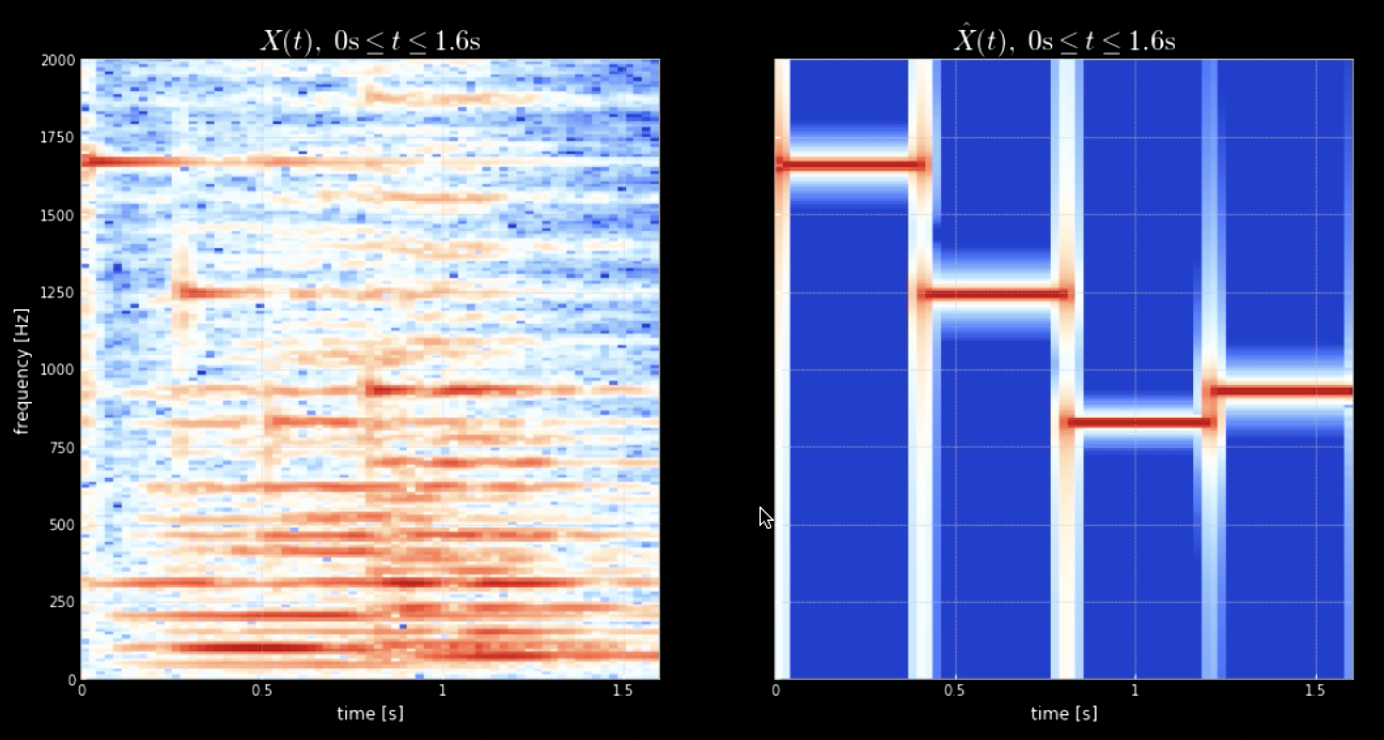
Fig. 4: Spettrogramma del segnale originario (sinistra) e spettrogramma della concatenazione dei toni (destra).

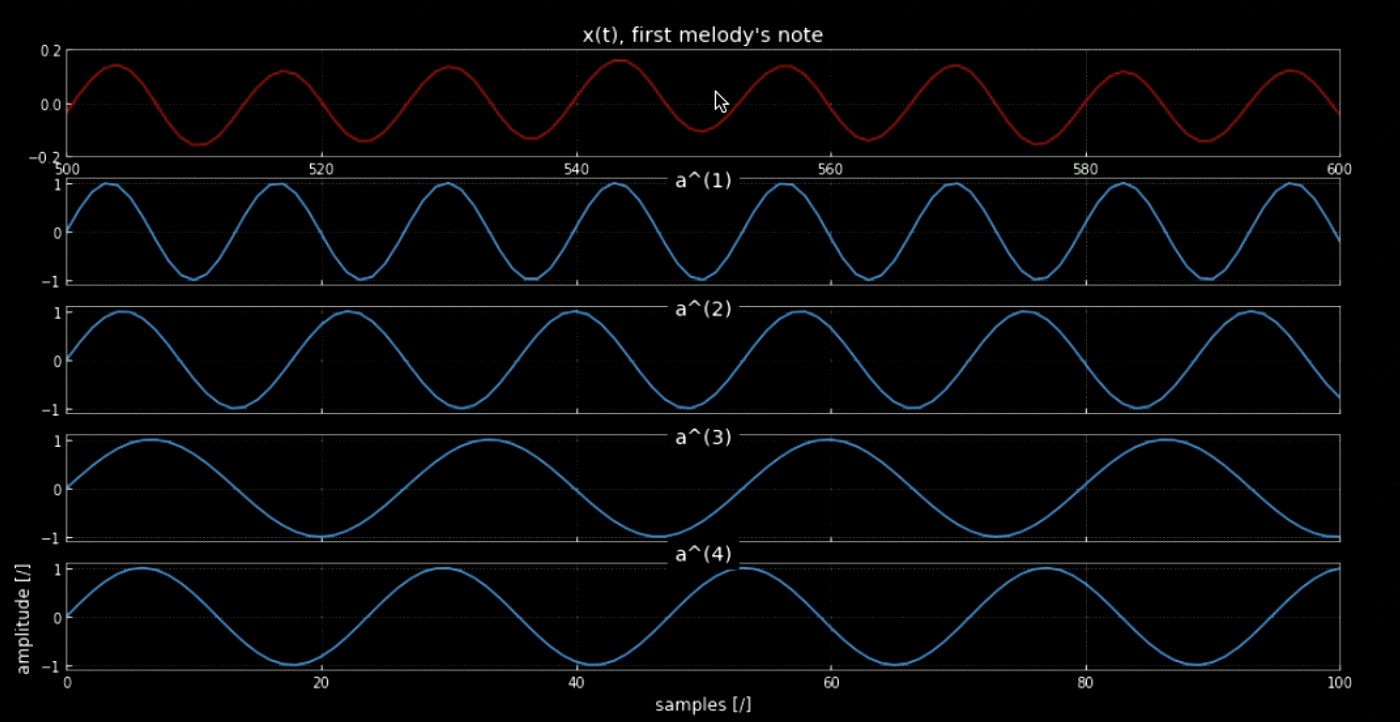
Fig. 5: La nota della prima melodia .

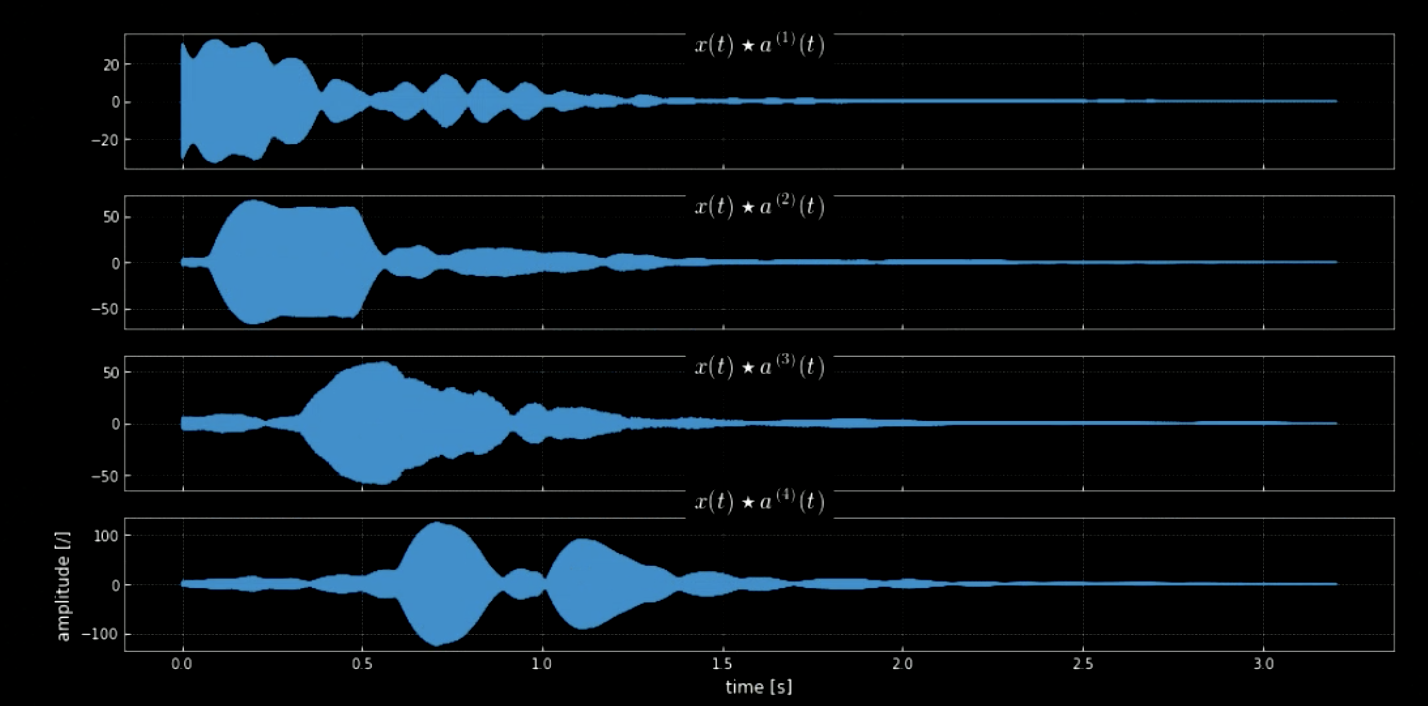
Fig. 6: La convoluzione dei quattro nuclei.

Dimensionalità di diversi dataset

L’ultima parte è una digressione rapida sulle differenti rappresentazioni della dimensionalità ed esempi collegati. Qui consideriamo che l’insieme di input $X$ sia composto da funzioni che mappano il dominio $\Omega$ ai canali $c$.

Esempi

• Dati audio: il dominio è 1-D, il segnale è discreto e indicizzato dal tempo; il numero di canali $c$ può variare fra 1 (mono), 2 (stereo), 5+1 (Dolby 5.1), ecc.
• Immagini: il dominio è 2-D (pixel); $c$ può variare fra 1 (scala di grigi), 3 (colori), 20 (iperspettrale), ecc.
• Relatività ristretta: il dominio è $\mathbb{R^4} \times \mathbb{R^4}$ (spazio-tempo $\times$ quadrimpulso); quando $c = 1$, è chiamato hamiltoniano.

Fig. 7: Differenti dimensioni di svariati tipi di segnale.

---

📝 Yuchi Ge, Anshan He, Shuting Gu, and Weiyang Wen
marcozullich
18 Feb 2020