Proprietà dei segnali naturali

Proprietà dei segnali naturali

Ogni segnale si può rappresentare con un vettore. Ad esempio, un segnale audio è un vettore unidimensionale, $\boldsymbol{x} = [x_1, x_2, \cdots, x_T]$, dove ciascuna componente rappresenta l’ampiezza della forma d’onda al tempo $t$. Prendiamo ad esempio il sistema uditivo umano. Per comprendere una persona mentre parla, la coclea converte la pressione d’aria delle vibrazioni sonore in impulsi nervosi, i quali vengono covertiti in linguaggio dal cervello tramite un modello linguistico in modo da selezionare l’enunciato più probabile dato il segnale. Per i segnali musicali, i segnali sono cosidetti stereofonici e hanno 2 o più canali (channels) in modo da creare l’illusione che il suono arrivi da più direzioni. Sebbene abbiano due canali, i segnali musicali sono comunque 1D perché lo stato del segnale è determinata solo da una sola variabile, il tempo.

Le immagini sono segnali 2D, perché l’informazione è raffigurata nello spazio bidimensionale. Ogni punto in questo spazio può essere a sua volta rappresentato con un vettore. Se abbiamo un’immagine con $d$ canali, ogni punto dell’immagine corrisponde ad un vettore di dimensione $d$. Una immagine a colori ha 3 canali RGB (RGB: Red, Green, Blue), quindi $d=3$. Per ciascun punto $x_{i,j}$, le componenti di questo vettore corrispondono all’intensità dei colori rosso, verde e blu.

Seguendo la stessa logica, si può rappresentare anche il linguaggio. Ogni parola corrisponde ad un vettore di componenti binarie (one-hot), che hanno valore uguale ad 1 in corrispondenza con la posizione in cui avviene la parola all’interno del nostro vocabolario, e valore uguale a 0 in tutte le altre posizioni. Dunque ogni parola è un vettore di dimensione uguale alla lunghezza del vocabolario.

I segnali naturali hanno le seguenti proprietà:

1. Stazionarietà: Alcuni motivi sono ripetuti attraverso il segnale. Nei segnali audio, possiamo osservare gli stessi schemi (pattern) ripetutamente lungo l’asse temporale. Nelle immagini, possiamo osservare pattern visivi simili in diverse posizioni nello spazio dell’immagine. <!– Natural data signals follow these properties:
2. Stationarity: Certain motifs repeat throughout a signal. In audio signals, we observe the same type of patterns over and over again across the temporal domain. In images, this means that we can expect similar visual patterns repeat across the dimensionality.–>
3. Localizzazione: I punti adiacenti hanno una maggiore correlazione fra di loro rispetto ai punti distanti l’uno dall’altro. Per un segnale 1D, ciò significa che osservando un picco ad un qualsiasi punto $t_i$, i punti che si trovano entro una piccola finestra da $t_i$ avranno molto probabilmente un valore simile al valore corrispondente a $t_i$, mentre per un punto $t_j$ che è lontano da $t_i$, $x_{t_i}$ sarà meno correlato con $x_{t_j}$. Più formalmente, la convoluzione tra un segnale e la sua versione rovesciata, raggiungono un picco quando il segnale si sovrappone perfettamente con la sua versione rovesciata. Una convoluzione fra due segnali 1D (o la loro correlazione incrociata) non è altro il loro prodotto scalare, che è una misura della similitudine fra due vettori, ovvero quanto sono distanti fra di loro. Quindi, l’informazione è contenuta in zone specifiche del segnale. Per le immagini, ciò vuol dire che la correlazione fra due punti diminuisce con l’aumentare della distanza fra di loro. Se il pixel $x_{0,0}$ è blu, la probabilità che il pixel accanto ($x_{1,0},x_{0,1}$) sia blu è piuttosto alta, ma se ci spostiamo verso il lato opposto dell’immagine, ($x_{-1,-1}$), il valore di questo pixel è indipendente del valore del pixel $x_{0,0}$.

1. Composizionalità: In natura, tutto è composto da parti, a loro volta composte di sottoinsiemi di parti, etc. Per esempio, i caratteri formano delle sequenze, che formano parole, che a loro volta formano frasi. Un insieme di frasi forma un testo (document). La composizionalità è ciò che ci permette di spiegare il mondo.

Se i nostri dati esibiscono queste proprietà di stazionarietà, localizzazione, e composizionalità, possiamo sfruttarle con reti che utilizzano sparsità, condivisione dei pesi e l’accatastamento di strati. <!–

1. Compositionality: Everything in nature is composed of parts that are composed of sub-parts and so on. As an example, characters form strings that form words, which further form sentences. Sentences can be combined to form documents. Compositionality allows the world to be explainable.

If our data exhibits stationarity, locality, and compositionality, we can exploit them with networks that use sparsity, weight sharing and stacking of layers.–>

Sfruttare le proprietà dei segnali naturali per ottenere invarianza ed equivarianza

Localizzazione $\Rightarrow$ sparsità

La Fig. 1 mostra una rete FC a 5 strati. Ogni freccia rappresenta un peso che viene moltiplicato con un input. Come possiamo vedere, questa rete è molto pesante dal punto di vista computazionale.

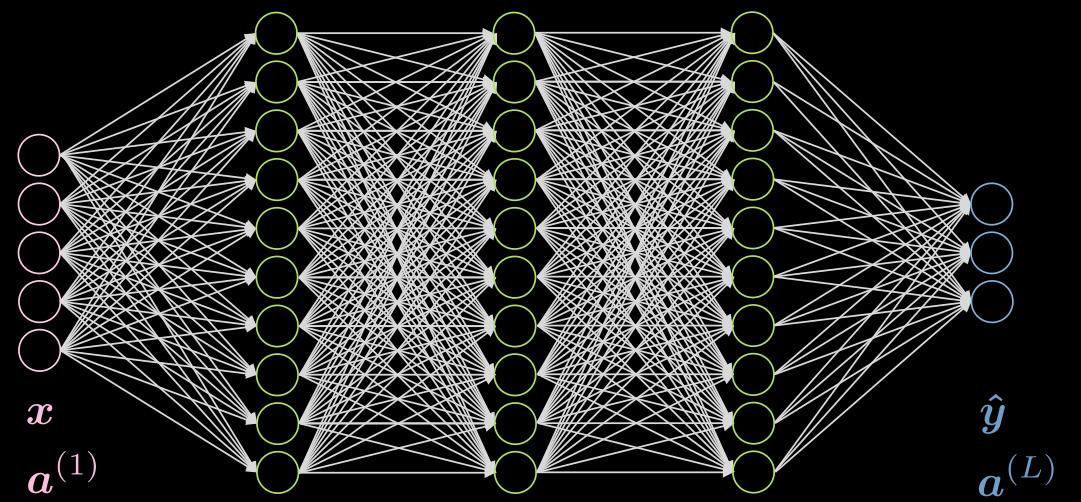
Fig. 1: rete FC (_Fully Connected_)

Se i nostri dati hanno la proprietà di localizzazione, possiamo connettere ciascun neurone ad un sottoinsieme “locale” di neuroni dello strato precedente. Quindi possiamo ignorare alcune connessioni come raffigurato nella Fig. 2. La Fig. 2(a) rappresenta una rete FC. Sfruttando la localizzazione dei dati, escludiamo le connessioni con i neuroni più distanti, come da Fig. 2(b). Seppure i neuroni dello strato nascosto (in verde) nella Fig. 2(b) non ricoprono completamente l’input, nell’insieme l’architettura considera ciascun neurone. Il campo recettivo (RF: receptive field) di uno strato è il numero di neuroni provenienti da uno strato precedente che vengono considerati dallo strato in questione. Dunque, il RF dell’output rispetto allo strato nascosto è di 3, il RF dello strato nascosto rispetto all’input è di 3, mentre il RF dell’output rispetto all’input è di 5.

Figure 2(a): prima della sparsificazione	Figure 2(b): dopo la sparsificazione

Stazionarietà $\Rightarrow$ condivisione dei pesi

Se i nostri dati hanno stazionarietà, possiamo riutilizzare un sottoinsieme di pesi/parametri più volte attraverso l’architettura della rete. Per esempio, nella rete sparsa di Fig. 3(a), possiamo condividere 3 pesi (giallo, arancione, e rosso). Di conseguenza, il numero di pesi diminuisce da 9 a 3! La nuova architettura può funzionare anche meglio perché i singoli pesi vengono addestrati su un maggior numero di dati. I pesi ottenuti con la sparsità e la condivisione dei pesi formano un filtro convoluzionale.

Fig. 3(a): senza condivisione dei pesi	Fig. 3(b): con condivisione dei pesi

I seguenti sono alcuni vantaggi dell’utilizzo della sparsità e della condivisione dei pesi:

• Condivisione dei pesi
  • convergenza più rapida
  • miglior generalizzazione
  • nessun vincolo sulla dimensione dell’input
  • indipendenza dei filtri $\Rightarrow$ alta capacità di parallelizzazione
• Sparsità delle connessioni
  • riduzione della computazione

La Fig. 4 mostra un esempio di filtro su dati 1D, dove la dimensione del filtro è: 2 (numero di filtri) * 7 (spessore dello strato precedente) * 3 (numero di pesi distinti).

La scelta della dimensione del filtro è empirica. I filtri convoluzionali 3 * 3 sembrano essere la dimensione minima per dati 2D. Una convoluzione di dimensione 1 può essere utilizzata per ottenere uno strato finale che può essere applicato ad una immagine input più grande. Se la dimensione del filtro è un numero pari potrebbe diminuire la qualità dei dati, quindi scegliamo sempre un kernel di dimensione dispari, generalmente 3 o 5.

| | | |Fig. 4(a): filtro su dati 1D | Fig. 4(b): dati con padding di zeri | –> <!– Fig. 4 shows an example of kernels on 1D data, where the kernel size is: 2(number of kernels) * 7(thickness of the previous layer) * 3(number of unique connections/weights).

The choice of kernel size is empirical. 3 * 3 convolution seems to be the minimal size for spatial data. Convolution of size 1 can be used to obtain a final layer that can be applied to a larger input image. Kernel size of even number might lower the quality of the data, thus we always have kernel size of odd numbers, usually 3 or 5.

| | | |Figure 4(a): kernels on 1D Data | Figure 4(b): data with Zero Padding| –>

Padding

Il padding (“imbottitura”) tende a inficiare i risultati finali, ma è conveniente per la programmazione. Generalmente utilizziamo padding di zeri: size = (kernel size - 1)/2. <!– ### Padding

Padding generally hurts the final results, but it is convenient programmatically. We usually use zero-padding: size = (kernel size - 1)/2.–>

CNN “spaziale” standard

Le CNN spaziali (nel senso che i dati hanno una relazione spaziale fra di loro) hanno le seguenti proprietà:

• Più di uno strato:
  • Convoluzione
  • Funzione nonlineare (ReLU e “Leaky-ReLU”)
  • Operazione di pooling
  • Normalizzazione del batch
• Bypass della connessione residua

La normalizzazione del batch e il bypass connessione residua sono molto utili per l’addestramento della rete. Se la rete è composta da troppi strati, alcune parti del segnale si possono perdere. Il bypass delle connessioni residue aggiungono ulteriori connessioni e garantiscono che ci sia un percorso attraverso la rete dal basso verso l’alto, nonché un percorso dall’alto verso il basso per i gradienti durante la retropropagazione.

Nella Fig. 5, vediamo che l’immagine di input contiene informazione principalmente nello spazio bidimensionale (a parte l’informazione caratteristica sul colore di ciascun pixel), mentre lo strato di output è spesso. Al centro, avviene uno scambio fra l’informazione spaziale e l’informazione caratteristica e la rappresentazione diventa più densa. Salendo nella gerarchia, otteniamo rappresentazioni sempre più dense e perdiamo l’informazione spaziale.

Pooling

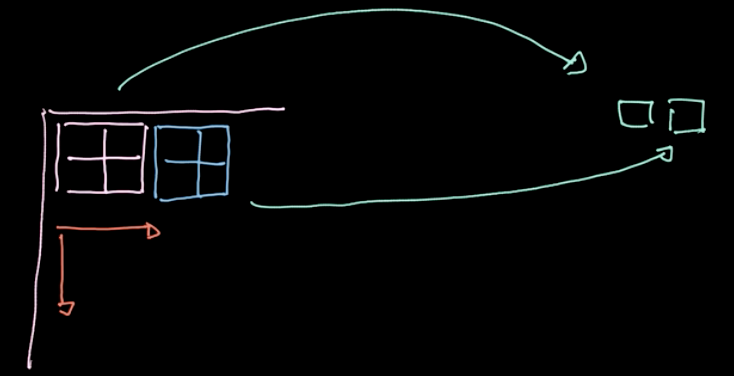
Fig. 6: raffigurazione dell'operazione di _pooling_

La norma $L_p$ viene calcolata su diverse regioni (come da Fig. 6). Questa operazione produce un valore per ciascuna regione (1 valore per 4 pixel nel nostro esempio). Procediamo con l’iterazione di questo processo regione per regione sull’intero dataset, spostando la regione a seconda del passo (stride) che abbiamo definito. Se i nostri dati hanno dimensione $m * n$ con $c$ canali, arriveremo ad un output con $\frac{m}{2} * \frac{n}{2}$, sempre con $c$ canali (come da Fig. 7). Il pooling non è regolato da un parametro nel nostro modello; tuttavia, possiamo scegliere diversi tipi di pooling come max-pooling, pooling della media (average pooling) etc. L’obiettivo principale del pooling è la riduzione del numero di dati, il che ci permette di compiere operazioni entro un tempo ragionevole.

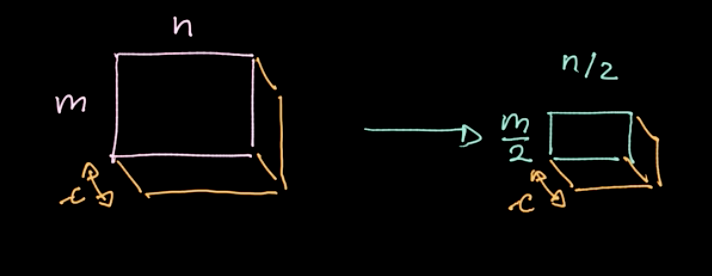
Fig. 7: risultato dell'operazione di _pooling_

CNN: Jupyter Notebook

Il Jupyter notebook si trova qui. Per eseguire il notebook, assicuratevi di aver installato ed attivato l’ambiente pDL come descritto nel README.md.

In questo notebook, addestreremo un percettrone multi-strato FC, ed ua rete neurale convoluzionale (CNN) per la classificazione sul dataset MNIST. Si noti che le reti hanno lo stesso numero di parametri. (Fig. 8)

Fig. 8: istanze del dataset MNIST originale

Prima dell’addestramento, normalizziamo i nostri dati, così che l’inizializzazione della nostra rete corrisponda alla distribuzione dei dati (molto importante!). Inoltre, assicuratevi di aver compiuto le seguenti operazioni/passi nella fase di addestramento:

1. Introdurre i dati al modello
2. Calcolare l’errore
3. Svuotare la cache dei gradienti accumulati, utilizzando zero_grad()
4. Calcolare i gradienti
5. Operare un passo del metodo di ottimizzazione

Prima di tutto, addestreremo entrambe le reti sui dati MNIST normalizzati. L’accuratezza della rete FC è $87\%$, mentre l’accuratezza della CNN è $95\%$. Dato lo stesso numero di parametri, la CNN è riuscita ad addestrare molti più filtri. Nella rete FC tutti quei filtri che provano a rappresentare relazioni fra pixel distanti fra di loro vengono addestrati invano, sono quindi sprecati. Invece, nella rete convoluzionale, tutti questi parametri si concentrano sul rilevare le relazioni fra pixels vicinanti.

Dopodiché, eseguiamo una permutazione casuale di tutti i pixel nelle immagini del nostro dataset MNIST. Ciò trasforma i dati dalla raffigurazione in Fig. 8 a quella di Fig. 9. Poi addestriamo entrambe le reti su questo dataset modificato.

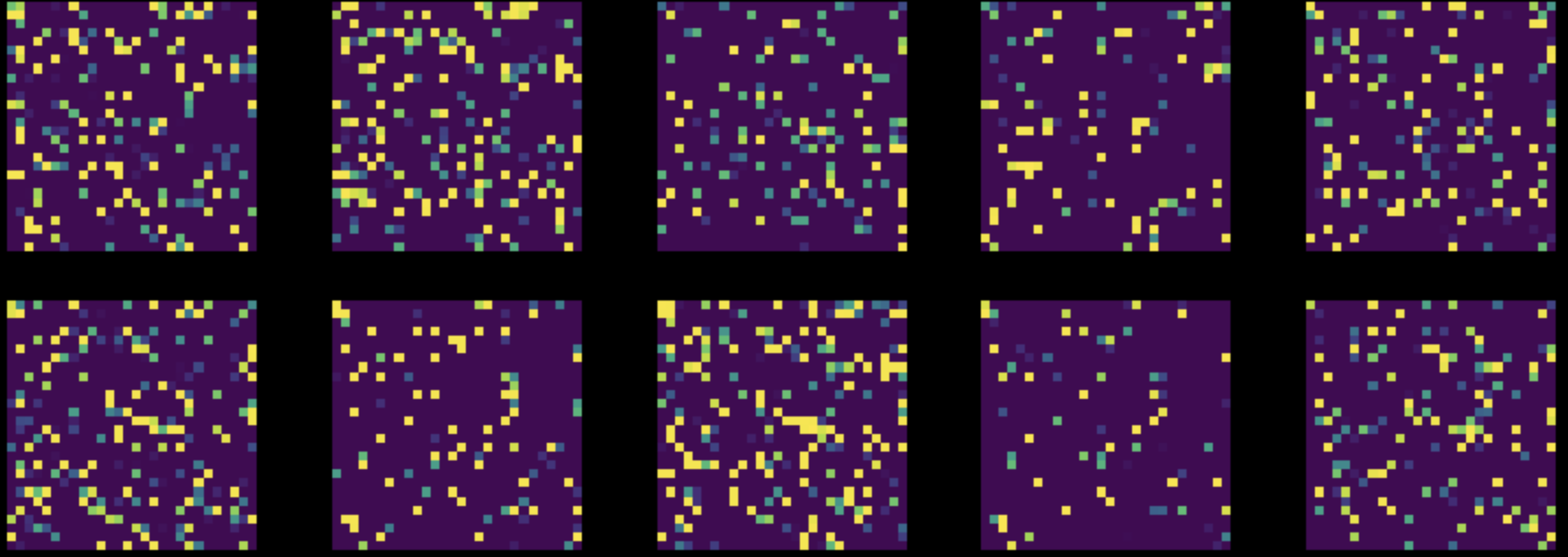
Fig. 9: istanze del dataset MNIST permutato

L’accuratezza della rete FC è rimasta più o meno uguale ($85\%$), mentre quella della CNN è scesa a $83\%$. Questo perché la permutazione casuale dei dati ha eliminato le tre proprietà di localizzazione, stazionarietà, e composizionalità, che le CNN possono sfruttare al meglio.