Evoluzione, architetture, implementazione dettagliata e vantaggi delle CNN

Evoluzione delle CNN da prototipo alle CNN moderne

Prototipo di reti neurali convoluzionali su piccoli dataset

Prendendo ispirazione dal lavoro di Fukushima sui modelli della corteccia visiva, Yann LeCun sviluppò la prima rete neurale convoluzionale (CNN) all’Università di Toronto nel ‘88-‘89, utilizzando una gerarchia di cellule semplici/complesse insieme all’addestramento supervisionato e la retropropagazione. Gli esperimenti utilizzarono un piccolo dataset di 320 cifre. La performance delle seguenti architetture furono messe a confronto:

1. Strato unico totalmente connesso (FC: fully connected)
2. Due strati FC
3. Strati connessi localmente senza pesi condivisi
4. Rete vincolata con pesi condivisi e connessioni localizzate
5. Rete vincolata con pesi condivisi e connessioni localizzate (con più mappe delle caratteristiche, o feature maps)

Le reti con maggiore successo (reti vincolate con pesi condivisi) avevano una maggiore capacità di generalizazione, e formarono la base per le CNN moderne. Il modello con un unico strato FC, invece, tende a sovradattare (overfitting).

Le prime “vere” CNN a Bell Labs

Dopo essersi spostato a Bell Labs, la ricerca di LeCun passò all’utilizzo di codici postali scritti a mano dal servizio postale statunitense per l’addestramento di una CNN più grande:

• 257 (16$\times $16) strati di input
• 12 filtri (5$\times $5) con passo (stride) di 2 (avanzamento di 2 pixel): il prossimo strato avrà una risoluzione inferiore
• SENZA operazione di pooling

Architettura di reti convoluzionali con pooling

L’anno successivo, si fecero alcuni cambiamenti: venne introdotto uno strato di pooling separato. Lo strato di pooling calcola la media dei valori dell’input, aggiungendo un termine costante (bias), e passandola ad una funzione non lineare (funzione tangente iperbolica). Venne applicato uno strato di pooling di dimensione $2\times2$ e passo di 2, dimezzando cosí le risoluzioni.

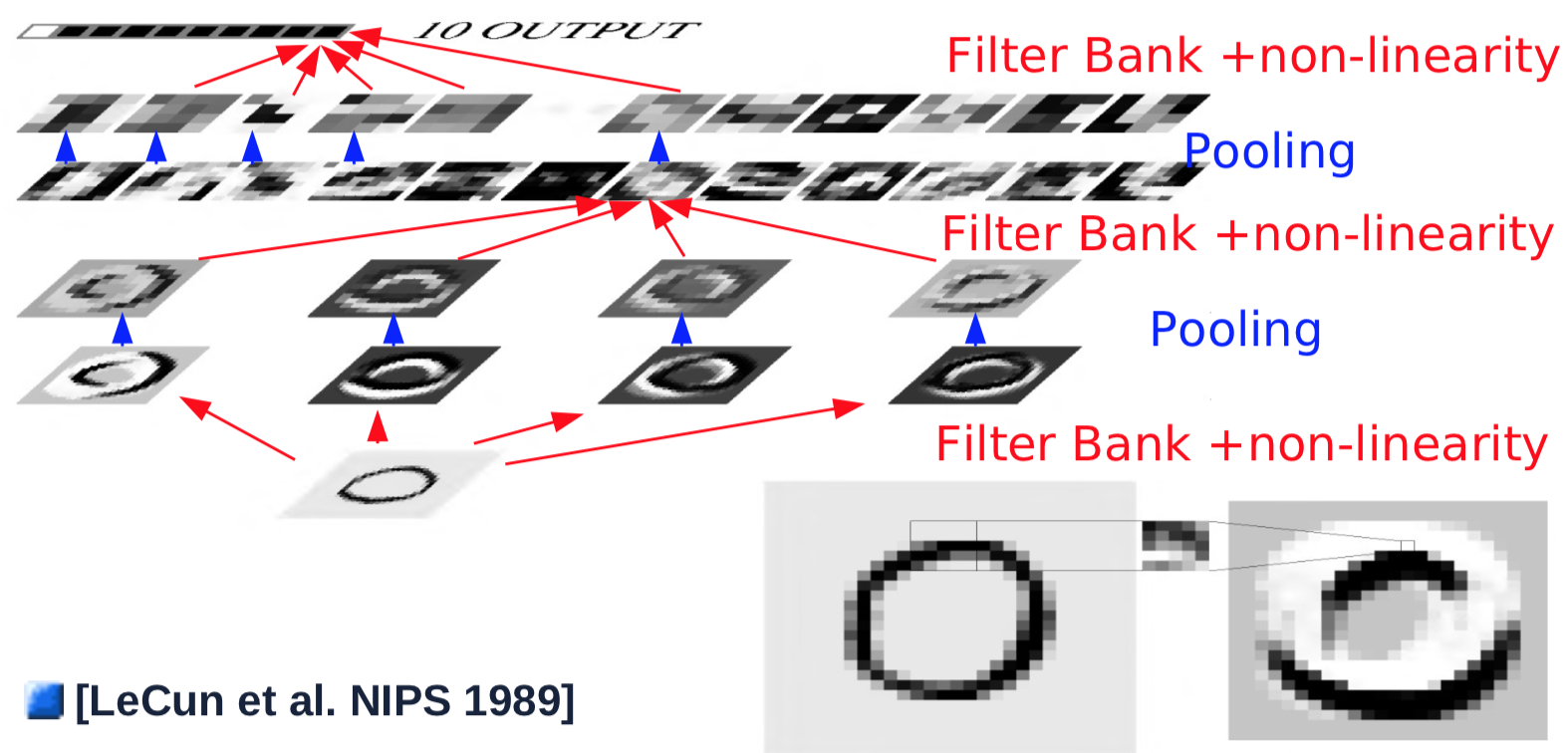
Fig. 1 Architettura di una rete convoluzionale

Il seguente è un esempio di una rete con un solo strato convoluzionale:

1. Si consideri un input di dimensione 32$\times$32
2. Lo strato convoluzionale passa un filtro di dimensione 5$\times$5 con passo di 1 sull’immagine, creando una mappa delle caratteristiche di dimensione 28$\times$28
3. Si passa la mappa delle caratteristiche ad una funzione non lineare: dimensione 28$\times$28
4. Si passa ad uno strato di pooling, che calcola la media su una finestra di dimensione 2$\times$2 con passo 2: dimensione 14$\times$14
5. Si ripetono 1-4 per ciascuno dei 4 filtri

Generalmente il primo strato, fatto di semplici combinazioni di convoluzioni/pooling, riconosci caratteristiche semplici, come bordi orientati. Dopo il primo strato di convoluzioni/pooling, l’obiettivo è riconoscere combinazioni di caratteristiche dagli strati precedenti. Per ottenere questo si ripetono i punti 2-4, passando diversi filtri sulle mappe delle caratteristiche degli strati precedenti, che vengono poi sommati per formare una nuova mappa delle caratteristiche:

1. Si passa un nuovo filtro 5$\times$5 su ciascuna mappa delle caratteristiche dagli strati precedenti e si sommano i risultati (nota: nell’esperimento del 1989 del prof. LeCun, si omettono alcuni strati per motivi computazionali. Le configurazioni moderne generalmente impongono che la rete sia completamente connessa): dimensione 10$\times$10
2. Si passa il risultato dello strato convoluzionale ad una funzione non lineare: dimensione 10$\times$10.
3. Si ripetono 1-2 per ciascuno dei 16 filtri.
4. Si passa il risultato ad uno strato di pooling, che calcola la media su una finestra di dimensione 2$\times$2 con passo 2: dimensione 5$\times$5 per ogni mappa delle caratteristiche.

Per generare un output, l’ultimo strato convoluzionale somiglia ad una connessione completa (FC):

1. L’ultimo strato convoluzionale passa un filtro 5$\times$5 sopra l’intera mappa delle caratteristiche, le quali vengono sommate, risultando in una matrice di dimensione 1$\times$1
2. Si passa il risultato ad una funzione non lineare: dimensione 1$\times$1.
3. Si genera un singolo output per la categoria in questione.
4. Si ripetono i passi precedenti per ciascuna delle 10 cateogrie (in parallelo).

Si veda Questa animiazione sul sito di Anrej Karpathy su come le convoluzioni cambiano la dimensione della mappa delle caratteristiche dello strato successivo. L’articolo completo è disponibile qui.

Equivarianza rispetto alla traslazione

Fig. 2 Equivarianza rispetto alla traslazione

Come dimostrato dall’animazione sulle slide (questo è un’altro esempio), la translazione dell’input risulta nella stessa traslazione della mappa delle caratteristiche. Tuttavia, le variazioni nella mappa delle caratteristiche vengono dilatate o contratte rispetto alle operazioni di convoluzione/pooling. Per esempio, se si ha uno strato di pooling 2$\times$2 e passo 2, una traslazione di 1 pixel dell’input risulta in una traslazione di 0.5 pixel delle mappe delle caratteristiche successive. La risoluzione viene quindi “scambiata” per avere un maggior numero di tipi di caratteristiche, ovvero per rendere la rappresentazione più astratta e meno sensibile a traslazioni e distorsioni.

Struttura generale dell’architettura

La struttura generale dell’architettura delle CNN si può suddividere in vari strati archetipo:

• Normalizzazione
  • Aggiustamento dello whitening (facoltativo)
  • Metodi sottrattivi, ad esempio sottrazione della media, filtro passa-alto
  • Metodi divisivi: normalizzazione del contrasto locale, normalizzazione della varianza
• Filter Banks
  • Aumento della dimensione
  • Proiezione su una base completa
  • riconoscizione bordi
• Funzioni non lineari
  • Dispersione
  • Tipicamente si utilizza un rettificatore, o unità lineare rettificata (ReLU: Rectified Linear Unit): $\text{ReLU}(x) = \max(x, 0)$
• Pooling
  • Raggruppamento su una mappa delle caratteristiche

  • Max Pooling: $\text{MAX}= \text{Max}_i(X_i)$

  • Pooling con norma-LP: $\text{L}p= \left(\sum_{i=1}^n |X_i|^p \right)^{\frac{1}{p}}$

  • Pooling con probabilità su scala logaritmica: $\text{Prob}= \frac{1}{b} \left(\sum_{i=1}^n e^{b X_i} \right)$

LeNet5 e il riconoscimento delle cifre

Implementazione di LeNet5 con PyTorch

LeNet5 consiste dei seguenti strati (elecanti dall’alto al basso):

1. Log-softmax
2. Strato FC di dimensione 500$\times$10
3. ReLU
4. Strato FC di dimensione 4$\times$4$\times$50)$\times$500
5. Max Pooling di dimensione 2$\times$2, passo di 2.
6. ReLu
7. Convoluzione con 20 canali output, filtro 5$\times$5 e passo di 1.
8. Max Pooling di dimensione 2$\times$2, stride di 2.
9. ReLu
10. Convoluzione con 20 canali output, filtro 5$\times$5, passo di 1.

LeNet5 si può implementare con Pytorch con il seguente codice:

class LeNet5(nn.Module):
    def __init__(self):
        super().__init__()
        self.conv1 = nn.Conv2d(1, 20, 5, 1)
        self.conv2 = nn.Conv2d(20, 20, 5, 1)
        self.fc1 = nn.Linear(4*4*50, 500)
        self.fc2 = nn.Linear(500, 10)

    def forward(self, x):
    x = F.relu(self.conv1(x))
    x = F.max_pool2d(x, 2, 2)
    x = F.relu(self.conv2(x))
    x = F.max_pool2d(x, 2, 2)
    x = x.view(-1, 4*4*50)
    x = F.relu(self.fc1)
    x = self.fc2(x)
    return F.logsoftmax(x, dim=1)

Anche se fc1 e fc2 sono strati completamente connessi (FC), si possono consdierare come strati convoluzionali con filtri che ricoprono l’intero input. Gli strati FC vengono utilzizati per motivi di efficenza.

Lo stesso codice si può scrivere utilizzando nn.Sequential, ma questo metodo è obsoleto.

Vantaggi delle CNN

In una rete completamente convoluzionale, non vi è bisogno di specificare le dimensioni dell’input. Tuttavia, cambiare la dimensione dell’input cambia la dimensione dell’output.

Si consideri un sistema di riconoscimento di testo scritto a mano in cosrivo. Non è necessario segmentare l’immagine input. Basta utilizzare una CNN sull’immagine intera: i filtri copriranno ogni posizione sul’immagine intera e produrranno lo stesso output indipendentemente dalla posizione in cui è stato riconoscito lo schema (pattern). Applicare la CNN ad un’immagine intera è molto meno costoso che applicarla su diverse posizioni separatamente. Non è necessaria una segmentazione iniziale, il che è un sollievo perché la segmentazione di un’immagine è simile al riconosimento di un immagine.

Esempio: MNIST

La LeNet5 è stata addestrata su immagini 32$\times$32 di MNIST per classificare cifre individuali al centro di un’immagine. Si utilizzò una technica di aumento dei dati (data augmentation), spostando le cifre, cambiando la dimensione delle cifre, ed inserendo altre cifre a fianco. Fu anche addestrato utilizzando un’undicesima categoria, per rappresentare cifre che non corrispondevano alle 10 cifre precedenti. Le immagini etichettate (labeled) da questa categorie erano generate producendo immagini vuote, oppure collocando le cifre ai lati invece che al centro dell’immagine.

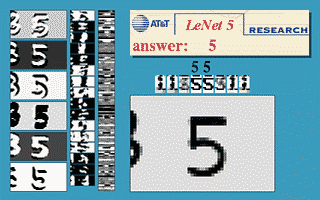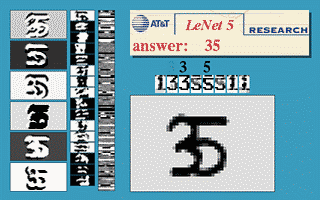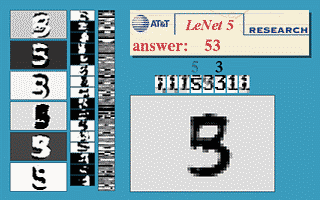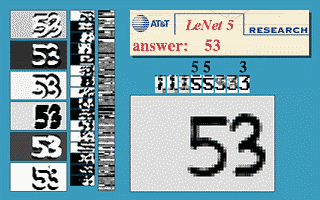
Fig. 3 Finestra Scorrevole di una CNN

L’immagine qui sopra dimostra che una rete LeNet5 addestrata su immagini 32$\times$32 può essere utilizzata su un’immagine input 32$\times$64 per riconoscere cifre in diverse posizioni.

Problema della combinazione delle caratteristiche

Che cos’è il problema della combinazione delle caratteristiche?

I neuroscienziati visivi e gli esperti di visione artificiale affrontano il problema di definire un oggetto come tale. Un oggetto è una collezione di caratteristiche, ma come si possono combinare tutte le caratteristiche per costruire l’oggetto in questione?

Come si risolve?

Possiamo risolvere il problema della combinazione delle caratteristiche utilizzando una semplice CNN: bastano solo due strati convoluzionali con pooling e altri due strati FC senza meccanismi specifici, ponendo che si abbiamo abbastanza funzioni non lineari e dati per addestrare la rete.

Fig. 4 CNN per risolvere il problema dell'unione delle caratteristiche

L’animazione qui sopra mostra la capacità delle CNN nel riconoscere le cifre tramite lo spostamento di un unico tratto, dimostrando come risolvono il problema della combinazione delle caratteristiche, riconoscendo le caratteristiche in maniera gerarchica e compositiva.

Esempio: input di lunghezza dinamica

Possiamo costruire una CNN con due strati convoluzionali con passo 1 e due strati pooling con passo 2 in modo che il passo totale sia 4. Cosí, per ottenere un nuovo output bisogna traslare la finestra di input di 4. Si può vedere ciò in maniera più esplicativa dalla figura seguente (unità verdi). Iniziamo con un input di dimensione 10, si realizza una convoluzione di dimensione 3 per ottenere 8 unità. Dopodiché, si realizza il pooling di dimensione 2 per ottenere 4 unità. Come prima, si ripetono le operazioni di convoluzione e pooling fino ad ottenere 1 unità di output.

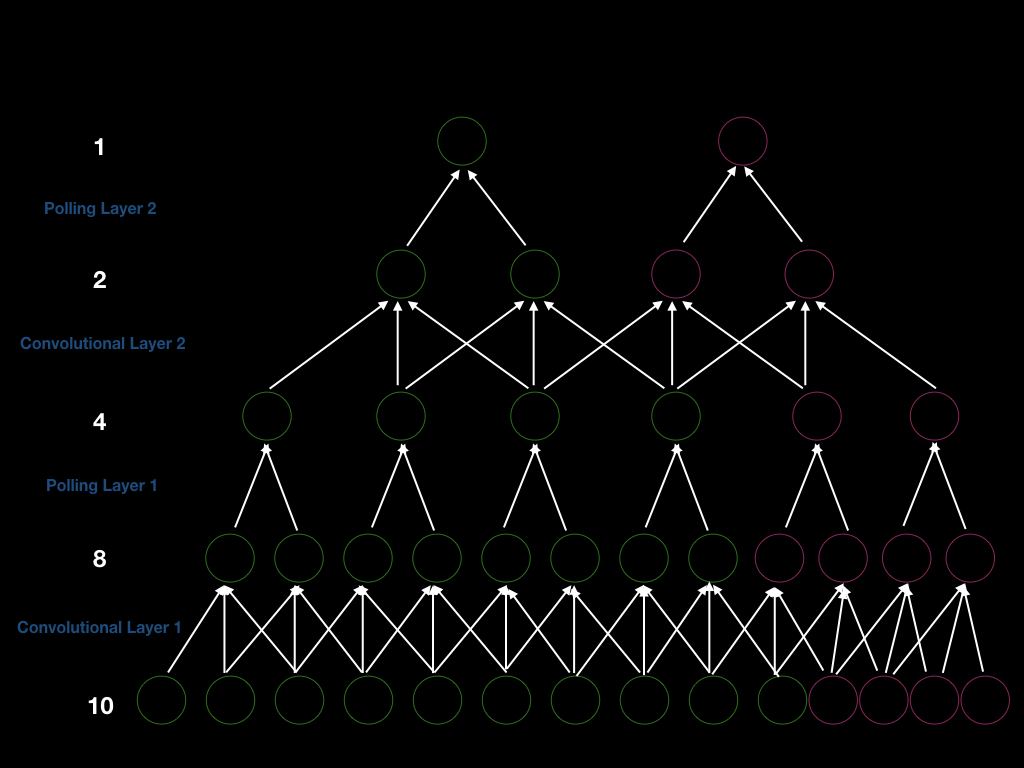
Fig. 5 Architettura CNN su unione di input con lunghezza variabile

Assumiamo di aggiungere 4 unità allo strato input (unità rosa nella figura qui sopra) in modo da ottenere 4 unità in più dopo il primo strato convoluzionale, 2 unità in più dopo la prima operazione di pooling, 2 unità in più dopo il secondo strato convoluzionale e 1 unità in più nell’output. Di consequenza, la dimensione della finestra per generare un nuovo output dovrà essere 4 (passo di 2 $\times$2). Inoltre, questo indica che aumentando la dimensione dell’input si aumenta la dimensione di ciascuno strato, mostrando che le CNN riescono a gestire input con lunghezza dinamica.

A quale tipo di segnali si prestano le CNN?

Le CNN si prestano bene a segnali sottoforma di matrici multidimensionali con le seguenti proprietà:

1. Localizzazione: La prima (proprietà) è che esistono forti correlazioni “localizzate” fra i valori. Se prendiamo due pixel di un’immagine naturale, è molto probabile che questi due pixel avranno lo stesso colore. Con l’aumentare della distanza fra due pixel, la somiglianza fra di loro diminuirà. Queste correlazioni localizzate fra pixel ci permettono di riconoscere caratteristiche locali, che è ciò che fanno le CNN. Se diamo dei pixel permutati come input ad una CNN, questa non riconoscerebbe altrettanto bene l’immagine, mentre non ci sarebbero differenze con una rete FC. Le correlazioni localizzate giustificano l’utilizzo di connessioni localizzate.

2. Stazionarietà: La seconda proprietà è che le caratteristiche sono essenziali e possono apparire ovunque sull’immagine, giustificando l’utilizzo dei pesi condivisi e del pooling. Inoltre, i segnali statistici seguono una distribuzione uniforme, quindi bisogna ripetere il riconoscimento delle caratteristiche per ogni posizione sull’immagine input.
3. Composizionalità: La terza proprietà è che le immagini naturali sono compositive, quindi le caratteristiche formano un’immagine in maniera gerarchica. Questo giustifica l’utilizzo di più strati di neuroni, che oltretutto ricalca i risultati della ricerca di Hubel e Weisel sulle cellule semplici e complesse.

Inoltre, le CNN vengono usate su video, immagini, testi e riconoscimento vocale.