Visualizzazione delle trasformazioni dei parametri delle reti neurali e concetto fondamentale di convoluzione

Visualizzazione di reti neurali

In questa sezione visualizzeremo il funzionamento interno di una rete neurale

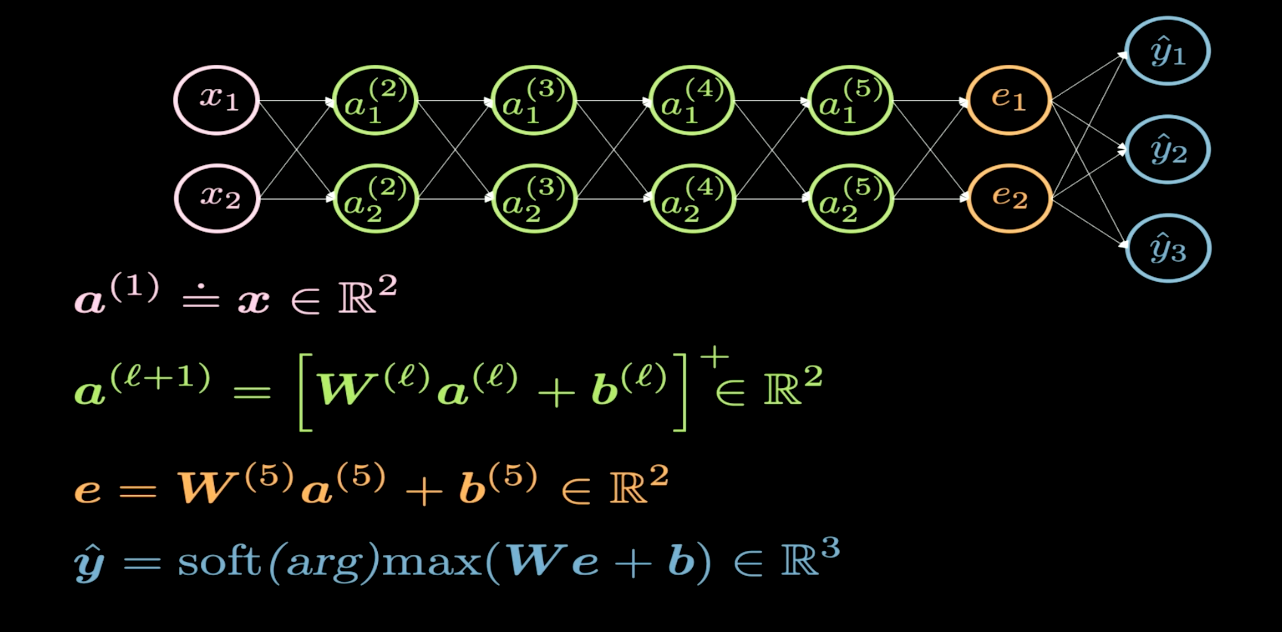
Fig. 1 Struttura di una rete neurale

La Fig. 1 mostra la struttura della rete neurale che vorremmo visualizzare. Normalmente, quando disegniamo la struttura di una rete neurale, l’input viene fatto comparire in basso oppure a sinistra e l’output in alto oppure a destra. Nella Fig. 1, i neuroni rosa rappresentano l’input e i blu rappresentano l’output. In questa rete, abbiamo 4 strati nascosti (in verde), il che significa che abbiamo 6 strati in totale (4 strati nascosti + 1 strato di input + 1 strato di output). In questo caso, abbiamo 2 neuroni per strato nascosto, quindi la dimensione della matrice dei pesi ($W$) per ogni strato è 2x2. Ciò perché vogliamo trasformare il nostro piano di input in un altro piano che vogliamo poter visualizzare.

Fig. 2 Visualizzazione del ripiegamento dello spazio

Trasformare uno strato è come ripiegare il nostro piano in qualche specifica regione, come mostrato in Fig. 2. Questo ripiegamento è molto brusco, perché tutte le trasformazioni sono applicate nello strato 2D. In questo esperimento, notiamo che, se abbiamo solo 2 neuroni per strato nascosto, l’ottimizzazione sarà più lenta; l’ottimizzazione è più semplice se abbiamo più neuroni per strato nascosto. Ciò ci lascia con un’importante domanda da considerare: perché è più difficile addestrare la rete con meno neuroni negli strati nascosti? Dovresti ponderare tu stesso su questa domanda e ci ritorneremo sopra dopo la visualizzazione del $\texttt{ReLU}$.

(a)	(b)

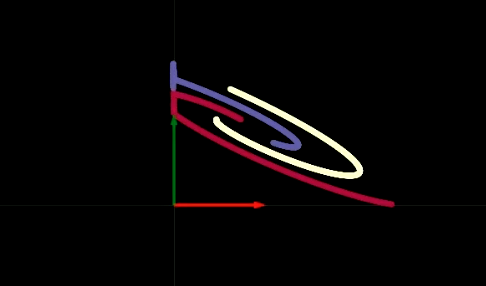
Quando navighiamo attraverso la rete, uno strato nascosto alla volta, vediamo che all’interno di ogni strato effettuiamo delle trasformazioni affini seguite dall’applicazione dell’operazione nonlineare ReLU, che elimina ogni valore negativo. Nelle Figure 3(a) e (b), possiamo vedere una visualizzazione dell’operatore ReLU. Quest’ultimo ci aiuta ad effettuare trasformazioni nonlineari. Dopo varie applicazioni di trasformazioni affini seguite dall’operatore ReLU, siamo finalmente in grado di separare linearmente i dati, come possiamo vedere in Fig. 4.

Fig. 4 Visualizzazione degli output

Ciò ci fornisce delle intuizioni sul perché gli strati nascosti sono più difficili da addestrare. La nostra rete composta da 6 strati ha un neurone di bias per ogni strato nascosto; quindi, se uno di questi bias muove i punti al di fuori del quadrante in alto a destra, l’applicazione dell’operatore ReLU appiattirà questi punti a zero. Dopo di ciò, indipendentemente da come gli strati successivi trasformeranno i dati, i valori rimarranno sempre zero. Possiamo concepire una rete neurale che sia più facilmente addestrabile rendendola più spessa, ovvero aggiungendo più neuroni negli strati nascosti, oppure possiamo aggiungere più strati nascosti, o ancora una combinazione dei due. Attraverso questo corso esploreremo come determinare le migliori architetture delle reti per un dato problema, rimanete sul pezzo.

Trasformazioni dei parametri

Trasformare in maniera generica i parametri significa che il nostro vettore dei parametri $w$ è l’output di una funzione. Per mezzo di questa trasformazione, possiamo mappare lo spazio dei parametri originario in un altro spazio. In Fig. 5, $w$ è l’output di $H$ applicato al parametro $u$. $G(x,w)$ è una rete e $C(y, \bar y)$ è una funzione di costo. La formula della retropropagazione è anch’essa adattata come segue:

Queste formule sono applicate in forma matriciale. Si noti che la dimensione dei termini dev’essere coerente. Le dimensioni di $u$, $w$, $\frac{\partial H}{\partial u}^\top$, $\frac{\partial C}{\partial w}^\top$ sono, rispettivamente, $[N_u \times 1]$, $[N_w \times 1]$, $[N_u \times N_w]$, $[N_w \times 1]$; quindi, la dimensione della nostra formula di retropropagazione è coerente.

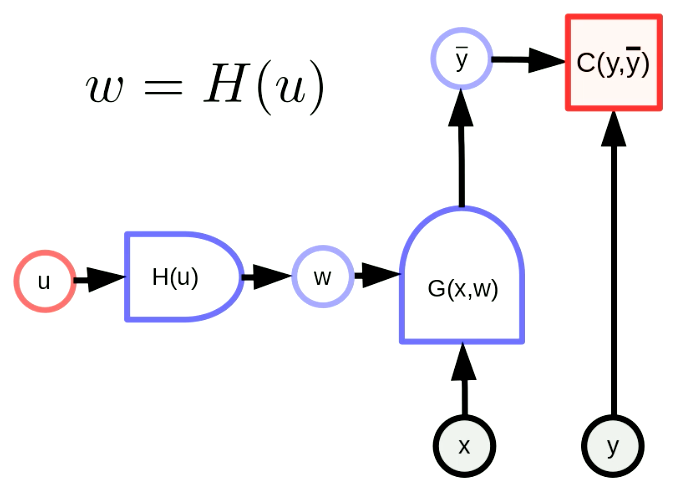
Fig. 5 Forma generica delle trasformazioni dei parametri

Una semplice trasformazione dei parametri: la condivisione dei pesi

Condivisione dei pesi significa semplicemente che $H(u)$ replica un componente di $u$ in più componenti di $w$. $H(u)$ è come un ramo a Y per copiare $u_1$ in $w_1$ e $w_2$. Ciò è esprimibile come

Forziamo i parametri condivisi ad essere uguali, così che il gradiente nei confronti dei parametri condivisi sarà sommato nella retropropagazione. Per esempio, il gradiente della funzione di costo $C(y, \bar y)$ rispetto a $u_1$ sarà la somma gradiente della funzione di costo $C(y, \bar y)$ rispetto a $w_1$ e il gradiente della funzione di costo $C(y, \bar y)$ rispetto a $w_2$.

Hypernetwork

Una hypernetwork è una rete nella quale i pesi di una rete sono l’output di un’altra rete. La Fig. 6 mostra il grafo computazionale di una hypernetwork. Qui la funzione $H$ è una rete con vettore dei parametri $u$ e input $x$. Il risultato di ciò è che i pesi di $G(x,w)$ sono configurati in maniera dinamica dalla rete $H(x,u)$. Nonostante questa sia un’idea datata, rimane molto potente.

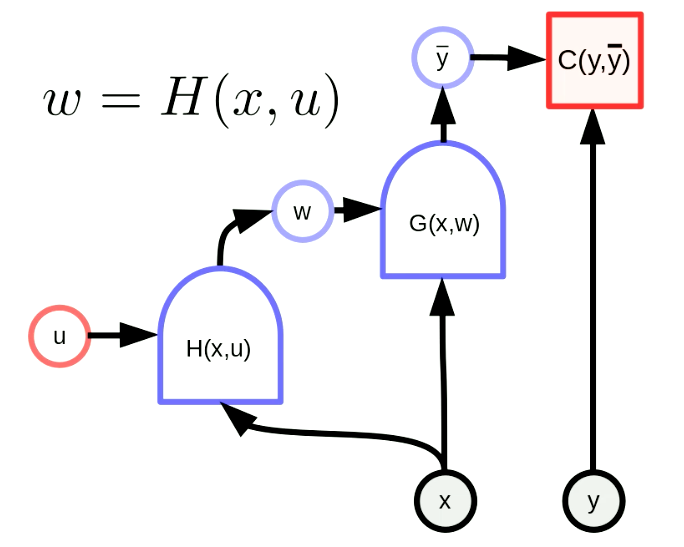
Fig. 6 *Hypernetwork*

Riconoscimento di pattern in dati sequenziali

La condivisione dei pesi può essere applicata al riconoscimento di pattern (pattern recognition), ovvero all’operazione di trovare dei pattern ricorrenti in dati sequenziali, come parole chiave in segnali vocali o spezzoni di testo. Un modo per ottenere ciò, come si può vedere in Fig. 7, è tramite l’utilizzo di una finestra scorrevole sui dati, la quale finestra muove la funzione di condivisione pesi per rilevare un particolare pattern (es. un suono particolare in un segnale vocale), e l’output viene passato ad una funzione di massimo.

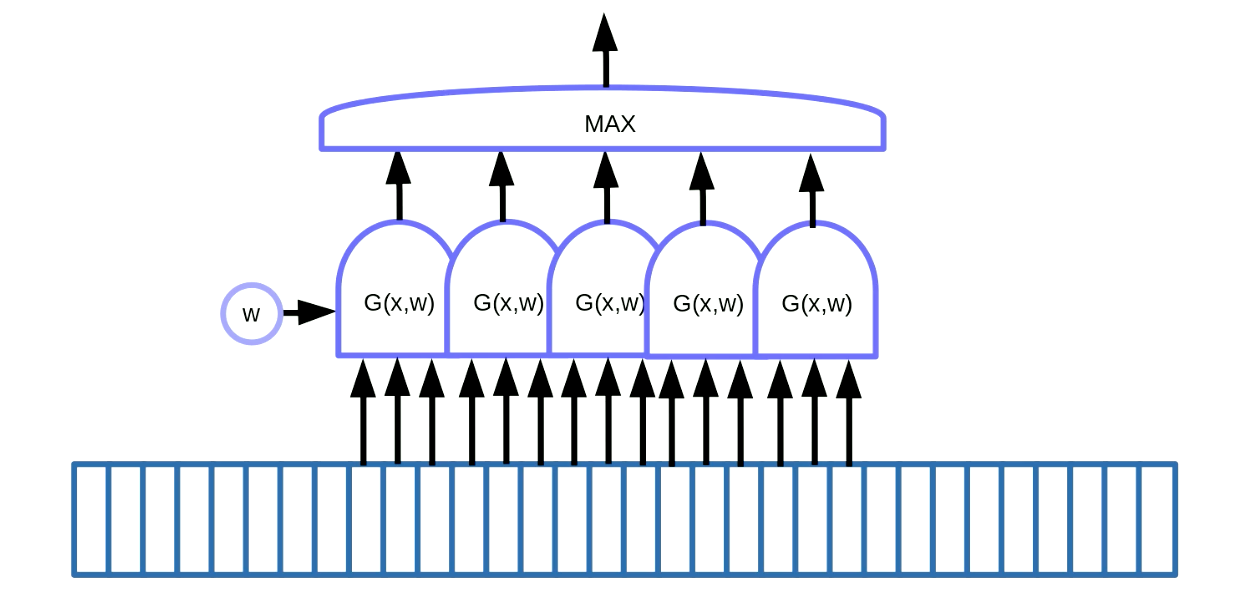
Fig. 7 *Riconoscimento di motivi* per dati sequenziali

In questo esempio abbiamo 5 di tali funzioni. Come risultato di questa soluzione, sommiamo cinque gradienti e retropropaghiamo l’errore per aggiornare il parametro $w$. Quando implementiamo ciò in PyTorch, vogliamo prevenire l’implicita accumulazione di questi gradienti, quindi dobbiamo usare zero_grad() per inizializzare il gradiente.

Riconoscimento di motivi in immagini

Un’altra applicazione utile è il riconoscimento di motivi nelle immagini. Normalmente, facciamo passare una “sagoma” sopra le immagini per riconoscere delle forme indipendentemente dalla posizione e dalla distorsione delle forme. Un semplice esempio è dato dal distinguere fra le lettere “C” e “D”, come da Fig. 8. La differenza fra “C” e “D” è che la “C” ha due estremità, mentre la “D” ha due angoli; in questo modo, possiamo progettare “sagome” per le estremità e sagome per gli angoli. Se la forma è simile a quella delle sagome, darà degli output limitati. Possiamo quindi distinguere le due lettere da tali output sommando questi ultimi. Nella Fig. 8, la rete riconosce due estremità a zero angoli, di conseguenza attiva “C”.

È anche importante che il nostro “rilevatore di sagome” sia invariante rispetto alle traslazioni - quando trasliamo l’input, l’output (es. le lettere rilevate) non dovrebbe cambiare. Ciò può essere risolto con la condivisione dei pesi. Come da Fig. 9, quando cambiamo la posizione della “D”, possiamo ancora riconoscere i motivi degli angoli nonostante siano stati traslati. Quando sommiamo i motivi, si attiverà il riconoscimento della “D”. <!–

Motif detection in images

The other useful application is motif detection in images. We usually swipe our “templates” over images to detect the shapes independent of position and distortion of the shapes. A simple example is to distinguish between “C” and “D”, as Figure 8 shows. The difference between “C” and “D” is that “C” has two endpoints and “D” has two corners. So we can design “endpoint templates” and “corner templates”. If the shape is similar to the “templates”, it will have thresholded outputs. Then we can distinguish letters from these outputs by summing them up. In Figure 8, the network detects two endpoints and zero corners, so it activates “C”.

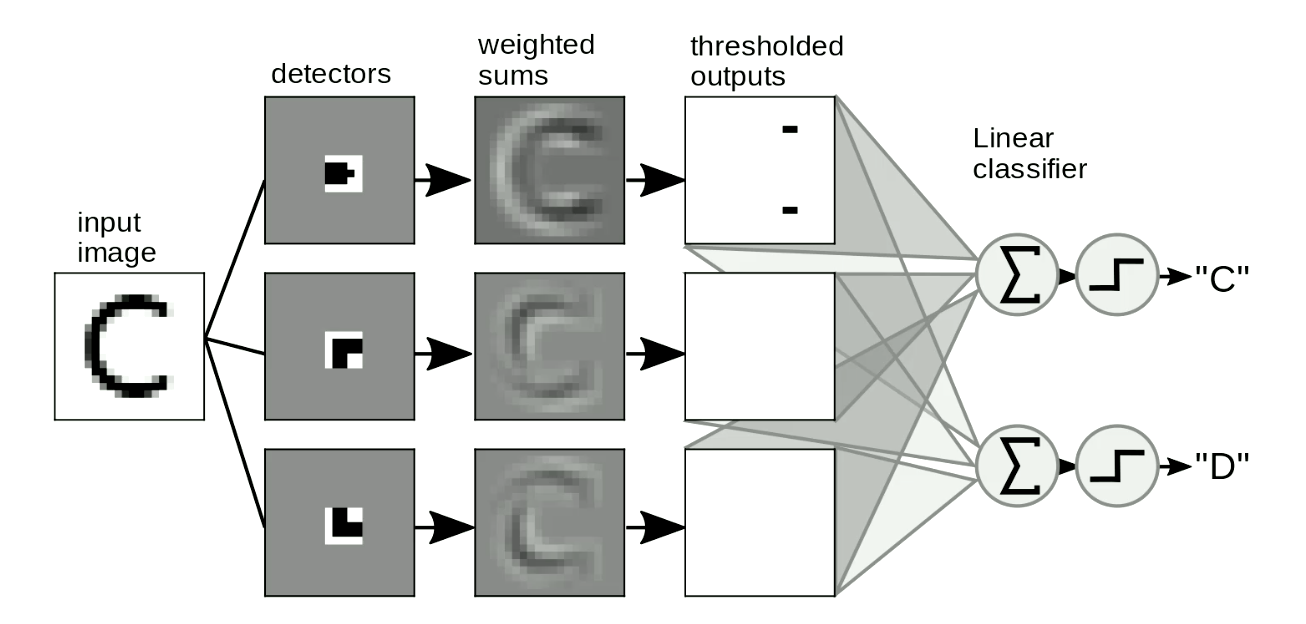
Fig. 8 Motif Detection for Images

–>

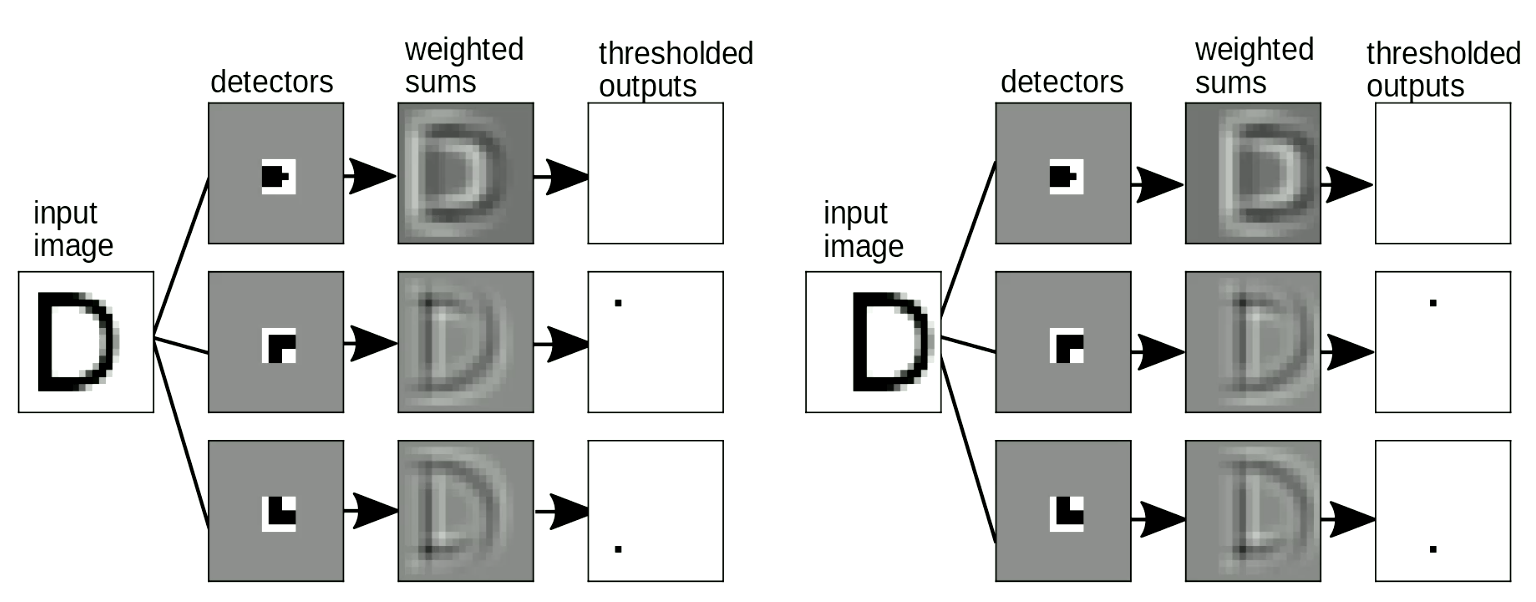
Fig. 9 Invarianza rispetto alle traslazioni

Questo metodo “artigianale” che utilizza rilevatori locali e somme per il riconoscimento delle cifre è stato utilizzato per molti anni. Ma ci pone il seguente problema: come possiamo progettare queste “sagome” automaticamente? Possiamo usare reti neurali per apprenderle? Adesso, presenteremo il concetto di convoluzione, cioè, l’operazione che utilizziamo per confrontare immagini con “sagome”.

Convoluzione discreta

Convoluzione

La definizione matematica precisa di convoluzione fra l’input $x$ e $w$ nel caso unidimensionale è:

A parole, l’output $i$-esimo è calcolato come il prodotto vettoriale fra $w$ rovesciato e una finestra di $x$ della stessa dimensione di $w$. Per ottenere l’output completo, facciamo partire la finestra dall’inizio di $x$, la trasliamo di 1 unità per ogni componente di $x$ e continuiamo finché non vi sono più termini rimasti.

Correlazione incrociata

In pratica, la convenzione adottata nelle strutture di apprendimento profondo come PyTorch è leggermente diversa. La convoluzione in PyTorch è implementata così che $w$ non sia rovesciato:

I matematici chiamano questa formulazione “correlazione incrociata” (cross-correlation). Nel nostro contesto, questa differenza è solamente una divergenza a livello di convenzioni. In pratica, la correlazione incrociata e la convoluzione possono essere intercambiabili se la lettura dei pesi conservati nella memoria avviene in maniera sequenziale in avanti oppure indietro.

Essere al corrente di questa differenza è importante, per esempio, quando si vuole fare uso di certe proprietà matematiche delle convoluzioni/correlazioni da testi matematici.

Convoluzione in più dimensioni

Per input bidimensionali come le immagini, facciamo uso della versione in due dimensioni della convoluzione:

Questa definizione può essere estesa senza problemi a tre o quattro dimensioni. Qui $w$ prende il nome di filtro convoluzionale (convolution kernel).

Modifiche classiche che possono essere effettuate con l’operazione di convoluzione nelle DCNN

1. Passo (stride): anziché traslare la finestra in $x$ di una componente alla volta, si può traslarla con un passo maggiore (ad esempio, due o tre componenti alla volta). Esempio: supponiamo che l’input $x$ sia monodimensionale e abbiamo una lunghezza di 100 e che $w$ abbia una lunghezza di 5. La lunghezza di output con un passo di 1 o 2 è mostrata nella tabella qui sotto:

1. Padding (“imbottitura”): spesso, nel progettare architetture per reti neurali profonde, vogliamo che l’output di una convoluzione sia della stessa dimensione dell’input. Ciò può essere ottenuto “imbottendo” l’input nelle sue estremità con un certo numero di (usualmente) zeri, usualmente in entrambi i lati. Il padding è usato principalmente per comodità. A volte può impattare le performance e risultare in strani effetti ai bordi; detto ciò, quando si utilizza una nonlinearità del tipo ReLU, il padding con zeri non è una scelta irragionevole.

Reti neurali convoluzionali profonde (DCNN)

Come detto in precedenza, le reti neurali profonde sono normalmente organizzate in ripetizioni alternate di operatori lineari e strati nonlineari a valori puntuali. Nelle reti neurali convoluzionali, l’operatore lineare sarà la convoluzione descritta sopra. C’è anche un terzo tipo di strato, chiamato strato di pooling.

Il motivo per far susseguire più strati di questo tipo è che vogliamo costruire una rappresentazione gerarchica dei dati. Le CNN non devono necessariamente essere limitate al processamento d’immagini, sono anche state applicate con successo a segnali vocali e testi. Tecnicamente possono essere applicate a qualsiasi tipo di dato codificato come vettore, anche se vogliamo che questi vettori rispettino determinate proprietà.

Perché vogliamo catturare una rappresentazione gerarchica del mondo? Perché il mondo in cui viviamo è composizionale. Questo punto era già stato introdotto nelle sezioni precedenti. Una natura gerarchica di questo tipo piò essere intuita dal fatto che i pixel locali si assemblano a formare semplici motivi come bordi orientati. Questi bordi sono a loro volta combinati a formare motivi che sono ancora più astratti. Possiamo continuare a costruire al di sopra di queste rappresentazioni gerarchiche finché arriviamo a formare gli oggetti che osserviamo nel mondo reale.

Fig. 10 Visualizzazione delle caratteristiche di una rete neurale convoluzionale addestrata su ImageNet, da [Zeiler & Fergus 2013]

Questa natura composizionale e gerarchica che osserviamo nel mondo naturale non è quindi solo il risultato della nostra percezione visiva, ma è anche vero in un piano fisico. Al livello più basso della descrizione abbiamo le particelle elementari, che si compongono a formare gli atomi, più atomi formano le molecole, e continuiamo ad accrescere questo processo fino a formare materiali, parti di oggetti e infine oggetti completi nel mondo fisico.

La natura composizionale del mondo potrebbe essere la risposta alla domanda retorica di Einstein riguardo a come gli umani comprendono il mondo in cui vivono:

La cosa più incomprensibile dell’Universo è che esso sia comprensibile.

Il fatto che gli umani comprendano il mondo grazie a questa natura composizionale sembra ancora una specie di cospirazione per Yann. Invece, è dibattuto il fatto che, senza composizionalità, servirebbe qualcosa di ancora più magico agli umani per comprendere il mondo che li circonda. Citando il grande matematico Stuart Geman:

Il mondo è composizionale o Dio esiste.

Ispirazioni dalla biologia

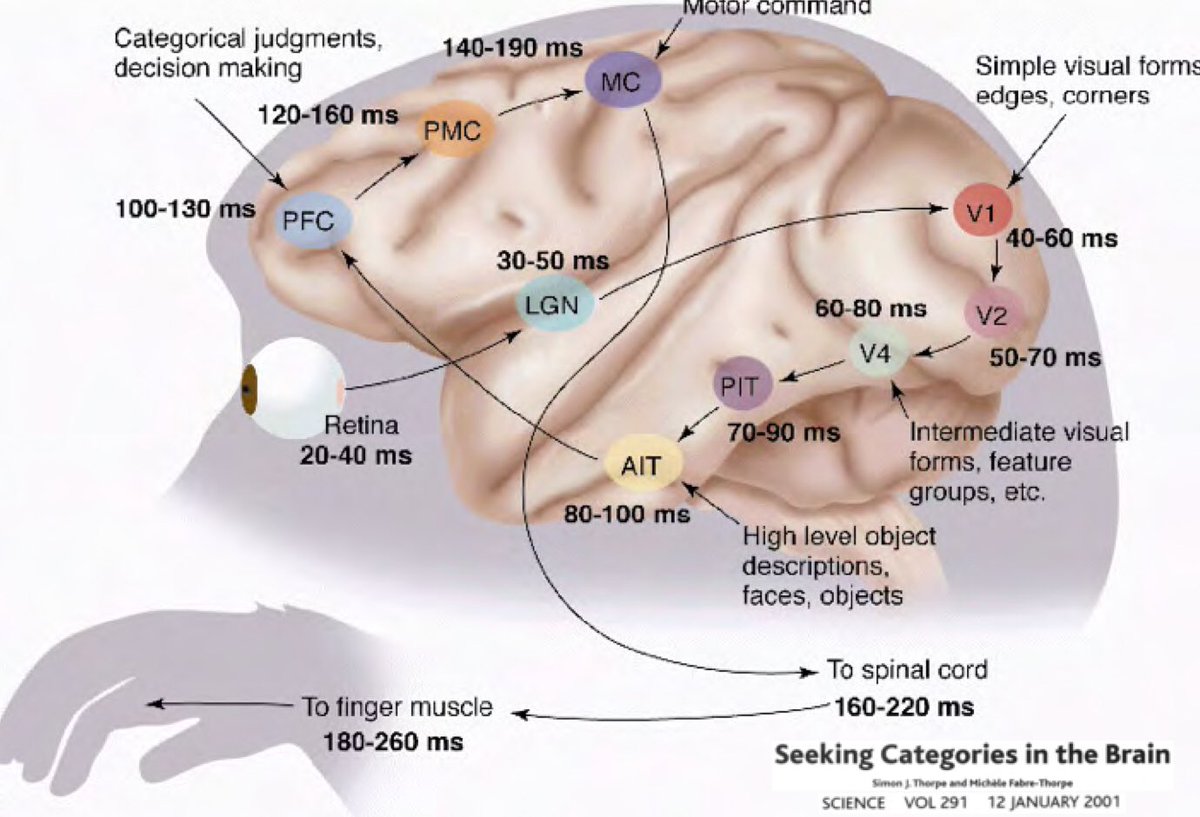
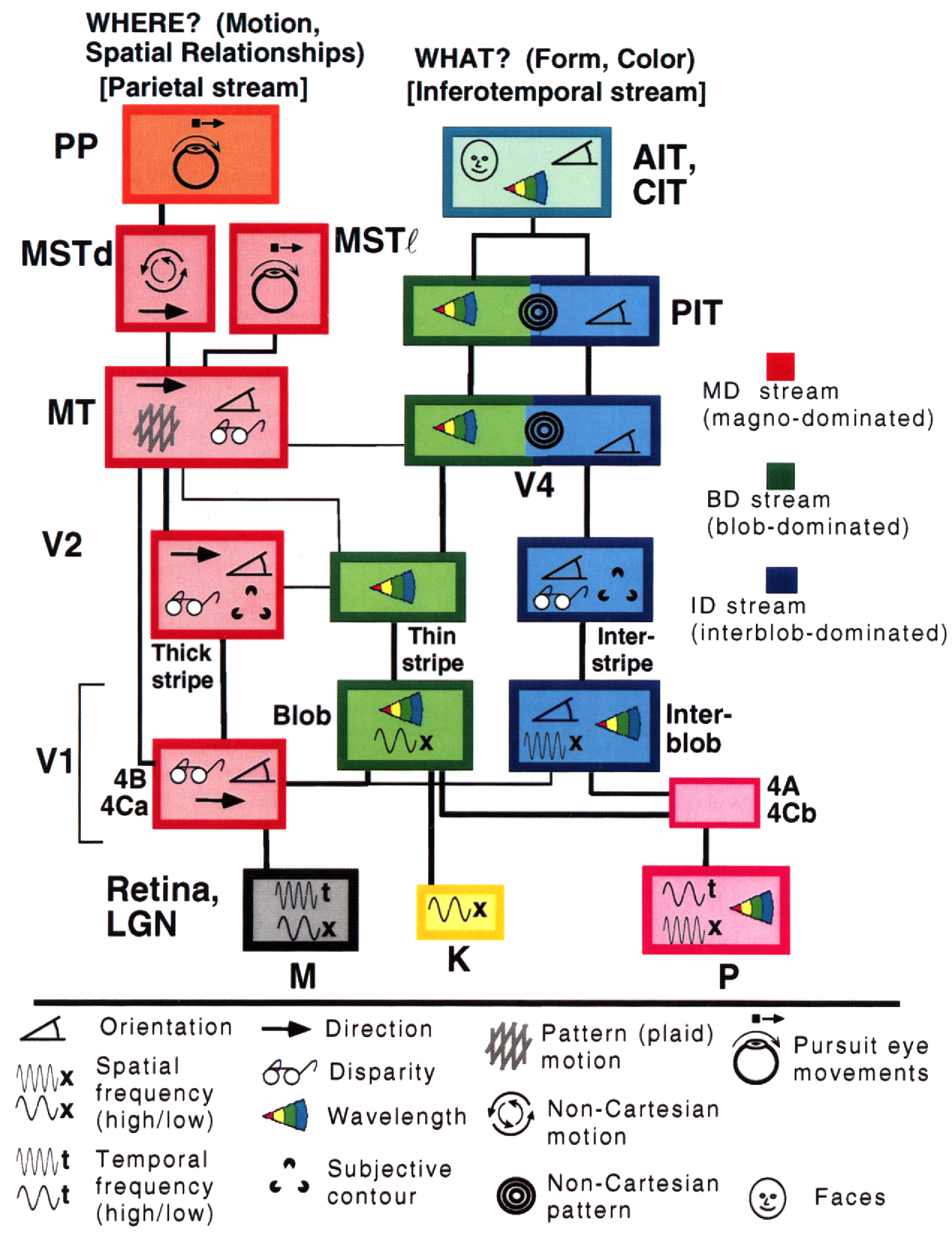
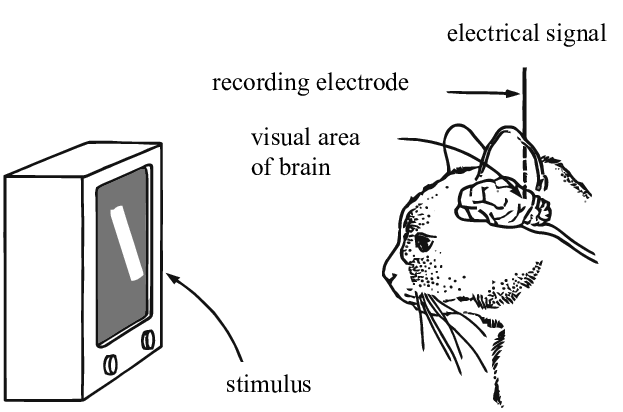
Allora perché l’apprendimento profondo dovrebbe essere basato sull’idea che il nostro mondo sia comprensibile e abbia una natura composizionale? Una ricerca condotta da Simon Thorpe ha permesso di motivare ciò in maniera più ampia. Egli ha mostrato che il modo in cui riconosciamo gli oggetti con cui abbiamo a che fare ogni giorno è estremamente rapido. I suoi esperimenti riguardavano mostrare in rapida successione un insieme di immagini ogni 100ms, per poi chiedere ai partecipanti d’identificare queste immagini, il che erano in grado di fare con successo. Ciò ha dimostrato che gli umani impiegano circa 100ms per riconoscere gli oggetti. Inoltre, si consideri il diagramma qui sotto, illustrante parti del cervello annotate con il tempo che impiegano i neuroni a propagare un segnale da un’area alla successiva.

Fig. 11 Il modello di Simon Thorpe del flusso di informazione visiva nel cervello

</center> I segnali passano dalla retina al LGN (che aiuta al miglioramento del contrasto, teoria del cancello, ecc.), quindi alla corteccia visiva primaria V1, poi V2, V4, quindi alla corteccia inferotemporale (PIT), che è la parte del cervello dove vengono definite le categorie. Delle osservazioni basate su operazioni chirurgiche a cervello aperto hanno elicitato che, se si mostra un film ad un umano, i neuroni nel PIT si attivano solo quando riconoscono certe immagini -- come Jennifer Aniston o la nonna del soggetto -- e null'altro. Le attivazioni neurali sono invarianti a concetti come posizione, dimensione, illuminazione, l'orientamento di tua nonna, che cosa sta indossando, ecc. Inoltre, il rapido tempo di reazione con il quale gli umani erano capaci di categorizzare questi oggetti -- appena sufficiente a far verificare un paio di picchi del segnale -- dimostra che è possibile fare ciò senza dover dedicare tempo ulteriore ad effettuare complessi calcoli ricorrenti; piuttosto, questo è un singolo processo sequenziale. Queste scoperte suggerirono che fosse possibile sviluppare una rete neurale che fosse completamente sequenziale, ma comunque capace di risolvere problemi di riconoscimento rimanendo invariante a trasformazioni dell'input. Una ulteriore intuizione sul cervello umano viene da Gallant & Van Essen, il cui modello del cervello umano illustra due correnti distinte:

Fig. 12 Il modello di Gallen & Van Essen sulle correnti cerebrali dorsale e ventrale

</center> La figura di destra mostra la corrente ventrale, che distingue che cosa si sta guardando, mentre la figura di sinistra mostra la corrente dorsale, che identifica localizzazioni, geometrie e movimenti. Sembrano essere moderatamente separate (con poche interazioni reciproche) nella corteccia visiva umana (e dei primati). ## I contributi di Hubel & Weisel (1962)

Fig. 13 Gli esperimenti di Hubel & Weisel sugli stimoli visivi nel cervello di gatti

</center> Huber e Weisel, nei loro esperimenti, utilizzavano elettrodi per misurare le attivazioni neuronali nel cervello di gatti in risposta a stimoli visivi. Essi scoprirono che i neuroni della regione V1 sono sensibili a determinate aree del campo visivo (chiamate "campi recettivi") e riconoscono i bordi orientati in tale area. Per esempio, hanno dimostrato che, se mostri ad un gatto una riga verticale ed inizi a ruotarla, il neurone si attiverà ad una determinata angolatura della riga. Analogamente, come la riga si discosta da quella determinata angolatura, l'attivazione del neurone si riduce. Huber e Weisel hanno nominato "cellule semplici" questi neuroni selettivi all'attivazione, a causa della loro abilità di riconoscere caratteristiche locali. Inoltre, hanno scoperto che, se scosti la riga al di fuori del campo recettivo, quel particolare neurone non si attiva più, ma lo farà un altro neurone. Ci sono rilevatori di caratteristiche locali corrispondenti a tutte le aree del campo visivo, da cui l'idea che il cervello umano processi le informazioni visive come collezione di "convoluzioni". Un altro tipo di neurone, che Huber e Weisel chiamarono "cellule complesse", aggrega gli output di più "cellule semplici" appartenenti ad una determinata area. Possiamo pensare che queste "cellule complesse" stiano effettuando un'aggregazione delle attivazioni utilizzando a funzioni come il massimo, la somma, la somma di quadrati o qualsiasi altra funzione indipendente dall'ordine dei termini. Esse riconoscono bordi ed orientamenti in una regione, indipendentemente dalla localizzazione specifica degli stimoli all'interno della regione. In altre parole, sono invarianti rispetto a piccole traslazioni della posizione dell'input. ## Contributi di Fukushima (1982)

Fig. 14 Il modello di CNN di Fukushima

</center> Fukushima fu il primo a implementare l'idea di strati multipli di "cellule semplici" e "cellule complesse" in modelli informatici, usando un dataset di cifre scritte a mano. Alcuni di questi rilevatori di caratteristiche erano progettati in maniera artigianale oppure appresi tramite algoritmi di clustering non supervisionato ed addestrati separatamente per ogni strato, in quanto la retropropagazione non era ancora in uso. Yann LeCun arrivò un paio di anni più tardi (1989, 1998) e implementò la stessa architettura, questa volta addestrata in un setting supervisionato e utilizzando la retropropagazione. Questa è ampiamente considerata la genesi delle reti neurali convoluzionali moderne. (Nota: Riesenhuber all'MIT nel 1999 ri-scoprì pure lui queste architetture, ma non utilizzò la retropropagazione).