Reti Neurali Artificiali (ANNs)

🎙️ Alfredo Canziani

Apprendimento supervisionato per la classificazione

• Si consideri la Fig. 1(a) sotto. I punti in questo grafico si trovano sui rami della spirale, e vivono in $\R^2$. Ogni colore rappresenta una classe. Il numero di classi univoche è $K = 3$. Questo è rappresentato matematicamente dalla Eqz. 1(a).

• La Fig. 1(b) Mostra una spirale simile, con aggiunto del rumore gaussiano. Questo è rappresentato matematicamente da Eqz. 1(b).

  In entrambi i casi i punti non sono linearmente separabili.

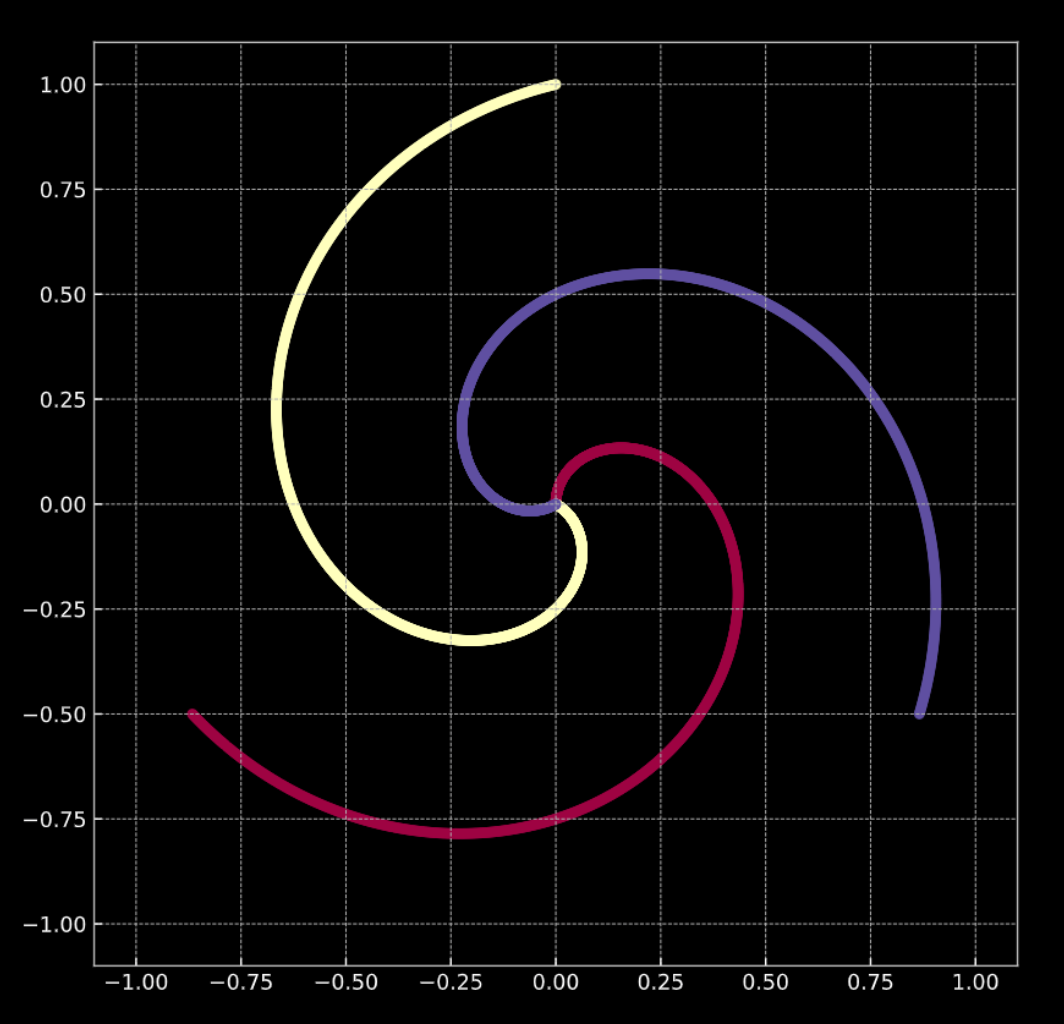
  Fig. 1(a) spirale 2D "pulita"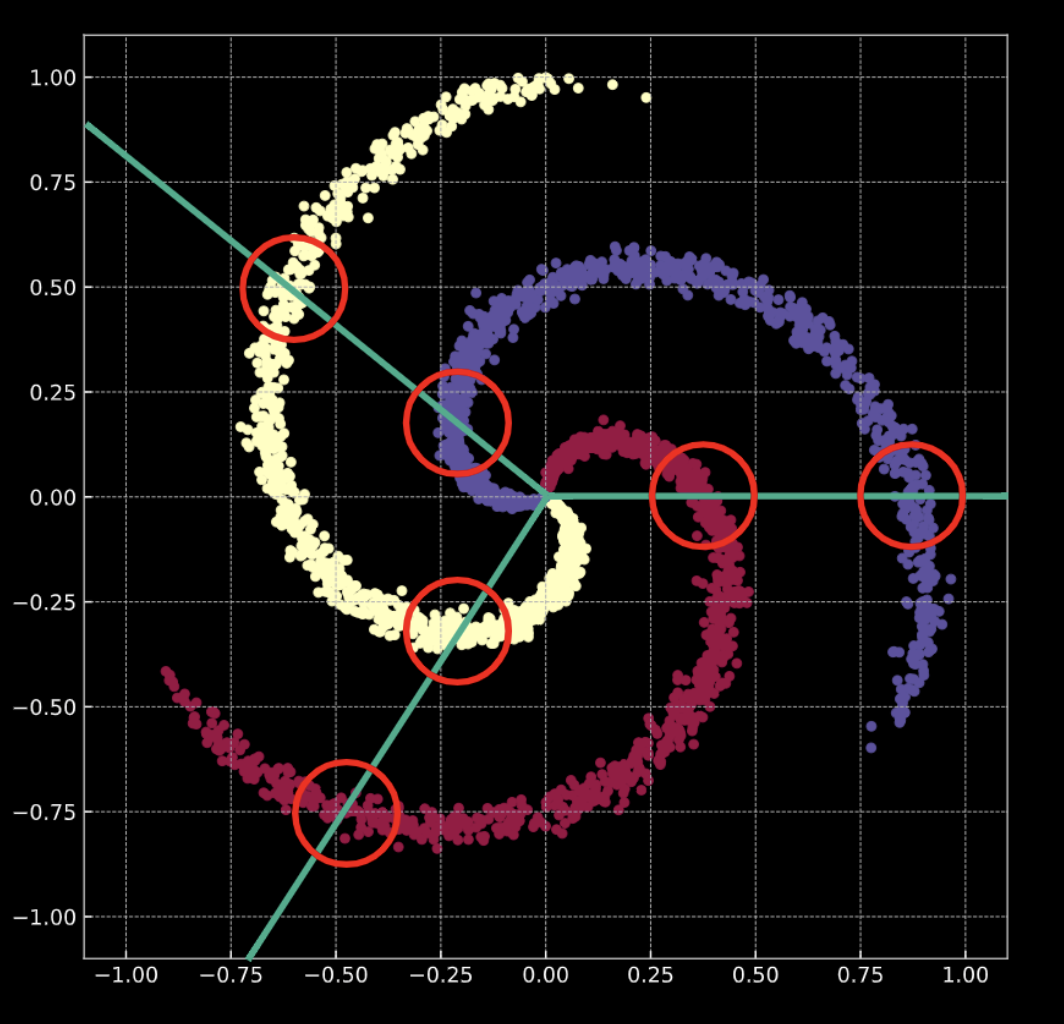

  Fig. 1(b) spirale 2D con rumore aggiunto

\[X_{k}(t)=t\left(\begin{array}{c}{\sin \left[\frac{2 \pi}{K}(2 t+k-1)\right]} \\ {\cos \left[\frac{2 \pi}{K}(2 t+k-1)\right]}\end{array}\right) \\ 0 \leq t \leq 1, \quad k=1, ..., K\] Eqz. 1(a) \[X_{k}(t)=t\left(\begin{array}{c}{\sin \left[\frac{2 \pi}{K}(2 t+k-1 +\mathcal{N}\left(0, \sigma^{2}\right))\right]} \\ {\cos \left[\frac{2 \pi}{K}(2 t+k-1 +\mathcal{N}\left(0, \sigma^{2}\right))\right]}\end{array}\right)\\0 \leq t \leq 1, \quad k=1, ..., K\] Eqz. 1(b)

Cosa vuol dire eseguire una classificazione? Si consideri il caso della regressione logistica. Se applicassimo la regressione logistica per classificare questi dati, creerebbe un insieme di piani lineari (identificanti i cd. “confini delle decisioni”, in inglese decision boundaries) nel tentativo di separare i dati nelle classi di loro appartenenza. Il problema di questa soluzione è che in ogni regione ci sono punti che appartengono a diverse classi. I rami della spirale incrociano i confini lineari. Questa non è una buona soluzione!

Come sistemiamo ciò? Trasformiamo lo spazio d’input in modo che i dati siano forzati a essere linearmente separabili. Nel corso dell’addestramento della rete neurale, per fare ciò, i confini delle decisioni imparati dal modello proveranno ad adattarsi alla distribuzione dei dati d’addestramento.

Nota: Una rete neurale è sempre rappresentata dal basso all’alto. Il primo strato è in basso, e l’ultimo è in alto. QUesto perché concettualmente i dati in input sono caratteristiche a basso livello per qualsiasi compito che vuole svolgere la rete neurale. Come i dati attraversano verso l’alto la rete ogni strato successivo estrae caratteristiche di livello più alto.

Dati d’addestramento

La scorsa settimana, abbiamo visto che una rete neurale appena inizializzata trasforma il suo input in modo arbitrario. Questa trasformazione, tuttavia, non è (inizialmente) di valido aiuto nel risolvere il compito d’interesse. Esploriamo come, usando i dati, possiamo forzare la trasformazione ad avere qualche informazione rilevante per il compito da svolgere. I dati seguenti sono utilizzati per l’addestramento di una rete.

• $\vect{X}$ rappresenta i dati in input, una matrice di dimensione $m$ (numero dei dati d’addestramento) x $n$ (dimensione di ogni punto in input). Nel caso dei dati delle figure 1(a) e 1(b), $n = 2$.

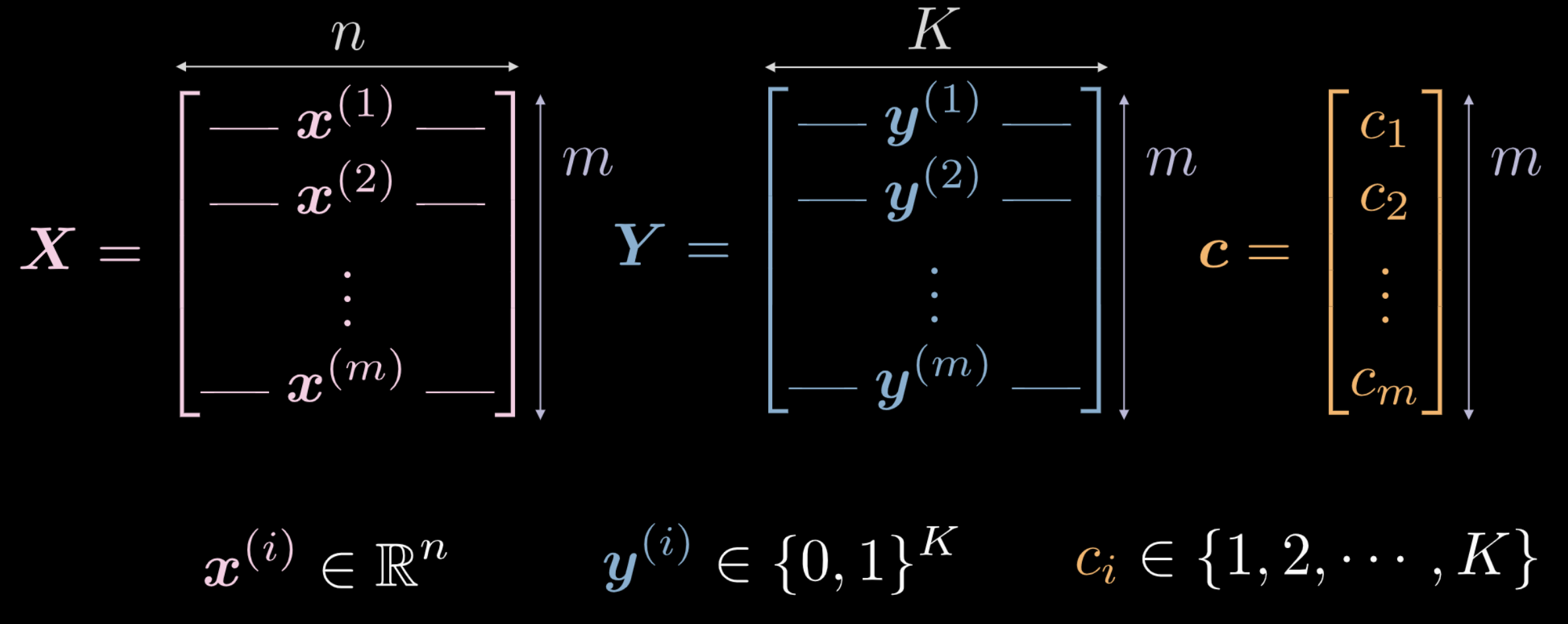
Fig. 2 Dati d'addestramento

• Il vettore $\vect{c}$ e la matrice $\boldsymbol{Y}$ rappresentano entrambe le etichette delle classi per ognuno dei punti $m$. Nell’esempio sopra ci sono $3$ classi distinte.

  • $c_i \in \lbrace 1, 2, \cdots, K \rbrace$ e $\vect{c} \in \R^m$. Tuttavia, potremmo non usare $\vect{c}$ come dati d’addestramento. Se usiamo etichette per le classi numeriche $c_i \in \lbrace 1, 2, \cdots, K \rbrace$, la rete potrebbe dedurre un ordine delle classi che non è rappresentativo della distribuzione dei dati.
  • Per aggirare questo problema, usiamo un vettore di componenti binarie (one-hot encoding). Per ogni etichetta $c_i$, un vettore di zeri $K$ dimensionale $\vect{y}^{(i)}$ viene creato, ma con il $c_i$-esimo elemento settato a $1$ (guarda Fig. 3 sotto).

Fig. 3 vettore di componenti binarie (*one-hot encoding*)

• Tuttavia, $\boldsymbol Y \in \R^{m \times K}$. Questa matrice può essere pensata come se avesse una sorta di massa probabilistica, che è totalmente concentrata in uno dei $K$ punti.

Strati completamente (densamente) connessi (Fully-Connected (_FC_) layers)

Ora daremo un’occhiata a una rete completamente connessa (FC) e a come funziona.

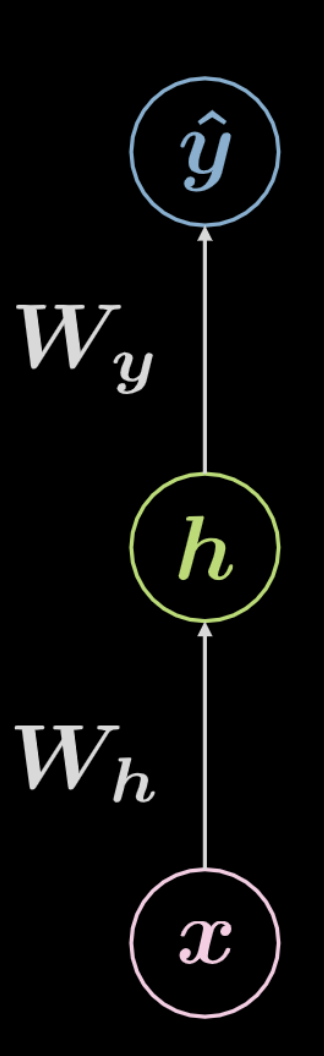
Fig. 4 Rete completamente connessa

Si consideri la rete mostrata sopra nella Fig. 4. Il dato in input, $\boldsymbol x$, è soggetto a una trasformazione affine definita da $\boldsymbol W_h$, seguita da una trasformazione non-lineare. Il risultato di questa trasformazione non-lineare è denotato da $\boldsymbol h$, rappresentante un output nascosto , ovvero, uno strato il cui output non è visto dall’esterno della rete. Questo è seguito da un’altra trasformazione affine ($\boldsymbol W_y), seguita da un’altra trasformazione non-lineare. Questo produce l’output finale $\boldsymbol{\hat{y}}$. Questa rete può essere rappresentata matematicamente dalle equazioni in Eqn. 2 sotto. \(f\) e \(g\) are sono entrambi non lineari.

\[\begin{aligned} &\boldsymbol h=f\left(\boldsymbol{W}_{h} \boldsymbol x+ \boldsymbol b_{h}\right)\\ &\boldsymbol{\hat{y}}=g\left(\boldsymbol{W}_{y} \boldsymbol h+ \boldsymbol b_{y}\right) \end{aligned}\] Eqn. 2 Matematica dietro una rete FC

Una rete neurale basilare come quella mostrata sopra è semplicemente un insieme di coppie successive, con ogni coppia che è una trasformazione affine seguita da una operazione non lineare (“schiacciamento”, squashing). Le funzioni non-lineari usate di frequente sono ReLU, sigmoidale (Sigmoid), tangente iperbolica e SoftMax.

La rete mostrata sopra è una rete a 3 strati:

1. neuroni di input
2. neuroni di nascosto
3. neuroni di output

Di conseguenza, una rete neurale a $3$ strati ha $2$ trasformazioni affini. Questo può esse esteso ad una rete a $n$ strati.

Ora spostiamoci su un caso più complicato.

Consideriamo un caso con 3 strati nascosti, completamente connesso in ogni strato. Un’illustrazione può essere visualizzata nella Fig. 5

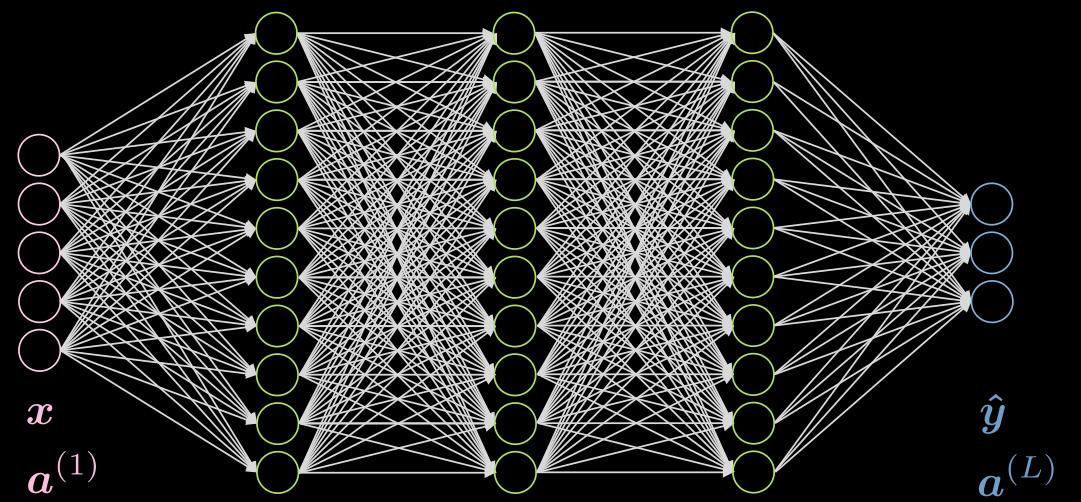
Fig. 5 Rete neurale con 3 strati nascosti.

Si consideri il neruone $j$ nel secondo strato. La sua funzione d’attivazione è:

\[a^{(2)}_j = f(\boldsymbol w^{(j)} \boldsymbol x + b_j) = f\Big( \big(\sum_{i=1}^n w_i^{(j)} x_i\big) +b_j ) \Big)\]

Dove $\vect{w}^{(j)}$ è la $j$-esima riga di $\vect{W}^{(1)}$.

Si noti che l’attivazione dello strato di input in questo caso è l’identità. Gli strati nascosti possono avere funzioni d’attivazione come ReLU, sigmoidale (Sigmoid), tangente iperbolica e Soft/ArgMax, ecc.

L’attivazione dell’ultimo strato in generale dipende dal caso d’uso, come spiegato in questo post di Piazza.

Rete neurale (inferenza)

Ripensiamo ancora alla rete a 3 strati (input, nascosto, output), come si vede nella Fig. 6.

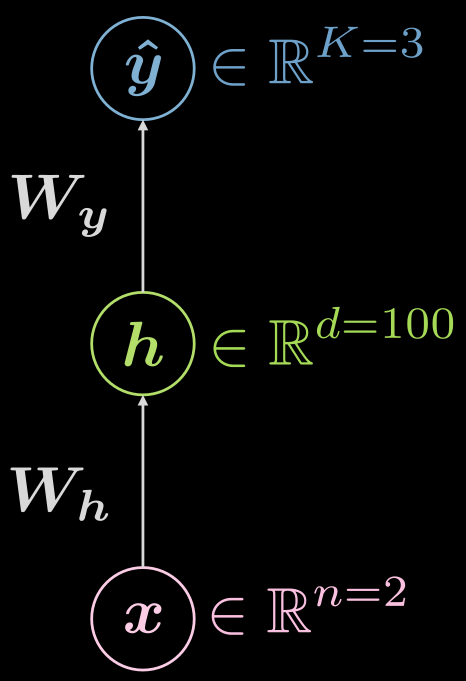
Fig. 6 Rete neurale a tre strati

A che tipo di funzioni stiamo guardando?

\[\boldsymbol {\hat{y}} = \boldsymbol{\hat{y}(x)}, \boldsymbol{\hat{y}}: \mathbb{R}^n \rightarrow \mathbb{R}^K, \boldsymbol{x} \mapsto \boldsymbol{\hat{y}}\]

Tuttavia, è utile visualizzare che c’è uno strato nascosto, e la mappatura può essere espansa come:

\[\boldsymbol{\hat{y}}: \mathbb{R}^{n} \rightarrow \mathbb{R}^d \rightarrow \mathbb{R}^K, d \gg n, K\]

Come dovrebbe apparire una configurazione di esempio per i casi sopra? In questo caso, si ha dimensione di input due ($n=2$), il singolo strato nascosto potrebbe avere dimensione di 1000 ($d = 1000$), e abbiamo 3 classi ($C=3$). Ci sono buone ragioni pratiche per non avere così tanti neuroni in uno strato nascosto: avrebbe così senso divire il singolo strato nascosto in 3 parti con 10 neuroni ciascuno ($1000 \rightarrow 10 \times 10 \times 10$).

Rete neurale (addestramento I)

Come dovrebbe prefigurarsi il tipico addestramento? È utile formulare questa domanda nella terminologia standard della funzione di perdita.

Prima, reintroduciamo la funzione di Soft/ArgMax che esplicitiamo essere una funzione d’attivazione comune per l’ultimo strato, quando si usa una perdita come la log-verosimiglianza negativa, nei casi di previsione multi-classe. Come constatato dal Professor LeCun nella lezione, questo perché si ottengono gradienti migliori rispetto all’utilizzo di una funzione di attivazione sigmoidale o alla funzione di perdita quadratica (square loss). In aggiunta, l’ultimo strato sarà già normalizzato (la somma di tutti i neuroni nell’ultimo layer è 1), in una maniera migliore per i metodi a gradiente rispetto alla normalizzazione esplicita (divisione per la norma).

La funzione Soft/ArgMax produrrà dei logit (logaritmi dei rapporti di scommessa) nell’ultimo strato che assomiglieranno a ciò:

\[\text{soft{(arg)}max}(\boldsymbol{l})[c] = \frac{ \exp(\boldsymbol{l}[c])} {\sum^K_{k=1} \exp(\boldsymbol{l}[k])} \in (0, 1)\]

È importante notare che l’insieme non è chiuso perché la funzione esponenziale è strettamente positiva per natura.

Dato un insieme di predizioni $\matr{\hat{Y}}$, la perdita sarà:

\[\mathcal{L}(\boldsymbol{\hat{Y}}, \boldsymbol{c}) = \frac{1}{m} \sum_{i=1}^m \ell(\boldsymbol{\hat{y}_i}, c_i), \quad \ell(\boldsymbol{\hat{y}}, c) = -\log(\boldsymbol{\hat{y}}[c])\]

Qui $c$ denota l’etichetta nella sua specificazione naturale, non la rappresentazione della codifica one-hot.

Facciamo due esempi, uno dove l’esempio è correttamente classificato, e uno dove non lo è.

Poniamo

\[\boldsymbol{x}, c = 1 \Rightarrow \boldsymbol{y} = {\footnotesize\begin{pmatrix} 1 \\ 0 \\ 0 \end{pmatrix}}\]

Qual è la perdita a livello d’istanza?

Per il caso di una quasi perfetta previsione ($\sim$ sta a significare circa):

\[\hat{\boldsymbol{y}}(\boldsymbol{x}) = {\footnotesize\begin{pmatrix} \sim 1 \\ \sim 0 \\ \sim 0 \end{pmatrix}} \Rightarrow \ell \left( {\footnotesize\begin{pmatrix} \sim 1 \\ \sim 0 \\ \sim 0 \end{pmatrix}} , 1\right) \rightarrow 0^{+}\]

Per il caso di una previsione quasi completamente errata:

\[\hat{\boldsymbol{y}}(\boldsymbol{x}) = {\footnotesize\begin{pmatrix} \sim 0 \\ \sim 1 \\ \sim 0 \end{pmatrix}} \Rightarrow \ell \left( {\footnotesize\begin{pmatrix} \sim 0 \\ \sim 1 \\ \sim 0 \end{pmatrix}} , 1\right) \rightarrow +\infty\]

Si noti che negli esempi sopra, $\sim 0 \rightarrow 0^{+}$ e $\sim 1 \rightarrow 1^{-}$. Perché questo? Si prendano un minuto per pensarci.

Nota: è importante sapere che se si usa CrossEntropyLoss (perdita a entropia incrociata), si avrà LogSoftMax e una NLLLoss (perdita a log-verosimiglianza negativa) uniti insieme, quindi si eviti di farlo due volte!

Rete neurale (addestramento II)

Per l’addestramento, aggreghiamo tutti i parametri addestrabili – matrici dei pesi e bias – in una collezione che chiamiamo $\mathbf{\Theta} = \lbrace\boldsymbol{W_h, b_h, W_y, b_y} \rbrace$. Questo ci permette di scrivere la funzione obiettivo o di perdita come:

\[J \left( \mathbf{\Theta} \right) = \mathcal{L} \left( \boldsymbol{\hat{Y}} \left( \mathbf{\Theta} \right), \boldsymbol c \right) \in \mathbb{R}^{+}\]

Questo fa sì che la funzione di perdita dipenda dall’output della rete $\boldsymbol {\hat{Y}} \left( \mathbf{\Theta} \right)$, cosicché possiamo trasformarlo in un problema di ottimizzazione.

Una semplice illustrazione di come ciò funzioni può essere vista nella Fig. 7, dove $J(\vartheta)$, la funzione che dobbiamo minimizzare, ha solo un parametro scalare $\vartheta$.

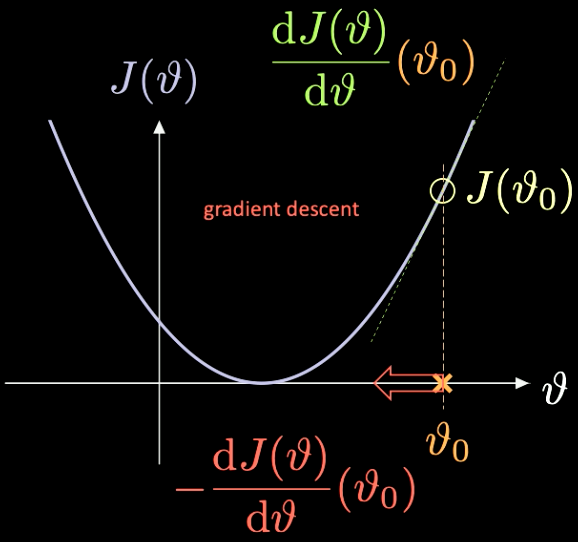
Fig. 7 Ottimizzazione di una funzione attraverso la discesa del gradiente.

Prendiamo un punto d’inizializzazione casuale $\vartheta_0$ – con associata una funzione di perdita $J(\vartheta_0)$. Possiamo calcolare la derivata calcolata nel punto $J’(\vartheta_0) = \frac{\text{d} J(\vartheta)}{\text{d} \vartheta} (\vartheta_0)$. In questo caso, la pendenza della derivata è positiva. Quindi dobbiamo fare un passo nella direzione del gradiente discendente più ripido. In questo caso è $-\frac{\text{d} J(\vartheta)}{\text{d} \vartheta}(\vartheta_0)$.

La ripetizione iterativa di questo processo è conosciuta come discesa del gradiente. I metodi a gradiente sono gli strumenti principali per addestrare una rete neurale.

Per poter calcolare i gradienti necessari, dobbiamo utilizzare la retropropagazione

\[\frac{\partial \, J(\mathbf{\Theta})}{\partial \, \boldsymbol{W_y}} = \frac{\partial \, J(\mathbf{\Theta})}{\partial \, \boldsymbol{\hat{y}}} \; \frac{\partial \, \boldsymbol{\hat{y}}}{\partial \, \boldsymbol{W_y}} \quad \quad \quad \frac{\partial \, J(\mathbf{\Theta})}{\partial \, \boldsymbol{W_h}} = \frac{\partial \, J(\mathbf{\Theta})}{\partial \, \boldsymbol{\hat{y}}} \; \frac{\partial \, \boldsymbol{\hat{y}}}{\partial \, \boldsymbol h} \;\frac{\partial \, \boldsymbol h}{\partial \, \boldsymbol{W_h}}\]

Classificazione nella spirale - Jupyter notebook

Il Jupyter notebook può essere trovato qui. Per lanciare il notebook, assicurati di aver l’ambiente the dl-minicourse installato come specificato in README.md.

La spiegazione su come usare torch.device() può essere trovata negli appunti dell’ultima settimana.

Come prima, andremo a lavorare coi punti in $\mathbb{R}^2$ con tre diverse etichette delle categorie – rosso, giallo e blu – come si può vedere nella Fig. 8.

Fig. 8 Classificazione dei dati nella configurazione a spirale.

nn.Sequential() è un contenitore, che passa i moduli al costruttore nell’ordine in sono ad esso aggiunti; nn.linear() non è nominato correttamente perché applica una trasformazione affine ai dati che gli vengono passati: $\boldsymbol y = \boldsymbol W \boldsymbol x + \boldsymbol b$. Per maggiori informazioni si veda PyTorch documentation.

Si ricordi, una trasformazione affine può essere cinque cose: rotazione, riflessione, traslazione, ridimensionamento (scaling) e taglio (shearing)

Come si può vedere nella Fig. 9, provando a separare i dati della spirale con confini lineari - usando solo i moduli nn.linear(), senza non-linearità tra loro - il miglior risultato che possiamo avere è un’accuratezza del $50\%$.

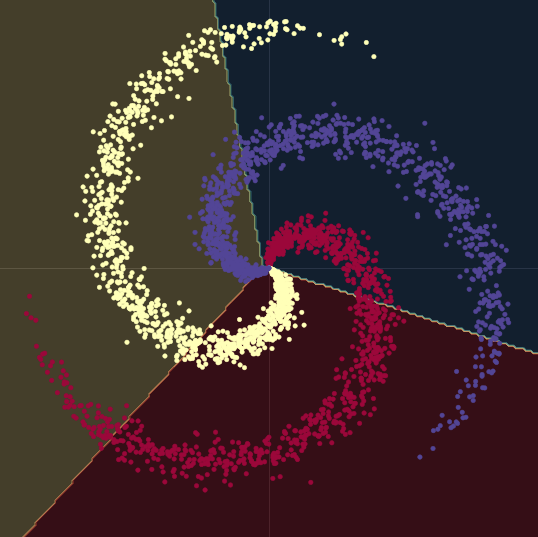
Fig. 9 Confini di decisione lineari (*linear decision boundaries*).

Quando andiamo da un modello lineare a uno con due moduli nn.linear() e un nn.ReLU() tra loro, l’accuratezza arriva fino al $95\%$. Questo perché i confini diventano non lineari e si adattano molto meglio alla forma della spirale formata dai dati, come si può vedere nella Fig. 10.

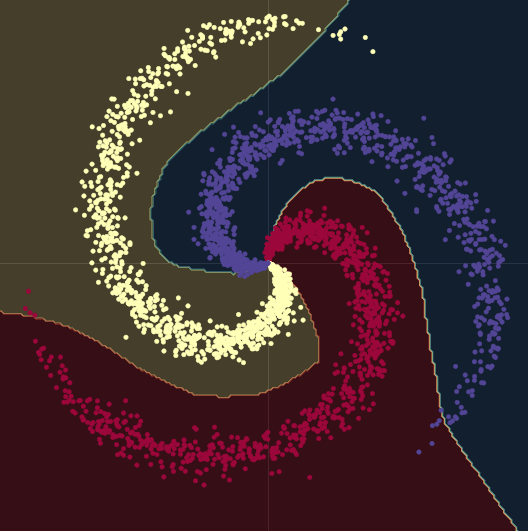
Fig. 10 Confini decisionali non lineari.

Un esempio di un problema di regressione che non può essere risolto correttamente con una regressione lineare, ma può anche essere risolto facilmente con la stessa struttura della rete può essere visto in questo notebook e in Fig. 11, che mostra 10 diverse reti, dove 5 hanno una funzione di attivazione nn.ReLU() e 5 hanno una nn.Tanh(). Il primo è una funzione lineare a tratti, mentre la seconda è una regressione continua e liscia.

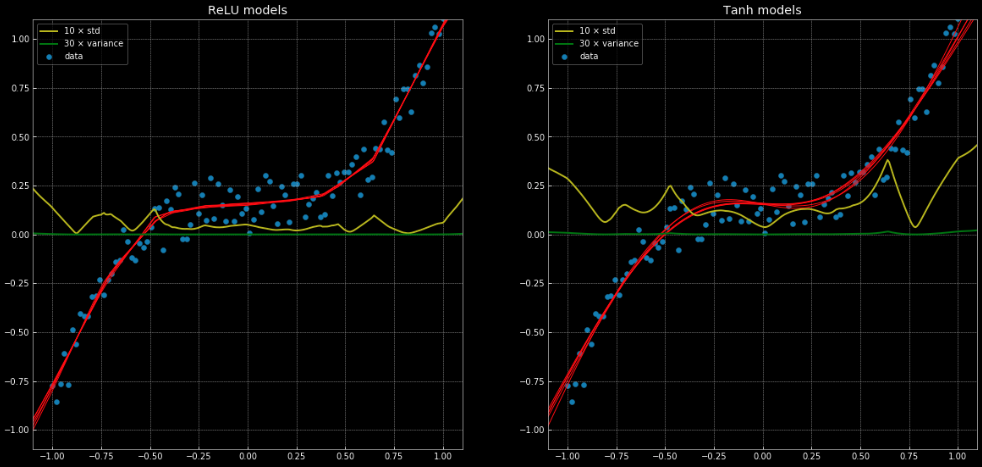
Fig. 11: 10 Reti neurali, con la loro varianza e deviazione standard.
Sinistra: Cinque reti ReLU. Destra: Cinque reti tanh.

Le linee gialle e verdi mostrano la deviazione standard e la varianza per le reti. Il loro utilizzo è utile per qualcosa di simile a un “intervallo di confidenza” – dato che le funzioni danno una singola previsione per output. Il raggruppamento delle previsioni ad ottenere la varianza ci permette di stimare l’incertezza con cui la previsione viene formulata. L’importanza di questo può essere visto nella Fig. 12, dove abbiamo esteso le funzione di decisione al di fuori dell’intervallo di addestramento e queste tendono verso $+\infty, -\infty$.

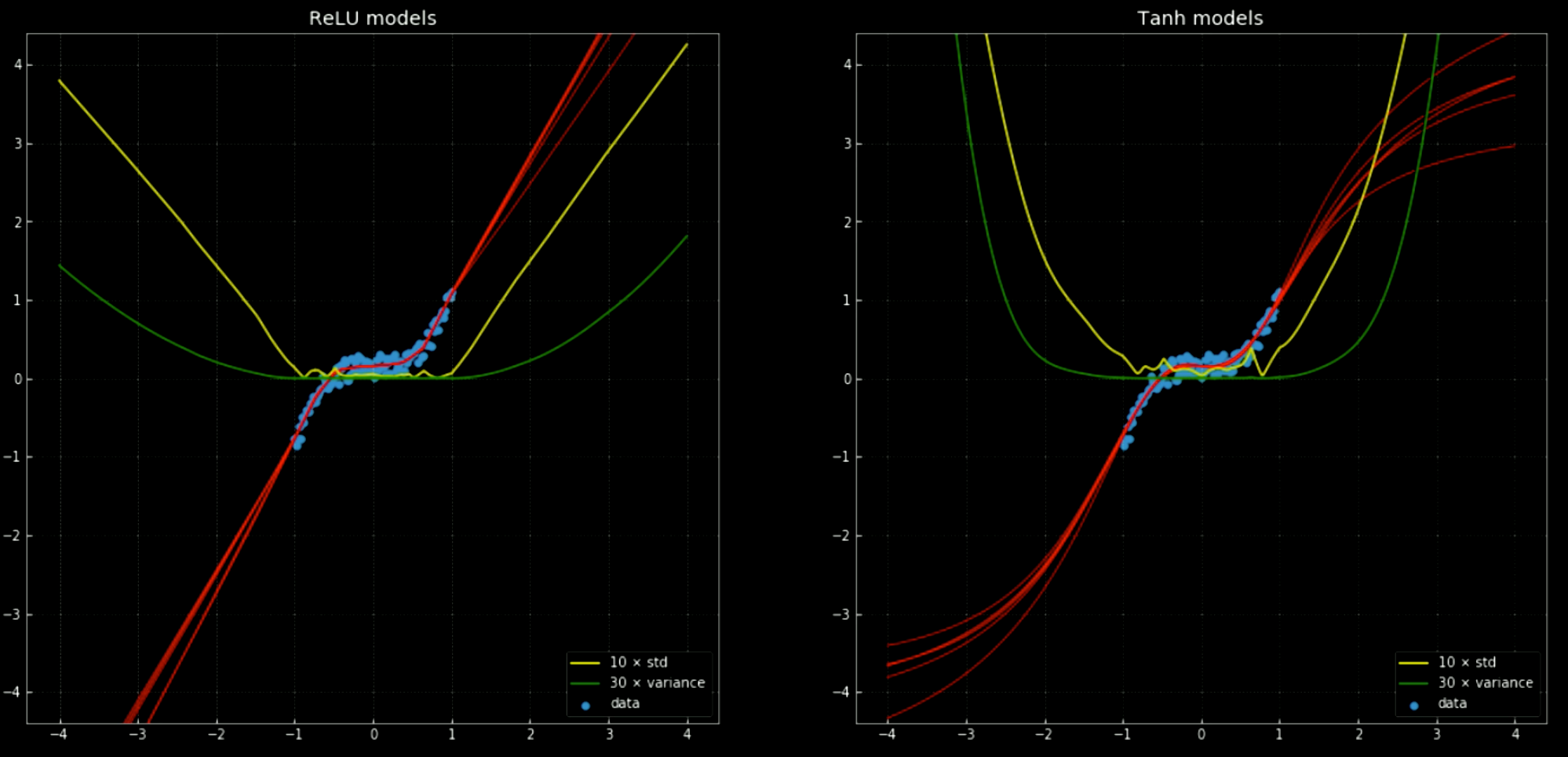
Fig. 12 Rete neurale, con media e deviazione standard, fuori dall'intervallo di addestramento.
Sinistra: Cinque reti ReLU. Destra: Cinque reti tanh.

Per addestrare ogni Rete Neurale usando PyTorch, si necessitano 5 stadi fondamentali nel ciclo di addestramento:

1. output = model(input) è il passo in avanti (forward pass) del modello, che prende l’input e genera l’output.
2. J = loss(output, target <or> label) prende l’output del modello e calcola la perdita dell’addestramento rispetto all’obiettivo o classe reale di appartenenza del dato.
3. model.zero_grad() pulisce i calcoli del gradiente, cosicché non saranno accumulati al passo successivo.
4. J.backward() effettua una retropropagazione e accumulazione: Calcola $\nabla_\texttt{x} J$ per ogni variabile $\texttt{x}$ per la quale è specificato requires_grad=True. Questi sono accumulati nel gradiente di ogni variabile: $\texttt{x.grad} \gets \texttt{x.grad} + \nabla_\texttt{x} J$.
5. optimiser.step() effettua un passo nella direzione di discesa del gradiente: $\vartheta \gets \vartheta - \eta\, \nabla_\vartheta J$.

Quando si addestra una NN, è molto probabile si necessiterà di questi cinque passi nell’ordine in cui sono stati presentati.

---

Yuri Gardinazzi
4 Feb 2020