Calcolo dei gradienti per i moduli delle reti neurali e accorgimenti pratici per la retropropagazione

Esempio concreto di retropropagazione e introduzione ai moduli basilari di reti neurali

Esempio

Considereremo di seguito un esempio concreto di retropropagazione (backpropagation) accompagnato da una visualizzazione. La funzione arbitraria $G(w)$ è l’input della funzione di costo $C$, che può essere rappresentata da un grafo. Attraverso la manipolazione della moltiplicazione delle matrici Jacobiane, possiamo trasformare questo grafo in un altro grafo che calcolerà i gradienti muovendosi all’indietro. (Si noti che Pytorch e TensorFLow fanno questo in automatico per l’utente, ovvero, il grafo in avanti è automaticamente “invertito” per creare il grafo delle derivate che retropropaga il gradiente.)

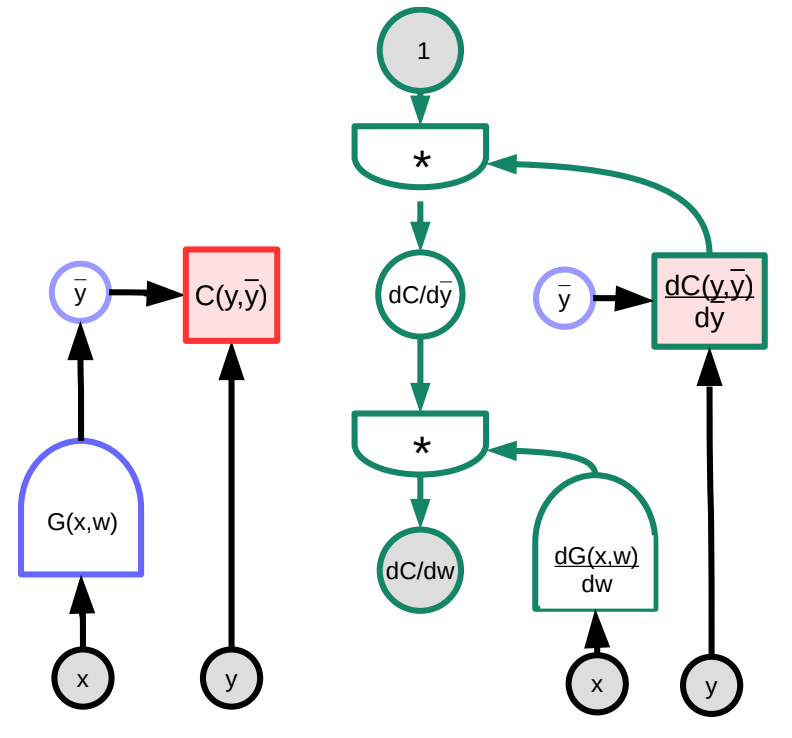
In questo esempio, il grafo verde sulla destra rappresenta il grafo del gradiente. Seguendo il grafo dal suo nodo più alto, segue che

In termini di dimensioni, $\frac{\partial C(y,\bar{y})}{\partial w}$ è un vettore di riga di dimensione $1\times N$ dove $N$ è il numero di componenti di $w$; $\frac{\partial C(y,\bar{y})}{\partial \bar{y}}$ è un vettore riga di dimensione $1\times M$, dove $M$ è la dimensione dell’output; $\frac{\partial \bar{y}}{\partial w}=\frac{\partial G(x,w)}{\partial w}$ è una matrice $M\times N$, dove $M$ è il numero di output di $G$ e $N$ è la dimensione di $w$.

Si noti che potrebbero sorgere delle complicazioni quando l’architettura del grafo non è fissa, ma dipende dai dati. Per esempio, potremmo fissare un modulo di una rete neurale che dipende dalla lunghezza del vettore in input. Anche se questo è possibile, diventa di difficoltà sempre superiore gestire questa variazione quando il numero dei cicli da computare eccede una quantità ragionevole.

Moduli base di reti neurali

Esistono diversi dipi di moduli pre-costruiti oltre ai familiari moduli Linear e ReLU. Questi sono utili perché sono ottimizzati individualmente per eseguire le loro rispettive funzioni (invece di essere costruiti da una combinazione di altri moduli elementari)

• Linear: $Y=W\cdot X$

  \[\begin{aligned} \frac{dC}{dX} &= W^\top \cdot \frac{dC}{dY} \\ \frac{dC}{dW} &= \frac{dC}{dY} \cdot X^\top \end{aligned}\]

• ReLU: $y=(x)^+$

  \[\frac{dC}{dX} = \begin{cases} 0 & x<0\\ \frac{dC}{dY} & \text{altrimenti} \end{cases}\]

• Duplicate (Duplica): $Y_1=X$, $Y_2=X$

  • Simile a “Y - splitter” dove entrambi gli output sono uguali all’input.

  • Quando si retropropaga, i gradienti sono sommati

  • Può essere diviso in $n$ rami in maniera analoga

    \[\frac{dC}{dX}=\frac{dC}{dY_1}+\frac{dC}{dY_2}\]

• Add (Somma): $Y=X_1+X_2$

  • Con due variabili sommate, quando una è perturpbta, l’output sarà perturbato dalla stessa quantità, ovvero,

    \[\frac{dC}{dX_1}=\frac{dC}{dY}\cdot1 \quad \text{e}\quad \frac{dC}{dX_2}=\frac{dC}{dY}\cdot1\]

• Max: $Y=\max(X_1,X_2)$

  • Dal momento che questa funzione può essere rappresentata come
  \[Y=\max(X_1,X_2)=\begin{cases} X_1 & \text{se } X_1 > X_2 \\ X_2 & \text{altrimenti} \end{cases} \Rightarrow \frac{dY}{dX_1}=\begin{cases} 1 & \text{se } X_1 > X_2 \\ 0 & \text{altrimenti} \end{cases}\]

  • Perciò, per derivata della composta,

    \[\frac{dC}{dX_1}=\begin{cases} \frac{dC}{dY}\cdot1 & \text{se } X_1 > X_2 \\ 0 & \text{altrimenti} \end{cases}\]

LogSoftMax vs SoftMax

La funzione SoftMax, che è anche un modulo Pytorch, è un modo conveniente di trasformare un gruppo di numeri reali in un gruppo di numeri positivi tra $0$ e $1$ che sommano a uno. Questi numeri possono essere interpretati come una distribuzione di probabilità. Di conseguenza, è comunemente utilizzata nei problemi di classificazione. $y_i$ nell’equazione sotto è un vettore di probabilità per tutte le categorie.

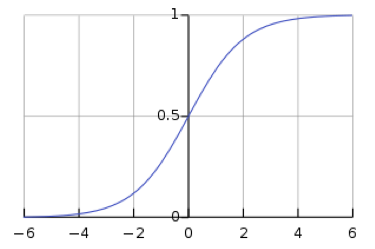
Tuttavia, l’uso di SoftMax rende la rete suscettibile alla scomparsa del gradiente (vanishing gradients, talvolta tradotto anche come “gradiente/i evanescente/i”). La scomparsa del grediente è un problema: impedisce ai pesi a valle di essere modificati dalla rete neurale, il che potrebbe impedire completamente da un ulteriore addestramento. La funzione logistica sigmoidale (sigmoid, anche indicata solamente come “sigmoidale”), che è la funzione SoftMax per un singolo valore, mostra che quando $s$ è grande, $h(s)$ è $1$, e quando s è piccolo, $h(s)$ è $0$. Perché la funzione sigmoidale è piatta in $h(s) = 0$ e $h(s) = 1$, il gradiente è $0$, il che risulta nella scomparsa del gradiente.

I matematici hanno pensato all’idea della LogSoftMax per risolvere il problema della scomparsa del gradiente causata dalla SoftMax. LogSoftMax è un altro modulo base in PyTorch. Come si può vedere nell’equazione sotto, LogSoftMax è una combinazione di SoftMax e la il logaritmo naturale.

L’equazione sotto mostra un altro modo di vedere la stessa equazione. La figura sotto visualizza la parte della funzione corrispondente a $\log(1 + \exp(s))$. Quando $s$ è molto piccolo, il valore è $0$, e quando $s$ è molto grande, il valore è $s$. Grazie a ciò non satura e risolve il problema della scomparsa del gradiente.

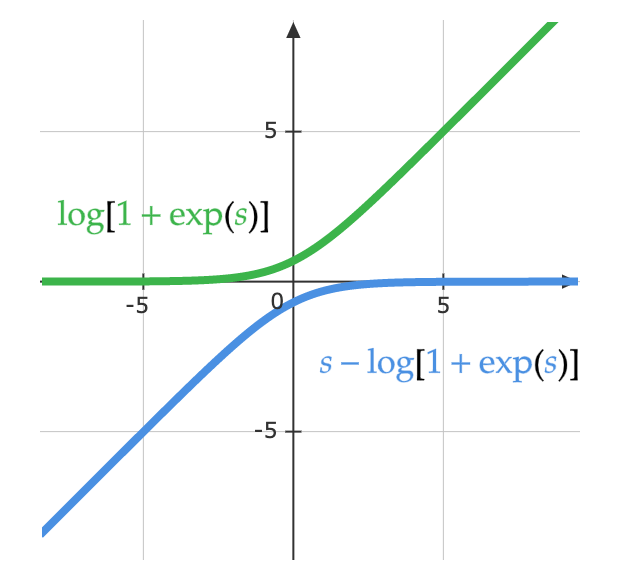
Accorgimenti pratici per la retropropagazione

Usare ReLU come funzione d’attivazione non-lineare

La ReLU funziona al meglio nelle reti con molti strati, il che ha causato un generale calo dell’utilizzo delle alternative come la funzione sigmoidale e la tangente iperbolica $\tanh(\cdot)$. La ragione per cui la ReLU funziona meglio è dovuta alla singola peculiarità, ovvero l’equivarianza alla riscalatura.

Uso ddell’entropia incrociata come funzione obiettivo per problemi di classificazione

LogSoftMax, come discusso nella precedentemente, è un caso speciale di funzione di perdità basata sull’entropia incrociata (cross-entropy loss). In PyTorch, bisogna assicursarsi di fornire una funzione di perdità di entropia-incrociata con log softmax come input (al contrario della normale SoftMax).

Uso della discesa stocastica del gradiente con minibatch durante l’allenamento

Come discusso precedentemente, i minibatch permettono di addestrare i modelli più efficientemente perché vi è ridondanza nei dati; non c’è bisogno di fare predizioni e calcolare la perdita su ogni singola osservazione a ogni singolo passo dell’algoritmo per stimare il gradiente.

Mescolare l’ordine degli esempi per l’allenamento quando si usa la discesa stocastica del gradiente

L’ordine conta. Se il modello vede solo esempi di una singola classe durante ogni singolo passo d’addestramento, allora imparerà a predire la classe senza imparare perché dovrebbe essere predetta quella classe. Per esempio, se state provando a classificare le cifre dal dataset MNIST e i dati non sono ordinati, i parametri del bias nell’ultimo strato predirranno semplicemente sempre $0$, quindi si adatta a predire sempre $1$, poi $2$, ecc. Idealmente, dovrebbero esservi istanze di ogni classe in ogni minibatch.

Tuttavia, c’è ancora un dibattito in atto sulla necessità di variare l’ordine dei campioni ad ogni passo (epoca).

Normalizzare gli input per avere media zero e varianza unitaria

Prima dell’addestramento, è utile normalizzare ogni variabile di input, così da avere media $0$ e deviazione standard $0$. Quando si usano immagini codificate come RGB è comune prendere la media e la deviazione standard di ogni canale e normalizzare ogni singolo canale indipendentemente. Per esempio, si prende la media $m_b$ e la deviazione standard $\sigma_b$ di tutti i valori blu nel dataset, poi si normalizzano i valori blu di ogni singola immagine:

dove $\epsilon$ è un numero arbitrariarmente piccolo che si usa per evitare la divisione per $0$. Si ripete lo stesso procedimento per i canali verde e rosso. Questo è necessario per ottenere un segnale significativo dalle immagini in caso di diversa luminosità; Per esempio, le immagini illuminate di giorno hanno molto rosso, mentre le immagini sott’acqua quasi non ne hanno.

Uso di una scaletta per la diminuzione del tasso di apprendimento

Il tasso (o livello) di apprendimento dovrebbe diminuire con l’avanzamento dell’addestramento. In pratica, i modelli più avanzati sono addestrati usando algoritmi come Adam che adattano il tasso d’apprendimento invece del semplice SGD con un tasso d’apprendimento costante.

Uso della regolarizzazione L1 e/o L2 per il decadimento dei pesi

Si può aggiunere, alla funzione costo, un costo per i pesi di grossa entità. Per esempio, usando la regolarizzazione L2, noi vorremmo definire la perdita $L$ e aggiornare i pesi $w$ come segue:

Per capire perché questo è chiamato decadimento dei pesi, si noti che si può riscrive la formula sopra per mostrare come moltiplicando $w_i$ per una costante minore di uno durante l’aggiornamento

La regolarizzazione L1 (Lasso) è simile, salvo che usa $\sum_i \vert w_i\vert$ al posto di $\Vert w \Vert^2$.

Essenzialmente, la regolarizzaione prova a dire al sistema di minimizzare la funzione costo con un vettore dei pesi più corto possibile. Con la regolarizzazione L1 i pesi che non sono utili vengono ridotti a $0$.

Inizializzazione dei pesi

I pesi devono essere inizializzati causalmente; tuttavia, non dovrebbero essere né troppo grandi né troppo piccoli cosicché l’output abbia approssimativamente la stessa varianza dell’input. Ci sono vari accorgimenti per inizializzare i pesi in PyTorch. Un’inizializzazione che funziona bene per i modelli profondi è l’inizializzazione di Kaiming, dove la varianza dei pesi è inversamente proporzionale alla radice quadrata del numero di dati in input.

Uso del dropout

Il dropout è un altra forma di regolarizzazione. Può essere pensato come un altro strato della rete neurale: prende degli input, forza casualmente $n/2$ degli input a $0$, restituisce il risultato come output. Questo obbliga il sistema a ottenere l’informazione da tutte le unità in input, piuttosto che fare troppo affidamento a un numero piccolo di input, cosi da distrubuire l’informazione tra tutte le unità di uno strato. Questo metodo è stato inizialmente proposto da Hinton et al (2012).

Per altri accorgimenti, si veda LeCun et al 1998.

Infine, nota che la retropropagazione non funziona solo per i modelli con moduli a cascata; può funzionare per ogni grafo diretto aciclico finché vi è un ordine parziale dei moduli.