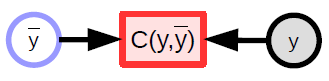Introduzione al gradient descent e alla retropropagazione

Gradient Descent optimization algorithm

Modelli parametrici

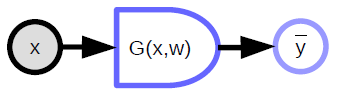
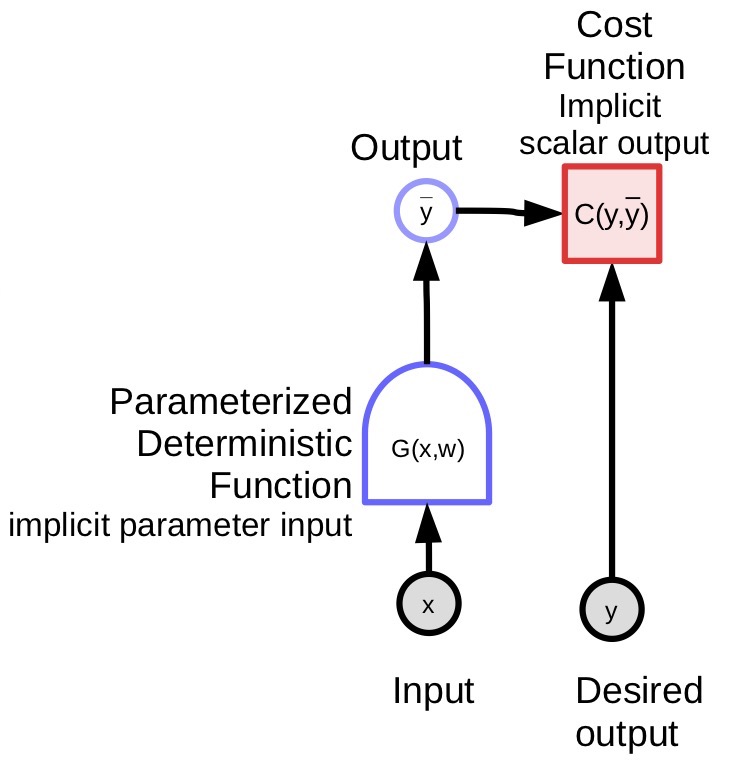
I modelli parametrici sono semplicemente funzioni che dipendono da input e parametri addestrabili. Non vi è alcuna differenza fondamentale tra i due, tranne per il fatto che i parametri addestrabili sono condivisi tra i campioni di addestramento, mentre l’input varia da campione a campione. Nella maggior parte dei framework di apprendimento profondo, i parametri sono impliciti, cioè non vengono passati quando viene chiamata la funzione. Sono “salvati all’interno della funzione”, per così dire, almeno nelle versioni orientate agli oggetti (object-oriented) dei modelli.

Il modello (funzione) parametrizzato accetta un input, ha un vettore di parametro e produce un output. Nell’apprendimento supervisionato, questo output viene passato alla funzione di costo ($ C (y, \bar {y} $)), che confronta l’output reale ($ {y} $) con l’output del modello ($ \bar {y} $ ). Il grafo computazionale per questo modello è mostrato nella Figura 1.

Figura 1: Rappresentazione del grafo computazionale per un modello parametrico

Esempi di funzioni parametriche -

• Modello lineare: Somma ponderata delle componenti del vettore di input:

  \[\bar{y} = \sum_i w_i x_i, C(y,\bar{y}) = \Vert y - \bar{y}\Vert^2\]

• Vicino più vicino (Nearest Neighbour) — Vi sono un input $\vect{x}$ e una matrice di peso $\matr{W}$ con ogni riga è indicizzata da $k$. L’output è il valore di $k$ che corrisponde alla riga di $\matr{W}$ più vicina a $\vect{x}$:

  \[\bar{y} = \underset{k}{\arg\min} \Vert x - w_{k,.} \Vert^2\]

  I modelli parametrici potrebbero anche utilizzare funzioni complicate.

Annotazioni del diagramma a blocchi per i grafi computazionali

• Variabili (tensori, scalari, continue, discrete)
  • è un input osservato del sistema
  • è una variabile calcolata prodotta da una funzione deterministica

• Funzioni deterministiche

  

  • Accetta input multipli e può produrre output multipli
  • Ha una variabile a parametro implicito (${w}$)
  • Il lato arrotondato indica la direzione in cui è facile da calcolare. Nel diagramma qui sopra, è più facile calcolare ${\bar{y}}$ da ${x}$ rispetto al contrario

• Funzione a valore scalare

  

  • Utilizzata per rappresentare le funzioni di costo
  • Ha un output scalare implicito
  • Accetta più input e genera un singolo valore in uscita (normalmente la distanza fra gli input)

Funzioni di perdita (Loss Functions)

La funzione di perdita è una funzione da minimizzare durante l’allenamento. Esistono due tipi di perdite:

1) Perdita per singola istanza

2) Perdita media

Per ogni insieme di istanze

La perdita media su un insieme $S$ è data da:

Figura 2: grafo computazionale per un modello con perdita media (*average loss*)

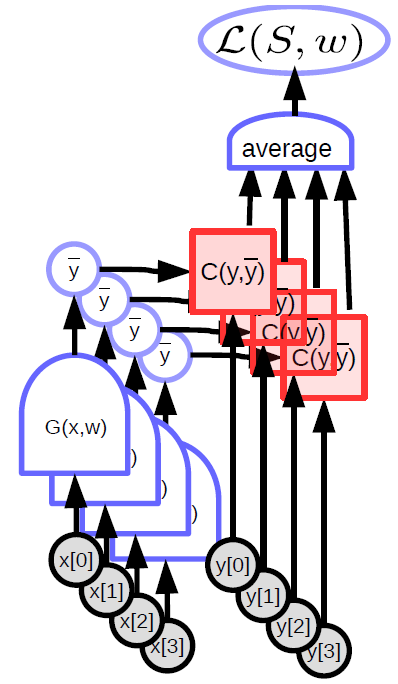Nel paradigma classico di apprendimento supervisionato (Supervised Learning), la perdita (per istanza) è semplicemente l’output della funzione di costo. L’apprendimento automatico (Machine Learning) riguarda principalmente l’ottimizzazione delle funzioni (generalmente, la minimizzazione di esse). Potrebbe anche implicare la ricerca degli equilibri di Nash tra due funzioni come con le GAN (reti generative avversarie, Generative Adversarial Networks). Questo viene fatto usando i metodi basati sul gradiente, non necessariamente la discesa del gradiente (Gradient Descent).

Discesa del Gradiente (Gradient Descent)

Un metodo basato sul gradiente (Gradient-Based Method) è un metodo/algoritmo che trova il minimo della funzione, assumendo che si possa facilmente calcolare il gradiente di quella funzione. Si assume che la funzione sia continua e differenziabile quasi ovunque (non è necessario che lo sia ovunque).

Descrizione intuitiva della Discesa del Gradiente – Immagina di essere in montagna nel mezzo di una notte nebbiosa. Dato che vuoi andare al villaggio e hai una visione limitata, ti guardi intorno nelle immediate vicinanze per trovare la direzione della discesa più ripida e fai un passo in quella direzione.

Metodi differenti della Discesa del Gradiente

• Regola di aggiornamento della discesa gradiente a batch completo: \(w \leftarrow w - \eta \frac{\partial L(S,w)}{\partial w}\)

• Per la SGD (discesa stocastica del gradiente, Stochastic Gradient Descent), la regola di aggiornamento diventa:

  • Scegliere un $p \in \lbrace 0, \cdots, P-1 \rbrace$, poi aggiornare

    \[w \leftarrow w - \eta \frac{\partial L(x[p], y[p],w)}{\partial w}\]

Dove ${w}$ rappresenta il parametro che deve essere ottimizzato.

$\eta$ è una costante qui, ma, in algoritmi più sofisticati, potrebbe essere una matrice.

Se è una matrice positiva semi-definita, ci sposteremo comunque in discesa ma non necessariamente nella direzione della discesa più ripida. In effetti la direzione della discesa più ripida potrebbe non sempre essere la direzione in cui vogliamo spostarci.

Se la funzione non è differenziabile, ovvero ha un “buco” o presenta “scalini” o è piatta, situazioni in cui il gradiente non fornisce alcuna informazione, è necessario ricorrere ad altri metodi, chiamati metodi di ordine 0 (0-th Order Methods) o metodi non basati sul gradiente (Gradient-Free Methods). L’apprendimento profondo si basa interamente su metodi basati sul gradiente.

Tuttavia, il RL (apprendimento per rinforzo, Reinforcement Learning) richiede la Stima del gradiente (Gradient Estimation) senza una forma esplicita per il gradiente. Un esempio è un robot che impara ad andare in bicicletta; il robot cade di tanto in tanto. La funzione obiettivo misura per quanto tempo la bici rimane in piedi senza cadere. Sfortunatamente, non esiste un gradiente per la funzione obiettivo. Il robot deve affidarsi ad algoritmi differenti.

La funzione di costo del RL non è usualmente differenziabile, ma la rete che calcola l’output è basata sul gradiente. Questa è la differenza principale tra apprendimento supervisionato e apprendimento per rinforzo. In quest’ultimo, la funzione di costo $C$ non è differenziabile. In realtà è completamente sconosciuta. Restituisce semplicemente un output quando gli input le vengono passati, come una scatola nera. Ciò rende l’RL altamente inefficiente: ciò è uno dei suoi principali inconvenienti, in particolare quando il vettore dei parametri è ad elevata dimensionalità (il che implica un enorme spazio delle soluzioni in cui cercare, rendendo difficile trovare un verso in cui muoversi).

Una tecnica molto popolare nel RL sono gli Actor Critic Methods (metodi Attore-Critico). Un metodo critico consiste fondamentalmente di un secondo modulo C che è un modulo noto e addestrabile. Si può addestrare il modulo C, che è differenziabile, per approssimare la funzione di costo/ricompensa. La ricompensa è un costo negativo, più simile a una punizione. Questo è un modo per rendere la funzione di costo differenziabile, o almeno per approssimarla con una funzione differenziabile in modo che vi si possa effettuare la retropropagazione.

Vantaggi della SGD e della retropropagazione per le reti neurali tradizionali

Vantaggi della discesa stocastica del gradiente

In pratica, si usa il gradiente stocastico per calcolare il gradiente della funzione obiettivo rispetto ai parametri. Invece di calcolare l’intero gradiente, calcolato come media su tutte le istanze, della funzione obiettivo, il gradiente stocastico considera solo un’istanza, calcola la perdita ,$L$, e il gradiente della perdita rispetto ai parametri, quindi fa un passo nella direzione del gradiente negativo.

Nella formula, $w$ viene approssimato da $w$ meno la dimensione del passo, moltiplicato per il gradiente della funzione di perdita della singola istanza rispetto ai parametri, ($x[p]$,$y[p]$).

Se lo facciamo su un singolo campione, otterremo una traiettoria molto rumorosa, come mostrato nella Figura 3. Anziché seguire direttamente la discesa, la direzione è stocastica. Ogni istanza porterà la perdita in una direzione diversa. In media, ci dirigeremo verso il minimo. Sebbene appaia inefficiente, è molto più veloce della discesa del gradiente a batch completo almeno nel contesto dell’apprendimento automatico quando le istanze dei dati presentano una certa ridondanza.

Figure 3: Traiettoria della discesa stocastica del gradiente nel caso di aggiornamento per singola istanza

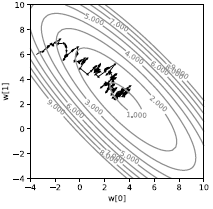Nella pratica, si utilizzano dei batch invece di eseguire la discesa stocastica del gradiente su un a singola istanza. Calcoliamo la media del gradiente su un lotto (batch, campione casuale) di istanze, dopodiché facciamo un passo nella direzione del gradiente negativo. L’unico motivo per farlo è che possiamo usare in modo più efficiente l’hardware esistente (ad esempio GPU, CPU multicore) se utilizziamo i batch, poiché è più facile parallelizzare.

Reti neurali tradizionali

Le reti neurali tradizionali sono fondamentalmente strati intervallati di operazioni lineari e operazioni non-lineari puntuali (monodimensionali). Le operazioni lineari sono concettualmente una moltiplicazione matrice-vettore. Prendiamo il vettore (input) moltiplicato per una matrice contenente i pesi. Il secondo tipo di operazione consiste nel prendere tutte le componenti del vettore risultante e passarlo attraverso una semplice funzione non-lineare (ad esempio, $\texttt{ReLU}(\cdot)$, $\tanh(\cdot)$, …).

Figura 4: Reti neurali tradizionali

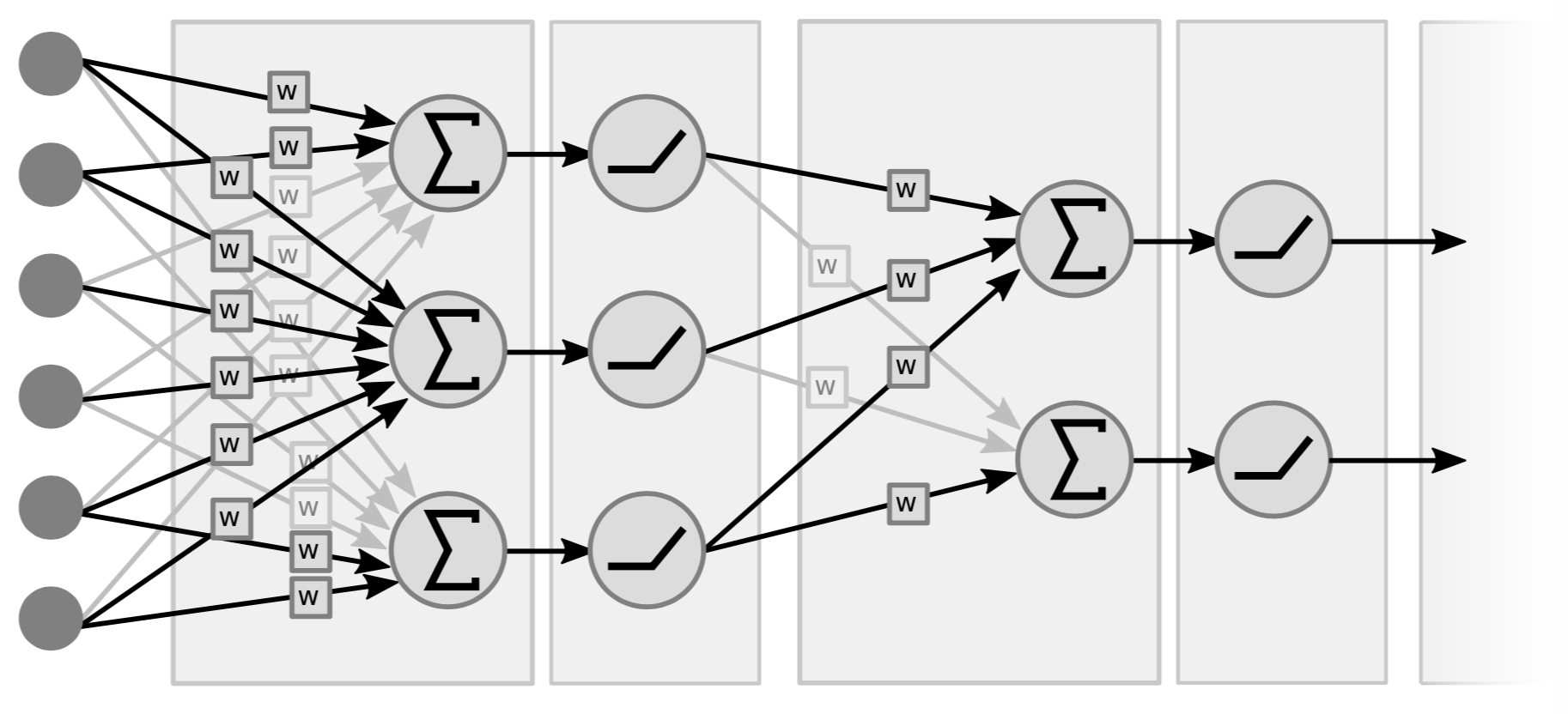La Figura 4 è un esempio di una rete a 2 strati, perché si contano le coppie linearità—non-linearità. Alcune persone lo chiamano una rete a 3 strati perché contano le variabili. Si noti che se non ci fossero non-linearità nel mezzo, potremmo anche riassumere il tutto in un singolo strato (con pesi diversi), perché il prodotto di due funzioni lineari è una funzione lineare.

La figura 5 mostra come si combinano i blocchi funzionali lineari e non-lineari della rete:

Figure 5: Guardando all'interno dei blocchi lineari e non-lineari

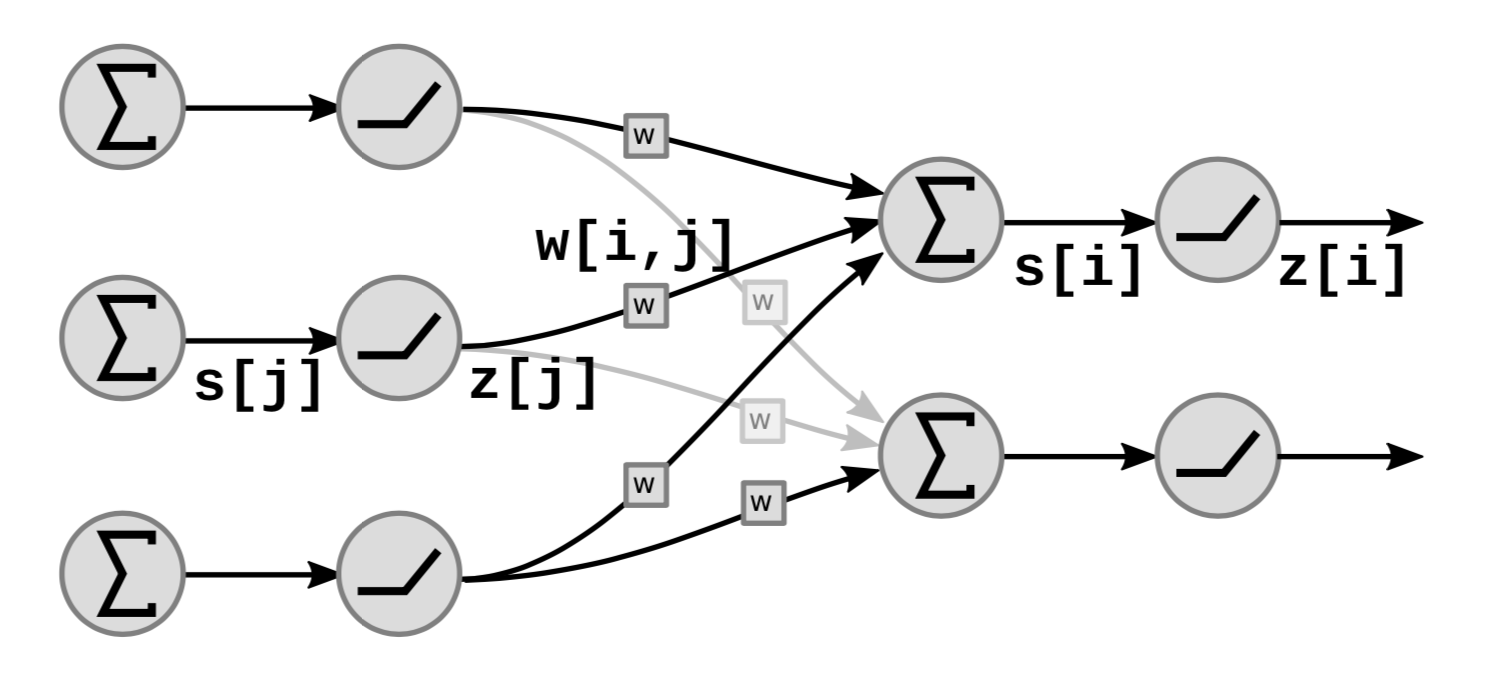Nel grafo, $s[i]$ è la somma pesata dell’unità ${i}$ che è calcolata come:

dove $UP(i)$ denota i predecessori di $i$ e $z[j]$ è la $j$-esima uscita dallo strato precedente.

L’uscita $z[i]$ è calcolata come:

dove $f$ è una funzione non-lineare.

Retropropagazione (backpropagation) attraverso una funzione non-lineare

Il primo modo per eseguire la retropropagazione è retropropagare attraverso una funzione non-lineare. Prendiamo una particolare funzione non lineare $h$ dalla rete e lasciamo tutto il resto all’interno di una “scatola nera”.

Figura 6: Retropropagazione attraverso una funzione non-lineare

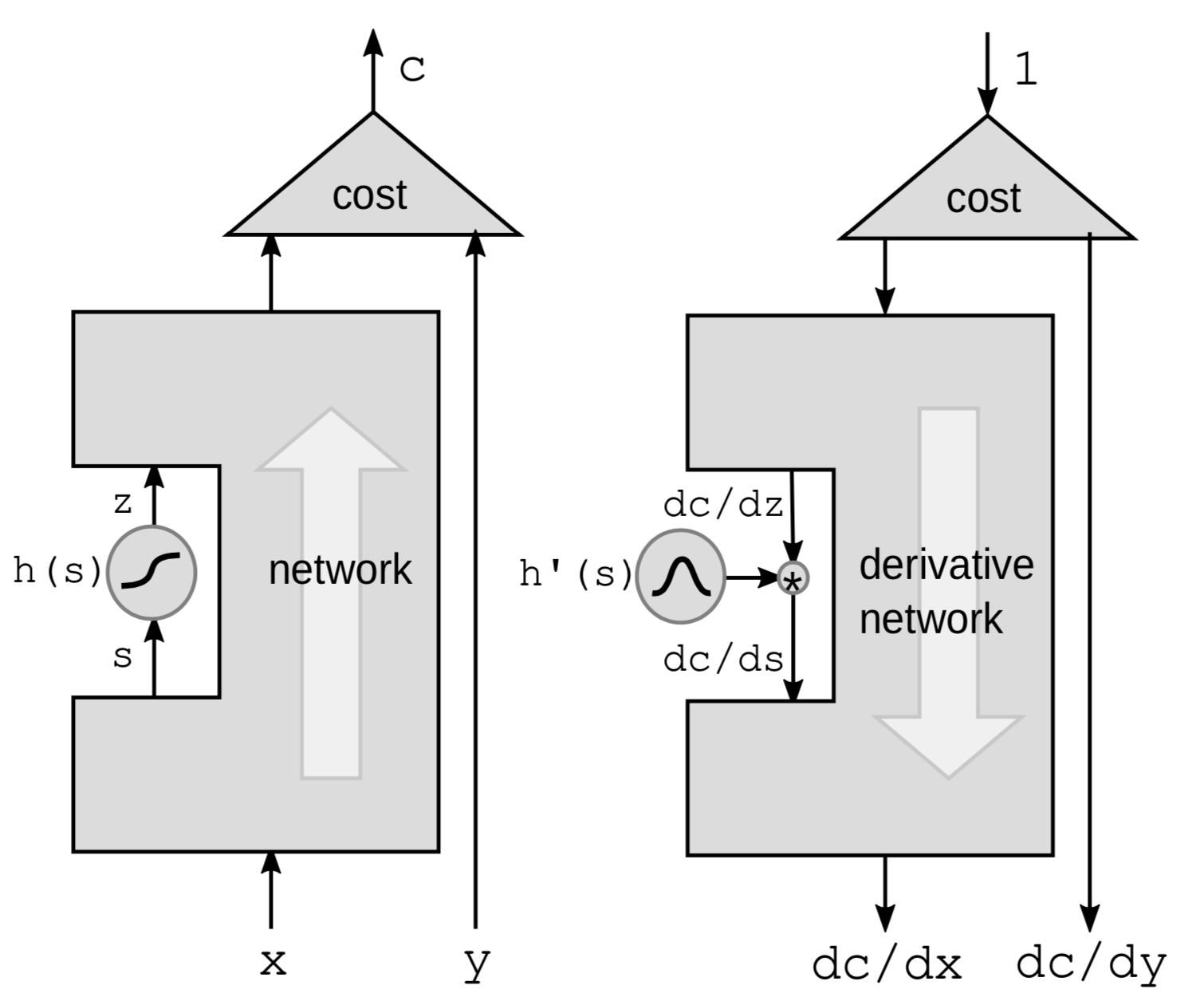Useremo la regola della derivata delle funzioni composte (chain rule) per calcolare i gradienti:

dove $h’(s)$ è la derivata di $z$ rispetto a $s$, rappresentata nella formula da $\frac{\mathrm{d}z}{\mathrm{d}s}$. Per chiarire la connessione fra le derivate, riscriviamo la formula sopra come:

Quindi, se abbiamo una composizione di queste funzioni nella rete, possiamo retropropagare moltiplicando a catena le derivate di tutte le funzioni ${h}$ una dopo l’altra fino in fondo.

È più intuitivo pensarlo in termini di perturbazioni. Perturbando $s$ da $\mathrm{d}s$, $z$ verrà perturbato da:

Questo a sua volta perturberebbe $C$ da:

Nuovamente, otteniamo la stessa formula già prima derivata.

Retropropagazione attraverso una somma pesata

Per un modulo lineare, eseguiamo la retropropagazione attraverso una somma ponderata. Qui vediamo l’intera rete come una scatola nera ad eccezione di 3 connessioni che vanno da una variabile ${z}$ a un gruppo di variabili $s$.

Figura 7: Retropropagazione attraverso una somma pesata

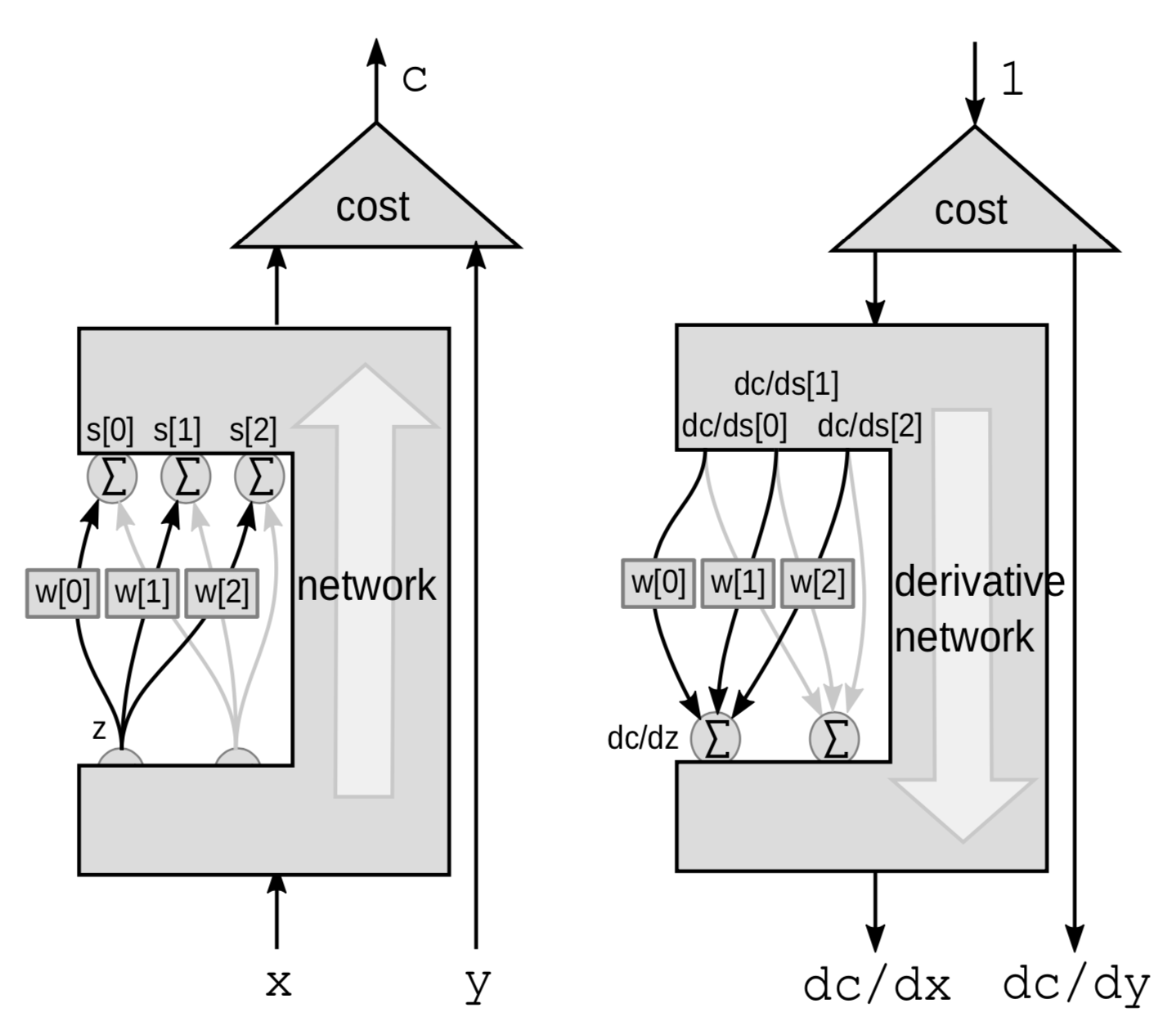Questa volta la perturbazione è una somma ponderata. $Z$ influenza diverse variabili. Perturbando $z$ da $\mathrm{d}z$, $s[0]$, $s[1]$ e $s[2]$ saranno perturbati da:

Questo perturberà $C$ tramite

Quindi $C$ varierà a causa della somma di 3 variazioni:

Implementazione in PyTorch di reti neurali e un algoritmo generalizzato di retropropagazione

Diagramma a blocchi di una rete neurale tradizionale

• Blocchi lineari $s_{k+1}=w_kz_k$

• Blocchi non-lineari $z_k=h(s_k)$

  

$w_k$: matrici $z_k$: vettori $h$: applicazione della funzione scalare ${h}$ a ogni componente. Questa è una rete neurale a 3 strati con coppie di funzioni lineari e non lineari, sebbene la maggior parte delle reti neurali moderne non abbia separazioni lineari e non-lineari così chiare e siano più complesse.

Implementazione PyTorch

import torch
from torch import nn
image = torch.randn(3, 10, 20)
d0 = image.nelement()

class mynet(nn.Module):
    def __init__(self, d0, d1, d2, d3):
        super().__init__()
        self.m0 = nn.Linear(d0, d1)
        self.m1 = nn.Linear(d1, d2)
        self.m2 = nn.Linear(d2, d3)

    def forward(self,x):
        z0 = x.view(-1)  # appiattimento del vettore di input
        s1 = self.m0(z0)
        z1 = torch.relu(s1)
        s2 = self.m1(z1)
        z2 = torch.relu(s2)
        s3 = self.m2(z2)
        return s3
model = mynet(d0, 60, 40, 10)
out = model(image)

• Possiamo implementare reti neurali con classi orientate agli oggetti in PyTorch. Per prima cosa definiamo una classe per la rete neurale e inizializziamo gli strati lineari nel costruttore usando la classe predefinita nn.Linear. Gli strati “lineari” devono essere oggetti separati perché ognuno di essi contiene un vettore di parametri. La classe nn.Linear aggiunge anche implicitamente il vettore di distorsione (bias). Definiamo poi una funzione in avanti (forward) che descrive come calcolare gli output tramite la funzione $\text{torch.relu}$ come attivazione non-lineare. Non è necessario inizializzare funzioni relu separate perché esse non hanno parametri.

• Non abbiamo bisogno di calcolare noi stessi il gradiente poiché PyTorch sa come retropropagare e calcolare i gradienti una volta data la funzione forward.

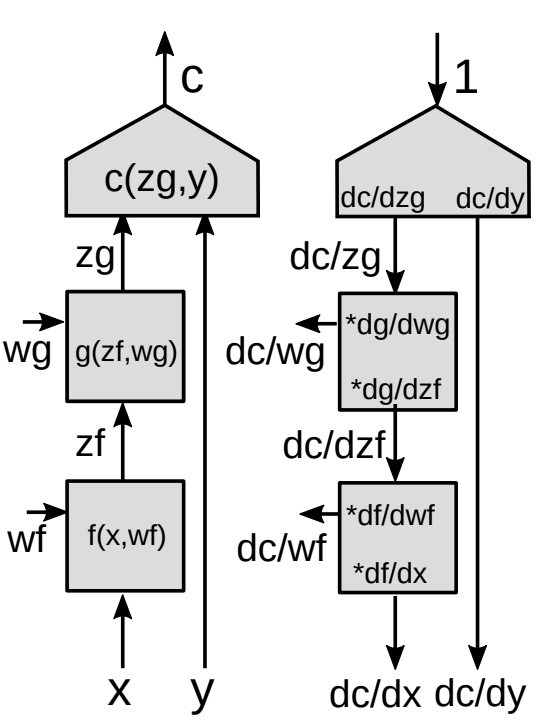
Retropropagazione attraverso un modulo funzionale

Ora noi presentiamo una forma più generalizzata di retropropagazione.

Figure 8: Retropropagazione attraverso un modulo funzionale

• Usando la regola della derivata della composta per funzioni vettoriali

  \[z_g : [d_g\times 1]\] \[z_f:[d_f\times 1]\] \[\frac{\partial c}{\partial{z_f}}=\frac{\partial c}{\partial{z_g}}\frac{\partial {z_g}}{\partial{z_f}}\] \[[1\times d_f]= [1\times d_g]\times[d_g\times d_f]\]

  Questa è la formula di base per calcolare $\frac{\partial c}{\partial{z_f}}$ usando la regola della derivata della composta. Si noti che il gradiente di una funzione scalare rispetto a un vettore è a sua volta un vettore della stessa dimensione del vettore rispetto al quale si differenzia. Per rendere coerenti le notazioni, si tratta di un vettore di riga anziché di un vettore colonna.

• Matrice jacobiana

  \[\left(\frac{\partial{z_g}}{\partial {z_f}}\right)_{ij}=\frac{(\partial {z_g})_i}{(\partial {z_f})_j}\]

  Abbiamo bisogno di $\frac{\partial {z_g}}{\partial {z_f}}$ (elementi della matrice jacobiana) per calcolare il gradiente della funzione di costo rispetto a $z_f$ dato lo stesso gradiente rispetto a $z_g$. Ogni elemento $ij$ è uguale alla derivata parziale della $i$-esima componente del vettore di output rispetto alla $j$-esima componente del vettore di input.

  Se abbiamo una cascata di moduli, scendendo continuiamo a moltiplicare le matrici jacobiane di tutti i moduli e otteniamo i gradienti rispetto a tutte le variabili interne.

Retropropagazione attraverso un grafo a più stadi

Si consideri una cascata di molti moduli in una rete neurale come da Figura 9.

Figura 9: Retropropagazione attraverso un grafo a più stadi

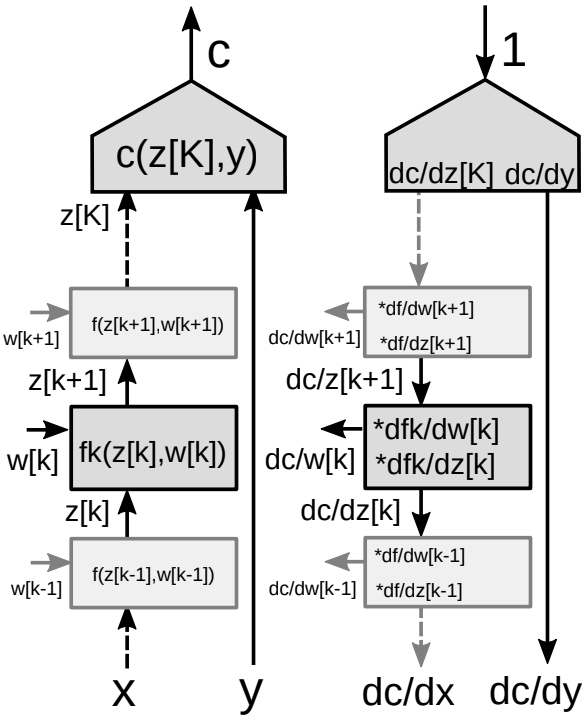Per l’algoritmo di retropropagazione, abbiamo bisogno di due gruppi di gradienti: gradiente rispetto agli stati (ogni modulo della rete) e gradiente rispetto ai pesi (tutti i parametri in un particolare modulo). Quindi abbiamo due matrici jacobiane associate a ciascun modulo. Possiamo di nuovo usare la regola della derivata della composta per la retropropagazione.

• Usando la regola della derivata della composta per le funzioni vettoriali

  \[\frac{\partial c}{\partial {z_k}}=\frac{\partial c}{\partial {z_{k+1}}}\frac{\partial {z_{k+1}}}{\partial {z_k}}=\frac{\partial c}{\partial {z_{k+1}}}\frac{\partial f_k(z_k,w_k)}{\partial {z_k}}\] \[\frac{\partial c}{\partial {w_k}}=\frac{\partial c}{\partial {z_{k+1}}}\frac{\partial {z_{k+1}}}{\partial {w_k}}=\frac{\partial c}{\partial {z_{k+1}}}\frac{\partial f_k(z_k,w_k)}{\partial {w_k}}\]

• Due matrici jacobiane per il modulo

  • Una rispetto a $z[k]$
  • Una rispetto a $w[k]$