Motivazione, Algebra Lineare, Visualizzazione

Risorse

Segui Alfredo Canziani su Twitter @alfcnz. Si possono trovare video e libri di testo con dettagli rilevanti sull’algebra lineare e sulla decomposizione del valore singolare (singular value decomposition, SVD) cercando nei tweet di Alfredo, ad esempio linear algebra (from:alfcnz) nella casella di ricerca.

Trasformazioni e motivazione

Come esempio motivante, consideriamo la classificazione delle immagini. Supponiamo di scattare una foto con una fotocamera da 1 megapixel. Questa immagine avrà circa 1.000 pixel in verticale e 1.000 pixel in orizzontale e ogni pixel avrà tre dimensioni di colore rosso, verde e blu (RGB). Ogni immagine particolare può quindi essere considerata come un punto in uno spazio di 3 milioni di dimensioni. Con una così grande dimensionalità, molte immagini interessanti che potremmo voler classificare – come un cane in confonto a un gatto – saranno essenzialmente nella stessa regione dello spazio.

Al fine di separare efficacemente queste immagini, consideriamo i modi per trasformare i dati al fine di spostare i punti. Ricordiamo che nello spazio 2D, una trasformazione lineare è lo stesso della moltiplicazione di matrici. Ad esempio, le seguenti sono trasformazioni lineari:

• Rotation, Rotazione (quando la matrice è ortonormale).
• Scaling, Ridimensionamento (quando la matrice è diagonale).
• Reflection, Riflessione (quando il determinante è negativo).
• Shearing, Tosatura.

Nota che la traslazione da sola non è lineare poiché 0 non sarà sempre mappato su 0, ma è una trasformazione affine. Tornando al nostro esempio di immagine, possiamo trasformare i data points traslandoli in modo tale che i punti siano raggruppati attorno a 0 e ridimensionati con una matrice diagonale in modo tale da “zoomare” su quella regione. Infine, possiamo fare una classificazione trovando linee attraverso lo spazio che separano i diversi punti nelle rispettive classi. In altre parole, l’idea è quella di utilizzare trasformazioni lineari e non lineari per mappare i punti in uno spazio in modo che siano linearmente separabili. Questa idea sarà resa più concreta nelle seguenti sezioni.

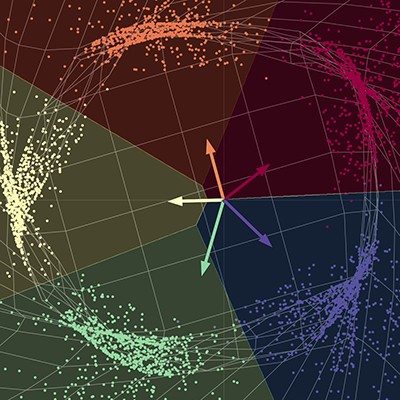
Visualizzazione dei dati - separazione dei punti per colore tramite una rete

Nella nostra visualizzazione, abbiamo cinque rami di una spirale, con ogni ramo corrispondente a un colore diverso. I punti vivono in un piano bidimensionale e possono essere rappresentati come una tupla; il colore rappresenta una terza dimensione che può essere considerata come le diverse classi per ciascuno dei punti. Quindi utilizziamo la rete per separare ciascuno dei punti in base al colore.

(a) Input points, pre-network	(b) Output points, post-network

La rete “allunga” il tessuto spaziale per separare ciascuno dei punti in sottospazi diversi. Alla convergenza, la rete separa ciascuno dei colori in diversi sottospazi del collettore finale. In altre parole, ciascuno dei colori in questo nuovo spazio sarà linearmente separabile usando una regressione uno contro tutti. I vettori nel diagramma possono essere rappresentati da una matrice cinque per due; questa matrice può essere moltiplicata per ogni punto per restituire i punteggi per ciascuno dei cinque colori. Ciascuno dei punti può quindi essere classificato per colore usando i rispettivi punteggi. Qui, la dimensione di output è cinque, una per ciascuno dei colori e la dimensione di input è due, una per le coordinate xey di ciascuno dei punti. Per ricapitolare, questa rete prende sostanzialmente il tessuto spaziale ed esegue una trasformazione dello spazio parametrizzata da più matrici e quindi da non linearità.

Architettura di rete

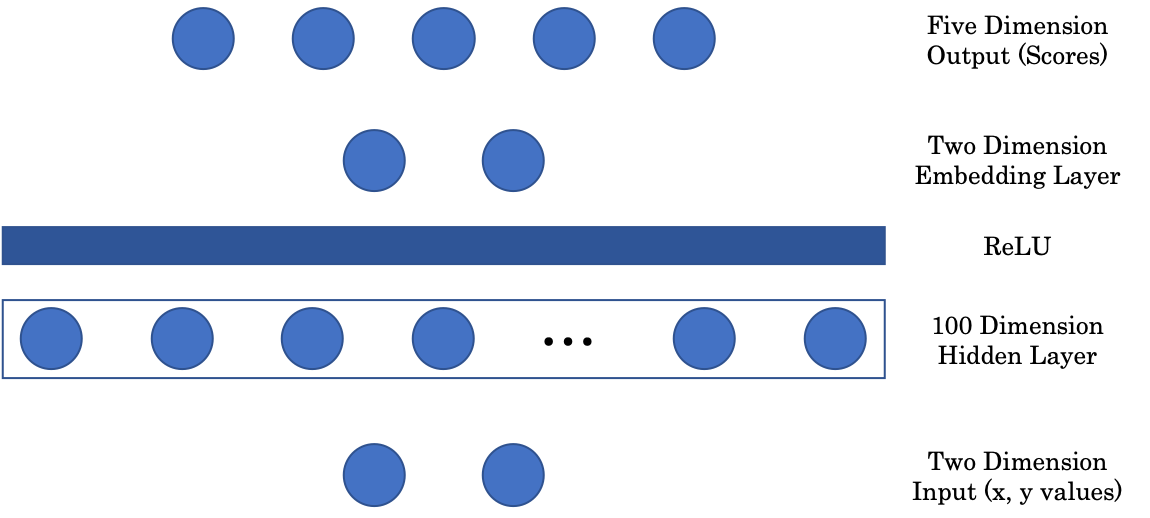
Figure 2: Network Architecture

La prima matrice mappa l’input bidimensionale su uno strato nascosto intermedio di 100 dimensioni. Abbiamo quindi uno strato non lineare, ReLU o Unità lineare rettificata, che è semplicemente la parte positiva della funzione $(\cdot)^+$ . Successivamente, per visualizzare la nostra immagine in una rappresentazione grafica, includiamo un livello di incorporamento che mappa l’input del livello nascosto 100 dimensionale su un output bidimensionale. Infine, il livello di incorporamento viene proiettato sul livello finale, a cinque dimensioni (livelli) della rete, che rappresenta un punteggio per ciascun colore.

Proiezioni casuali - Jupyter Notebook

Il Notebook Jupyter si trova qui. Per eseguire il notebook, assicurarsi di disporre dell’ambiente pDL installato come specificato nel README.md.

PyTorch device

PyTorch si può eseguire sia nella CPU che nella GPU di un computer. La CPU is utile per compiti (task) sequenziali, mentre la GPU è utile per compiti eseguiti in parallelo. Prima di eseguire sul dispositivo desiderato, dobbiamo prima assicurarci che i nostri tensori e modelli siano trasferiti nella memoria del dispositivo. Questo può essere fatto con le seguenti due righe di codice:

device = torch.device("cuda:0" if torch.cuda.is_available() else "cpu")
X = torch.randn(n_points, 2).to(device)

La prima linea crea una variabile chiamata device, che è assegnata alla GPU, se disponibile; altrimenti, per impostazione predefinita è assegnata alla CPU. Nella linea seguente , viene creato un tensore ed è inviato all memoria del device con la chiamata .to(device).

Suggerimenti per il Notebook Jupyter

Per vedere la documentazione di una funzione in una cella del noteboook, usare Shift + Tab.

Visualizzare le trasformazioni lineari

Ricordiamo che una trasformazione lineare può essere rappresentata come una matrice. Usando la scomposizione del valore singolare, possiamo scomporre questa matrice in matrici a tre componenti, ognuna delle quali rappresenta una diversa trasformazione lineare.

Nella eq. (1), le matrici $U$ e $V^\top$ sono ortogonali e rappresentano trasformazioni di rotazione e riflessione. La matrice centrale è diagonale e rappresenta una trasformazione in scala.

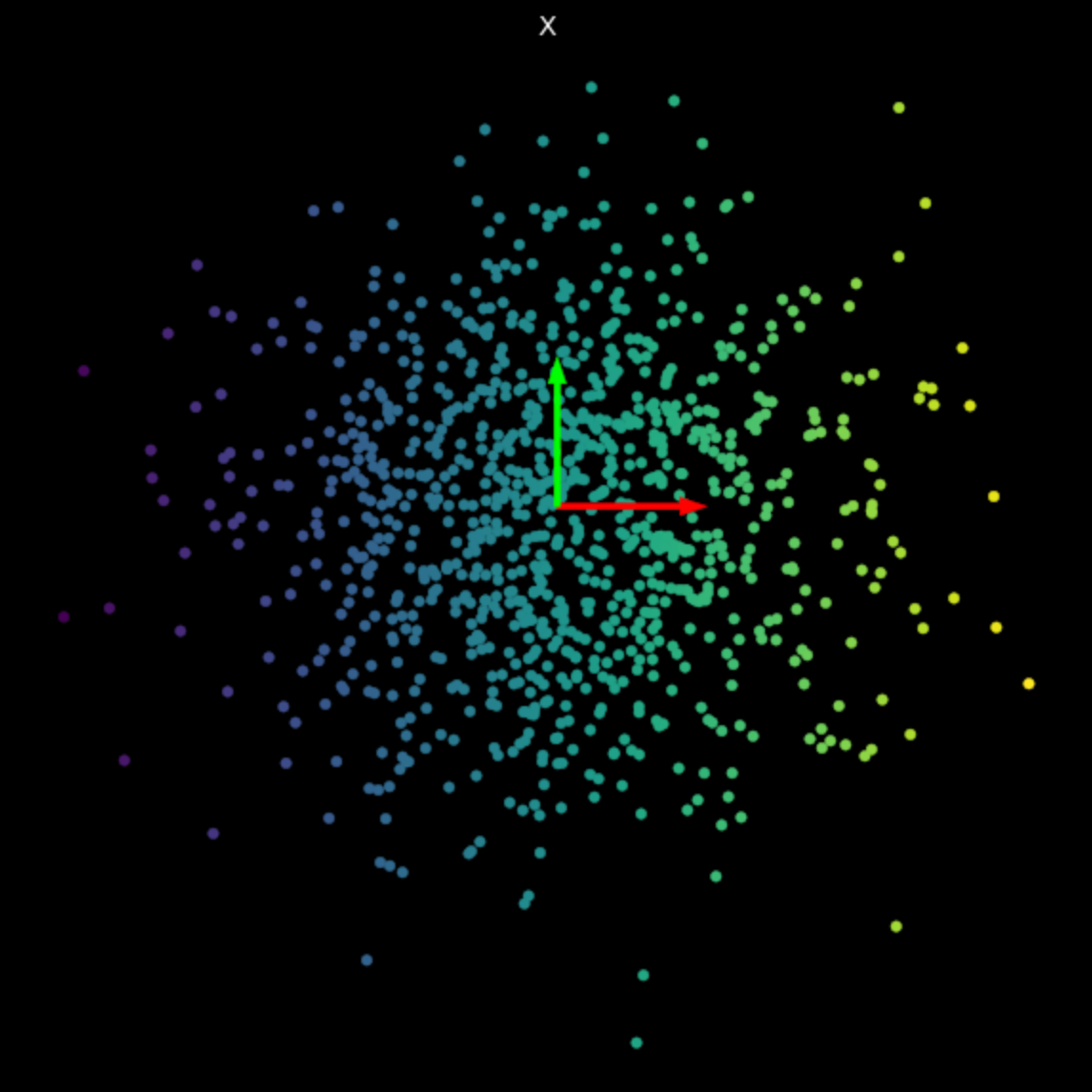
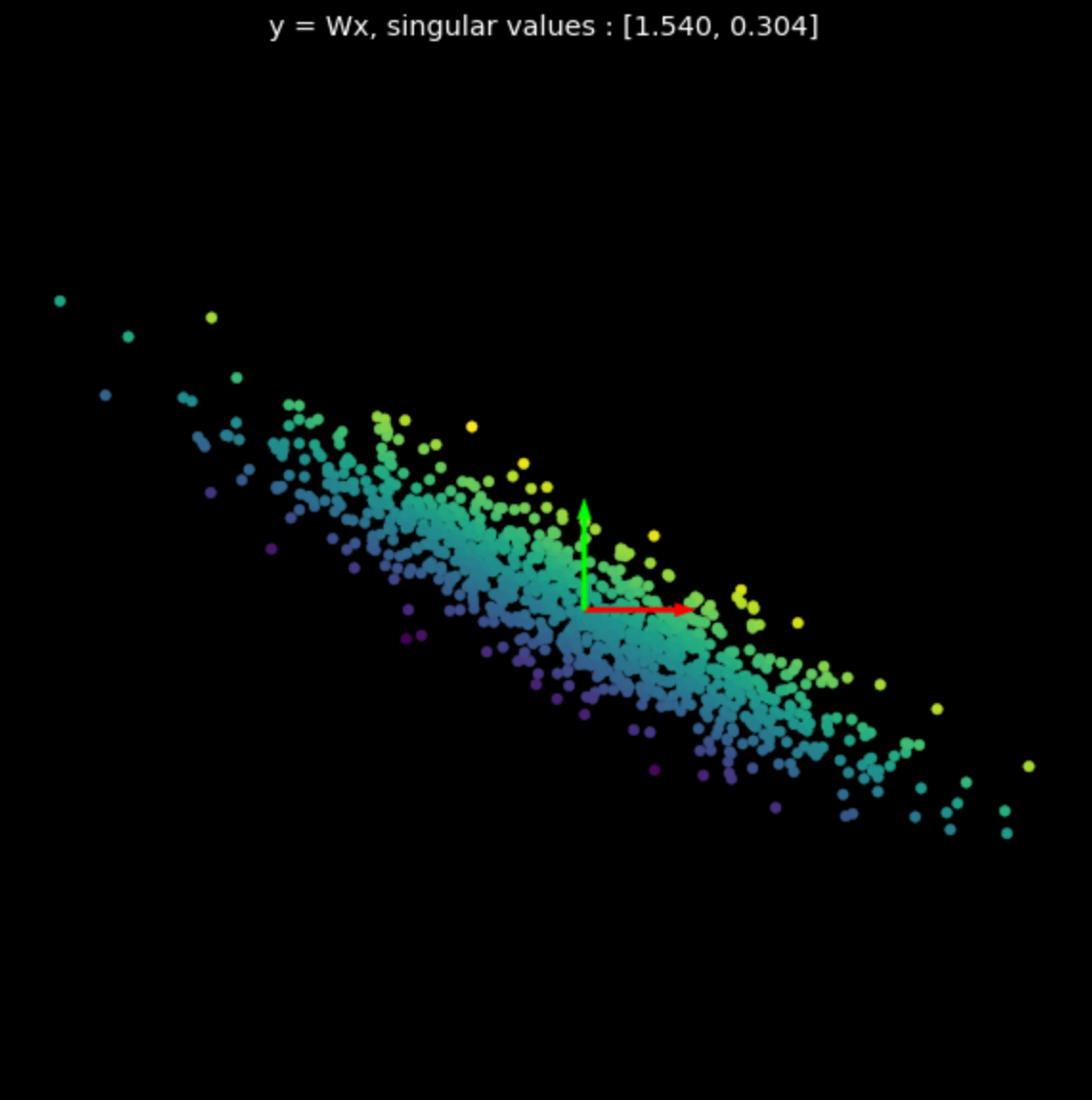
Visualizziamo le trasformazioni lineari di più matrici casuali in Fig. 3. Notare l’effetto dei valori singolari sulle trasformazioni risultanti.

Le matrici usate sono state generate con Numpy; tuttavia, si può usare anche la classe di PyTorch nn.Linear con bias = False per creare la trasformazione lineare.

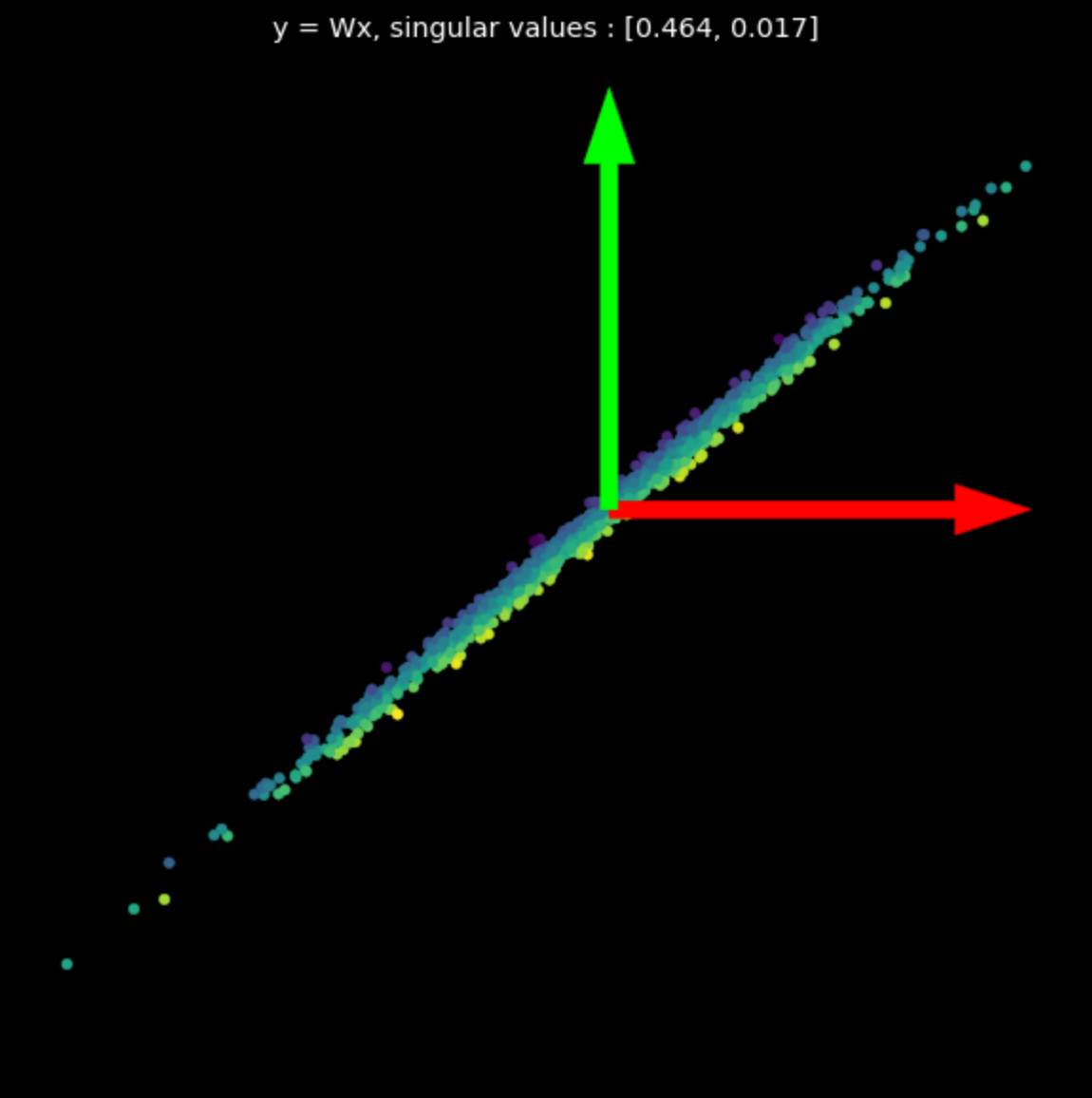(a) Original points	(b) $s_1$ = 1.540, $s_2$ = 0.304	(c) $s_1$ = 0.464, $s_2$ = 0.017

Transformationi non-lineari

Di seguito, visualizziamo la seguente trasformazione:

Richiamo del grafico di $\tanh(\cdot)$ in Fig. 4.

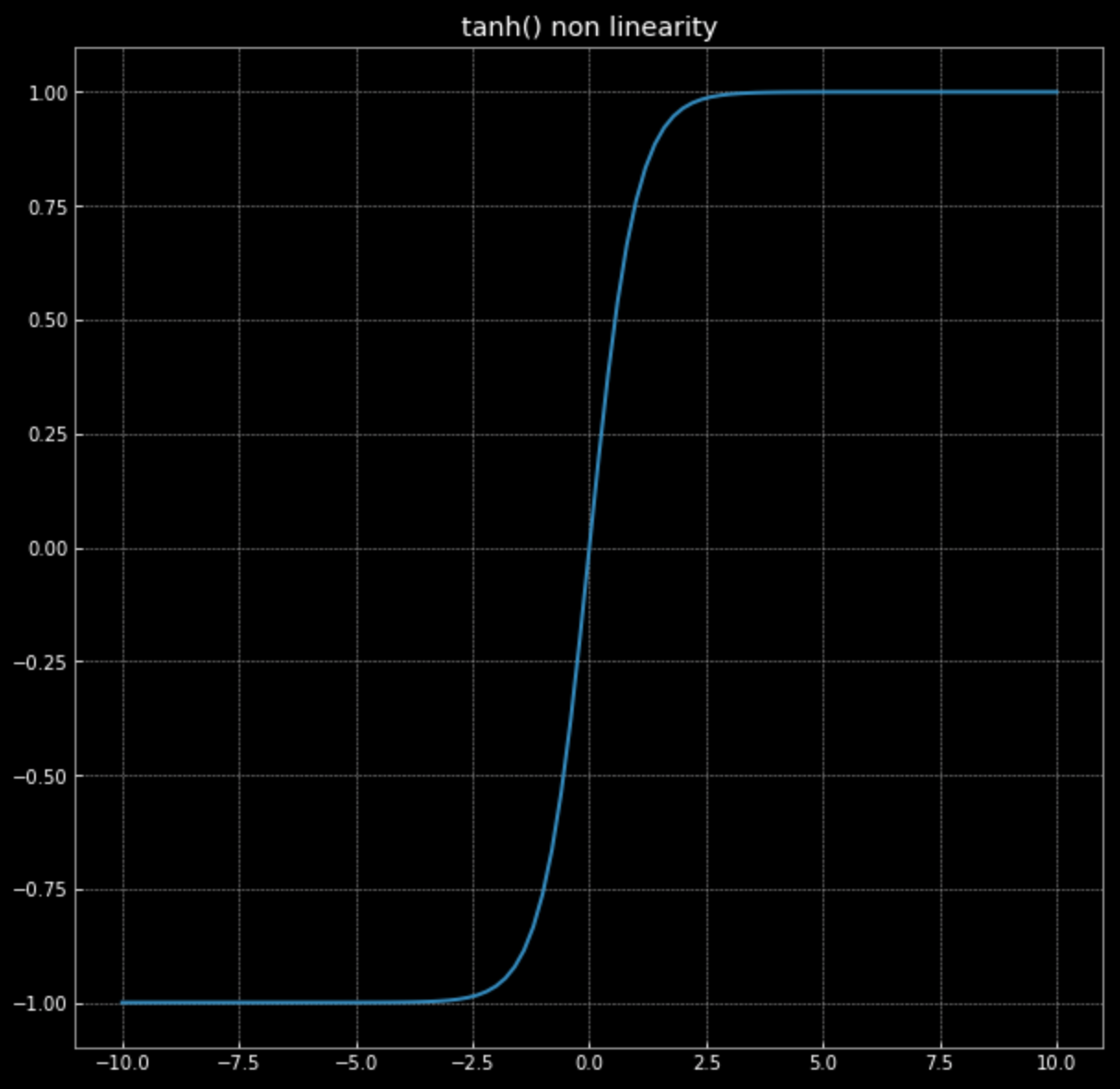
Figura 4: Non-linearità della tangente hiperbolica

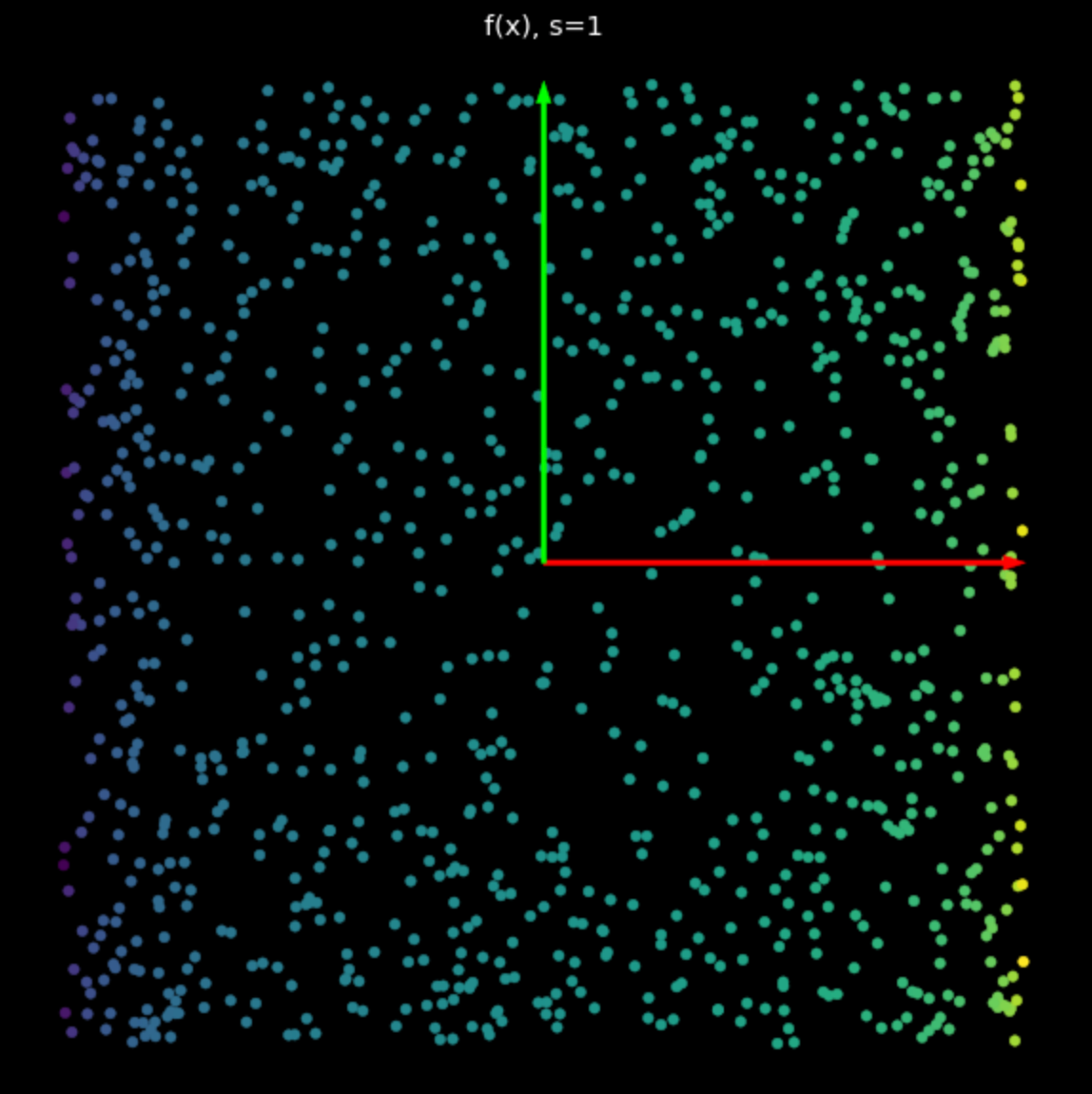
L’effetto di questa non linearità è di legare i punti tra $ -1 $ e $ + 1 $, creando un quadrato. Come valore di $ s $ in eq. (2) aumenta, sempre più punti vengono spinti verso il bordo del quadrato. Questo è mostrato in Fig. 5. Forzando più punti sul bordo, li allarghiamo di più e possiamo quindi tentare di classificarli.

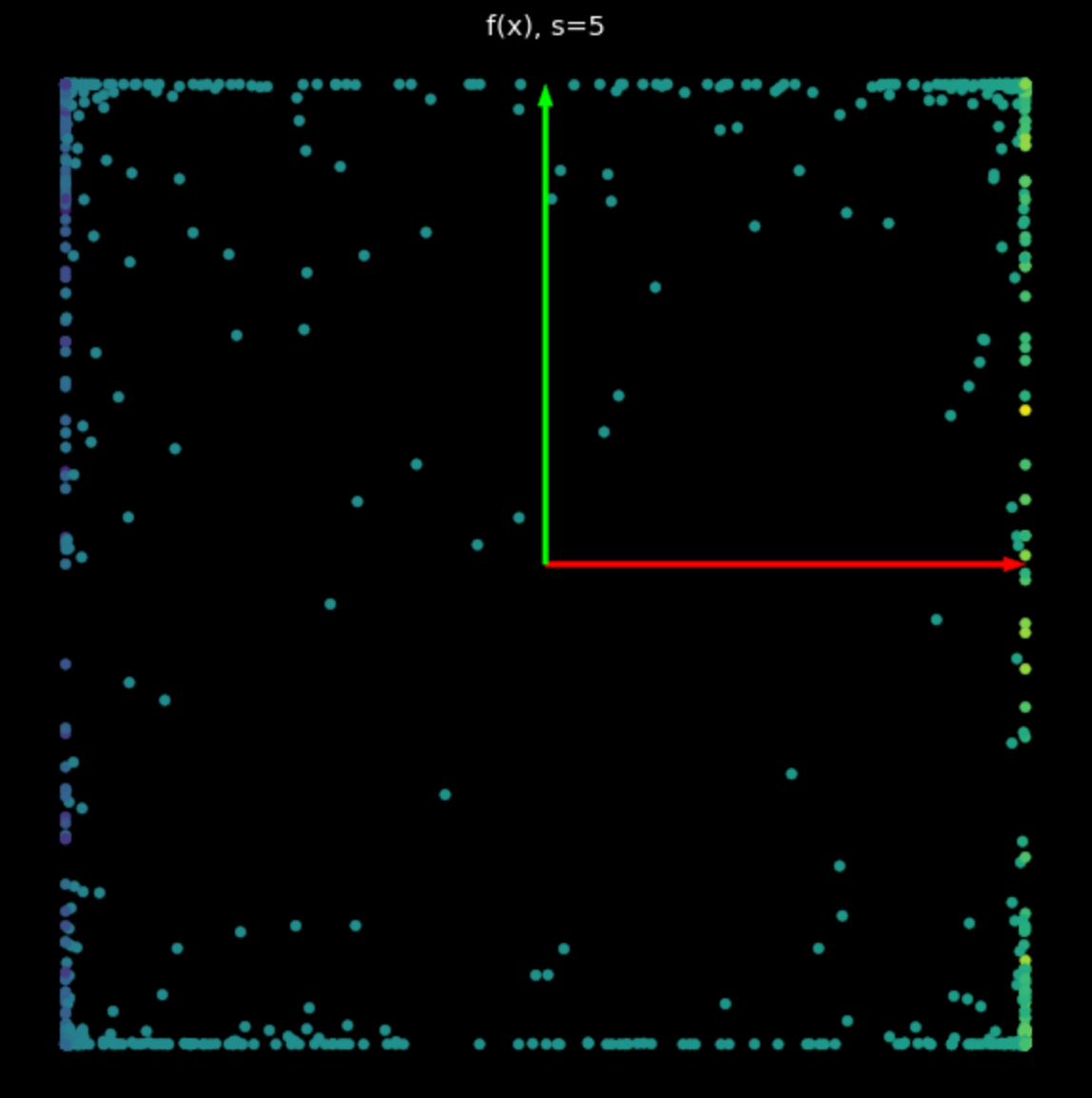(a) Non-linearità con $s=1$	(b) Non-linearità con $s=5$

Reti neurali causali

Infine, visualizziamo la trasformazione eseguita da una rete neurale semplice e non addestrata. La rete è costituita da uno strato lineare, che esegue una trasformazione affine, seguito da una non linearità tangente iperbolica e infine un altro strato lineare. Esaminando la trasformazione in Fig. 6, vediamo che è diverso dalle trasformazioni lineari e non lineari viste in precedenza. Andando avanti, vedremo come rendere queste trasformazioni eseguite da reti neurali utili per il nostro obiettivo finale di classificazione.

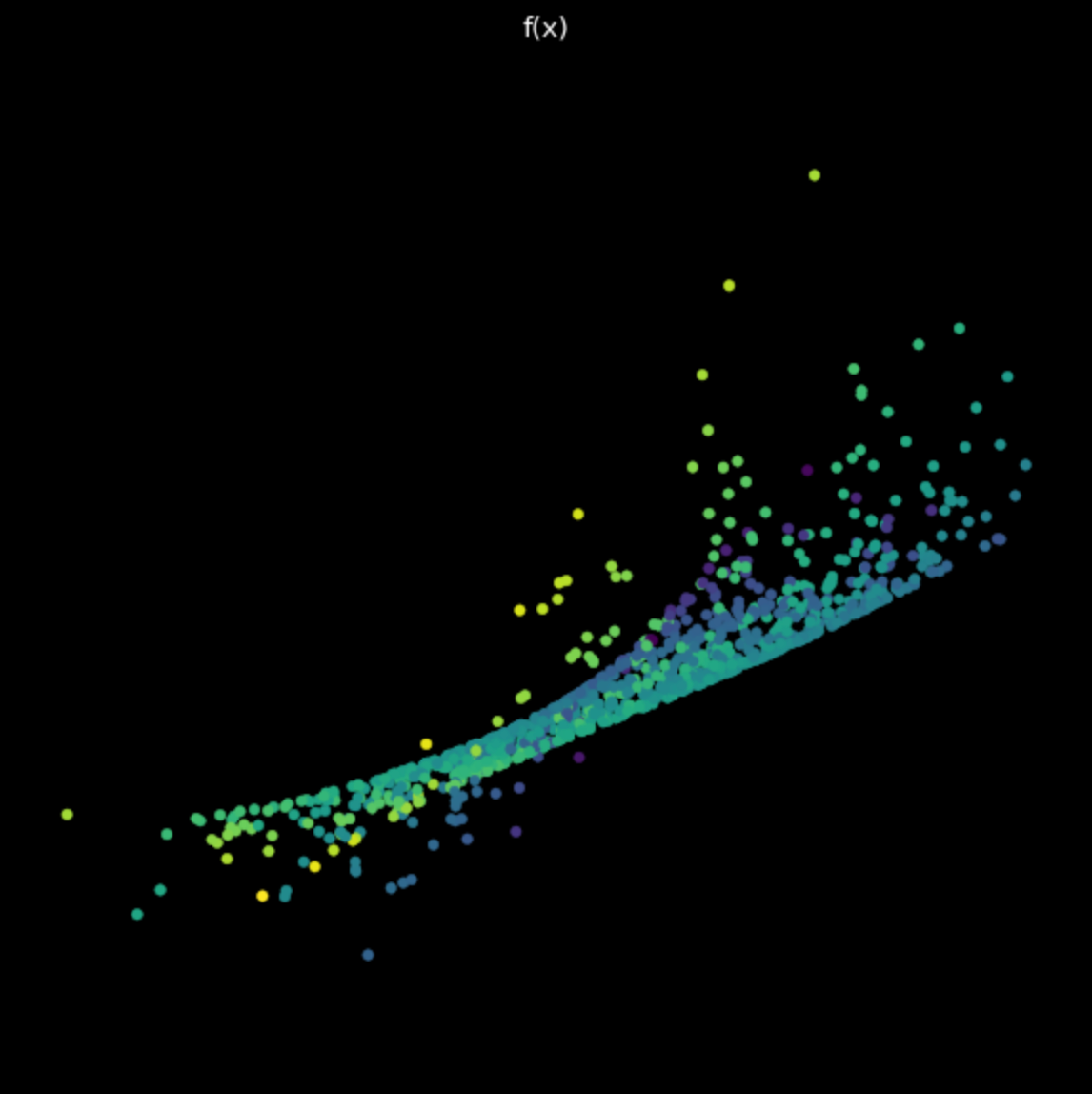
Figura 6: Trasformazione da una rete neurale non addestrata