Overfitting and regularization

Sobreajuste

Considere un problema de regresión. Un modelo podría: ajustarse, encajar bien o sobreajustarse.

Si el modelo no es lo suficientemente expresivo para los datos, se ajustará. Si el modelo es más expresivo que los datos (como es el caso de las redes neuronales profundas), corre el riesgo de sobreajuste.

En este caso, el modelo es lo suficientemente potente como para adaptarse tanto a los datos originales como al ruido, lo que produce una mala solución para la tarea en cuestión.

Idealmente, nos gustaría que nuestro modelo se ajustara a los datos subyacentes y no al ruido, produciendo un buen ajuste para nuestros datos. Nos gustaría especialmente hacer esto sin necesidad de reducir la potencia de nuestros modelos. Los modelos de aprendizaje profundo son muy poderosos, a menudo mucho más de lo estrictamente necesario para aprender los datos. Nos gustaría mantener ese poder (para facilitar el entrenamiento), pero aún así luchar contra el sobreajuste.

Sobreajuste para depuración

El sobreajuste puede resultar útil en algunos casos, como durante la depuración. Se puede probar una red en un pequeño subconjunto de datos de entrenamiento (incluso un solo lote o un conjunto de tensores de ruido aleatorios) y asegurarse de que la red pueda sobreajustarse a estos datos. Si no aprende, es una señal de que puede haber un error.

Regularización

Podemos intentar luchar contra el sobreajuste introduciendo la regularización. La cantidad de regularización afectará el rendimiento de validación del modelo. Muy poca regularización no resolverá el problema de sobreajuste. Demasiada regularización hará que el modelo sea mucho menos efectivo.

• Regularización * agrega conocimientos previos a un modelo; se especifica una distribución previa para los parámetros. Actúa como una restricción sobre el conjunto de posibles funciones aprendibles.

Otra definición de regularización de Ian Goodfellow:

La regularización es cualquier modificación que hacemos a un algoritmo de aprendizaje que tiene como objetivo reducir su error de generalización pero no su error de entrenamiento.

Técnicas de inicialización

Podemos seleccionar un previo para nuestros parámetros de red inicializando los pesos de acuerdo con una distribución particular. Una opción: Xavier initialization.

Regularización de caída de peso

La pérdida de peso es nuestra primera técnica de regularización. La pérdida de peso se usa ampliamente en el aprendizaje automático, pero menos en las redes neuronales. En PyTorch, la caída de peso se proporciona como un parámetro para el optimizador (consulte, por ejemplo, el parámetro weight_decay para SGD).

Esto también se llama:

• L2
• Ridge
• Prior gaussiano

Podemos considerar un objetivo que actúa sobre los parámetros:

entonces tenemos actualizaciones:

Para la disminución de peso, agregamos un término de penalización:

que produce una actualización

Este nuevo término en la actualización lleva los parámetros $\theta$ ligeramente hacia cero, agregando algo de “decaimiento” en los pesos con cada actualización.

Regularización L1

Disponible como una opción para PyTorch optimizers..

También llamado:

• LASSO: Operador selector de contracción mínima absoluta
• Prior laplaciano
• Escasa antes

Al ver esto como una distribución de Laplace anterior, esta regularización pone más masa de probabilidad cerca de cero que una distribución gaussiana.

Comenzando con la misma actualización que la anterior, podemos ver esto como agregar otra penalización:

que produce una actualización

A diferencia del decaimiento de peso de $L_2$, la regularización de $L_1$ “matará” los componentes que están cerca de un eje en el espacio de parámetros, en lugar de reducir uniformemente la longitud del vector de parámetros.

Abandonar

La deserción implica poner a cero una cierta cantidad de neuronas al azar durante el entrenamiento. Esto evita que la red aprenda una ruta singular de entrada a salida. Del mismo modo, debido a la gran parametrización de las redes neuronales, es posible que la red neuronal memorice eficazmente la entrada. Sin embargo, con la deserción, esto es mucho más difícil, ya que la entrada se coloca en una red diferente cada vez, ya que la deserción entrena efectivamente un número infinito de redes que son diferentes cada vez. Por lo tanto, la deserción puede ser una forma poderosa de controlar el sobreajuste y ser más robusto frente a pequeñas variaciones en la entrada.

Figura 1: Red sin abandono

Figura 2: Red con abandono

En PyTorch, podemos establecer una tasa de abandono aleatoria de neuronas.

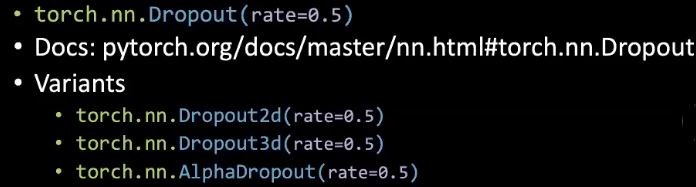
Figura 3: Código de abandono

Después del entrenamiento, durante la inferencia, la deserción ya no se usa. Con el fin de crear la red final para la inferencia, promediamos todas las redes individuales creadas durante el abandono y las usamos para la inferencia. De manera similar, podemos multiplicar todos los pesos por $1/1-p$ donde $p$ es la tasa de abandono.

Parada temprana

Durante el entrenamiento, si la pérdida de validación comienza a aumentar, podemos detener el entrenamiento y usar los mejores pesos encontrados hasta ahora. Esto evita que los pesos crezcan demasiado, lo que comenzará a dañar el rendimiento de la validación en algún momento. En la práctica, es común calcular el rendimiento de la validación en ciertos intervalos y detenerse después de que un cierto número de cálculos de errores de validación dejan de disminuir.

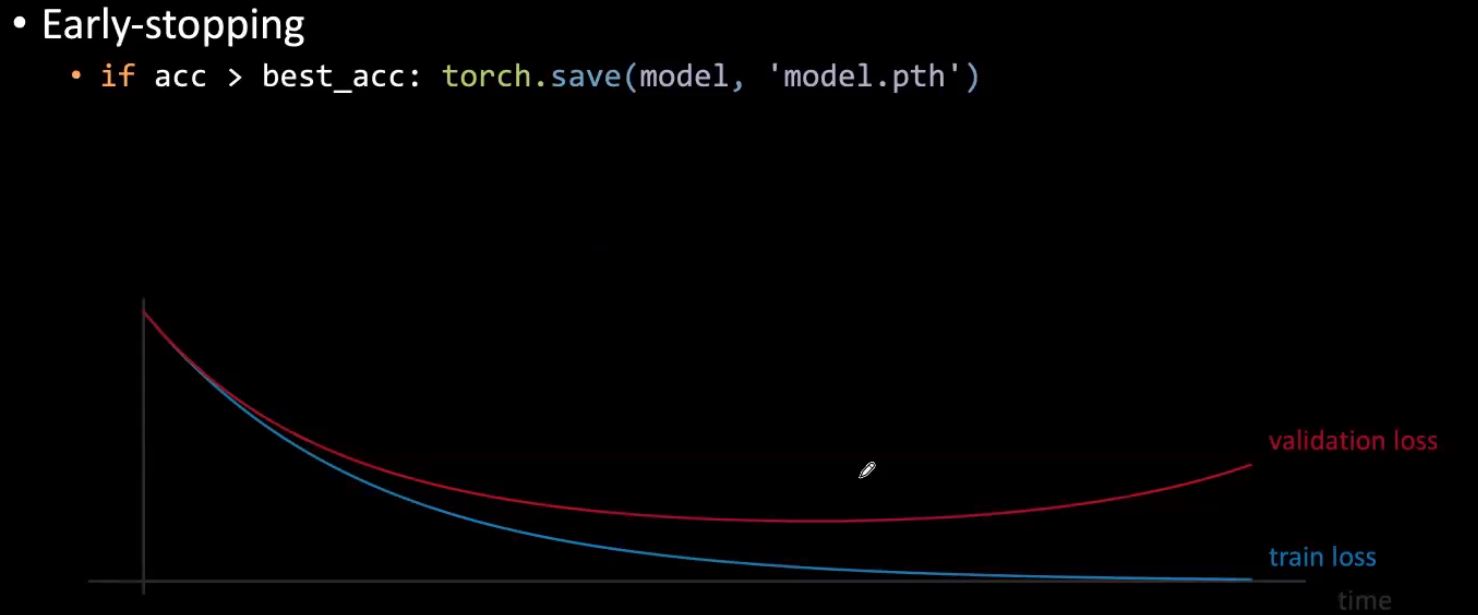
Figura 4: Parada anticipada

Lucha contra el sobreajuste indirecto

Hay técnicas que tienen el efecto secundario de regularizar parámetros pero no son regularizadores en sí mismos.

Norma de lote

P. ¿Cómo la norma por lotes hace que la capacitación sea más eficiente? R. Podemos utilizar una tasa de aprendizaje más alta al aplicar la norma por lotes.

La normalización por lotes se utiliza para evitar el cambio de covariables interno de una red neuronal, pero existe un gran debate sobre si realmente hace esto y cuál es el verdadero beneficio.

Figura 5: Normalización por lotes

La normalización por lotes esencialmente extiende la lógica de normalizar la entrada de la red neuronal para normalizar la entrada de cada capa oculta en la red. La idea básica es tener una distribución fija que alimente cada capa subsiguiente de una red neuronal, ya que el aprendizaje ocurre mejor cuando tenemos una distribución fija. Para hacer esto, calculamos la media y la varianza de cada lote antes de cada capa oculta y normalizamos los valores entrantes mediante estas estadísticas específicas del lote, lo que reduce la cantidad en la que los valores finalmente cambiarán durante el entrenamiento.

Con respecto al efecto de regularización, debido a que cada lote es diferente, cada muestra se normalizará con estadísticas ligeramente diferentes basadas en el lote en el que se encuentra. Por lo tanto, la red verá varias versiones ligeramente alteradas de una sola entrada que ayuda a la red a aprender a ser más robusto frente a ligeras variaciones en la entrada y evita el sobreajuste.

Otro beneficio de la normalización por lotes es que el entrenamiento es mucho más rápido.

Más datos

Recopilar más datos es una forma fácil de evitar el sobreajuste, pero puede resultar caro o no factible.

Aumento de datos

Las transformaciones que utilizan Torchvision pueden tener un efecto de regularización al enseñar a la red a aprender a ser insensible a las perturbaciones.

Figure 6: Data augmentation with Torchvision.

Ajuste fino de inclinación de transferencia (TF) (FT)

El aprendizaje por transferencia (TF) se refiere simplemente a entrenar a un clasificador final en la parte superior de una red previamente entrenada (generalmente se usa en casos de pocos datos).

El ajuste fino (FT) también se refiere al entrenamiento de porciones parciales / completas del netowrk previamente entrenado (utilizado en los casos en los que tenemos muchos datos en general).

P. Generalmente, ¿cuándo deberíamos congelar las capas de un modelo previamente entrenado? R. Si tenemos pocos datos de entrenamiento.

4 casos generales: 1) Si tenemos pocos datos con distribuciones similares, podemos simplemente transferir el aprendizaje. 2) Si tenemos muchos datos con distribuciones similares, podemos hacer ajustes para mejorar también el rendimiento del extractor de características. 3) Si tenemos pocos datos y una distribución diferente, deberíamos eliminar algunas de las capas finales entrenadas en el extractor de características, ya que son demasiado especializadas. 4) Si tenemos muchos datos y son de diferentes distribuciones, podemos entrenar todas las porciones.

Tenga en cuenta que también podemos usar diferentes tasas de aprendizaje para diferentes capas a fin de mejorar el rendimiento.

Para ampliar nuestra discusión sobre el sobreajuste y la regularización, veamos las visualizaciones a continuación. Estas visualizaciones se generaron con el código de Notebook.

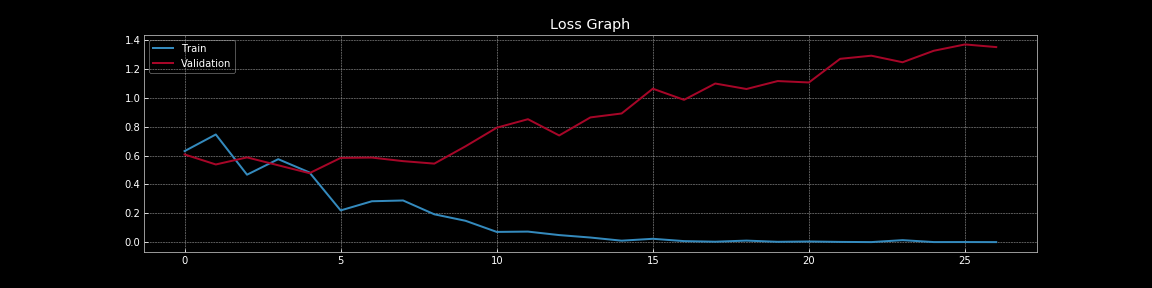
Figure 7: Curvas de pérdida sin abandono

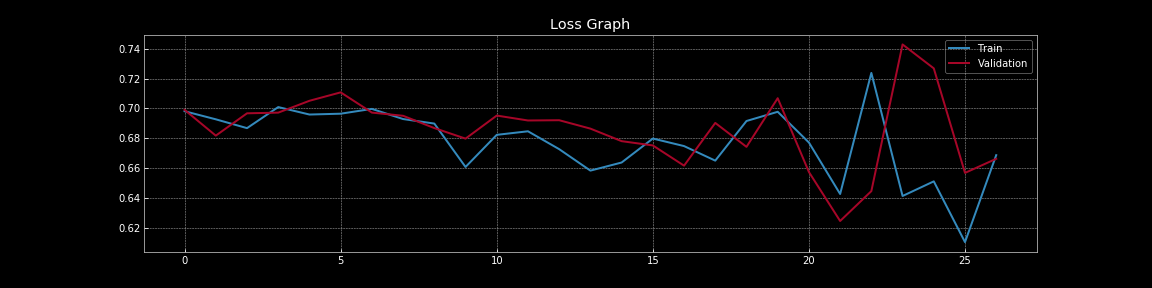
Figure 8: Curvas de pérdida con deserción

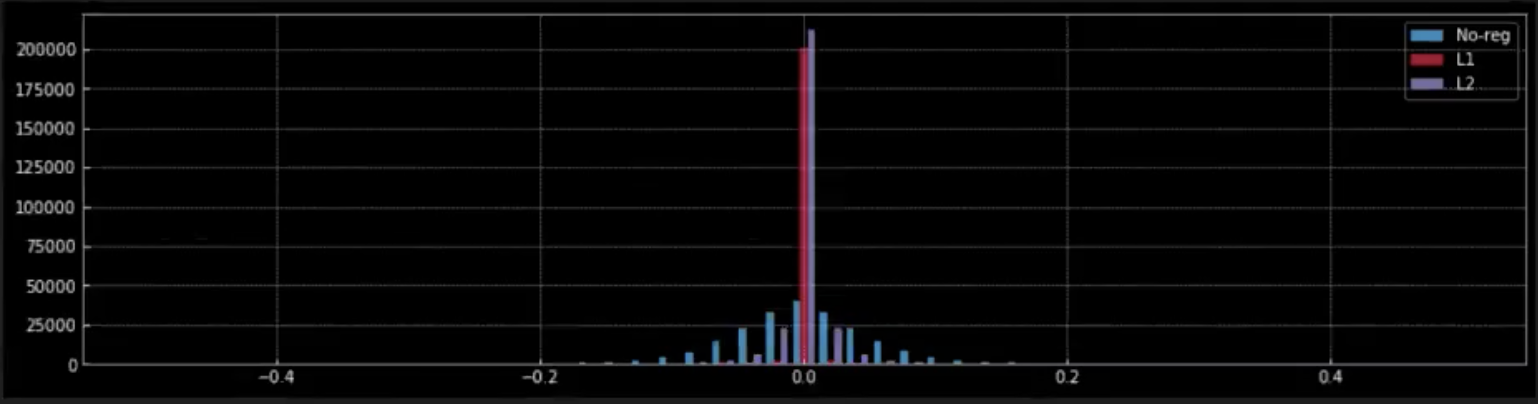
Figure 9: Efecto de la regularización sobre los pesos

De la Figura 7 y la Figura 8, podemos comprender el efecto dramático que tiene la deserción en el error de generalización, es decir, la diferencia entre la pérdida de entrenamiento y la pérdida de validación. En la Figura 7, sin abandonos hay un claro sobreajuste ya que la pérdida de entrenamiento es mucho menor que la pérdida de validación.

Sin embargo, en la Figura 8, con el abandono, la pérdida de entrenamiento y la pérdida de validación se superponen casi continuamente, lo que indica que el modelo se está generalizando bien al conjunto de validación, que sirve como nuestro proxy para el conjunto fuera de la muestra. Por supuesto, podemos medir el rendimiento real fuera de la muestra utilizando un conjunto de pruebas de exclusión por separado.

En la Figura 9, observamos el efecto que tiene la regularización (L1 y L2) sobre los pesos de la red.

• Cuando aplicamos la regularización L1, desde el pico rojo en cero, podemos entender que la mayoría de los pesos son cero. Los pequeños puntos rojos más cercanos a cero son los pesos distintos de cero del modelo.

• Por el contrario, en la regularización L2, desde el pico azul cercano a cero podemos ver que la mayoría de los pesos están cerca de cero pero distintos de cero.

• Cuando no hay regularización (lavanda) los pesos son mucho más flexibles y se distribuyen alrededor de cero pareciendo una distribución normal.

Redes neuronales bayesianas: estimación de la incertidumbre en torno a las predicciones

Nos preocupamos por la incertidumbre en las redes neuronales porque una red necesita saber qué tan segura / segura de su predicción.

Por ejemplo: si construye una red neuronal para predecir el control de dirección, necesita saber qué tan confiables son las predicciones de la red.

Podemos usar una red neuronal con abandono para obtener un intervalo de confianza alrededor de nuestras predicciones. Entrenemos una red con deserción, siendo $r$ la tasa de deserción.

Por lo general, durante la inferencia, configuramos la red en modo de validación y usamos todas las neuronas para obtener la predicción final. Mientras hacemos la predicción, escalamos los pesos $\delta$ por $\dfrac {1} {1-r}$ para tener en cuenta la caída de neuronas durante el entrenamiento.

Este método nos da una única predicción para cada entrada. Sin embargo, para obtener un intervalo de confianza alrededor de nuestra predicción, necesitamos múltiples predicciones para la misma entrada. Entonces, en lugar de configurar la red en modo de validación durante la inferencia, la retenemos en modo de entrenamiento es decir, todavía suelta neuronas al azar y obtenemos una predicción. Cuando predecimos varias veces usando esta red de deserción, para la misma entrada obtendremos diferentes predicciones dependiendo de las neuronas que se eliminen. Usamos estas predicciones para estimar la predicción final promedio y un intervalo de confianza a su alrededor.

En las siguientes imágenes, hemos estimado intervalos de confianza en torno a las predicciones de redes. Estas visualizaciones se generaron con el código de Bayesian Neural Networks Notebook. La línea roja representa las predicciones. La región sombreada de color púrpura alrededor de las predicciones representa la incertidumbre es decir, la varianza de las predicciones.

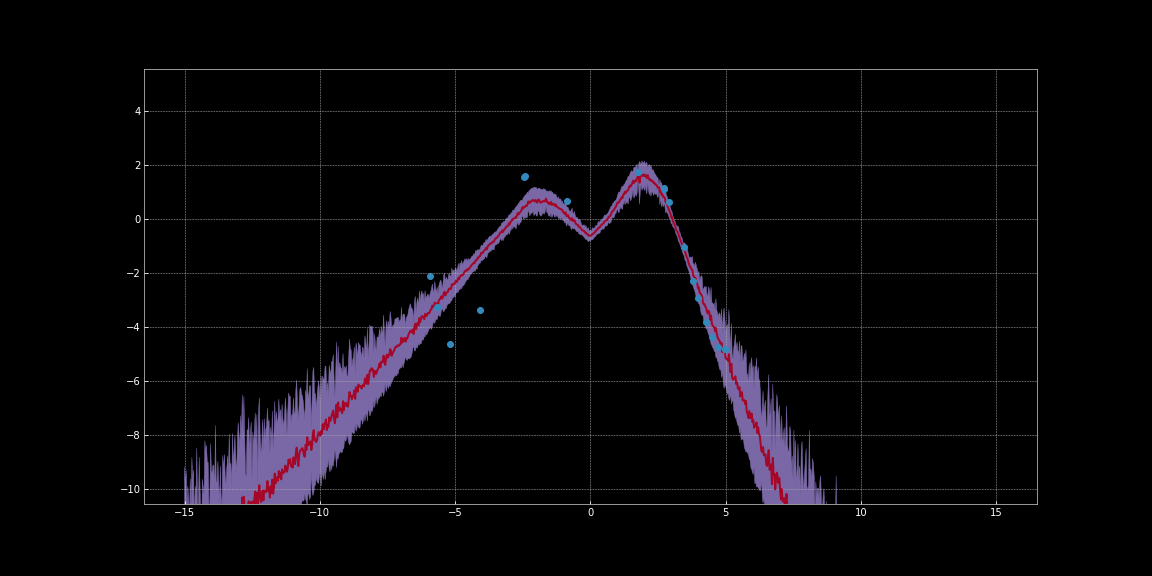
Figure 10: Estimación de la incertidumbre mediante la activación de ReLU

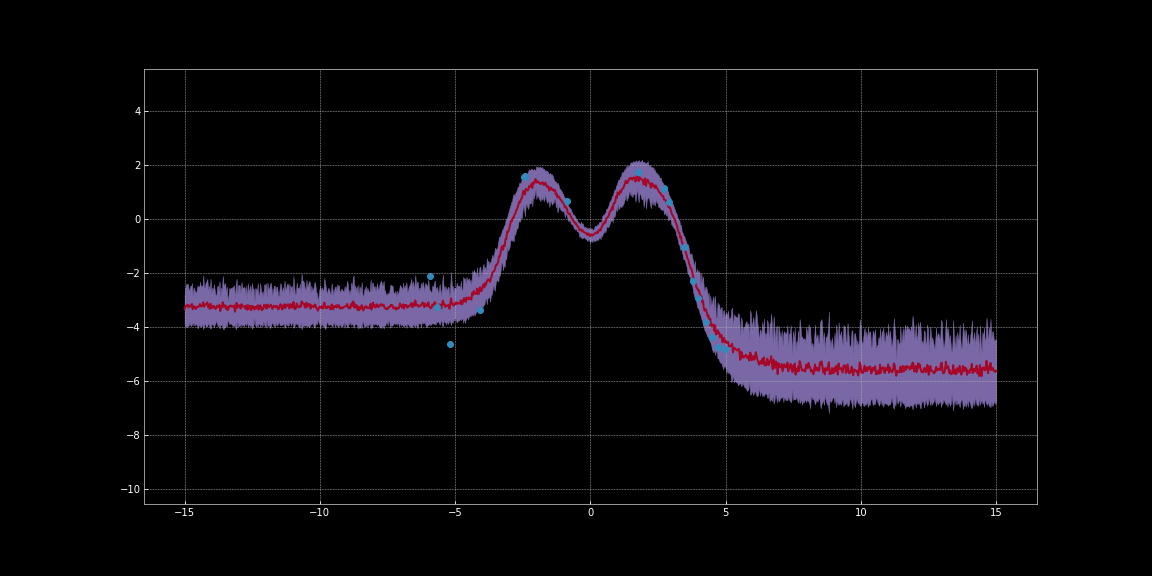
Figure 11: Estimación de la incertidumbre mediante la activación de Tanh

Como puede observar en las imágenes anteriores, estas estimaciones de incertidumbre no están calibradas. Son diferentes para diferentes funciones de activación. Notablemente en las imágenes, la incertidumbre en torno a los puntos de datos es baja. Además, la varianza que podemos observar es una función diferenciable. Entonces podemos ejecutar un descenso de gradiente para minimizar esta variación. De este modo podemos obtener predicciones más seguras.

Si tenemos varios términos que contribuyen a la pérdida total en nuestro modelo de EBM, ¿cómo interactúan?

En los modelos EBM, podemos sumar de manera simple y conveniente los diferentes términos para estimar la pérdida total.

Digresión: un término que penaliza la longitud de la variable latente puede actuar como uno de los muchos términos de pérdida en un modelo. La longitud de un vector es aproximadamente proporcional al número de dimensiones que tiene. Entonces, si disminuye el número de dimensiones, la longitud del vector disminuye y, como resultado, codifica menos información. En una configuración de codificador automático, esto asegura que el modelo está reteniendo la información más importante. Entonces, una forma de bloquear la información en los espacios latentes es reducir la dimensionalidad del espacio latente.

¿Cómo podemos determinar el hiperparámetro para regularización?

En la práctica, para determinar el hiperparámetro óptimo para la regularización, es decir, la fuerza de regularización, podemos usar

• Optimización de hiperparámetros bayesianos
• Búsqueda de cuadrícula
• Búsqueda aleatoria

Al hacer estas búsquedas, las primeras épocas suelen ser suficientes para darnos una idea de cómo está funcionando la regularización. Entonces necesitamos train el modelo extensamente.