Graphical Energy-based Methods
$$\gdef \sam #1 {\mathrm{softargmax}(#1)}$$
$$\gdef \vect #1 {\boldsymbol{#1}} $$
$$\gdef \matr #1 {\boldsymbol{#1}} $$
$$\gdef \E {\mathbb{E}} $$
$$\gdef \V {\mathbb{V}} $$
$$\gdef \R {\mathbb{R}} $$
$$\gdef \N {\mathbb{N}} $$
$$\gdef \relu #1 {\texttt{ReLU}(#1)} $$
$$\gdef \D {\,\mathrm{d}} $$
$$\gdef \deriv #1 #2 {\frac{\D #1}{\D #2}}$$
$$\gdef \pd #1 #2 {\frac{\partial #1}{\partial #2}}$$
$$\gdef \set #1 {\left\lbrace #1 \right\rbrace} $$
% My colours
$$\gdef \aqua #1 {\textcolor{8dd3c7}{#1}} $$
$$\gdef \yellow #1 {\textcolor{ffffb3}{#1}} $$
$$\gdef \lavender #1 {\textcolor{bebada}{#1}} $$
$$\gdef \red #1 {\textcolor{fb8072}{#1}} $$
$$\gdef \blue #1 {\textcolor{80b1d3}{#1}} $$
$$\gdef \orange #1 {\textcolor{fdb462}{#1}} $$
$$\gdef \green #1 {\textcolor{b3de69}{#1}} $$
$$\gdef \pink #1 {\textcolor{fccde5}{#1}} $$
$$\gdef \vgrey #1 {\textcolor{d9d9d9}{#1}} $$
$$\gdef \violet #1 {\textcolor{bc80bd}{#1}} $$
$$\gdef \unka #1 {\textcolor{ccebc5}{#1}} $$
$$\gdef \unkb #1 {\textcolor{ffed6f}{#1}} $$
% Vectors
$$\gdef \vx {\pink{\vect{x }}} $$
$$\gdef \vy {\blue{\vect{y }}} $$
$$\gdef \vb {\vect{b}} $$
$$\gdef \vz {\orange{\vect{z }}} $$
$$\gdef \vtheta {\vect{\theta }} $$
$$\gdef \vh {\green{\vect{h }}} $$
$$\gdef \vq {\aqua{\vect{q }}} $$
$$\gdef \vk {\yellow{\vect{k }}} $$
$$\gdef \vv {\green{\vect{v }}} $$
$$\gdef \vytilde {\violet{\tilde{\vect{y}}}} $$
$$\gdef \vyhat {\red{\hat{\vect{y}}}} $$
$$\gdef \vycheck {\blue{\check{\vect{y}}}} $$
$$\gdef \vzcheck {\blue{\check{\vect{z}}}} $$
$$\gdef \vztilde {\green{\tilde{\vect{z}}}} $$
$$\gdef \vmu {\green{\vect{\mu}}} $$
$$\gdef \vu {\orange{\vect{u}}} $$
% Matrices
$$\gdef \mW {\matr{W}} $$
$$\gdef \mA {\matr{A}} $$
$$\gdef \mX {\pink{\matr{X}}} $$
$$\gdef \mY {\blue{\matr{Y}}} $$
$$\gdef \mQ {\aqua{\matr{Q }}} $$
$$\gdef \mK {\yellow{\matr{K }}} $$
$$\gdef \mV {\lavender{\matr{V }}} $$
$$\gdef \mH {\green{\matr{H }}} $$
% Coloured math
$$\gdef \cx {\pink{x}} $$
$$\gdef \ctheta {\orange{\theta}} $$
$$\gdef \cz {\orange{z}} $$
$$\gdef \Enc {\lavender{\text{Enc}}} $$
$$\gdef \Dec {\aqua{\text{Dec}}}$$
🎙️
Yann LeCun
Comparación de pérdidas
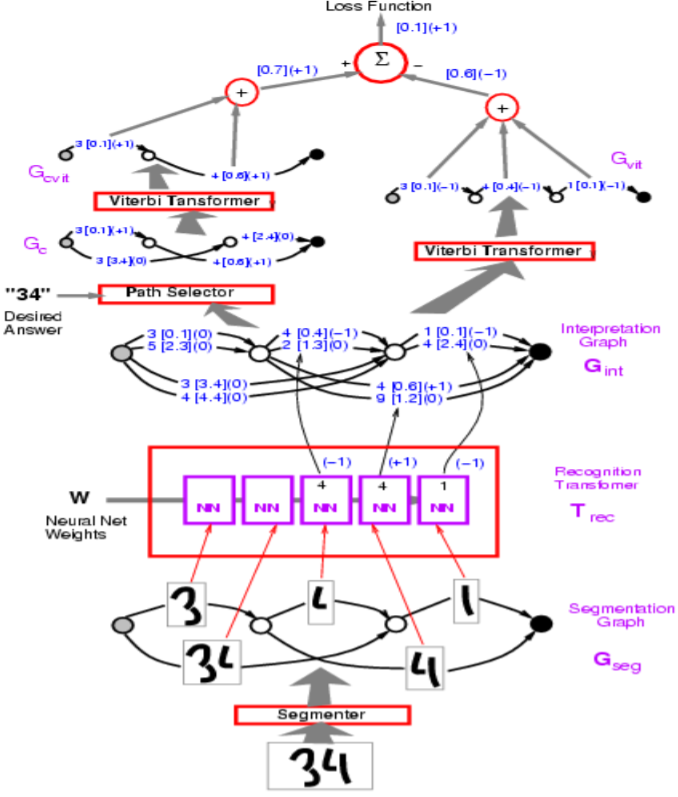
Figura 1: Arcitectura de la red
En la figura anterior, las rutas incorrectas tienen -1.
El profesor LeCun comienza con la pérdida de perceptrón, que se utiliza en el ejemplo de Graph Transformer Model en la figura anterior. El objetivo es aumentar la energía de las respuestas incorrectas y reducir las respuestas correctas.
En términos de implementación, representaría los arcos en la visualización con un vector. En lugar de un arco separado para cada categoría, un vector contiene tanto las categorías como la puntuación para cada categoría.
P: ¿Cómo se implementa el segmento o en el modelo anterior?
R: El segmento es heurístico artesanal. El modelo utiliza un segmento artesanal aunque hay una forma de hacerlo entrenable de principio a fin. Este enfoque artesanal fue reemplazado por el enfoque de ventana deslizante para el reconocimiento de personajes.
Resumen de las funciones de pérdida
Tabla 1: Varias ecuaciones de pérdida
| Ecuacion de pérdida |
Formula |
Margen |
| Perdida de energia |
$\text{E}(\text{W}, \text{Y}^i, \text{X}^i)$ |
None |
| Perceptron |
$\text{E}(\text{W}, \text{Y}^i, \text{X}^i)-\min\limits_{\text{Y}\in\mathcal{Y}}\text{E}(\text{W}, \text{Y}, \text{X}^i)$ |
0 |
| Bisagra |
$\max\big(0, m + \text{E}(\text{W}, \text{Y}^i,\text{X}^i)-\text{E}(\text{W}, \overline{\text{Y}}^i,\text{X}^i)\big)$ |
$m$ |
| Log |
$\log\bigg(1+\exp\big(\text{E}(\text{W}, \text{Y}^i,\text{X}^i)-\text{E}(\text{W}, \overline{\text{Y}}^i,\text{X}^i)\big)\bigg)$ |
>0 |
| LVQ2 |
$\min\bigg(M, \max\big(0, \text{E}(\text{W}, \text{Y}^i,\text{X}^i)-\text{E}(\text{W}, \overline{\text{Y}}^i,\text{X}^i)\big)\bigg)$ |
0 |
| MCE |
$\bigg(1+\exp\Big(-\big(\text{E}(\text{W}, \text{Y}^i,\text{X}^i)-\text{E}(\text{W}, \overline{\text{Y}}^i,\text{X}^i)\big)\Big)\bigg)^{-1}$ |
>0 |
| Cuadrado-cuadrado |
$\text{E}(\text{W}, \text{Y}^i,\text{X}^i)^2-\bigg(\max\big(0, m - \text{E}(\text{W}, \overline{\text{Y}}^i,\text{X}^i)\big)\bigg)^2$ |
$m$ |
| Cuadrado-Exp |
$\text{E}(\text{W}, \text{Y}^i,\text{X}^i)^2 + \beta\exp\big(-\text{E}(\text{W}, \overline{\text{Y}}^i,\text{X}^i)\big)$ |
>0 |
| NNL/MMI |
$\text{E}(\text{W}, \text{Y}^i,\text{X}^i) + \frac{1}{\beta}\log\int_{y\in\mathcal{Y}}\exp\big(-\beta\text{E}(\text{W}, y,\text{X}^i)\big)$ |
>0 |
| MEE |
$1-\frac{\exp\big(-\beta E(W,Y^i,X^i)\big)}{\int_{y\in\mathcal{Y}}\exp\big(-\beta E(W,y,X^i)\big)}$ |
>0 |
La pérdida de perceptrón que se ve en la tabla anterior no tiene margen y, por lo tanto, la pérdida tiene el riesgo de colapsar.
- La «pérdida de bisagra» consiste en tomar la energía de la peor respuesta y la respuesta correcta y calcular su diferencia. Intuitivamente, con un margen ‘m’, la bisagra solo tendrá una pérdida de 0 cuando la energía correcta sea menor que la energía más ofensiva en (al menos) ‘m’.
- La pérdida de MCE se utiliza en el reconocimiento de voz y se parece a un sigmoide.
- La pérdida de NLL tiene como objetivo hacer que la energía de la respuesta correcta sea pequeña y que el componente logarítmico de la ecuación sea grande.
P: ¿Cómo puede ser mejor la bisagra que la pérdida NLL?
R: Bisagra es mejor que NLL porque NLL intentará llevar la diferencia entre la respuesta correcta y otras respuestas al infinito, mientras que Hinge solo quiere que sea más grande que algún valor (el margen m).
DEFINICIÓN:
Un decodificador ltoma como variable de entrada una secuencia de vectores que indican las puntuaciones o la energía de sonidos o imágenes individuales y selecciona la mejor salida posible.
P: ¿Cuáles son algunos ejemplos de problemas que se pueden utilizar con decodificadores?
R: Modelado de idiomas, traducción automática y etiquetado de secuencias.
Composición de grafos
La composición de grafos nos permite combinar dos grafos. En este ejemplo, podemos ver un léxico de un modelo de lenguaje representado como $trie$ (un grafo) y un grafo de reconocimiento producido por una red neuronal.
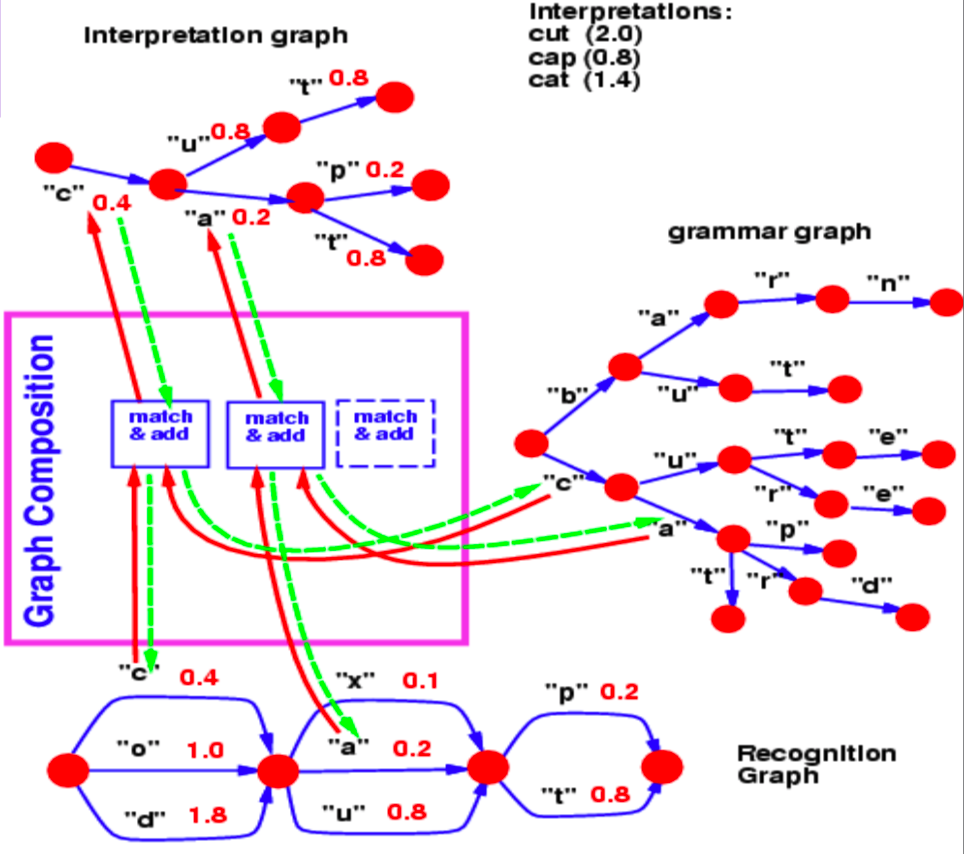
Figura 2: Composicion del grafo
El grafo de reconocimiento especifica con diferentes valores de energía (asociados con cada arco) la probabilidad de que un personaje esté en un paso en particular.
Ahora, para este ejemplo, la pregunta que respondemos con una operación de composición de grafo es, ¿cuál es el mejor camino en este grafo de reconocimiento que también concuerda con nuestro léxico?
El salto común del paso 1 al paso 2 entre el grafo de reconocimiento y la gramática es el carácter $ c$, asociado con la energía 0.4. Por lo tanto, nuestro grafo de interpretación contiene solo 1 arco entre el paso 1 y 2 correspondiente a $c$. De manera similar, los caracteres posibles entre los pasos 2 y 3 son $ x$, $u$ y $ a$ en el gráfico de reconocimiento. Las ramas que siguen a $ c$ en el gráfico gramatical contienen $ u$ y $ a$. Entonces, la operación de composición de grafos selecciona los arcos $ u$ y $a$ para que estén presentes en el grafo de interpretación. También asocia el arco que copia del grafo de reconocimiento con sus valores de energía.
Si la gramática también contuviese valores de energía asociados con arcos, la composición del grafo habría agregado los valores de energía o los habría combinado usando algún otro operador.
De manera similar, la composición de grafos también nos permite combinar dos bases de conocimiento que están representadas por redes neuronales. En el ejemplo discutido anteriormente, la gramática se puede representar esencialmente como una red neuronal que predice el siguiente carácter. La salida softmax del NN nos proporciona las probabilidades de transición al siguiente carácter de un nodo dado.
Como nota al margen, si el modelo de lenguaje que se muestra en este ejemplo es una red neuronal, podemos propagar hacia atrás a través de toda la estructura. Esto se convierte en un ejemplo de un programa diferenciable en el que retropropagamos a través de un programa que contiene bucles, condiciones if, recursiones, etc.
Toda la arquitectura de un lector de cheques de mediados de los 90 es bastante compleja, pero lo que más nos interesa es la parte que parte del reconocedor de caracteres, que produce el gráfico de reconocimiento.

Figura 3 : lector de cheques
</center>
Este gráfico de reconocimiento se somete a dos operaciones de composición separadas, una con la interpretación correcta (o la verdad básica) y la segunda con la gramática que crea un gráfico de todas las posibles interpretaciones.
Todo el sistema se entrena mediante la función de pérdida de probabilidad logarítmica negativa. La probabilidad logarítmica negativa dice que cada camino en el grafo de interpretación es una posible interpretación y la suma de energías a lo largo de ese camino es la energía de esa interpretación.
Ahora, en lugar de usar el algoritmo de Viterbi, usamos el algoritmo de avance. Las siguientes subsecciones discuten las diferencias entre los dos enfoques.
#### Algoritmo de Viterbi
El algoritmo de Viterbi es un algoritmo de programación dinámica que se utiliza para encontrar la ruta más probable (o la ruta con la energía mínima) en un gráfico dado. Minimiza la energía con respecto a una variable latente z, donde z representa el camino que estamos tomando en la gráfica.
$$ F (x, y) = \min_ {z} \; E (x, y, z) $$
#### El algoritmo de avance
El algoritmo directo, por otro lado, calcula el logaritmo de la suma de exponenciales del valor negativo de las energías de todos los caminos. Esto se puede ver fácilmente como una fórmula a continuación:
$$F_{\beta} (x, y) = -\frac{1}{\beta} \; \log \; \sum_{z \, \in \, \text{paths}} \; \exp \, (- \beta \; E(x, y, z))$$
Esto es marginalizar sobre la variable latente z, que define las rutas en un grafo de interpretación. Este enfoque calcula este valor exponencial de suma logarítmica en todas las rutas posibles a un nodo en particular. Esto es como combinar el costo de todos los caminos posibles de una manera mínima suave.
El algoritmo de reenvío es barato de implementar y no cuesta más que el algoritmo de Viterbi. Además, podemos propagar hacia atrás a través del nodo del algoritmo de avance en el gráfico.
El funcionamiento del algoritmo de avance se puede mostrar utilizando el siguiente ejemplo definido en un gráfico de interpretación.

Figura 4 : Gráfico de interpretación
</center>
El costo desde el nodo de entrada hasta el nodo sombreado en rojo se calcula marginando todos los caminos posibles que llegan al nodo rojo. Las flechas que entran en el nodo rojo definen estas posibles rutas en nuestro ejemplo.
Para el nodo rojo, el valor de la energía en el nodo viene dado por:
$$-\frac{1}{\beta} \; \log \; [ \, \exp \, (- \, \beta (e_1 \, + \, e_3)) \; + \; \exp \, (- \, \beta (e_2 \, + \, e_4)) \, ]$$
#### Analogía de red neuronal del algoritmo directo
El algoritmo de avance es un caso especial del algoritmo de propagación de creencias, cuando el grafo subyacente es un grafo de cadena. Todo este algoritmo puede verse como una red neuronal de retroalimentación donde la función en cada nodo es una suma logarítmica de exponenciales y un término de suma.
Para cada nodo en el gráfico de interpretación, mantenemos una variable $\alpha$.
$$ \alpha_{i} = - \; \log \; \biggl[ \sum_{k \, \in \, \text{parent} \, (i)} \; \exp \, (- \, \beta \; (\alpha_k \, + \, e_{ki})) \biggl]$$
donde $ e_ {ki} $ es la energía del enlace desde el nodo $ k $ al nodo $i$.
$\alpha_i$ forma la activación de un nodo $i$ en esta red neuronal y $e_ {ki}$ es el peso entre los nodos $k$ y el nodo $i$. Esta formulación es algebraicamente equivalente a las operaciones de suma ponderada de una red neuronal regular en el dominio logarítmico.
Podemos retropropagar a través del gráfico de interpretación dinámica (ya que cambia de un ejemplo a otro) en el que aplicamos el algoritmo de avance. Podemos calcular los gradientes de $F (x, y)$ calculados en el último nodo del grafo con los pesos $e_ {ki}$ que definen los bordes del gráfico de interpretación.
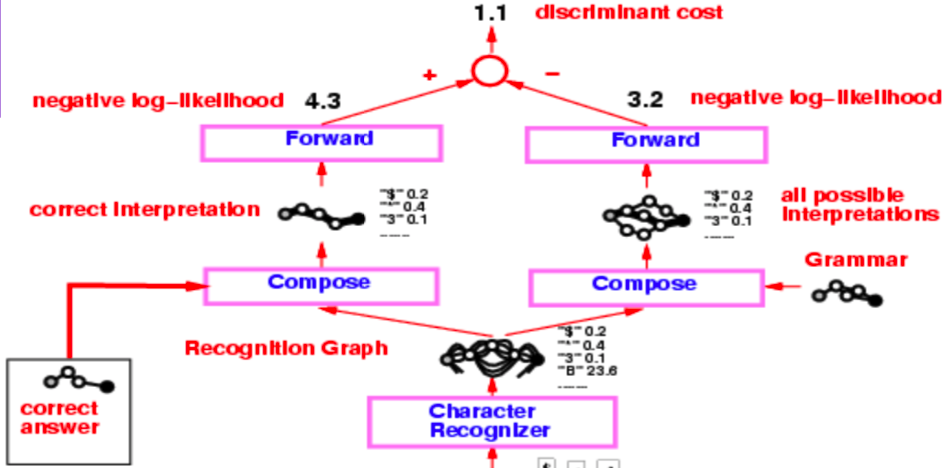
Figure 5: Check reader
Volviendo al ejemplo del lector de cheques, aplicamos el algoritmo de avance en las dos composiciones de grafos y obtenemos el valor de energía en el último nodo utilizando el foro exponencial de suma logarítmica. La diferencia entre estos valores de energía es la pérdida de probabilidad logarítmica negativa.
El valor obtenido al aplicar el algoritmo de avance en la composición del gráfico entre la respuesta correcta y el gráfico de reconocimiento es el valor exponencial de la suma logarítmica de la respuesta correcta. Por el contrario, el valor exponencial de la suma logarítmica en el último nodo de la composición del gráfico entre el gráfico de reconocimiento y la gramática es el valor marginado sobre todas las posibles interpretaciones válidas.
# Formulación Lagrangiana de retropropagación
Para una entrada $x$ y una salida objetivo $y$, podemos formular una red como una colección de funciones, $f_k$ y pesos, $w_k$ de manera que los pasos sucesivos en la red generen $z_k$ con $z_ {k + 1} = f_k (z_k, w_k)$. En un entorno supervisado, el objetivo de la red es minimizar $C (z_n, y)$, el costo de la salida $n ^ \mathrm {th}$ de la red, con respecto a la verdad del terreno. Esto es equivalente al problema de minimizar $C (z_n, y)$ con respecto a las restricciones $z_ {k + 1} = f_k (z_k, w_k)$ y $z_0 = x$.
El lagrangiano se puede escribir:
$$ \mathcal {L} (x, y, \lambda_i, z_i, w_i) = C (z_n, y) + \sum \limits_ {k = 0} ^ {n-1} \lambda ^ T_ {k + 1 } (z_ {k + 1} - f_k (z_k, w_k)) $$
donde los términos $\lambda$ denotan multiplicadores de Lagrange (ver [Paul's online notes](http://tutorial.math.lamar.edu/Classes/CalcIII/LagrangeMultipliers.aspx) para un repaso si Calc 3 fue tomada hace un tiempo).
Para minimizar $\mathcal {L}$, necesitamos establecer las derivadas parciales de $\ mathcal{L}$ con respecto a cada uno de sus argumentos a cero y resolver.
- Para $\lambda$, simplemente recuperamos la restricción: $\frac{\partial{\mathcal{L}}}{\partial \lambda_{k+1}} = 0 \rightarrow z_{k+1} = f_k(z_k, w_k)$.
-
- Para $z_k$, $\frac{\partial \mathcal{L}}{\partial z_k} = 0 \rightarrow \lambda^T_k - \lambda^T_{k+1} \frac{\partial f_k(z_k, w)}{\partial z_k} \rightarrow \lambda_k = \frac{\partial f_k(z_k, w_k)^T}{\partial z_k}\lambda_{k+1}$, que es solo la fórmula de retropropagación estándar.
Este enfoque se originó con Lagrange y Hamilton en el contexto de la Mecánica Clásica, donde la minimización está sobre la energía del sistema y los términos $\lambda$ denotan restricciones físicas del sistema, como dos bolas que se ven obligadas a permanecer a una distancia fija. unos de otros en virtud de estar unidos por una barra de metal, por ejemplo.
En una situación en la que necesitamos minimizar el costo $C$ en cada paso de tiempo, $k$, el Lagrangiano se convierte en
$$ \mathcal{L} = \sum_k \left(C_k(z_k, y_k) + \lambda^T_{k+1}(z_{k+1} - f_k(z_k, w_k)) \right) $$.
# Ecuación diferencial ordinaria neural (ODE)
Usando esta formulación de retropropagación, ahora podemos hablar de una nueva clase de modelos, Neural ODEs (Ecuacion Diferencial Ordinaria). Estas son básicamente redes recurrentes donde el estado, $z$, en el momento $ t $ viene dado por $ z_{t+\text{d}t} = z_t + f(z_t, W) dt$, donde $ W $ representa un conjunto de parámetros fijos.
Esto también se puede expresar como una ecuación diferencial ordinaria (sin derivadas parciales): $\frac{\text{d}z}{\text{d}t} = f(z_t, W)$.
Entrenar una red de este tipo utilizando la formulación lagrangiana es muy sencillo. Si tenemos un objetivo, $y$, y queremos que el estado del sistema alcance $y$ en el tiempo $T$, simplemente establecemos la función de costo como la distancia entre $z_T$ y $ y $. Otro objetivo de la red podría ser encontrar un estado estable del sistema, es decir, uno que deje de cambiar después de cierto punto.
Matemáticamente, esto es equivalente a establecer $\frac{\text{d}z}{\text{d}t} = f(y, W) = 0$. En general, encontrar una solución, $y$ para esta ecuación es mucho más fácil que la propagación hacia atrás en el tiempo, porque la red no necesita recordar el gradiente con respecto a toda la secuencia, y solo tiene que minimizar $f$ o $ \lvert f \rvert ^ 2$. Para obtener más información sobre el entrenamiento de ODE neuronales para alcanzar puntos fijos, consulte [(Lecun88)](http://yann.lecun.com/exdb/publis/pdf/lecun-88.pdf).
# Inferencia variacional en términos de energía
## Introducción
Para una función de energía elemental $E (x, y, z)$, si deseamos marginar sobre una variable, z, para obtener una pérdida en términos de solo $x$ y $y$, $L (x, y)$, debemos calcular
$$L(x,y) = -\frac{1}{\beta}\int_z \exp(-\beta E(x,y,z))$$
Si luego multiplicamos por $\frac {q (z)} {q (z)}$, obtenemos
$$L(x,y) = -\frac{1}{\beta}\int_z q(z) \frac{\exp({-\beta E(x,y,z)})}{q(z)}$$
Si asumimos que $q (z)$ es una distribución de probabilidad sobre $z$, podemos interpretar nuestra integral de función de pérdida reescrita como un valor esperado, con respecto a la distribución de $\frac{\exp({-\beta E(x,y,z)})}{q(z)}$.
Usamos esta interpretación, la Desigualdad de Jensen y las aproximaciones basadas en muestreo, para optimizar indirectamente nuestra función de pérdida.
## Desigualdad de Jensen
La desigualdad de Jensen es una observación geométrica que establece: si tenemos una función convexa, entonces la *expectativa* de esa función, en un rango, es menor que el promedio de la función evaluada al principio y al final del rango. Ilustrado geométricamente, esto es muy intuitivo:
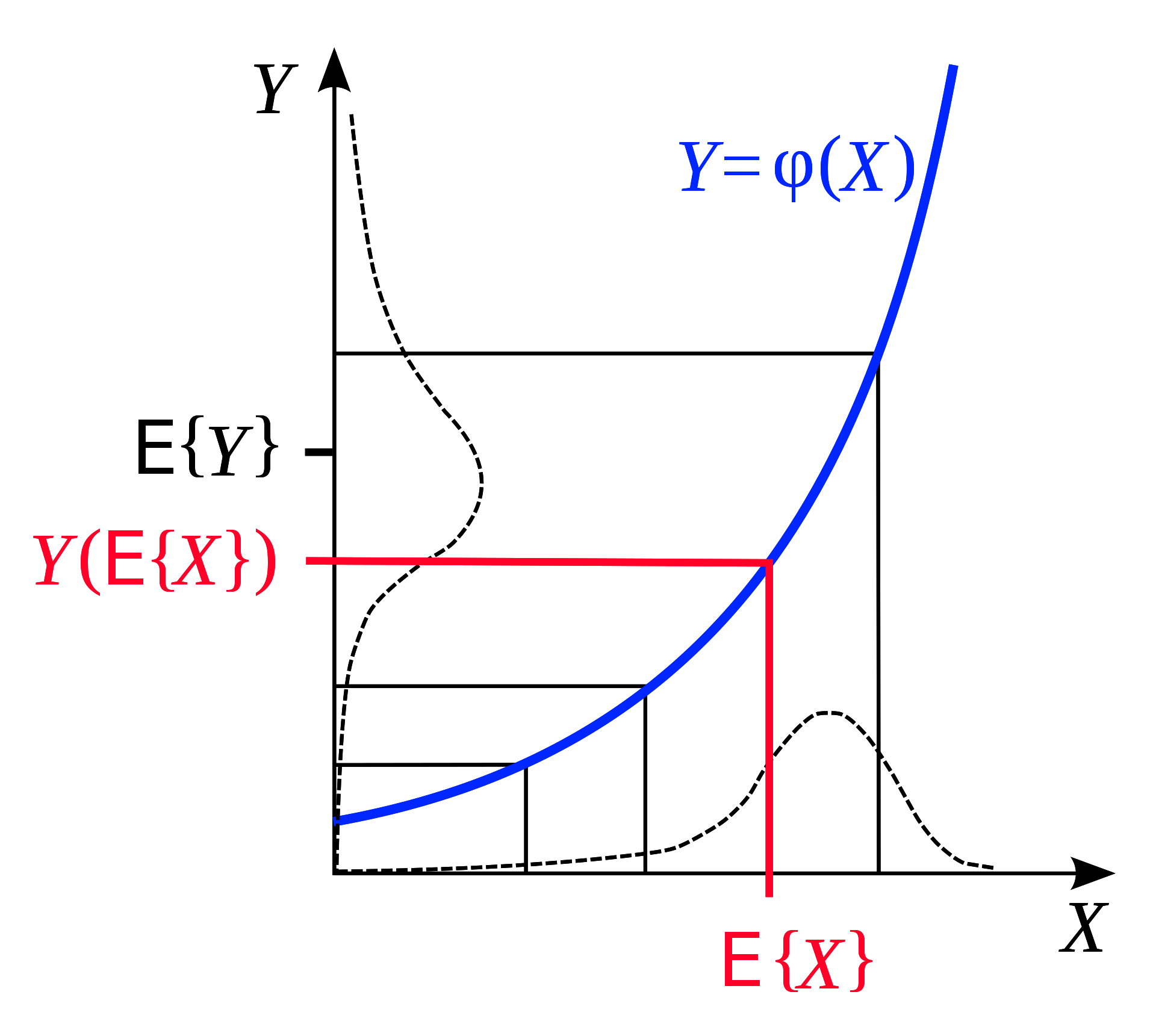
Figure 6: Jensen's Inequality (taken from [Wikipedia](https://en.wikipedia.org/wiki/Jensen%27s_inequality))
Asimismo, si $F$ es convexo, para una distribución de probabilidad fija $q$, podemos inferir de la Desigualdad de Jensen que en el rango $z$,
$$F\Bigg(\int_z q(z)h(z)\Bigg) \leq \int_z q(z)F(h(z)) \tag{1}$$
Ahora, recuerde que nuestro $L (x, y)$ marginado después de la multiplicación con $\frac {q (z)} {q (z)}$ es,
$$L(x,y) = -\frac{1}{\beta}\int_z q(z) \frac{\exp({-\beta E(x,y,z)})}{q(z)}$$
Si hacemos $h(z) = -\frac{1}{\beta} \frac{\exp({-\beta E(x,y,z)})}{q(z)}$, sabemos de la desigualdad de Jensen $(1)$ que
$$F\Bigg(\int_z q(z)\frac{\exp({-\beta E(x,y,z)})}{q(z)}\Bigg) \leq \int_z q(z)F\Bigg(\frac{\exp({-\beta E(x,y,z)})}{q(z)}\Bigg)$$
Continuemos trabajando esto, con una función de pérdida convexa concreta, $F(x) = - \log(x)$
$$-\log\Bigg(-\frac{1}{\beta}\int_z q(z)\frac{\exp({-\beta E(x,y,z)})}{q(z)}\Bigg) \leq \int_z q(z) * \frac{-1}{\beta}\log\Bigg(\frac{\exp({-\beta E(x,y,z)})}{q(z)}\Bigg)$$
$$\leq \int_z q(z)[E(x,y,z) + \frac{1}{\beta}\log(q(z))]$$
$$\leq \int_z q(z)E(x,y,z) + \frac{1}{\beta}\int_z q(z)\log(q(z))$$
¡Excelente! Ahora tenemos un límite superior para nuestra función de pérdida $L (x, y)$, compuesto por dos términos que entendemos. El primer término $\int_z q (z) E (x, y, z)$ es la energía *promedio*. Y el segundo término $\frac{1} {\beta} \int_z \log (q (z))$ es solo un factor ($ - \frac {1} {\ beta}$) multiplicado por la *entropía* del distribución $q$.
## ¿Cuál es el punto?
Ahora hemos formulado un límite superior de tal manera que podemos evitar integraciones complicadas y, en cambio, simplemente aproximar estos valores tomando muestras de una distribución sustituta ($q(z)$) ¡de nuestra elección!
Para obtener el valor del primer término de nuestra función de límite superior, simplemente tomamos una muestra de esa distribución y calculamos el valor promedio de $L$ que obtenemos aplicando nuestros $z$ de muestra.
El segundo término (un factor de entropía) es solo una propiedad de la familia de distribución, y también puede aproximarse con un muestreo aleatorio de $ q $.
Finalmente, podemos minimizar $L$ con respecto a sus parámetros (digamos, pesos de una red $W$), minimizando esta función que limita $L$ arriba. Llevamos a cabo esta minimización actualizando nuestras dos variables: (1) la entropía de $ q $ y (2) los parámetros de nuestro modelo $ W $.
## Resumen
Ésta es la "visión energética" de la inferencia variacional. Si necesita calcular el logaritmo de una suma de exponenciales, reemplácelo con el promedio de su función más un término de entropía. Esto nos da un límite superior. Luego minimizamos este límite superior y, al hacerlo, minimizamos la función que realmente nos importa.
📝
Yada Pruksachatkun, Ananya Harsh Jha, Joseph Morag, Dan Jefferys-White, and Brian Kelly
lcipolina (Lucia Cipolina-Kun)
15 Sep 2020





