Aprendizaje profundo para prediccion estructurada

Predicción estructurada

Es el problema de predecir la variable ‘y’ para una entrada ‘x’ dada que es mutuamente dependiente y restringida, en lugar de valores escalares discretos o reales. La variable de salida no pertenece a una sola categoría, sino que puede tener un numero de valores posibles exponenciales o infinitos. Por ejemplo: en el caso de reconocimiento de voz, escritura a mano o traducción de lenguaje natural, la salida debe ser gramaticalmente correcta y no es posible limitar el número de posibilidades de salida. La tarea del modelo es capturar la estructura secuencial, espacial o combinatorial en el dominio del problema.

Primeros trabajos sobre predicción estructurada

Este vector se alimenta a un TDNN que proporciona un vector de características que, en el caso de los sistemas modelo, se puede comparar con softmax, el cual representa una categoría. Un problema que surge en el caso de reconocer la palabra que se pronunció, es que diferentes personas pueden pronunciar la misma palabra de diferentes formas y velocidades. Para resolver esto se utiliza “Deformación en Tiempo Dinámico”.

La idea es proporcionar al sistema un conjunto de plantillas (templates) pregrabadas que correspondan a vectores de secuencia o características que alguien haya registrado. La red neuronal se entrena al mismo tiempo que la plantilla para que el sistema aprenda a reconocer la palabra en diferentes pronunciaciones. La variable latente nos permite deformar en el tiempo el vector de características para que coincida con la longitud de las plantillas.

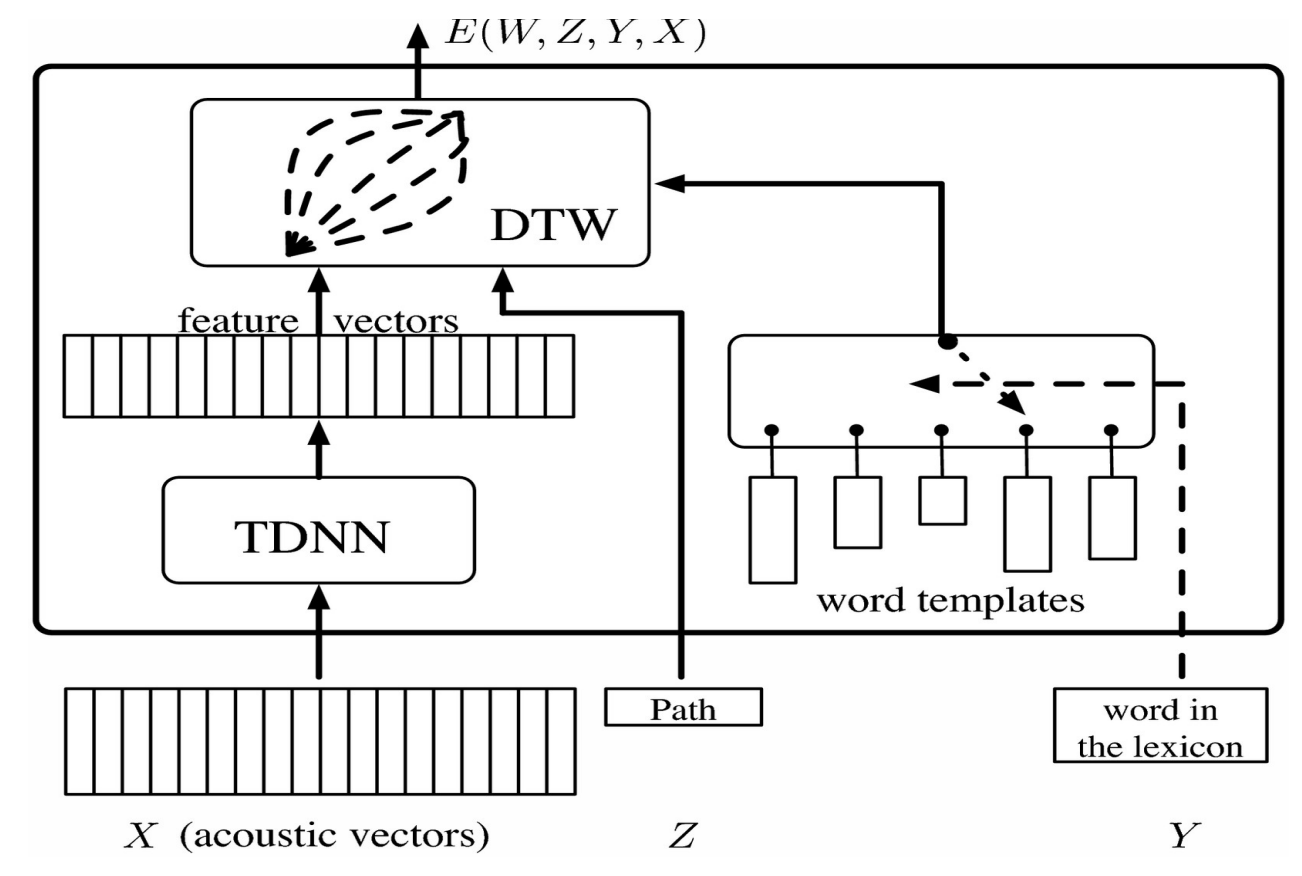
Figura 1.

Esto se puede visualizar como una matriz ordenando los vectores de características de TDNN horizontalmente y las plantillas de palabras verticalmente. Cada entrada en la matriz corresponde a la distancia entre el vector de características. Esto se puede visualizar como un problema de grafos en el que el objetivo es comenzar desde la esquina inferior izquierda y llegar a la esquina superior derecha atravesando el camino que minimiza la distancia.

Para entrenar este modelo de variable latente, necesitamos hacer que la energía para las respuestas correctas sea lo más pequeña posible y más grande para cada respuesta incorrecta. Para hacer esto, usamos una función objetivo que toma plantillas para palabras incorrectas y las aleja de la secuencia actual de características y propaga hacia atrás los gradientes.

Grafos de factores basados en energía

La idea detrás de los grafos de factores basados en energía es construir un modelo basado en “energía” en el que la energía es la suma de términos parciales de energía cuando la probabilidad es un producto de factores. El beneficio de estos modelos es que se pueden emplear algoritmos de inferencia eficientes.

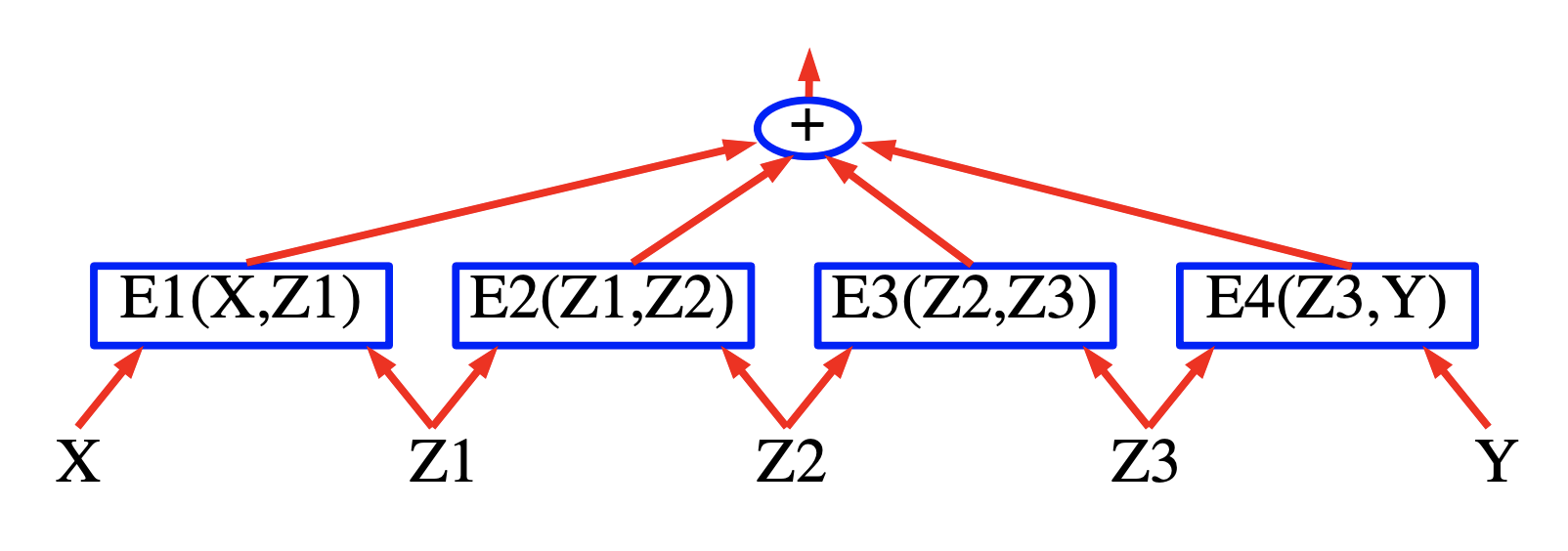
Figura 2.

Etiquetado de secuencia

El modelo toma una señal de entrada de voz ‘X’ y devuelve las etiquetas ‘Y’ de manera que las etiquetas de salida minimizan el término de energía total.

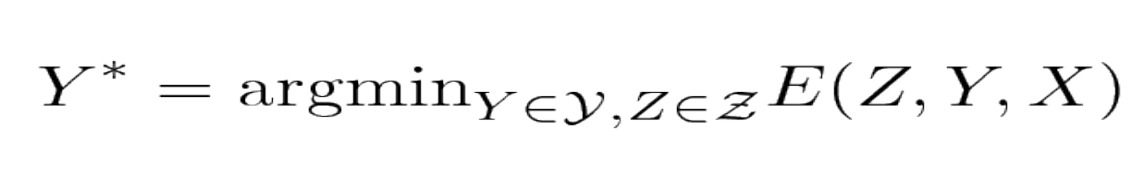
Figura 3.

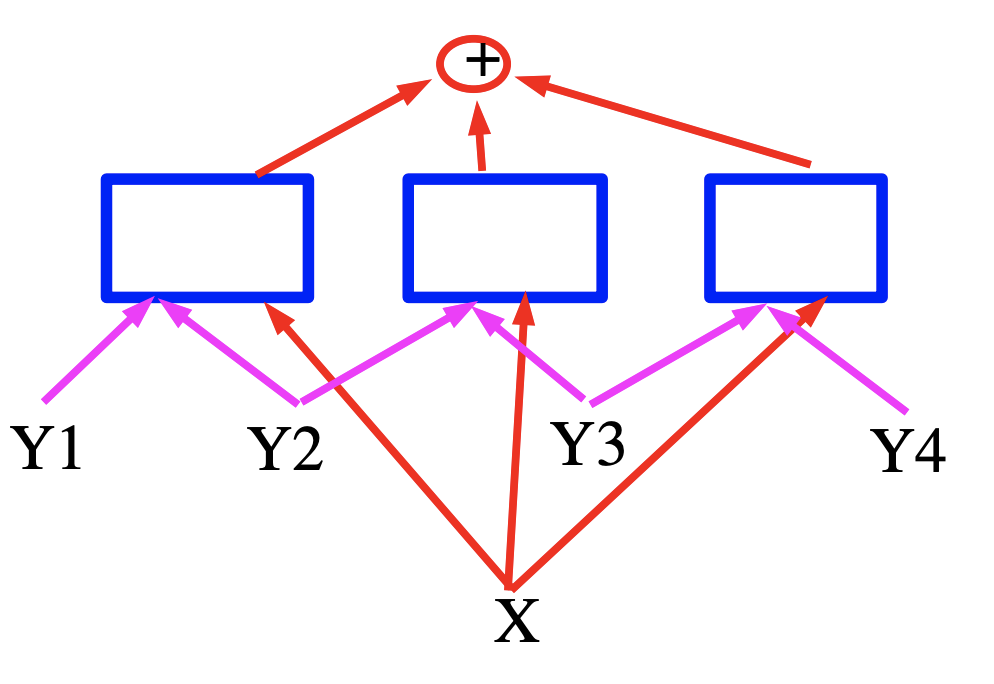
Figura 4.

En este caso, la energía es una suma de tres términos representados por los cuadrados azules que son redes neuronales que producen vectores de características para las variables de entrada. En el caso del reconocimiento de voz, la ‘X’ se puede considerar como una señal de voz y los cuadrados implementan las restricciones gramaticales, las ‘Y’ representan las etiquetas de salida generadas.

Inferencia eficiente para gráficos de factores basados en energía

Un tutorial sobre el aprendizaje basado en la energía (Yann LeCun, Sumit Chopra, Raia Hadsell, Marc’Aurelio Ranzato y Fu Jie Huang 2006):

El aprendizaje y la inferencia con modelos basados en energía implican una minimización de la energía sobre el conjunto de respuestas $\mathcal {Y}$ y variables latentes $\ mathcal {Z}$. Cuando la cardinalidad de $\ mathcal {Y} \ times \ mathcal {Z}$ es grande, esta minimización puede volverse intratable. Una forma de abordar el problema es aprovechar la estructura de la función energética para realizar la minimización de manera eficiente. Un caso en el que se puede explotar la estructura ocurre cuando la energía se puede expresar como una suma de funciones individuales (llamadas factores) que dependen de diferentes subconjuntos de las variables en Y y Z. Estas dependencias se expresan mejor en la forma de un factor grafico. Los grafos de factores son una forma general de modelos de grafos o de “redes de creencias”.

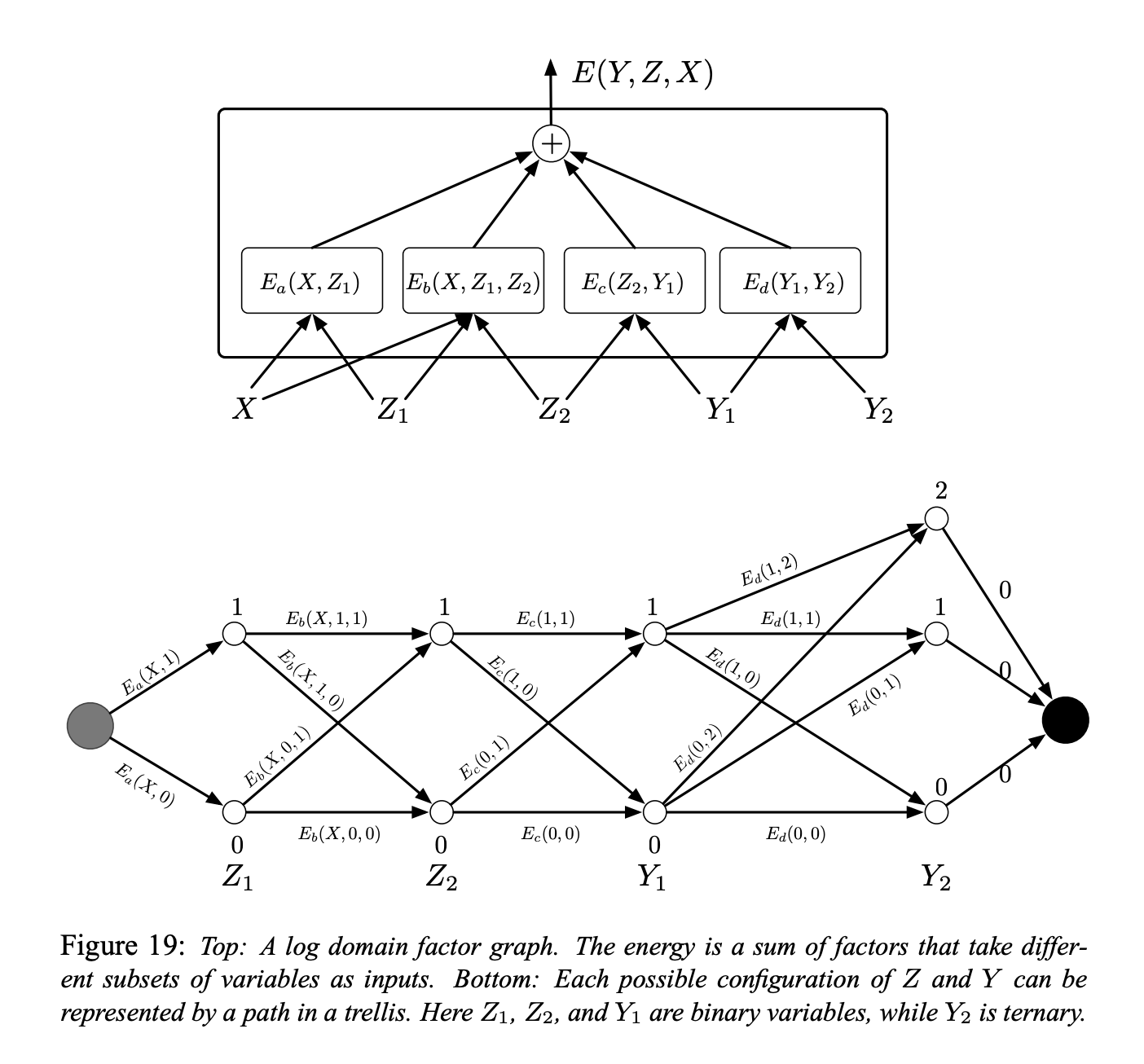
Figura 5.

En la Figura (arriba) se muestra un ejemplo simple de un gráfico de factores. La función de energía es la suma de cuatro factores:

donde $Y = [Y_1, Y_2]$ son las variables de salida y $Z = [Z_1, Z_2]$ son las variables latentes. Cada factor puede verse como una representación de restricciones suaves entre los valores de sus variables de entrada. El problema de la inferencia consiste en encontrar:

Supongamos que $Z_1$, $ Z_2$ y $ Y_1$ son variables binarias discretas y que $ Y_2$ es una variable ternaria. La cardinalidad del dominio de $ X$ es inmaterial ya que X siempre es observable. El número de configuraciones posibles de $ Z$ y $ Y$ dado X es $2 \times 2 \times 2 \times 3 = 24$. Un algoritmo de minimización ingenuo a través de una búsqueda exhaustiva evaluaría la función de energía completa 24 veces (96 evaluaciones de un solo factor).

Sin embargo, notamos que para un $X$ dado, $E_a$ solo tiene dos configuraciones de entrada posibles: $Z_1 = 0$ y $Z_1 = 1$. De manera similar, $E_b$ y $E_c$ solo tienen 4 configuraciones de entrada posibles, y $E_d$ tiene 6. Por lo tanto, no hay necesidad de más de $2 + 4 + 4 + 6 = 16$ evaluaciones de un solo factor.

Por lo tanto, podemos calcular previamente los 16 valores de los factores y colocarlos en los arcos en una grilla como se muestra en la Figura de arriba (parte inferior).

Los nodos de cada columna representan los posibles valores de una sola variable. Cada flanco está ponderado por la energía de salida del factor para los valores correspondientes de sus variables de entrada. Con esta representación, una única ruta desde el nodo inicial al nodo final representa una posible configuración de todas las variables. La suma de los pesos a lo largo de un camino es igual a la energía total para la configuración correspondiente. Por lo tanto, un problema de inferencia se puede reducir a buscar la ** ruta más corta ** en este gráfico. Esto se puede realizar utilizando un método de programación dinámica como el algoritmo de Viterbi o el algoritmo A *. El costo es proporcional al número de aristas (16), que es exponencialmente menor que el número de caminos en general.

Para calcular $E (Y, X) = \ min_ {z \ in Z} E (Y, z, X)$, seguimos el mismo procedimiento, pero restringimos el grafo al subconjunto de arcos que son compatibles con el valor de $Y$.

El procedimiento anterior a veces se denomina algoritmo de suma mínima y es la versión de dominio de registro del producto máximo tradicional para modelos gráficos. El procedimiento se puede generalizar fácilmente a grafos de factores donde los factores toman más de dos variables como entradas, y a grafos de factores que tienen una estructura de árbol en lugar de una estructura de cadena.

Sin embargo, solo se aplica a los grafos de factores que son árboles bipartitos (sin bucles). Cuando hay bucles en el gráfico, el algoritmo de suma mínima puede dar una solución aproximada cuando se repite, o puede que no converja en absoluto. En este caso, se podría utilizar un algoritmo de descenso como el annealing.

Grafos simples de factores basados ​​en energía con factores “superficiales”

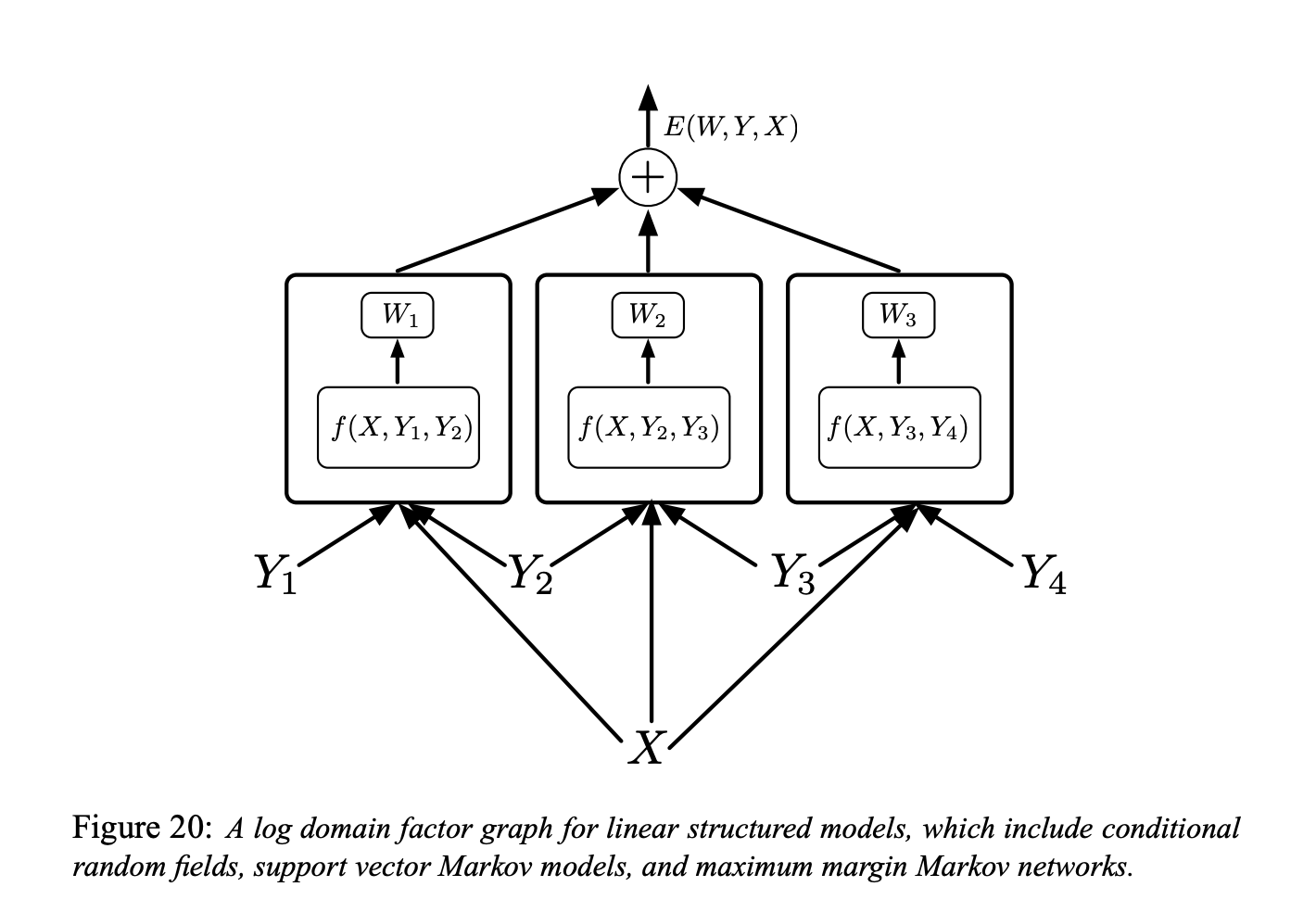
Figura 6.

El grafo de factores que se muestra en la Figura anterior es un grafo de factores de dominio logarítmico para modelos estructurados lineales (estamos hablando de “grafos de factores simples basados ​​en energía”)

Cada factor es una función lineal de los parámetros entrenables. Depende de la entrada y de un par de etiquetas individuales $(Y_m, Y_n)$. En general, cada factor podría depender de más de dos etiquetas individuales, pero limitaremos la discusión a factores por pares para simplificar la notación:

Aquí $\ mathcal {F}$ denota el conjunto de factores (el conjunto de pares de etiquetas individuales que tienen una interdependencia directa), $W_ {mn}$ es el vector de parámetro para el factor $(m, n),$ y $f_ {mn} \ left (X, Y_ {m}, Y_ {n} \ right)$ es un vector de características (fijo). El vector de parámetro global $W$ es la concatenación de todos los $W_ {m n}.$

Y luego podemos pensar en qué tipo de función de pérdida utilizar. Aquí vienen varios modelos diferentes.

Campo aleatorio condicional

Podemos usar la función de pérdida de probabilidad logarítmica negativa para entrenar un modelo estructurado lineal.

Este es el campo aleatorio condicional

La intuición es que queremos la energía de la respuesta correcta a la ecuacion debajo y ademas queremos que el logaritmo de exponencial para todas las respuestas, incluida la buena, sea grande.

A continuación se muestra la definición formal de la función de pérdida de probabilidad logarítmica negativa:

Redes de márgenes de margen máximo y SVM latente

También podemos utilizar la función de pérdida “de bisagra” para la optimización.

La intuición detrás es que queremos que la energía de la respuesta correcta sea baja, y luego entre todas las configuraciones posibles de respuestas incorrectas, vamos a buscar la que tenga la energía más baja entre todas las equivocadas o malas. Luego vamos a impulsar la energía de este. No necesitamos aumentar la energía para las otras respuestas malas porque de todos modos son más grandes.

Modelo de perceptrón estructurado

Podemos entrenar el modelo estructurado lineal usando la pérdida de perceptrón.

Collins [Collins, 2000, Collins, 2002] ha abogado por su uso para modelos estructurados lineales en el contexto de la PNL:

donde $Y ^ {* i} = \operatorname {argmin} _ {y \ in \mathcal {Y}} E \left (W, y, X ^ {i} \right)$ es la respuesta producida por el sistema.

Primeras pistas sobre entrenamiento discriminativo para reconocimiento de voz y escritura a mano.

Pérdida mínima por error empírico (Ljolje y Rabiner 1990):

Al entrenar a nivel de secuencia, no le especifican dicen al sistema el sonido o la ubicación. Sino que le dan al sistema una oración de entrada y la transcripción en términos de palabras, y le piden al sistema que la resuelva haciendo deformaciones de tiempo. No usaban redes neuronales ya que tenían otras formas de convertir las señales del habla en categorías de sonido.

Red del transformador gráfico

Aquí el problema es que tenemos una secuencia de dígitos en la entrada y no sabemos cómo hacer la segmentación. Lo que podemos hacer es construir un grafo en el que cada camino es una forma de romper la secuencia de caracteres, y vamos a encontrar el camino con menor energía, que básicamente es encontrar el camino más corto. Aquí hay un ejemplo concreto de cómo funciona.

Tenemos la imagen de entrada 34. Ejecute esto a través del segmentador y obtenga múltiples segmentaciones alternativas. Estas segmentaciones son formas de agrupar estas manchas de cosas. Cada ruta en el grafo de segmentación corresponde a una forma particular de agrupar las manchas de tinta.

Figura 7.

Pasamos cada uno por el mismo ConvNet de reconocimiento de caracteres y obtenemos una lista de 10 puntuaciones (aqui hay dos, pero esencialmente deberían ser 10, que representan 10 categorías). Por ejemplo, 1 [0.1] significa que la energía es 0.1 para la categoría 1. Así que obtengo una gráfica aquí, y puedes pensar en ella como una forma extraña de tensor. Realmente es un tensor escaso. Es un tensor que dice que “para cada posible configuración de esta variable, dime el costo de la variable”. Es más como una distribución sobre tensores o distribución logarítmica porque estamos hablando de energías.

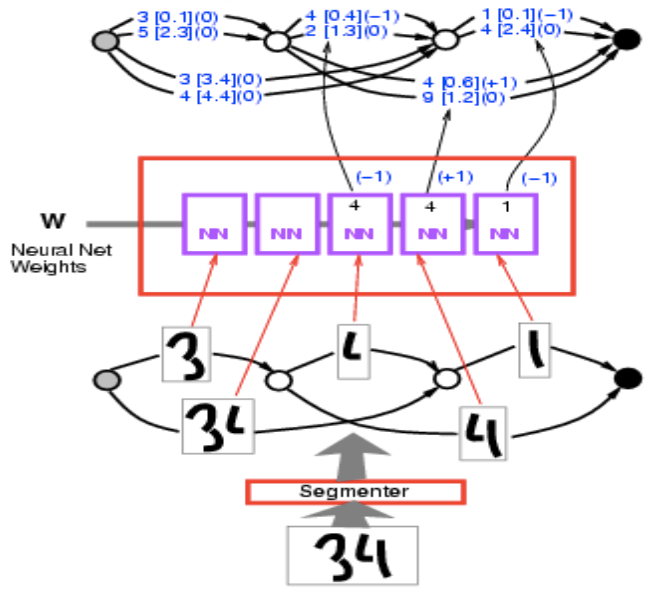
Figura 8.

Toma esta gráfica y calcula la energía de la respuesta correcta. Le estoy diciendo que la respuesta correcta es 34. Selecciona dentro de esos caminos y encuentra los que dicen 34. Hay dos de ellos, uno de energía 3.4 + 2.4 = 5.8, y el otro 0.1 + 0.6 = 0.7. Elije el camino con la energía más baja. Aquí obtenemos el camino con energía 0.7.

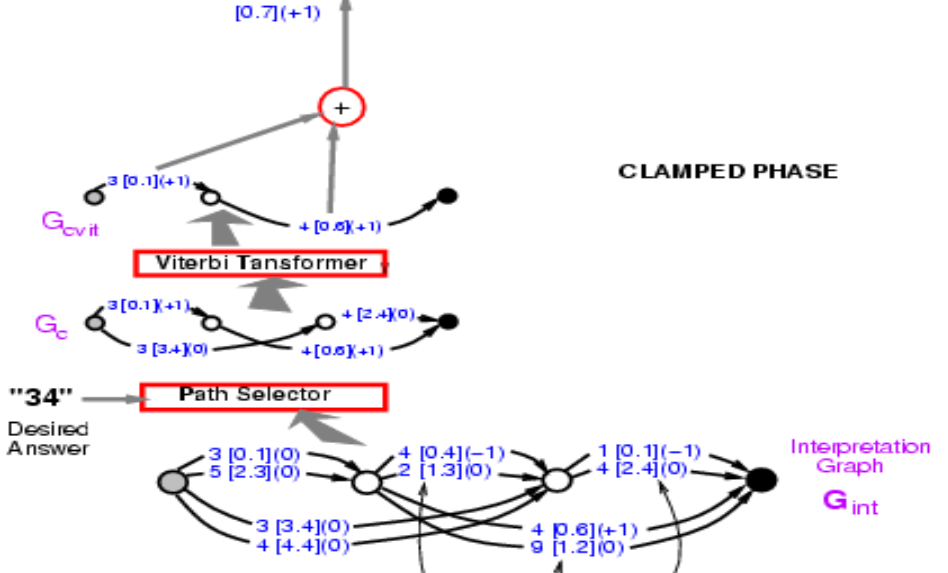
Figura 9.

Entonces, encontrar la ruta es como minimizar la variable latente donde la variable latente es la ruta que elijas. Conceptualmente, es un modelo energético con una variable latente como camino.

Ahora tenemos la energía del camino correcto, 0,7. Lo que tenemos que hacer ahora es propagar el gradiente a través de toda esta estructura, de modo que podamos cambiar el peso en la ConvNet de tal manera que la energía final disminuya. Parece abrumador, pero es completamente posible. Debido a que todo este sistema está construido con elementos que ya conocemos, la red neuronal es regular y el selector de ruta y el transformador de Viterbi son básicamente “switches” o “alternadores” que eligen un borde en particular o no.

Entonces, ¿cómo propagamos hacia atrás? Bueno, el punto 0.7 es la suma de 0.1 y 0.6. Entonces, tanto el punto 0.1 como el 0.6 tendrán gradiente +1, que se indican entre paréntesis. Luego, el transformador de Viterbi simplemente selecciona una ruta entre dos. Así que simplemente copia el gradiente para el borde correspondiente en el gráfico de entrada y establezca el grado para otras rutas que no estén seleccionadas como cero. Es exactamente lo que está sucediendo en Max-Pooling o Mean-Pooling. El selector de ruta es el mismo, es solo un sistema que selecciona la respuesta correcta. Tenga en cuenta que 3 [0.1] (0) en el gráfico debe ser 3 [0.1] (1) en esta etapa, y volveremos a esto más adelante. Luego, puede propagar el gradiente hacia atrás a través de la red neuronal. Eso hará que la energía de la respuesta correcta sea pequeña.

Lo importante aquí es que esta estructura es dinámica en la esencia de que si le doy una nueva entrada, el número de instancias de red neuronal cambiará con el número de segmentaciones, y los gráficos derivados también cambiarán. Necesitamos retropropagar a través de esta estructura dinámica. Esta es la situación donde cosas como PyTorch son realmente importantes.

Esta fase de retropropagación reduce la energía de la respuesta correcta. Y habrá una segunda fase en la que aumentaremos la energía de la respuesta incorrecta. En este caso, simplemente dejamos que el sistema elija la respuesta que desee. Esta será una forma simplificada de entrenamiento discriminativo para la predicción de estructuras que utiliza la pérdida de percepción.

Las primeras etapas de la fase dos son exactamente las mismas que las de la primera. El Transformador de Viterbi solo elige el mejor camino con la energía más baja, no nos importa si este camino es correcto o no aquí. La energía que obtienes aquí será menor o igual a la que obtienes de la fase uno, ya que la energía que obtienes aquí es la más pequeña entre todos los caminos posibles.

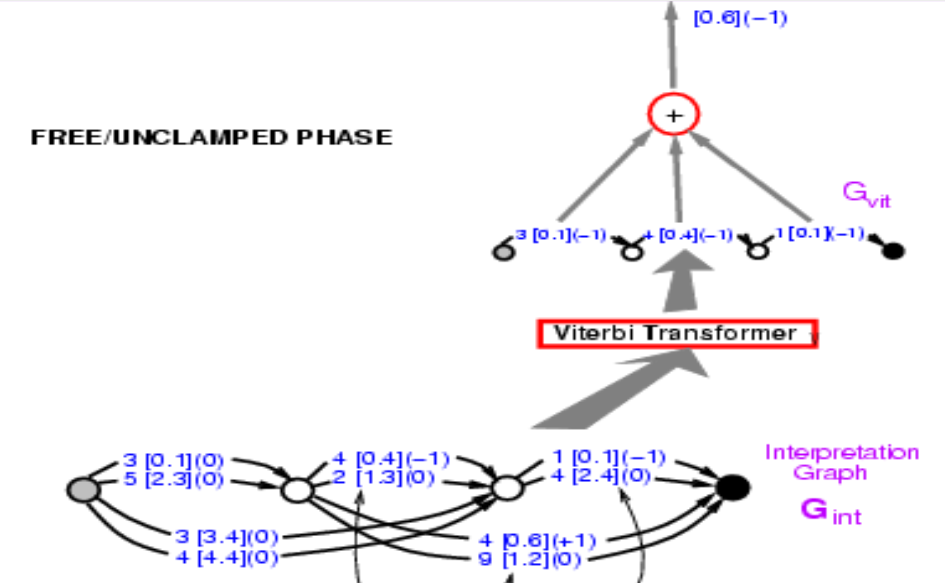
Figura 10.

Juntando las fases uno y dos. La función de pérdida debe ser energía1 - energía2. Antes, presentamos como propagar hacia atrás a través de la parte izquierda, y ahora realmente necesitamos propagar hacia atrás a través de toda la estructura. Cualquier camino en el lado izquierdo obtendrá +1, y cualquier camino en el lado derecho obtendrá -1. Entonces apareció 3 [0.1] en ambos caminos, por lo que debería obtener un gradiente 0. Si hacemos esto, el sistema eventualmente minimizará la diferencia entre la energía de la respuesta correcta y la energía de la mejor respuesta cualquiera que sea. La función de pérdida aquí es la pérdida de perceptrón.

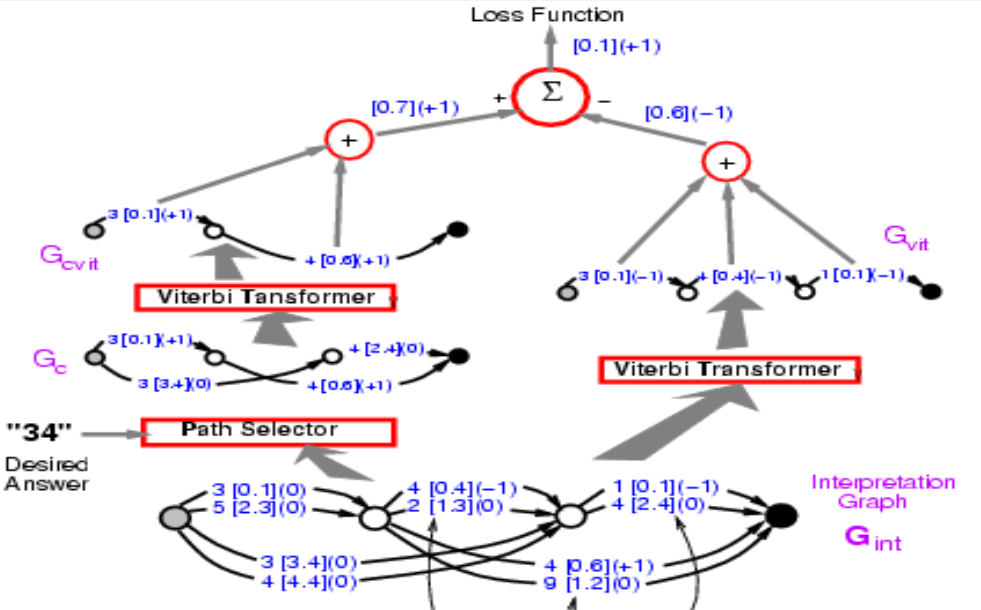
Figura 11.

Preguntas y respuestas de comprensión

Pregunta 1: ¿Por qué es fácil la inferencia en el caso de grafos de factores basados en energía?

La inferencia en el caso del modelo basado en energía con variable latente implica el uso de técnicas exhaustivas como el descenso de gradiente para minimizar la energía, sin embargo, ya que la energía, en este caso, es la suma de factores y se pueden utilizar técnicas como la programación dinámica.

Pregunta 2: ¿Qué pasa si las variables latentes en los gráficos de factores son variables continuas? ¿Podemos seguir usando el algoritmo de suma mínima?

No podemos porque ahora no podemos buscar todas las combinaciones posibles para todos los valores de los factores. Sin embargo, en este caso, las energías también nos dan una ventaja, porque podemos hacer optimizaciones independientes. Como la combinación de $Z_1$ y $Z_2$ solo afecta a $E_b$. Podemos hacer una optimización independiente y programación dinámica para hacer la inferencia.

Pregunta 3: ¿Los cuadros NN se refieren a ConvNets separados?

Son compartidos. Son varias copias de la misma ConvNet. Es solo una red de reconocimiento de personajes.