Redes Convolucionales en Grafos III

Introducción a las Redes Convolucionales de Grafos(GCN)

Las Redes Convolucionales de Grafos (GCN) son un tipo de arquitectura que utilizan la estructura de los datos. Antes de entrar en detalles, hagamos una revisión rápida sobre la auto-atención, dado que las GCN y la auto-atención son conceptualmente relevantes.

Revisión: Auto-atención

• En auto-atención, tenemos un conjunto de entradas $\lbrace\boldsymbol{x}_{i}\rbrace^{t}_{i=1}$. A diferencia de una secuencia, este conjunto no tiene un orden.
• El vector oculto $\boldsymbol{h}$ viene dado por una combinación linear de los vectores en el conjunto.
• Esto lo podemos expresar como $\boldsymbol{X}\boldsymbol{a}$ utilizando una multiplicación matriz vector, donde $\boldsymbol{a}$ contiene los coeficientes que escalan al vector de entrada $\boldsymbol{x}_{i}$.

Para una explicación detallada, consulta las notas de la Semana 12.

Notación

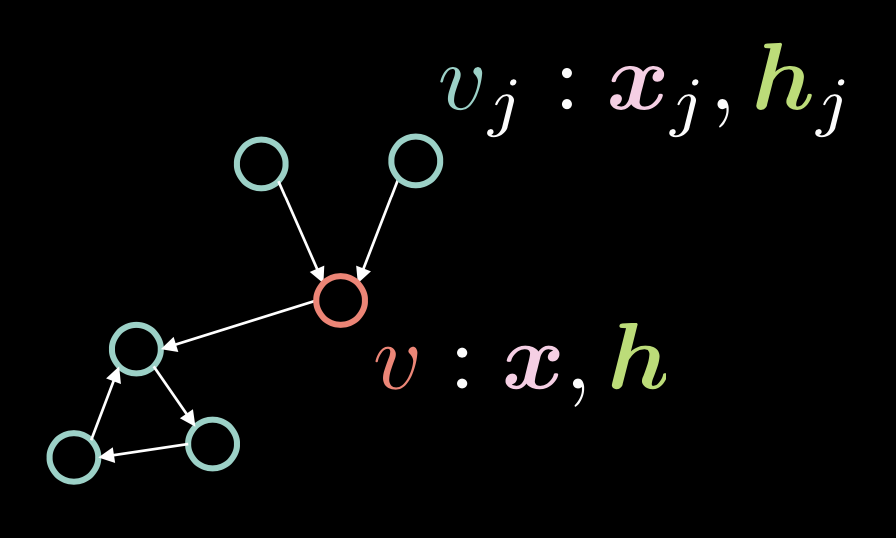
Fig. 1: Red Convolucional de Grafos

En la Figura 1, el vértice $v$ está formado por dos vectores: el vector de entrada $\boldsymbol{x}$ y su representación oculta $\boldsymbol{h}$. Tenemos también múltiples vértices $v_{j}$, que están formados por $\boldsymbol{x}_j$ y $\boldsymbol{h}_j$. En este grafo, los vértices están conectados por ejes dirigidos.

Representamos estos ejes dirigidos con un vector de adyacencia $\boldsymbol{a}$, donde cada elemento $\alpha_{j}$ tiene asignado un $1$ si hay eje de $v_{j}$ a $v$.

El grado (número de ejes entrantes) $d$ se define como la norma de este vector de adyacencia, es decir $\Vert\boldsymbol{a}\Vert_{1} $, que es el número de unos en el vector $\boldsymbol{a}$.

El vector oculto $\boldsymbol{h}$ se determina mediante la siguiente expresión:

donde $f(\cdot)$ es una función no lineal como ReLU $(\cdot)^{+}$, Sigmoidal $\sigma(\cdot)$ y la tangente hiperbólica $\tanh(\cdot)$.

El término $\boldsymbol{U}\boldsymbol{x}$ tiene en cuenta al vértice $v$ en sí mismo, aplicando la rotación $\boldsymbol{U}$ a la entrada $v$.

Recuerda que en auto-atención, el vector oculto $\boldsymbol{h}$ se calcula como $\boldsymbol{X}\boldsymbol{a}$, lo que significa que se hace un escalado de las columnas de $\boldsymbol{X}$ con los factores en $\boldsymbol{a}$. En el contexto de las GCN, esto significa que si tenemos múltiples ejes entrantes, es decir, múltiples unos en el vector de adyacencia $\boldsymbol{a}$, $\boldsymbol{X}\boldsymbol{a}$ aumentará. Por otra parte, si solo tenemos un eje entrante, este valor disminuye. Para solucionar el problema de que el valor sea proporcional al número de ejes entrantes, lo dividimos por el número total de ejes entrantes $d$. Después aplicamos la rotación $\boldsymbol{V}$ a $\boldsymbol{X}\boldsymbol{a}d^{-1}$.

Podemos representar está representación oculta $\boldsymbol{h}$ para el conjunto entero de entradas $\boldsymbol{x}$ utilizando la siguiente notación matricial:

donde $\vect{D} = \text{diag}(d_{i})$.

Teoría de Residual Gated GCN con código

Las Redes convolucionales de Grafos “Residual Gated” son un tipo de GCN que se pueden representar como se muestra en la Figura 2:

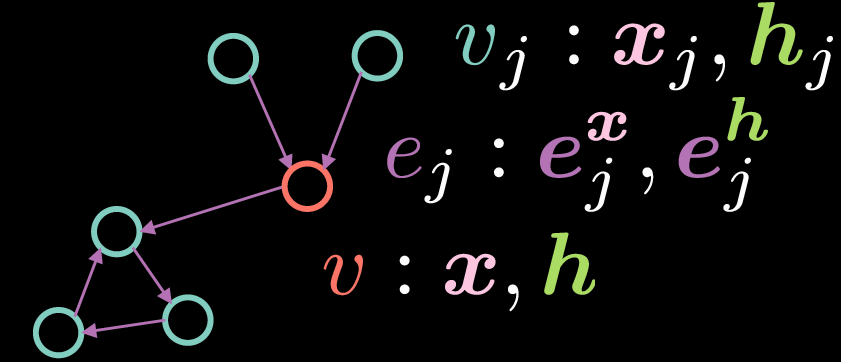
Fig. 2: Red Convolucional de Grafos Residual Gated

Al igual que con las GCN estándar, el vértice $v$ consiste en dos vectores: la entrada $\boldsymbol{x}$ y su representación oculta $\boldsymbol{h}$. Sin embargo, en este caso, los ejes también tienen una representación de características, donde $\boldsymbol{e_{j}^{x}}$ representa la representación del eje de entrada y $\boldsymbol{e_{j}^{h}}$ representa la representación del eje oculto.

La representación $\boldsymbol{h}$ del vértice $v$ se calcula mediante la siguiente ecuación:

donde $\boldsymbol{x}$ es la representación de la entrada, $\boldsymbol{Ax}$ representa una rotación aplicada a la entrada $\boldsymbol{x}$ y $\sum_{v_j→v}{\eta(\boldsymbol{e_{j}})\odot \boldsymbol{Bx_{j}}}$ denota el sumatorio de la multiplicación elemento a elemento de las características de entrada rotadas y una compuerta (gate) $\eta(\boldsymbol{e_{j}})$. A diferencia de la antedicha GCN, donde promediamos las representaciones entrantes, el término compuerta es crítico para la implementación de las Residual Gated GCN, ya que nos permite modular las representaciones de entrada en base a las representaciones de los ejes.

Nótese que la suma es solo sobre los vértices ${v_j}$ que tienen ejes entrantes en el vértice ${v}$. El término residual (en las Residual Gated GCN) viene del hecho de que para calcular la representación oculta $\boldsymbol{h}$, sumamos la representación de entrada $\boldsymbol{x}$. El término compuerta $\eta(\boldsymbol{e_{j}})$ se calcula como se muestra a continuación:

El valor de la compuerta $\eta(\boldsymbol{e_{j}})$ es una sigmoidal normalizada que se obtiene dividiendo la sigmoidal de la representación del eje entrante por la suma de las sigmoidales de las representaciones de todos los ejes entrantes. Nótese que para calcular el término compuerta, necesitamos la representación del eje $\boldsymbol{e_{j}}$, que podemos calcular utilizando las siguientes ecuaciones:

La representación del eje oculto $\boldsymbol{e_{j}^{h}}$ se obtiene mediante el sumatorio de la representación del eje inicial $\boldsymbol{e_{j}^{x}}$ y $\texttt{ReLU}(\cdot)$ aplicada a $\boldsymbol{e_{j}}$, donde $\boldsymbol{e_{j}}$ por su parte viene dada por por la suma de una rotación aplicada a $\boldsymbol{e_{j}^{x}}$, una rotación aplicada a la representación de entrada $\boldsymbol{x_{j}}$ del vértice $v_{j}$ y una rotación aplicada a la representación de entrada $\boldsymbol{x}$ del vértice $v$.

Nota: Para calcular las representaciones ocultas descendientes (por ejemplo* la representación oculta de la $2^\text{ª}$ capa), podemos reemplazar las representaciones de entrada por la representación de características de la $1^\text{ª}$ capa en las ecuaciones arriba mencionadas.*

Clasificación de grafos y Capa Residual Gated GCN

En esta sección, introducimos el problema de clasificación de grafos y escribiremos código para una capa Residual Gated GCN. Además de utilizar las instrucciones de import habituales, añadiremos las siguientes:

os.environ['DGLBACKEND'] = 'pytorch'
import dgl
from dgl import DGLGraph
from dgl.data import MiniGCDataset
import networkx as nx

La primera linea instruye a DGL para que utilice PyTorch como backend. Deep Graph Library (DGL) proporciona diversas funcionalidades sobre grafos, mientras que networkx nos permite visualizar estos grafos.

En este notebook, la tarea es clasificar una estructura de grafo dada en uno de 8 tipos de grafos. La base de datos obtenida de dgl.data.MiniGCDataset nos proporciona un número de grafos (num_graphs) con un número de nodos entre min_num_v y max_num_v. Por ello, no todos los grafos obtenidos tendrán el mismo número de nodos/verices.

Nota: Para familiarizarte de forma básica con DGLGraphs, se recomienda leer este tutorial corto.

Habiendo creado los grafos, la siguiente tarea es añadir alguna señal al dominio. Se pueden aplicar características a nodos y ejes de un DGLGraph. Las características vienen representadas por un diccionario de nombres (strings) y tensores (fields). ndata y edata son azúcar sintáctico para acceder a las características de todos los nodos y ejes.

El siguiente fragmento de código muestra como se generan las características. A cada nodo se le asigna un valor igual al número de ejes entrantes, mientras que a cada eje se le asigna el valor 1.

def create_artificial_features(dataset):
    for (graph, _) in dataset:
        graph.ndata['feat'] = graph.in_degrees().view(-1, 1).float()
        graph.edata['feat'] = torch.ones(graph.number_of_edges(), 1)
    return dataset

A continuación se muestra como se crean los conjuntos de entrenamiento y test y se asignan las características:

trainset = MiniGCDataset(350, 10, 20)
testset = MiniGCDataset(100, 10, 20)

trainset = create_artificial_features(trainset)
testset = create_artificial_features(testset)

Una muestra de un grafo del set de entrenamiento tiene la siguiente representación. Aquí, observamos que el grafo tiene 15 nodos y 45 ejes; y que tanto los nodos como los ejes tienen una representación de características de forma (1,), como es de esperar. Además, el 0 significa que éste grafo pertenece a la case 0.

(DGLGraph(num_nodes=15, num_edges=45,
         ndata_schemes={'feat': Scheme(shape=(1,), dtype=torch.float32)}
         edata_schemes={'feat': Scheme(shape=(1,), dtype=torch.float32)}), 0)

Nota sobre las funciones Message y Reduce de DGL

En DGL, las funciones mensaje son expresadas como Edge UDF (User Defined Funcions, funciones definidas por el usuario). Las funciones Edge UDF toman un solo argumento edges. Tiene tres miembros src, dst, y data para acceder a las características de los nodos fuente, las características de los nodos destino y las características de los ejes, respectivamente. Las funciones reduce son Node UDF. Los Node UDF tienen un solo argumento nodes, que tiene dos miembros data y mailbox. data contiene las características del nodo y mailbox contiene todas las características de mensajes entrantes, apiladas en la segunda dimensión (por eso el argumento dim=1). update_all(message_func, reduce_func) envía mensajes a través de todos los ejes y actualiza todos los nodos.

Implementación de la capa Gated Residual GCN

Una capa Gated Residual GCN se implementa como se muestra en el fragmento de código que sigue.

Primero, todas las rotaciones de características entrantes $\boldsymbol{Ax}$, $\boldsymbol{Bx_{j}}$, $\boldsymbol{Ce_{j}^{x}}$, $\boldsymbol{Dx_{j}}$ y $\boldsymbol{Ex}$ se computan definiendo capas nn.Linear dentro de la función __init__ y propagando hacia delante la representación de entrada h y e a través de las capas lineales dentro de la función forward.

class GatedGCN_layer(nn.Module):

    def __init__(self, input_dim, output_dim):
        super().__init__()
        self.A = nn.Linear(input_dim, output_dim)
        self.B = nn.Linear(input_dim, output_dim)
        self.C = nn.Linear(input_dim, output_dim)
        self.D = nn.Linear(input_dim, output_dim)
        self.E = nn.Linear(input_dim, output_dim)
        self.bn_node_h = nn.BatchNorm1d(output_dim)
        self.bn_node_e = nn.BatchNorm1d(output_dim)

Segundo, computamos las representaciones de los ejes. Esto se hace desde la función message_func, que itera sobre todos los ejes y computa sus representaciones. Especificamente, la linea e_ij = edges.data['Ce'] + edges.src['Dh'] + edges.dst['Eh'] computa la (Eq. 7) vista anteriormente. La función message_func devuelve Bh_j (que es $\boldsymbol{Bx_{j}}$ de la (Ec. 5)) y e_ij (Ec. 7) a través del eje hasta el mailbox del nodo vecino.

def message_func(self, edges):
    Bh_j = edges.src['Bh']
    # e_ij = Ce_ij + Dhi + Ehj
    e_ij = edges.data['Ce'] + edges.src['Dh'] + edges.dst['Eh']
    edges.data['e'] = e_ij
    return {'Bh_j' : Bh_j, 'e_ij' : e_ij}

Tercero, la función reduce_func recopila los mensajes enviados por la funcion message_func. Después de recopilar los datos del nodo Ah y los datos enviados Bh_j e e_ij del mailbox, la linea h = Ah_i + torch.sum(sigma_ij * Bh_j, dim=1) / torch.sum(sigma_ij, dim=1) computa la representación oculta de cada nodo como se indica en (Ec. 5). Nótese que ésto solamente representa el término $(\boldsymbol{Ax} + \sum_{v_j→v}{\eta(\boldsymbol{e_{j}})\odot \boldsymbol{Bx_{j}}})$ sin la conexión residual $\texttt{ReLU}(\cdot)$.

def reduce_func(self, nodes):
    Ah_i = nodes.data['Ah']
    Bh_j = nodes.mailbox['Bh_j']
    e = nodes.mailbox['e_ij']
    # sigma_ij = sigmoid(e_ij)
    sigma_ij = torch.sigmoid(e)
    # hi = Ahi + sum_j eta_ij * Bhj
    h = Ah_i + torch.sum(sigma_ij * Bh_j, dim=1) / torch.sum(sigma_ij, dim=1)
    return {'h' : h}

Dentro de la función forward, habiendo llamado g.update_all, obtenemos los resultados de la convolución de grafos h and e, que representa los términos $(\boldsymbol{Ax} + \sum_{v_j→v}{\eta(\boldsymbol{e_{j}})\odot \boldsymbol{Bx_{j}}})$ de la (Eq.5) y $\boldsymbol{e_{j}}$ de la (Ec. 7) respectivamente. Después se aplica normalización por batch para poder entrenar la red de manera efectiva. Finalmente, aplicamos $\texttt{ReLU}(\cdot)$ y sumamos las conexiones residuales para obtener las representaciones ocultas de los nodos y ejes, que a la postre son retornadas por la función forward.

def forward(self, g, h, e, snorm_n, snorm_e):

    h_in = h # conexión residual
    e_in = e # conexión residual

    g.ndata['h']  = h
    g.ndata['Ah'] = self.A(h)
    g.ndata['Bh'] = self.B(h)
    g.ndata['Dh'] = self.D(h)
    g.ndata['Eh'] = self.E(h)
    g.edata['e']  = e
    g.edata['Ce'] = self.C(e)

    g.update_all(self.message_func, self.reduce_func)

    h = g.ndata['h'] # resultado de la convolución del grafo
    e = g.edata['e'] # resultado de la convolución del grafo

    h = h * snorm_n # normalizar activación con respecto al número de nodos del grafo
    e = e * snorm_e # normalizar activación con respecto al número de ejes del grafo

    h = self.bn_node_h(h) # normalización por batch
    e = self.bn_node_e(e) # normalización por batch

    h = torch.relu(h) # activación no linear
    e = torch.relu(e) # activación no linear

    h = h_in + h # conexión residual
    e = e_in + e # conexión residual

    return h, e

A continuación, definimos el módulo MLP_Layer, que contiene varias capas totalmente conectadas (FCN). Creamos una lista de capas totalmente conectadas y la mandamos hacia delante a través de la red.

Finalmente, definimos nuestro modelo GatedGCN que contiene las clases anteriormente mencionadas: GatedGCN_layer y MLP_layer. La definición de nuestro modelo (GatedGCN) se muestra a continuación.

 class GatedGCN(nn.Module):
    def __init__(self, input_dim, hidden_dim, output_dim, L):
        super().__init__()
        self.embedding_h = nn.Linear(input_dim, hidden_dim)
        self.embedding_e = nn.Linear(1, hidden_dim)
        self.GatedGCN_layers = nn.ModuleList([
            GatedGCN_layer(hidden_dim, hidden_dim) for _ in range(L)
        ])
        self.MLP_layer = MLP_layer(hidden_dim, output_dim)
    def forward(self, g, h, e, snorm_n, snorm_e):
        # embedding de entrada
        h = self.embedding_h(h)
        e = self.embedding_e(e)
        # capas convolucionales del grafo
        for GGCN_layer in self.GatedGCN_layers:
            h, e = GGCN_layer(g, h, e, snorm_n, snorm_e)
        # clasificador MLP
        g.ndata['h'] = h
        y = dgl.mean_nodes(g,'h')
        y = self.MLP_layer(y)
        return y

En nuestro constructor, definimos los embeddings para e y h (self.embedding_e y self.embedding_h), self.GatedGCN_layers, que es una lista (de tamaño $L$) del modelo definido anteriormente: GatedGCN_layer, y finalmente self.MLP_layer, que también se ha definido anteriormente. A continuación, utilizamos estas inicializaciones y simplemente enviamos hacia delante a través del modelo generamos la salida y.

Para entender mejor el modelo, inicializamos un objecto del modelo e imprimimos su contenido para una mejor visualización:

# instanciamos la red
model = GatedGCN(input_dim=1, hidden_dim=100, output_dim=8, L=2)
print(model)

La estructura principal del modelo se muestra a continuación:

GatedGCN(
  (embedding_h): Linear(in_features=1, out_features=100, bias=True)
  (embedding_e): Linear(in_features=1, out_features=100, bias=True)
  (GatedGCN_layers): ModuleList(
    (0): GatedGCN_layer(...)
    (1): GatedGCN_layer(... ))
  (MLP_layer): MLP_layer(
    (FC_layers): ModuleList(...))

Como es de esperar, tenemos dos capas de GatedGCN_layer (ya que L=2), seguidas por una capa MLP_layer que finalmente nos proporciona una salida de 8 valores.

Seguidamente, definimos nuestras funciones train y evaluate. En nuestra función train, tenemos nuestro código genérico que toma muestras de dataloader. A continuación, batch_graphs, batch_x, batch_e, batch_snorm_n y batch_snorm_e son alimentadas a nuestro modelo, que retorna batch_scores (de tamaño 8). Las puntuaciones predecidas son comparadas con los valores “ground truth” en nuestra función de pérdida: loss(batch_scores, batch_labels). Después, asignamos el valor cero a los gradientes (optimizer.zero_grad()), hacemos retropropagación (J.backward()) y actualizamos nuestros pesos (optimizer.step()). Finalmente, calculamos la pérdida por época y la precisión de entrenamiento. Utilizamos un código similar para nuestra función evaluate.

¡Finalmente estamos preparados para entrenar! Observamos que después de 40 épocas de entrenamiento, nuestro modelo ha aprendido a clasificar los grafos con una precisión de test del $87$%.