Grafo de Redes Convolucionales II

ConvNets de Grafo Espectral (GCN)

En la sección anterior discutimos la teoría espectral de grafos, una de las dos formas de definir la convolución para grafos, que ahora podemos usar para definir GCN Espectrales.

GCN Espectral Convencional

Definimos una capa convolucional espectral de grafo tal que dada la capa $h^l$, la activación de la siguiente capa es:

donde $\eta$ representa una activación no lineal y $w^l$ es un filtro espacial. El lado derecho de la ecuación es equivalente a $\eta(\hat{w}^l(\Delta)h^l)$ donde $\hat{w}^l$ representa un filtro espectral y $\Delta$ es el laplaciano. Podemos descomponer aún más el lado derecho de la ecuación en $\eta(\boldsymbol{\phi}\hat{w}^l(\Lambda)\boldsymbol{\phi^\top}h^l)$, donde $\boldsymbol{\phi}$ es la matriz de Fourier y $\Lambda$ son los valores característicos. Esto produce la ecuación de activación final como se muestra a continuación.

El objetivo es aprender el filtro espectral $\hat{w}^l(\lambda)$ usando retropropagación en lugar de la elaboración manual.

Esta técnica fue la primera técnica espectral utilizada para ConvNets, pero tiene algunas limitaciones:

• No hay garantía de localización espacial de filtros
• Es preciso aprender $O(n)$ parámetros por capa ($\hat{w}(\lambda_1)$a$\hat{w}(\lambda_n)$)
• La tasa de aprendizaje es $O(n^2$) porque $\boldsymbol{\phi}$ es una matriz densa

SplineGCNs

Las SplineGCN implican el cálculo de filtros espectrales suaves para obtener filtros espaciales localizados. La conexión entre la suavidad en el dominio de frecuencia y la localización en el espacio se basa en la identidad de Parseval (también relación de indeterminación de Heisenberg): derivada más pequeña del filtro espectral (función más suave) $\Leftrightarrow$ varianza más pequeña del filtro espacial (localización).

¿Cómo obtenemos un filtro espectral suave? Descomponemos el filtro espectral para que sea una combinación lineal de $K$ kernels suaves $\boldsymbol{B}$ (splines) de modo que $\hat{w}^l(\Lambda)=diag(\boldsymbol{B}w^l)$. La ecuación de activación es la siguiente.

Ahora, solo tenemos $O(1)$ parámetros ($K$ constantes) por capa para aprender a través de la retropropagación. Sin embargo, la complejidad del aprendizaje sigue siendo $O(n^2)$.

LapGCNs

¿Cómo aprendemos en tiempo lineal $O(n)$ (en relación al tamaño del grafo $n$)? La complejidad $O(n^2)$ es un resultado directo del uso de autovectores laplacianos. Necesitamos evitar la descomposición propia, que se puede lograr aprendiendo directamente una función del Laplaciano. La función espectral será un monomio del Laplaciano como se muestra aquí.

Una característica interesante es que los filtros están localizados exactamente en soportes de k-saltos

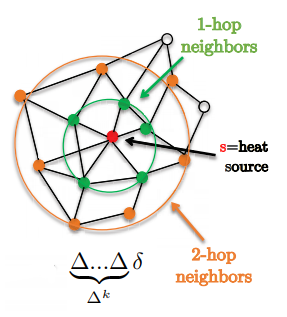
Figura 1: muestra vecindarios de 1 y 2 saltos </center> Reemplazamos la expresión $\Delta^kh$ con $X_k$, una ecuación recursiva definida como, $$ X_k=\Delta X_{k-1} \text{ and } X_0=h $$ La complejidad ahora es $O(E.K)=O(n)$ para grafos (del mundo real) dispersos. Podemos remodelar $X_k$ en $\bar{X}$ para formar una operación lineal. Ahora tenemos la siguiente ecuación de activación. $$ h^{l+1}=\eta\bigg(\sum^{K-1}_{k=0}w_kX_k\bigg)=\eta\Big((w^l)^\top \bar{X}\Big) $$ Nota: Dado que no se descompone espectralmente el Laplaciano, todas las operaciones están en el dominio espacial (no espectral), por lo que llamarlas GCN espectrales puede estar equivocado. Además, otro inconveniente de las LapGCN es que las capas convolucionales implican operaciones lineales dispersas, para las que los GPU no están completamente optimizados. Ahora hemos resuelto las 3 limitaciones de las GCN convencionales a través de filtros localizados (en soportes de $K$-saltos), $O(1)$ parámetros por capa y $O(n)$ complejidad de aprendizaje. Sin embargo, la limitación de LapGCN es que la base monomial ($\Delta^0, \Delta^1, \ldots$) utilizada es inestable para la optimización porque no es ortogonal (cambiar un coeficiente cambia la aproximación de la función). ### ChebNets Para resolver el problema de la base inestable, podemos usar cualquier base ortonormal, pero debe tener una ecuación recursiva para asegurar la complejidad lineal. Para ChebNets usamos polinomios de Chebyshev, y como en una LapGCN, representamos la expresión $T_k(\Delta)h$ (función de Chebyshev aplicada a $h$) por $X_k$, una ecuación recursiva definida como, $$ X_k=2\tilde{\Delta} X_{k-1} - X_{k-2}, X_0=h, X_1=\tilde{\Delta}h \text{ and } \tilde{\Delta} = 2\lambda_n^{-1}\Delta - \boldsymbol{I} $$ Ahora tenemos estabilidad bajo la perturbación del coeficiente. ChebNets son GCN que se pueden utilizar para cualquier dominio de grafo arbitrario, pero la limitación es que son isotrópicas. Las ConvNet estándar producen filtros *anisotrópicos* porque las cuadrículas euclidianas tienen dirección, mientras que los GCN espectrales calculan filtros *isotrópicos* ya que los grafos no tienen noción de dirección (arriba, abajo, izquierda, derecha). Podemos extender ChebNets a múltiples grafos usando un filtro espectral 2D. Esto puede ser útil, por ejemplo, en sistemas de recomendación donde tenemos grafos de películas y grafos de usuario. Las ChebNets de grafos múltiples tienen la siguiente ecuación de activación. $$ h^{l+1}=\eta(\hat{w}(\Delta_1,\Delta_2)*h^l) $$ ### CayleyNets Las ChebNets son inestables para producir filtros (localizar) con bandas de frecuencia de interés (comunidades de grafos). Para CayleyNets, en cambio, utilizamos como base ortonormal los racionales de Cayley. $$ \hat{w}(\Delta)=w_0+2\Re\left\{\sum^{K-1}_{k=0}w_k\frac{(z\Delta-i)^k}{(z\Delta+i)^k}\right\} $$ Las CayleyNets tienen las mismas propiedades que las ChebNets (son isotrópicas), pero están localizadas en frecuencia (con zoom espectral) y proporcionan una clase más rica de filtros (para el mismo orden $K$). ## [ConvNets de grafos espaciales] (https://www.youtube.com/watch?v=Iiv9R6BjxHM&list=PLLHTzKZzVU9eaEyErdV26ikyolxOsz6mq&index=24&t=3964s) ### Coincidencia de Modelos Para entender las ConvNets de grafos espaciales, volvemos a la definición de ConvNets de Coincidencia de Modelos. El problema principal cuando realizamos Coincidencia de Modelos para grafos es la falta de orden o posicionamiento de los nodos para el modelo. Todo lo que tenemos son los índices de los nodos, lo que no es suficiente para coincidir la información entre ellos. ¿Cómo diseñamos una coincidencia de modelos para que sea invariante a la re-parametrización del nodo? Es decir, si tenemos un grafo y uno de los nodos tiene un índice arbitrario, digamos 6, este índice también podría haber sido 122. Por lo tanto, es esencial poder realizar coincidencia de modelos independientemente del índice del nodo. La forma más sencilla de hacer esto es tener solo un vector modelo $w^l$, en lugar de tener $w_{j1}$, $w_{j2}$, $w_{j3}$ y así sucesivamente. Así que coincidimos este vector $w^l$ con todas las demás características de nuestro grafo. La mayoría de las redes neuronales de grafo actuales utilizan esta propiedad.
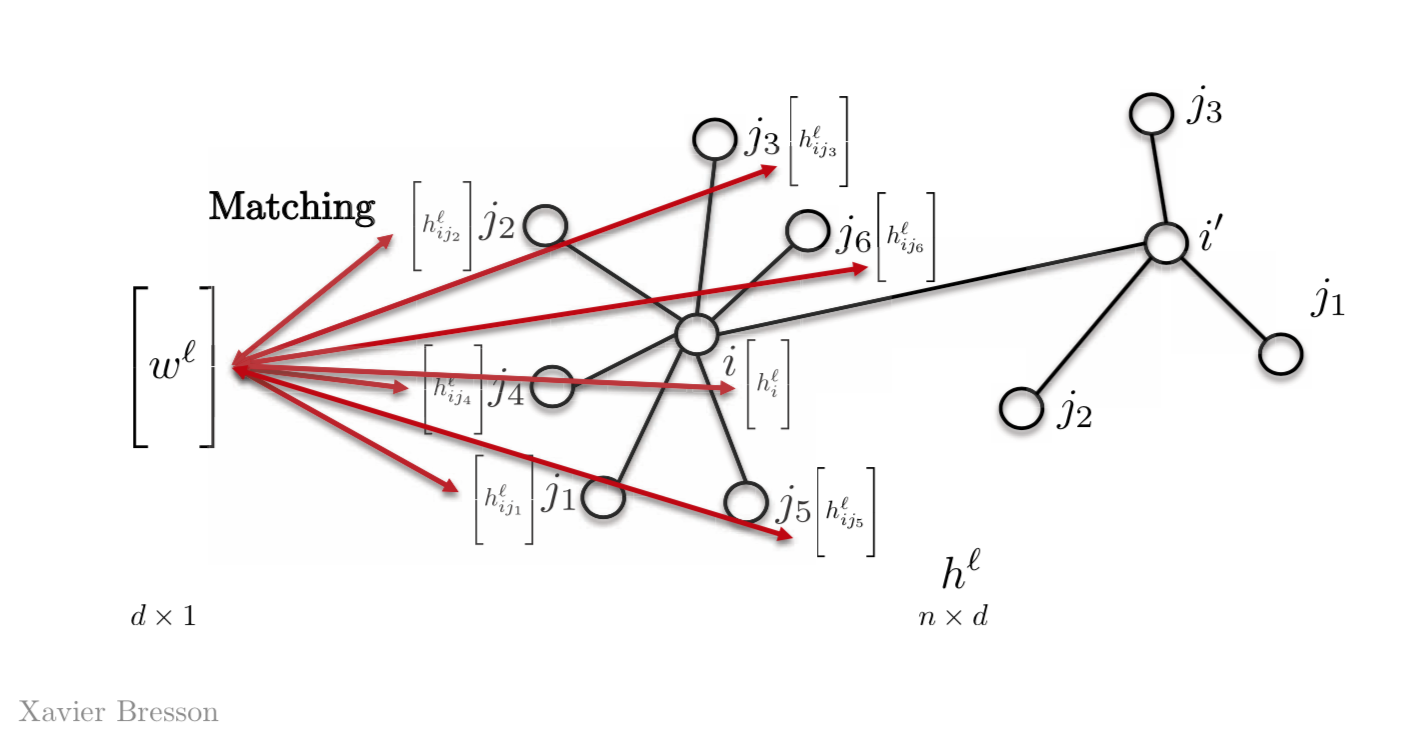
Figura 2: Coincidencia de Modelos usando un vector modelo Matemáticamente, para una característica tenemos, $$h_{i}^{l+1}=\eta\bigg(\sum_{j \in N_{i}} \langle w^l,h_{ij}^l \rangle \bigg)$$ donde, $w^l$ es el vector modelo en la capa $l$ de dimensiones $d \times 1$ y $h_{ij}^l$ es el vector en el nodo j con $d \times 1$ que resultará en una cantidad scalar $h_{i}^{l+1}$ en el nodo $i$. para obtener más ($d$) características, $$h_{i}^{l+1}=\eta\bigg(\sum_{j \in N_{i}} \boldsymbol{W}^l,h_{ij}^l\bigg)$$ donde, $\boldsymbol{W}^l$ tiene la dimensionalidad $d \times d$ y $h_ {i}^{l+1}$ es $d \times 1$ para una representación vectorial, $$h^{l+1}=\eta(\boldsymbol{A} h^l \boldsymbol{W}^l)$$ donde, $ \ boldsymbol {A} $ es la matriz de adyacencia de dimensiones $n \times n$, $h^l$ es la función de activación en la capa $l$ con dimensiones $n \times d$. En base a esta definición de coincidencia de modelos, podemos definir dos tipos de GCN espaciales: GCN isotrópicas y GCN anisotrópicas. ## GCN isotrópicas ### GCN espaciales convencionales Tiene la misma definición que antes, pero agregamos la matriz Diagonal a la ecuación, de tal manera que encontremos el valor medio de la vecindad. La representación matricial es, $$h^{l+1} = \eta(\boldsymbol{D}^{-1}\boldsymbol{A}h^{l}\boldsymbol{W}^{l})$$ donde, $\boldsymbol{A}$ tiene las dimensiones $n \times n$, $h^{l}$ tiene dimensiones $n \times d$ y $W^{l}$ tiene dimensiones $d \times d$, lo que da como resultado una matriz $n \times d$ $h^{l+1}$. Y la representación vectorial es, $$h_{i}^{l+1} = \eta\bigg(\frac{1}{d_{i}}\sum_{j \in N_{i}}\boldsymbol{A}_{ij}\boldsymbol{W}^{l}h_{j}^{l}\bigg)$$ donde, $h_{i}^{l+1}$ tiene las dimensiones de $d \times 1$ La representación vectorial es responsable de manejar la ausencia de ordenamiento de nodos, que es invariante a la re-parametrización de nodos. Es decir, agregando al ejemplo anterior, si el nodo tiene un índice 6 y se cambia a 122, esto no cambiará nada en el cálculo de la función de activación de la siguiente capa $ h ^ {l + 1} $. También podemos ocuparnos de vecindarios de diferentes tamaños. Es decir, podemos tener un vecindario de 4 o 10 nodos y no cambiaría nada. El campo de recepción local está dado por diseño. Es decir, con Redes de Grafo Neuronales solo tenemos que considerar los vecinos. Tenemos peso compartido. Es decir, tenemos la misma matriz $\boldsymbol{W}^{l}$ para todas las características sin importar la posición del grafo, lo cual es una propiedad de la convolución. Esta formulación también es independiente del tamaño del grafo, ya que todas las operaciones se realizan localmente. Dado que es un modelo isotrópico, los vecinos tendrán la misma matriz $\boldsymbol{W}^{l}$.
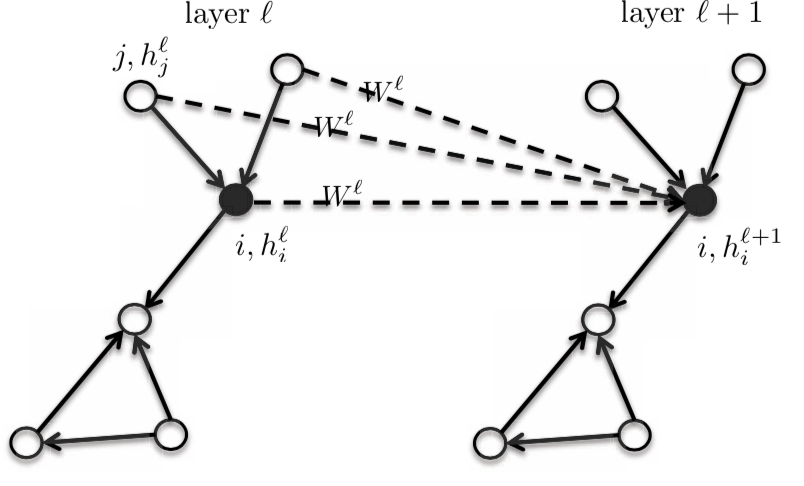
Figura 3: Modelo isotrópico $$h_{i}^{l+1} = f_\text{GCN}(h_{i}^{l}, \{h_{j}^l: j \rightarrow i\})$$ Entonces, la activación de la siguiente capa $h_{i}^{l+1}$ es una función de la activación de la capa anterior $h_{i}^{l}$ en el nodo $i$ y la vecindad de $i$. Cuando cambiamos la función, obtenemos una familia completa de grafos. ### ChebNets y GCN espaciales convencionales La GCN espacial convencional definida anteriormente es una simplificación de ChebNets. Podemos truncar la expansión de ChebNet usando las dos primeras funciones de Chebyshev para terminar con, $$h_{i}^{l+1} = \eta\bigg(\frac{1}{\hat{d_{i}}}\sum_{j \in N_{i}}\hat{\boldsymbol{A}_{ij}}\boldsymbol{W}^{l}h_{j}^{l}\bigg)$$ ### GraphSage Si la matriz de adyacencia $\boldsymbol{A}_{ij} = 1$ para los bordes en las GCN espaciales simples, obtenemos, $$h_{i}^{l+1} = \eta\bigg(\frac{1}{d_{i}}\sum_{j \in N_{i}}\boldsymbol{W}^{l}h_{j}^{l}\bigg)$$ Para esta ecuación, le damos al vértice central/de núcleo $i$ y a su vecindario el mismo modelo de peso $\boldsymbol{W}^{l}$. Podemos diferenciar esto dando al nodo central $\boldsymbol{W}\_{1}^{l}$, y teniendo un modelo de nodo diferente $\boldsymbol{W}_{2}^{l}$ para el Vecindario one-hot. Esto mejorará considerablemente el rendimiento de las GNNes. Esta red todavía se considera de naturaleza isotrópica, ya que los vecinos tienen el mismo peso. $$h_{i}^{l+1} = \eta\bigg(\boldsymbol{W}_{1}^{l} h_{i}^{l} + \frac{1}{d_{i}} \sum_{j \in N_{i}} \boldsymbol{W}_{2}^{l} h_{j}^{l}\bigg)$$ donde, $\boldsymbol{W}\_{1}^{l}$ y $\boldsymbol{W}\_{2}^{l}$ son de dimensión $d \times d$; $h_{i}^{l}$ y $h_{j}^{l}$ son de la dimensión $d \times 1$. En esta ecuación, podemos encontrar la suma o el máximo de $\boldsymbol{W}\_{2}^{l} h_{j}^{l}$ o la memoria a corto y largo plazo de $h_{j}^{l}$, en lugar de la media.
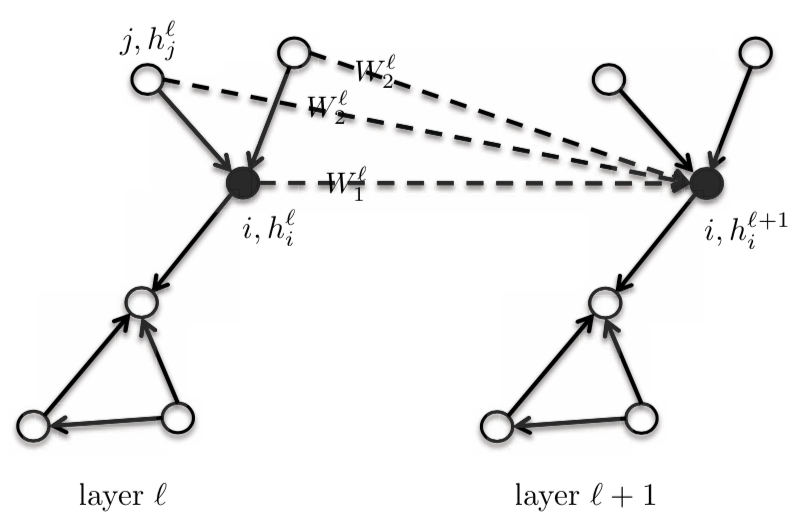
Figura 4: GraphSage ### Redes de isomorfismos de grafos (GIN) Una arquitectura que puede diferenciar grafos que no son isomorfos. *Isomorfismo* es la medida de equivalencia entre grafos. En la siguiente figura, los dos grafos son considerados isomórficos entre sí. Los grafos isomórficos se tratarán de manera similar y los grafos no isomórficos se tratarán de manera diferente. GIN es una GCN isotrópica. $$h_{i}^{l+1} = \texttt{ReLU}(\boldsymbol{W}_{2}^{l}\space \texttt{ReLU}(\texttt{BN}(\boldsymbol{W}_{1}^{l} \hat(h_{j}^{l+1})))$$ donde, $\texttt{BN}$ significa Normalización por Batch. $$h_{i}^{l+1} = (1 + \epsilon)h_{i}^{l} + \sum_{j \in N_{i}} h_{j}^{l}$$
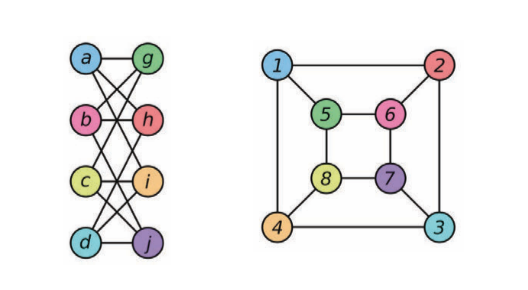
Figura 5: Ejemplos de dos grafos isomorfos ## [GCN anisotrópicas] (https://www.youtube.com/watch?v=Iiv9R6BjxHM&list=PLLHTzKZzVU9eaEyErdV26ikyolxOsz6mq&index=24&t=5586s) Las CNN estándar tienen la capacidad de producir filtros anisotrópicos, algunos que favorecen ciertas direcciones. Esto se debe a que la estructura direccional se basa en arriba, abajo, izquierda y derecha. Sin embargo, las GCN descritas anteriormente no tienen noción de dirección y, por lo tanto, solo pueden producir filtros isotrópicos. La anisotropía se puede introducir de forma natural, con características de borde. Por ejemplo, las moléculas pueden tener enlaces simples, dobles y triples. Gráficamente, se introduce ponderando diferentes vecinos de forma diferente. ### MoNets MoNets usan el grado del grafo para aprender los parámetros de un modelo de mezcla gaussiana (GMM).
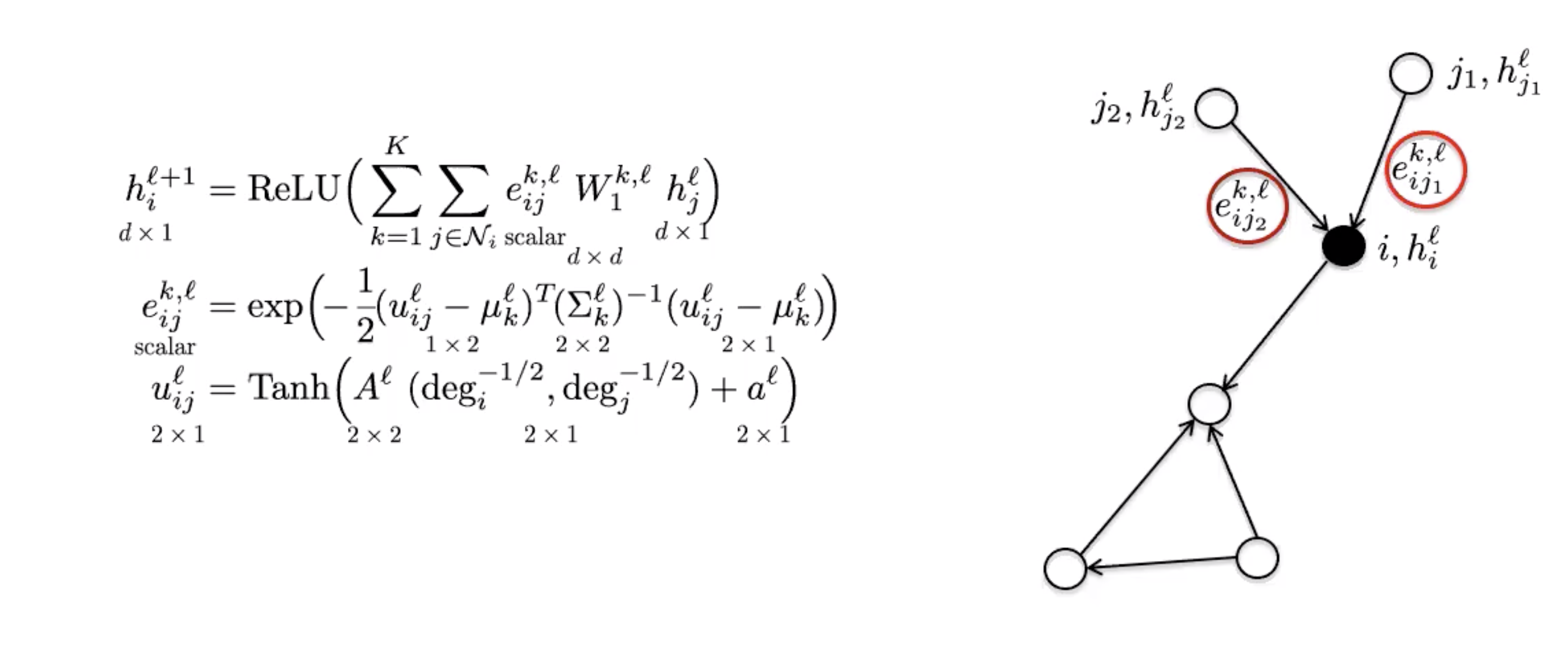
Figura 6: MoNet ### Redes de grafos de atención (GAT) GAT utiliza el mecanismo de atención para introducir anisotropía en la función de agregación de vecindad.
Figura 7: GAT ### ConvNets de grafos cerrados Estas utilizan un mecanismo de cerrado de borde simple, que puede verse como un proceso de atención más suave como el mecanismo de atención escasa que se usa en las GAT.
Figura 8: ConvNet de gráfico cerrado ### Transformadores de grafo
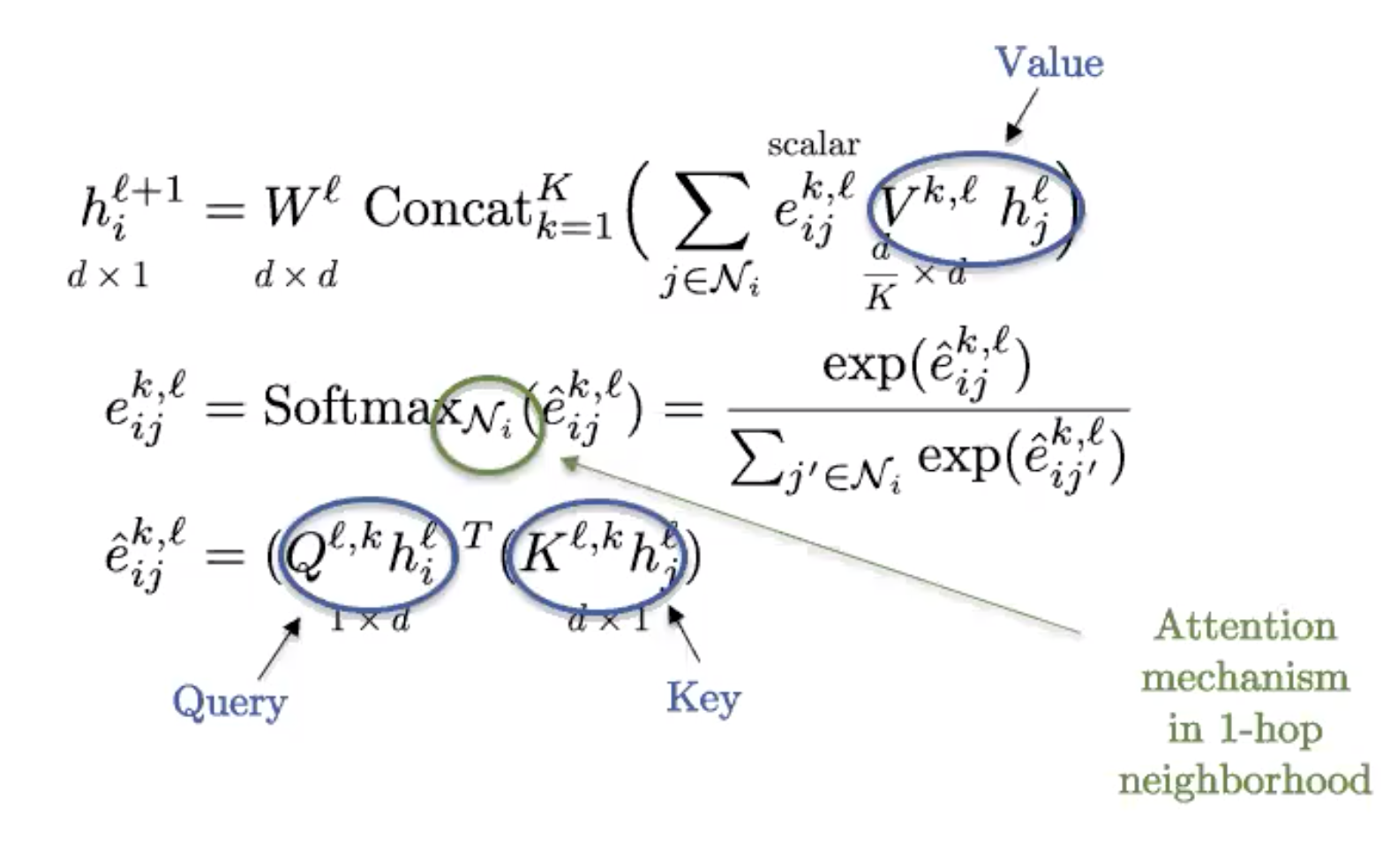
Figura 9: Transformadores de grafo Esta es la versión del transformador de grafo estándar, comúnmente utilizado en PNL. Si el grafo está completamente conectado (cada dos nodos comparten un borde), recuperamos la definición de un transformador estándar. Los grafos obtienen su estructura de la dispersidad, por lo que el grafo completamente conectado tiene una estructura trivial y es esencialmente un conjunto. Los transformadores se pueden ver como Redes Neuronales **Conjunto** y, de hecho, son la mejor técnica actualmente para analizar conjuntos/bolsas de características. ## Evaluación Comparativa de las GNN Los puntos de referencia son una parte esencial del progreso en cualquier campo. El punto de referencia recientemente publicado [Benchmarking Graph Neural Networks](https://arxiv.org/pdf/2003.00982.pdf/) tiene seis conjuntos de datos de media escala que se pueden usar para cuatro problemas fundamentales de grafos: clasificación de grafos, regresión de grafos, clasificación de nodos y clasificación de bordes. Aunque estos conjuntos de datos son de tamaño mediano, son suficientes para separar estadísticamente las tendencias en varias GNNes. Como ejemplo de una **Tarea de Regresión de Grafo**, querríamos predecir la solubilidad molecular.
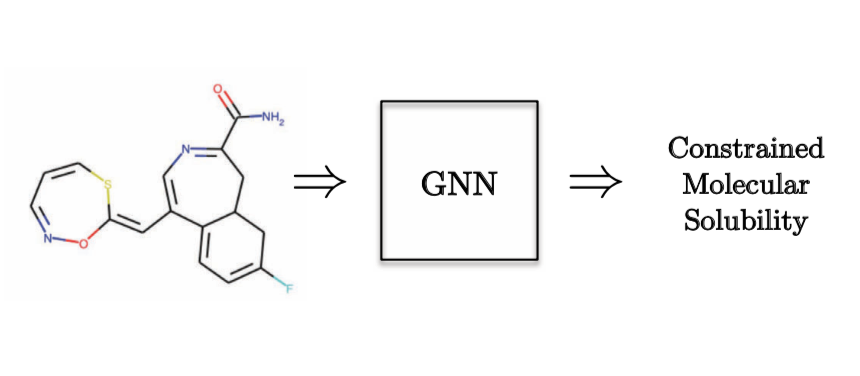
Figura 10: Tarea de Regresión de Grafo - Química cuántica
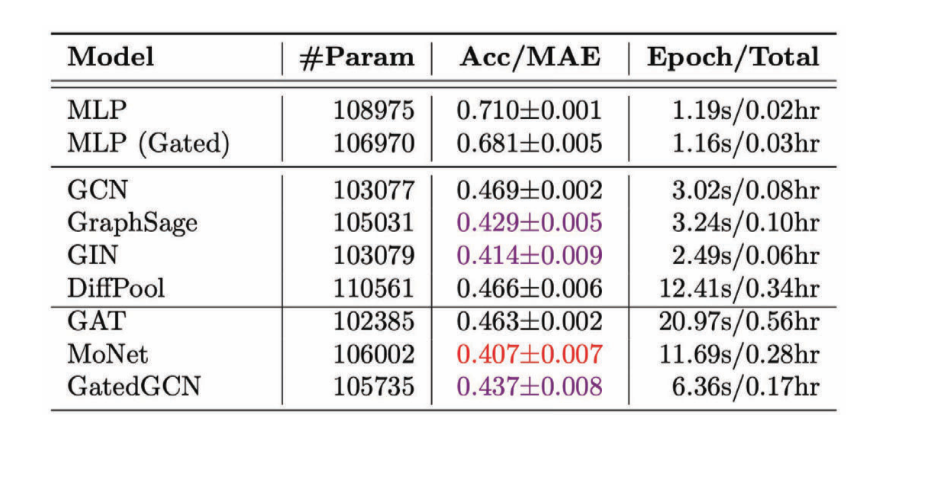
Figura 11: Performance de varias GCN en la tarea de regresión Observamos que en la mayoría de los casos las GCN anisotrópicos funcionan mejor en comparación con las GCN isotrópicas porque usamos propiedades direccionales. Para una **tarea de Clasificación de Grafo**, se eligió un problema de visión por computadora donde tenemos supernodos de imágenes y queremos clasificar la imagen.
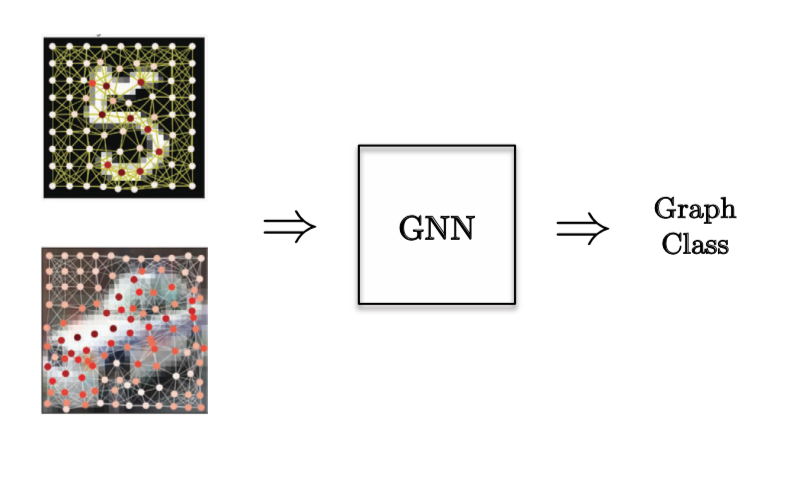
Figura 12: Tarea de Clasificación de Grafo
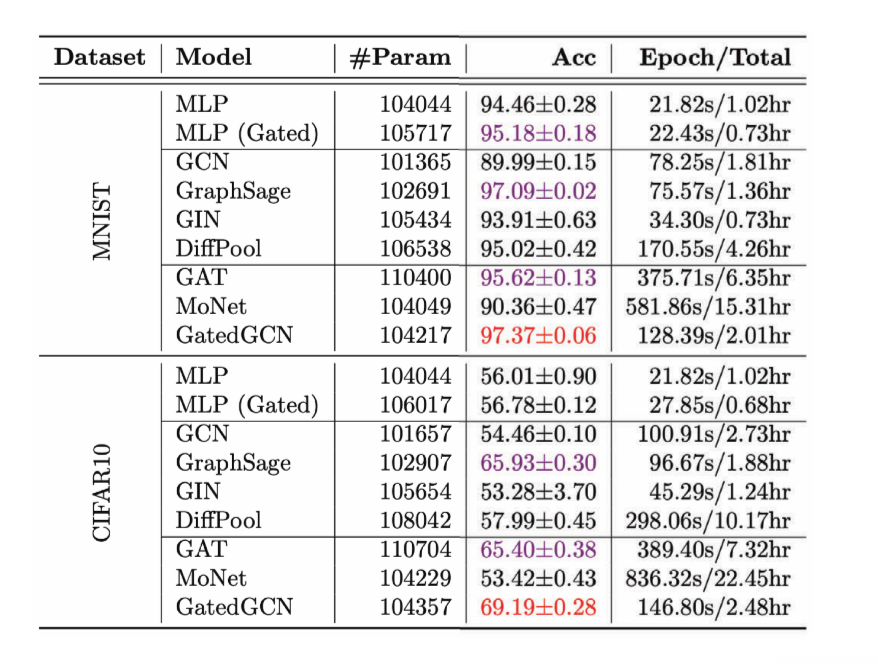
Figura 13: Performance de varias GCN en la tarea de Clasificación de Grafo Para una **Tarea de Clasificación de Bordes**, hemos considerado el problema de Optimización Combinatorial del problema del viajante (TSP por sus siglas en inglés), donde queremos saber si un borde en particular pertenece a la solución óptima. Si pertenece a la solución, cae en la clase 1, de lo contrario en la clase 0. Aquí necesitamos características de borde explícitas, y el único modelo que hace un buen trabajo es GatedGCN.
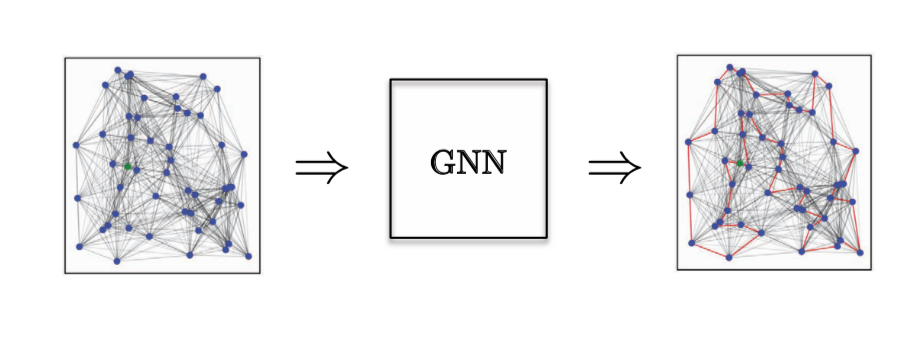
Figura 14: Tarea de clasificación de Bordes.
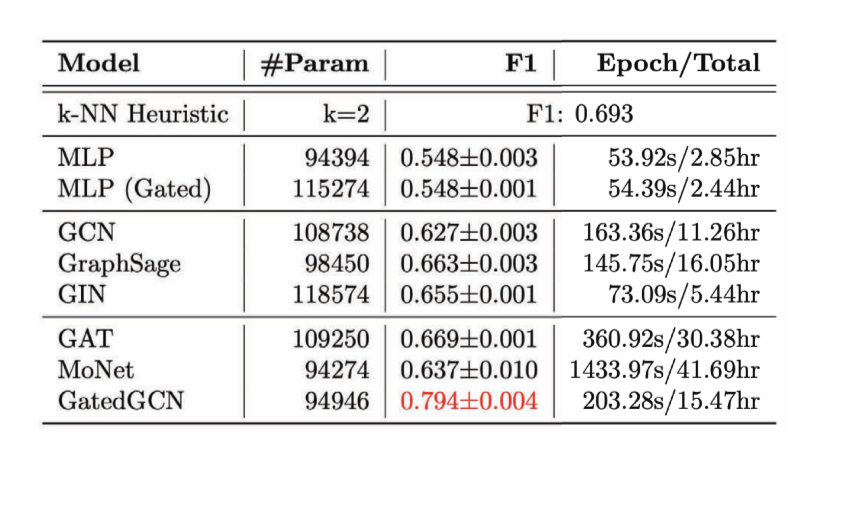
Figura 15: Performance de varias GCN en la Tarea de Clasificación de Bordes También podemos usar GCN para tareas auto-supervisadas, no se limitan a modelos de aprendizaje supervisados. Según el Dr. Yann LeCun, casi todas las tareas de aprendizaje auto-supervisadas explotan algún tipo de estructura de grafo. Cuando realizamos una tarea de aprendizaje auto-supervisado en texto, donde tomamos una secuencia de palabras y aprendemos a predecir palabras faltantes o nuevas oraciones. Aquí hay una estructura de grafo, que es la cantidad de veces que una palabra aparece a cierta distancia de otra palabra. El texto sería un grafo lineal y los vecinos elegidos se usarían para entrenar un Transformador. En el caso del entrenamiento contrastivo, donde tenemos dos muestras que son similares y dos que son diferentes, es esencialmente un grafo de similitud, donde dos muestras están vinculadas cuando son similares y si no están vinculadas se consideran diferentes. ## Conclusión Las GCN generalizan las CNN a datos en grafos. El operador de convolución necesitaba ser rediseñado para grafos. Hacer esto para la coincidencia de modelos dio lugar a GCN espaciales, y para la convolución espectral condujo a GCN espectrales. Existe una complejidad lineal para los grafos dispersos y la implementación de GPU, aunque esta última aún no está optimizada para la multiplicación de matrices dispersas. Las aplicaciones abundan como se muestra a continuación.
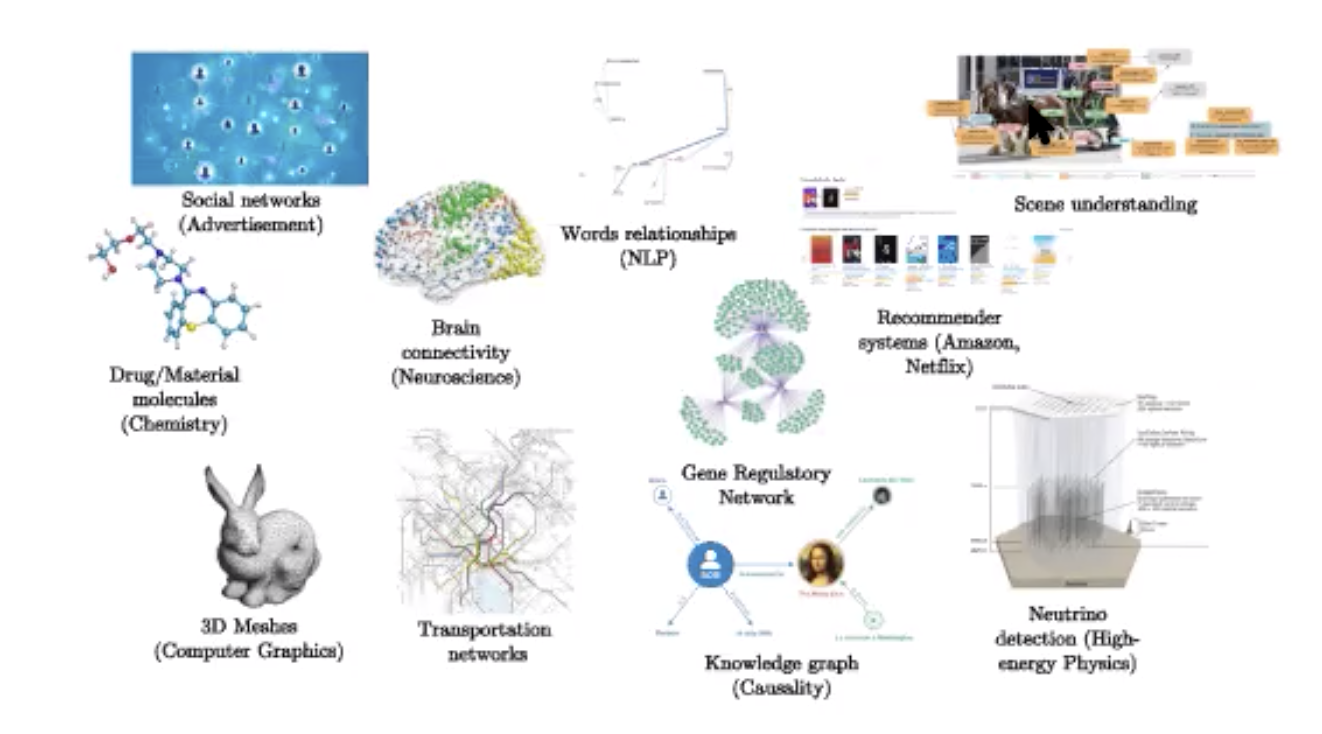
Figura 16: Aplicaciones