Grafo de Redes Convolucionales I

🎙️ Xavier Bresson

Redes Convolucionales Tradicionales

Las redes convolucionales son arquitecturas poderosas que permiten resolver problemas de aprendizaje de alta dimensionalidad.

${10}^{1,000,000}$ points

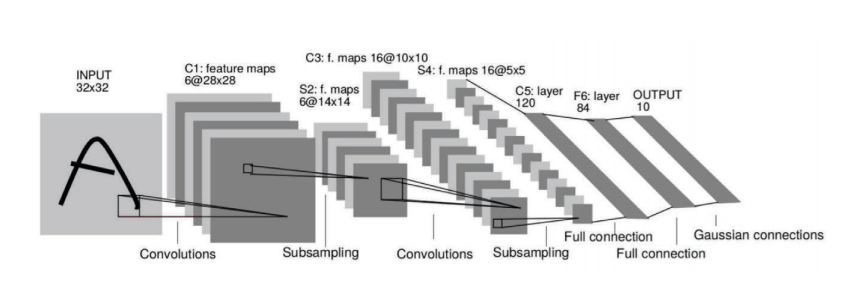
Fig. 1: ConvNets extract representation of high-dimensional image data.

–>

¿Cuál es la maldición de la dimensionalidad?

Supongamos que tenemos una imagen de 1024 x 1024 pixeles. Esta imagen se puede ver como un punto en un espacio de 1,000,000 de dimensiones. Utilizando 10 muestras por dimensión genera ${10}^{1,000,000}$ imágenes, lo cual es muy grande. Las redes convolucionales son extremadamente poderosas para extraer la mejor representación de datos de alta dimensionalidad, similar a la de este ejemplo.

• dim(image) = 1024 x 1024 = ${10}^{6}$
• Para N = 10 muestras/dim –> ${10}^{1,000,000}$ puntos

Fig. 1: Las redes convolucionales extraen representaciones de datos de imágenes de alta dimensionalidad.

Principales supuestos sobre Redes Convolucionales:

1. Datos (imágenes, videos, habla) son composicionales.

Están formados por patrones que son:

• Locales Una neurona en una red neuronal sólo está conectada a capas adyacentes, pero no a todas las capas de la red. A esto le llamamos el supuesto del campo receptivo local.
• Estacionarios Tenemos algunos patrones que son similares y que son compartidos en el dominio de nuestra imagen. Por ejemplo, la sábana amarilla en el centro de la imagen de la figura 2.
• Jerárquica Los atributos (features) de nivel bajo se van a combinar para formar rasgos de nivel intermedio. Subsecuentemente, estos atributos de nivel intermedio se combinarán progresivamente para formar rasgos de mayor y mayor nivel. Por ejemplo, una representación visual.

Fig. 2: Los datos son composicionales.

2. Las redes convolucionales aprovechan la estructura composicional

Las redes extraen los atributos composicionales y se los proporciona al clasificador, recomendador, etc.

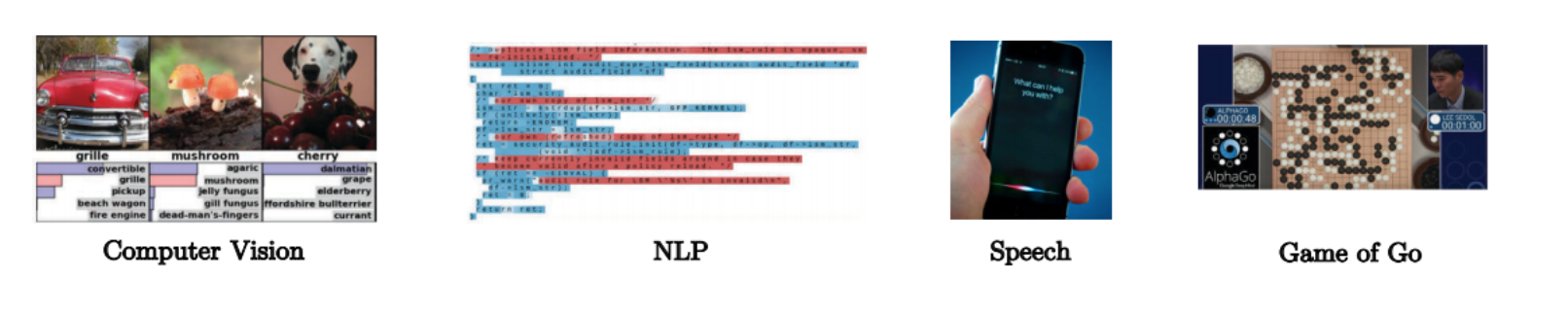
Fig. 3: Las redes convolucionales aprovechan la estructura composicional.

Dominio de grafo

Dominio de los datos

• Imágenes, volúmenes, videos se basan en dominios Euclideanos de 2D, 3D y 2D+1 (cuadrículas). Cada pixel es representado por un vector de valores de rojo, verde y azul.

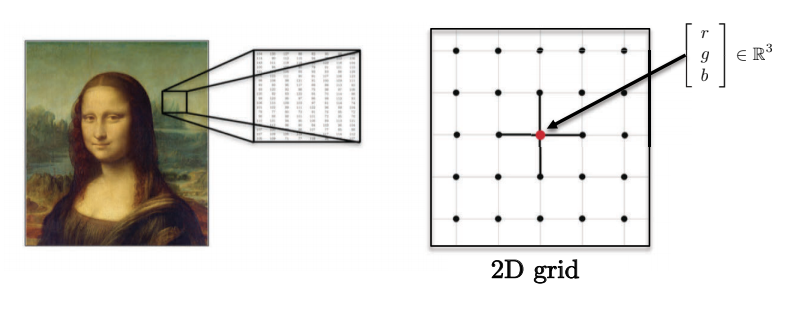
Fig. 4: Las imágenes pueden tener múltiples dimensiones

• Oraciones, palabras, y el habla se basan en dominios Euclideanos de 1D. Por ejemplo, cada caracter se puede representar por un número entero.

  
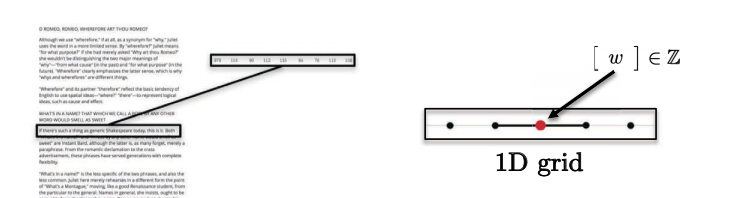
  Fig. 5: Secuencias sólo tienen una dimensión.

• Estos dominios tienen fuertes estructuras espaciales regulares, las cuales permiten que todas las operaciones de las redes convolucionales sean rápidas y bien definidas.

  
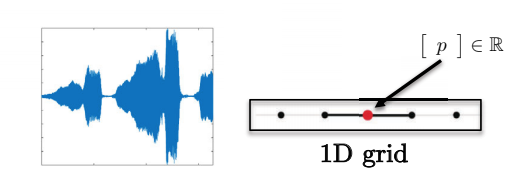
  Fig. 6: Datos del habla tienen una cuadrícula de 1D.

Dominio de grafos

Ejemplos motivacionales de los dominios de grafos

Consideremos una red social. La res social es capturada de mejor manera por un representación gráfica ya que las conexiones pareadas entre dos usuarios no forman una cuadrícula. Los nodos de estos grafos representan usuarios, mientras que los bordes entre nodos representan conexiones entre dos nodos (usuarios). Cada usuario tiene una matriz de atributos tridimensionales que contiene tales mensajes, imágenes y videos.

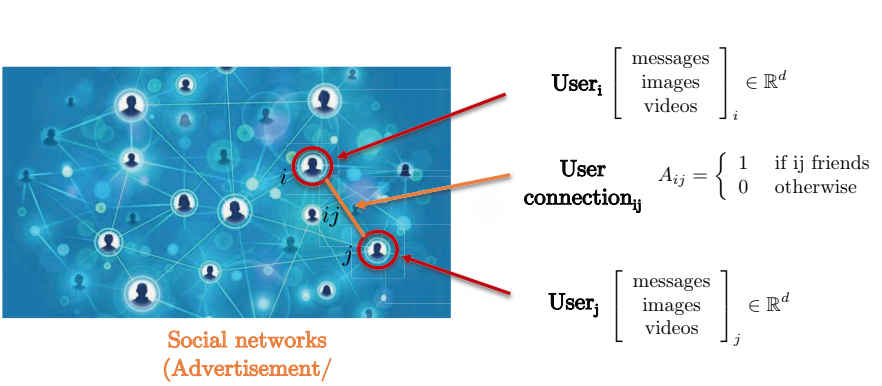
Fig. 7: Redes sociales representadas como grafos

La conexión entre la estructura y función de un cerebro para predecir enfermedades genéticas neuronales ofrece un ejemplo motivacional a considerar. Como se puede ver abajo, el cerebro está compuesto de varias regiones de interés (ROI). Estas ROIs están localmente conectadas a ciertas regiones de interés circundantes. La matriz de adyacencia representa el grado de fuerza entre diferentes regiones de interés.

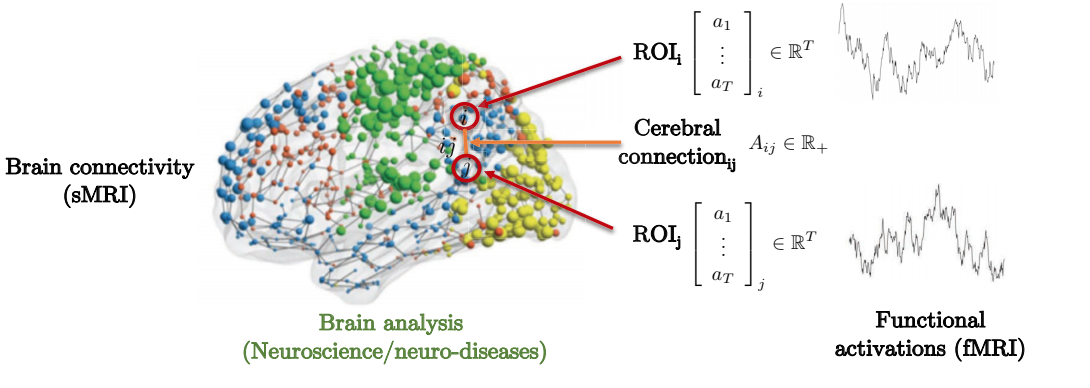
Fig. 8: Conectividad de un cerebro representada como grafo.

La química quántica también ofrece una interesante representación del dominio gráfico. Cada átomo es representado por un nodo en un grafo, la cual está conectada a otros átomos mediante enlaces utilizando bordes. Cada una de estas moléculas / átomos tienen distintos atributos, tales como una carga asociada, tipo de enlace, etc.

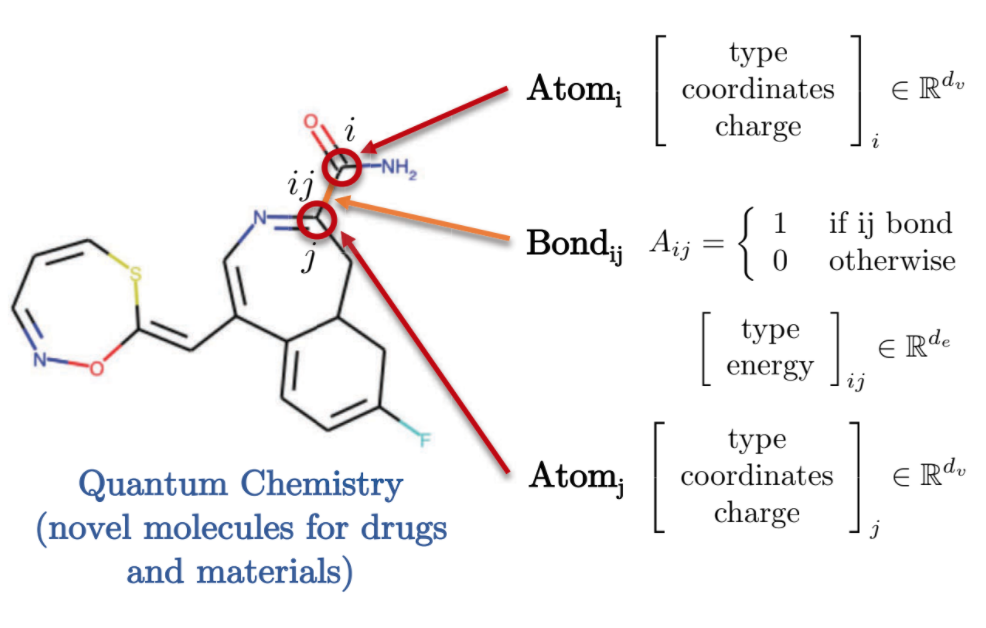
Fig. 9: Representación de química cuántica en un grafo.

Características y definición de grafos

• El grafo G es definido por: * Vértices V * Bordes E * Matriz de adyacencia A

• Atributos del grafo: * Atributos del nodo: $h_{i}$, $h_{j}$ (tipo de átomo) * Atributos del borde: $e_{ij}$ (tipo de enlace) * Atributos del gráfo: g (energía de molécula)

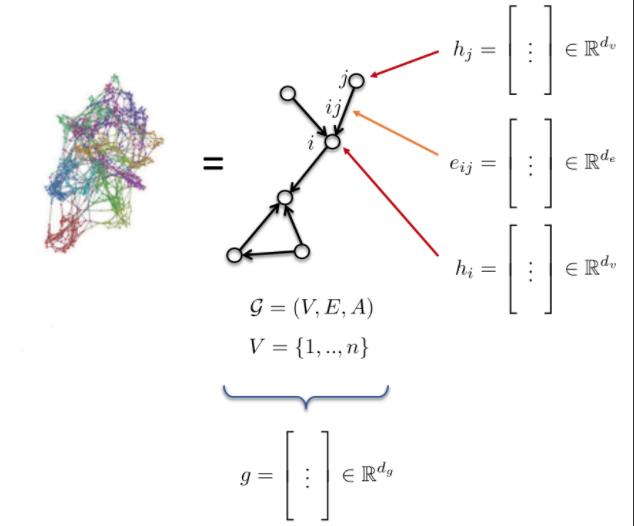
Fig. 10: Grafo.

Convolución de Redes Convolucionales Tradicionales

Convolución

Definimos, de manera abstracta, una convolución como:

\(h^{\ell+l} = w^\ell * h^\ell,\) donde $h^{\ell+1}$ es $n_1\times n_2\times d$-dimensional, $w^\ell$ es $3\times 3\times d$-dimensional, y $h^\ell$ es $n_1\times n_2\times d$-dimensional. Por ejemplo, $n_1$ y $n_2$ podría ser el número de pixeles en los ejes $x$ y $y$ de una imagen, respectivamente, y $d$ es la dimensionalidad de cada pixel (e.g., 3 para una imagen a color).
De esta manera, $h^{\ell+1}$ es un atribute en el $(\ell+1)$-ésima capa oculta obtenida al realizar la convolución $w^\ell$ a un atributo en la $\ell$-ésima capa.
Usualmente, el kernel es pequeño y representa un campo receptivo local – $3\times 3$ en este caso, o $5\times 5$, por ejemplo.
Nota: Las imágenes se rellenan (padding) para asegurarnos que las dimensiones de $h^{\ell+1}$ son iguales a las de $h^\ell$.\

Por ejemplo, en esta imagen el núcleo (kernel) puede ser utilizado para reconocer líneas

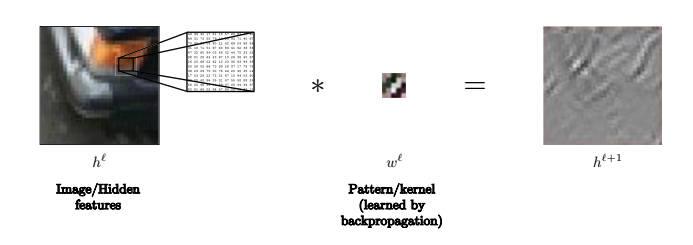
Fig. 11: El kernel se puede utilizar para reconocer líneas en imágenes.

¿Cómo definimos una convolución?

De manera más exacta, una convolución se define como:

\[h_i^{\ell+1} = w^\ell * h_i^\ell\] \[= \sum_{j\in\Omega}\langle w_j^\ell, h_{i-j}^\ell\rangle\] \[= \sum_{j\in\mathcal{N}_i} \langle w_j^\ell, h_{ij}^\ell\rangle\] \[=\sum_{j\in\mathcal{N}_i} \langle \Bigg[w_j^\ell\Bigg], \Bigg[h_{ij}\Bigg]\rangle\]

Lo anterior define una convolución como una correspondencia entre modelos (template matching).
Nosotros usualmente utilizamos $h_{i+j}$ en lugar de $h_{i-j}$, porque esta última, de hecho, es una correlación, que es más similar a una correspondencia entre modelos.

Sin embargo, realmente no importa si se utiliza la primera o segunda variable, ya que el kernel sólo está volteado, por lo tanto, no influye en el aprendizaje.

En la tercer linea, sólo escribimos $h_{i+j}^\ell$ como $h_{ij}^\ell$.

El kernel es muy pequeño, así que en lugar de sumar sobre toda la imagen $\Omega$, como en la segunda línea, de hecho, sólo sumamos sobre el vecindario de una celda $i$, $\mathcal{N}_i$, como se muestra en la tercera línea

Esto hace que la complejidad de una convolución sea $O(n)$, donde $n$ es el número de pixeles en una imágen de entrada.

Una convolución es exactamente, para cada $n$ pixeles, sumar sobre los productos internos de vectores de dimensión $d$ sobre $3\times 3$ cuadrículas.

La complejidad es entonces, $n\cdot 3\cdot 3\cdot d$, lo cual es $O(n)$; mas aún, esto se puede realizar en paralelo utilizando GPUs en cada uno de los $n$ pixeles.

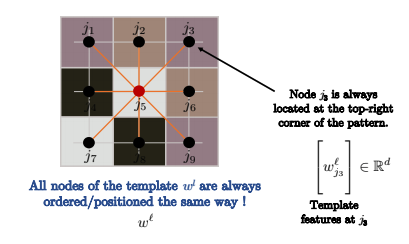
Fig. 12: Los nodos se ordenan de la misma manera.

Si el grafo sobre el que se está realizando la convolución es una cuadrícula, tal cual como en las convoluciones estándar en imágenes utilizadas en visión computacional, entonces los nodos se ordenan igual que en la imagen anterior. Entonces, $j_3$ siempre va a estar en la esquina superior derecha del patrón.

Así que para todos los nodos $i$ en la imagen que se encuentra abajo, como $i$ y $i’$, el orden de los nodos en el kernel siempre es el mismo. Por ejemplo, siempre que compares $j_3$ en la esquina superior derecha del patrón con la esquina superior de una parte de la imagen (lo que convolucionamos para cada pixel $i$), como se muestra abajo. Poniéndolo en términos matemáticos:

\[\langle\Bigg[w_{j_3}^\ell\Bigg], \Bigg[h_{ij_3}^\ell \Bigg]\rangle\]

y

\[\langle\Bigg[w_{j_3}^\ell\Bigg], \Bigg[h_{i'j_3}^\ell \Bigg]\rangle\]

siempre están en la esquina superior derecha entre el modelo y los parches de una imagen.

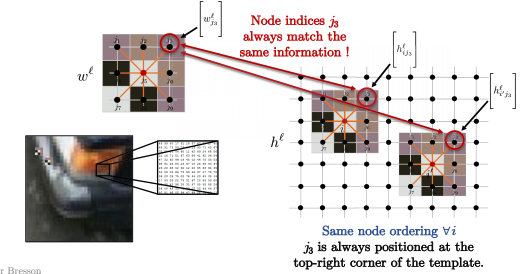
Fig. 13: Parches de una imagen que coinciden con los modelos.

¿Podemos extender la coincidencia de modelos para gráficas?

Tenemos un par de problemas:

1. Primero, en un grafo, no existe un orden de los nodos.

Así que en el modelo que se muestra abajo, el nodo $j_3$ no tiene una posición específica, pero sólo un índice (arbitrario). De tal manera, cuando tratamos de coincidir los nodos $i$ y $i’$ en la grafo de abajo, no sabemos si $j_3$ coincide con los mismos nodos en las dos convoluciones.
Esto es porque no existe una noción de la esquina superior derecha del grafo.
No existe una noción de arriba, abajo, izquierda o derecha.
Por lo tanto, la coincidencia de modelos no tiene un significado y no podemos utilizar la definicion de coincidencia de modelos directamente, como arriba.

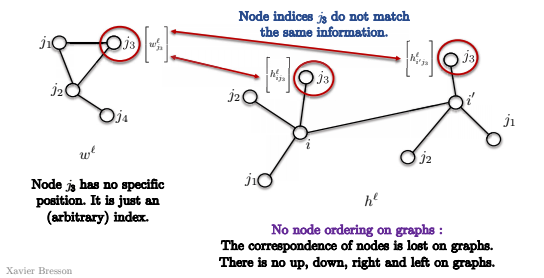
Fig. 14: No existe un orden de los nodos en un grafo.

1. El segundo problema es que los tamaños de vecindario pueden ser distintos.

De tal manera, cuanto el modelo $w^\ell$ que se muestra abajo tiene 4 nodos, pero el nodo $i$ tiene 7 nodos en su vecindario. ¿Cómo podemos comparar estos dos?

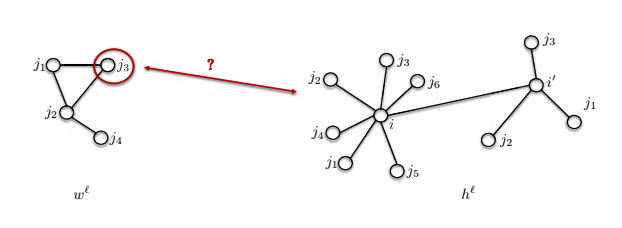
Fig. 15: Diferentes tamaños de vecidanrios en un grafo.

Convolución de grafos

Ahora utilizamos el Teorema de la Convolución para definir una convolución para gráficas.

El Teorema de la Convolución establece que una transformada de Fourier de una convolución de dos funciones es el producto punto de sus transformadas de Fourier:

\[\mathcal{F}(w*h) = \mathcal{F}(w) \odot \mathcal{F}(h) \implies w * h = \mathcal{F}^{-1}(\mathcal{F}(w)\odot\mathcal{F}(h))\]

En general, la transformada de Fourier tiene complejidad $O(n^2)$, pero si el dominio es una cuadrícula, entonces la complejidad puede ser reducida a $O(n\log n)$ con una transformada rápida de Fourier (FFT).

¿Podemos ampliar el Teorema de la Convolución a las gráficas?

Esto genera dos preguntas:

1. ¿Cómo de define una transformada de Fourier para gráficas?
2. ¿Cómo se calculan las convoluciones espectrales rápidas en un tiempo $O(n)$ para kernels compactos (así como en la coincidencia de modelos)?

\[w *_{\mathcal{G}} h \stackrel{?}{=} \mathcal{F}^{-1}_{\mathcal{G}}(\mathcal{F}_{\mathcal{G}}(w)\odot\mathcal{F}_{\mathcal{G}}(h))\]

Vamos a utilizar estos dos diseños para redes neuronales gráficas: La coincidencia de modelos será utilizada para redes convolucionales gráficas espaciales, mientras que el Teorema de la Convolución va a ser utilizado en redes convolucionales espectrales.

Grafo espectral de Redes convolucionales

¿Cómo realizar una convolución espectral?

Paso 1: Grafo Laplaciano

Esto es un operador central en la teoría de grafos espectral.

Define

\[\begin{aligned} \mathcal{G}=(V, E, A) & \rightarrow \underset{n \times n}{\Delta}=\mathrm{I}-D^{-1 / 2} A D^{-1 / 2} \\ & \quad \text { where } \underset{n \times n} D=\operatorname{diag}\left(\sum_{j \neq i} A_{i j}\right) \end{aligned}\]

Cabe destacar que la matriz $A$ es una matriz de adyacencia, y que $\Delta$ es la Laplaciana, la cual equivale la identidad menos la matriz de adyacencia normalizada por la matriz $D$. $D$ es una matriz diagonal y cada elemento en la diagonal es el grado del nodo. A esto se le llama una normalización Laplaciana o simplemente Laplaciana en este contexto.

La Laplaciana se interpreta como una medida de la suavidad del grafo, en otras palabras, la diferencia entre el valor local $h_i$ y el valor promedio de su vecindario de $h_j$’s. $d_i$ en la fórmula presentada abajo es el grado del nodo $i$, y $\mathcal{N}_{i}$ representa a todos los vecinos del nodo $i$.

\[(\Delta h)_{i}=h_{i}-\frac{1}{d_{i}} \sum_{j \in \mathcal{N}_{i}} A_{i j} h_{j}\]

La formula anterior muestra cómo aplicar la Laplaciana a a una función $h$ en el nodo %i$, el cual es de valor $h_i$ menos el valor promedio sobre los nodos de su vecindario $h_j$’s. Básicamente, si la señal es muy suave, el valor Laplaciano es pequeño y viceversa.

Paso 2: Funciones de Fourier

Las siguientes fórmulas indican la descomposición en eigenvalores de un grafo Laplaciano

\[\underset{n \times n}{\Delta}=\Phi^{T} \Lambda \Phi\]

La Laplaciana se factoriza en tres matrices, $\Phi ^ T$, $\Lambda$, $\Phi$.

$\Phi$ es definida abajo, ésta contiene vectores en columnas, o eigenvectores (Lap eigenvectors) de $\phi_1$ a $\phi_n$, cada uno de tamaño $n \times 1$, y a esos también se les llama funciones de Fourier. Y las funciones de Fourier forman una base ortonormal.

\[\begin{array}{l}\text { where } \underset{n \times n}{\Delta}\Phi=\left[\phi_{1}, \ldots, \phi_{n}\right]=\text { and } \Phi^{T} \Phi=\mathrm{I},\left\langle\phi_{k}, \phi_{k^{\prime}}\right\rangle=\delta_{k k^{\prime}} \\\end{array}\]

$\Lambda$ es la matriz diagonal con eigenvalores Laplacianos, y en la diagonal están $\lambda_1$ a $\lambda_n$. Y a partir de las normalizaciones, estos valores típicamente se encuentran en el intervalo de $0$ a $2$. A estos también se les conoce como el Espectro de un grafo. Ver la fórmula de abajo.

\[\begin{array}{c}\text { where } \underset{n \times n}\Lambda=\operatorname{diag}\left(\lambda_{1}, \ldots, \lambda_{n}\right) \text { and } 0 \leq \lambda_{1} \leq \ldots \leq \lambda_{n}=\lambda_{\max } \leq 2\end{array}\]

Abajo se puede ver un ejemplo de una revisión de la descomposición en eigenvalores. La matriz Laplaciana $\Lambda$ se multiplica por un eigenvector $\phi_k$, las dimensiones del resultado es $n \times 1$, y el resultado es $\lambda_k \phi_k$.

\[\begin{array}{ll}\text { and } \underset{n \times 1}{\Delta \phi_{k}}=\lambda_{k} \phi_{k}, & k=1, \ldots, n \\ & \end{array}\]

La imagen de abajo muestra una visualización de los eigenvectores de una matriz Laplaciana Euclideana de 1D.

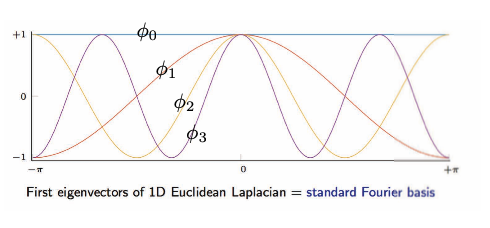
Fig. 16: Dominio de Cuadrícula / Euclideana: eigenvectores de una Laplaciana Euclideana de 1D.

Para el dominio de grafos, de izquierda a derecha, corresponde a la primera, segunda, tercera, .. función de Fourier de un grafo. Por ejemplo, $\phi_1$ tiene ocilaciones con valores positivos (rojo) y negativos (azul), de igual manera, para $\phi2$, $\phi3$. Estas ocilaciones dependen de la topología del grafo, las cuales están relacionadas con la geometría de los grafos tales como comunidades, núcleos (hubs), etc, y es útil para agrupar grafos. Ver abajo.

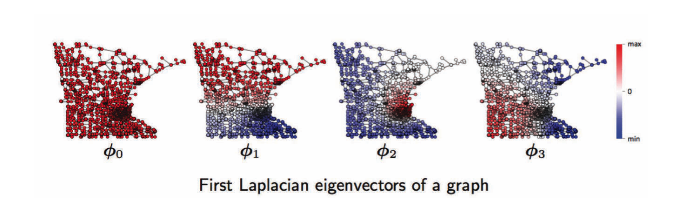
Fig. 17: Dominio de grafo: Funciones de Fourier en un grafo.

Paso 3. Transformada de Fourier

\[\begin{aligned} \underset{n \times 1} h &=\sum_{k=1}^{n} \underbrace{\left\langle\phi_{k}, h\right\rangle}_{\mathcal{F}(h)_{k}=\hat{h}_{k}=\phi_{k}^{T} h}\underset{n \times 1}{\phi_{k}} \\ &=\sum_{k=1}^{n} \hat{h}_{k} \phi_{k} \\ &=\underbrace{\Phi \hat{h}}_{ \mathcal{F}^{-1}(\hat{h}) } \end{aligned}\]

Series de Fourier: funciones de descomposición $h$ con funciones de Fourier.

Tomemos la función $h$, la cual, proyectada en cada función de Fourier $\phi_k$, resulta en el coeficiente de las series de Fourier de $k$, un escalar, y después se multiplica por la función $\phi_k$

La transformada de Fourier es básicamente proyectar a la función $h$ en las funciones de Fourier, y como resultado se obtienen los coeficientes de las series de Fourier.

Transformada de Fourier/ coeficientes de las series de Fourier

\[\begin{aligned} \underset{n \times 1}{\mathcal{F}(h)} &=\Phi^{T} h \\ &=\hat{h} \end{aligned}\]

** Inversa de la Transformada de Fourier**

\[\begin{aligned} \underset{n \times 1}{\mathcal{F}^{-1}(\hat{h})} &=\Phi \hat{h} \\ &=\Phi \Phi^{T} h=h \quad \text { as } \mathcal{F}^{-1} \circ \mathcal{F}=\Phi \Phi^{T}=\mathrm{I} \end{aligned}\]

Las transformadas de Fourier son operaciones lineales, las cuales multiplican a una matriz $\Phi^{T}$ por un vector $h$

Paso 4: Teorema de la Convolución

La transformada de Fourier de una convolución de dos funciones es el producto punto de sus transformadas de Fourier.

\[\begin{aligned} \underset{n \times 1} {w * h} &=\underbrace{\mathcal{F}^{-1}}_{\Phi}(\underbrace{\mathcal{F}(w)}_{\Phi^{T} w=\hat{w}} \odot \underbrace{\mathcal{F}(h)}_{\Phi^{T} h}) \\ &=\underset{n \times n}{\Phi}\left( \underset{n \times 1}{\hat{w}}\odot \underset{n \times 1}{\Phi^{T} h}\right) \\ &=\Phi\left(\underset{n \times n}{\hat{w}(\Lambda)} \underset{n \times 1}{\Phi^{T} h}\right) \\ &=\Phi \hat{w}(\Lambda) \Phi^{T} h \\ &=\hat{w}(\underbrace{\Phi \Lambda \Phi^{T}}_{\Delta}) h \\ &=\underset{n \times n}{\hat{w}(\Delta)} \underset{n \times1}h \\ & \end{aligned}\]

El ejemplo de arriba es la convolución de $w$ y $h$, ambos con dimensiones de $n \times 1$, esto equivale a la inversa de la transformada de Fourier del producto punto entre la transformada de Fourier de $w$ y $h$. La fórmula de arriba muestra que también es igual a la muliplicación de las matrices $\hat{w}(\Delta)$ y $h$.

La convolución de dos funciones en el grafo $h$ y $w$ consta de tomar la función espectral de $w$ y aplicarla a la Laplaciana y multiplicarla por $h$, y esta es la definición de una convolución del espectro. Sin embargo, la complejidad del cómputo es $\mathrm{O}\left(n^{2}\right)$, mientras que $n$ es el número de nodos en el grafo.

Limitaciones

La convolución espectral contra el dominio de grafos no es invariante de cambio, lo cual significa que si se realiza un desplazamiento, las dimensiones de la función también se modificarán, mientras que en el dominio de cuadrícula / euclideano, no.

Libro recomendado

Teoría de grafos espectrales, Fan Chung, (análisis armónico, teoría de grafos, problemas de combinatoria, optimización) Título original (en inglés): Spectral graph theory, Fan Chung.

---

📝 Bilal Munawar, Alexander Bienstock, Can Cui, Shaoling Chen
JonathanVSV
27 Apr 2020